凸多边形相似判定问题

唐乐红

(福州阳光学院， 福建福州 350015)

凸多边形相似判定问题

唐乐红

(福州阳光学院， 福建福州 350015)

本文通过利用已有的秘密判定相等协议、 集合相等判定协议、 数据对应成比例判定协议， 设计出凸多边形相似判定协议， 并分析了其正确性、 安全性和复杂性.

计算几何； 集合相等； 凸多边形； 相似判定

0 引言

如果一个多边形的所有边中， 任意一条边向两方无限延长成为一条直线时， 其他各边都在这条直线的同一侧， 那么我们就称这个多边形为凸多边形(边数大于3). 生活中常见的正多边形等都是凸多边形. 判定两个凸多边形是否相似， 在数学、 物理等学科上都有很多的实际应用.

本文假定双方的计算环境是安全的， 且前提 是双方都能严格遵守协议的规程. 在满足以上条件的情况下， 利用秘密判定相等协议、 集合相等判定协议、 数据对应成比例判定协议， 本文设计出凸多边形相似判定协议.

1 基础协议

1.1 秘密判定相等协议

两个用户希望在不向对方泄露自己数据信息的情况下， 比较出各自所持有数据是否相等. 如果双方数据不相等时， 则要求任何一方都不能够知道对方的数据. 这就是秘密判定问题[1].

1.2 集合相等判定协议

两个用户各自拥有一个集合， 如何在不泄露双方各自集合信息的情况下， 判定出两个集合是否相等[2]， 这就是集合相等判定问题. 协议具体如下：

输入： Alice拥有集合X={x1,…,xm},Bob拥有集合Y={y1,…,ym}.

输出： 谓词P(X,Y).

执行过程：

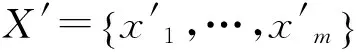
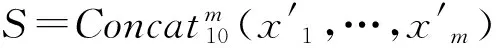
(3) Alice和Bob各自在本地利用商量好的散列函数， 计算出S′=hash(S)和T′=hash(T).

(4) Alice和Bob共同调用秘密判定相等协议判定S′与T′是否相等. 如果相等， 则返回结果为P(X,Y)=1； 否则P(X,Y)=0.

1.3 数据对应成比例判定协议

两个用户各自拥有一组数据， 如何在不向对方泄露自己数据的前提下， 秘密判断出两组数据是否对应成比例， 这就是数据对应成比例判定问题[3]. 协议具体如下.

输入： Alice拥有数据X=(x1,…,xn)， Bob拥有数据Y=(y1,…,yn).

输出：X与Y是否对应成比例.

执行过程：

(1) 对每一个i(i=1,…,n-1)， Alice和Bob完成以下任务：

①Alice和Bob各自在本地计算， 分别得到Xi=(xi,-xi+1)和Yi=(yi+1，yi).

②利用Xi和Yi， Alice和Bob共同执行点积协议， Alice得到ui=xiyi+1-xi+1yi+vi， 随机数vi则是由Bob选定的.

(2) Alice得到U=(u1，u2， …，un-1)， Bob得到V=(-2v1， -2v2， …， -2vn-1).

(4) Alice和Bob各自在本地计算， 分别得到

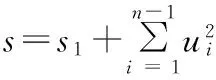
(5)利用s和t， Alice和Bob共同执行秘密判定相等协议. 如果相等， 则说明X与Y对应成比例； 否则说明X与Y不对应成比例.

2 凸多边形相似判定协议

2.1 问题描述

Alice拥有角数据为A=(α1,α2,…,αn)， 边数据为X=(x1,…,xn)的凸n边形； Bob拥有角数据为B=(β1,β2,…,βm)， 边数据为Y=(y1,…,ym)的凸m边形. 双方希望在不向对方透露自己数据的情况下， 合作判定出这两个凸多边形是否相似. 判定完成后， 双方只能知道两个凸多边形是否相似， 而不能从中得知对方的其他信息.

对于两个凸多边形， 如果能同时满足： ①角对应相等； ②边对应成比例， 则说明这两个凸多边形是相似的. 角对应相等且边对应相等的两个凸多边形， 我们称为全等凸多边形[4].

2.2 问题分析

首先， 我们对双方的角数据要按照从大到小(或从小到大)的顺序排列. 因为角要对应相等， 角度相同的角的个数必然一样. 因此， 双方的角数据先按照从大到小(或从小到大)的顺序排列， 然后利用集合相等判定协议进行判定. 如果不相等， 说明两个凸多边形肯定不相似. 如果相等， 再进行角对应相等判定.

角对应相等判定方法： 先找出凸多边形中角度最大的角(假设存在这么一个角)， 让其作为角数据中的第一个元素. 然后不按照时针方向， 而是按照向着邻近此角的两个角当中的较大角的方向， 对所有的角进行排列. 这样排列后， 就可以把角数据可能的对应方式找出来了， 所以只要进行一次角对应相等判定即可. 如果角对应相等判定不成立， 则两个凸多边形肯定不相似； 如果角对应相等判定成立， 则要继续判定边是否对应成比例.

边对应成比例判定方法： 我们可以利用前面角对应相等的信息， 对边也进行按角对应关系的顺序排列好. 把角对应信息应用到边对应上， 也就是把边的可能对应方式找出来. 这同样可以减少很多不必要的判断， 最后只需要进行一次边对应成比例判定就可以了. 如果边对应相等判定成立， 则说明两个凸多边形肯定相似， 否则说明两个凸多边形不相似.

2.3 协议描述

假设Alice和Bob的角数据是按从小到大的顺序排列好的. 通过上面的分析， 可以得到协议描述如下：

输入： Alice拥有一个凸n边形， 角数据为A=(α1,…,αn)， 边数据为X=(x1,…,xn). Bob拥有拥有一个凸m边形， 且角数据为B=(β1,…,βm)， 边数据为Y=(y1,…,ym).

输出： 两个凸多边形是否相似.

执行过程：

(1) Alice和Bob共同利用秘密判定相等协议，判定两个凸多边形的边数是否相等。如果相等，则协议继续。如果不相等，说明两个凸多边形不相似，协议结束。

(2) Alice和Bob共同利用集合相等判定协议，判定集合A,B是否相等。如果相等，则协议继续。如果不相等，说明两个凸多边形不相似，协议结束。

(3) Alice和Bob各自在本地找出角数据中角度不重复的最大角，然后以此角作为新的角数据中的第一个元素，并按照向着邻近此角的两个角当中较大的方向，对所有角进行重新排列，得到新的角数据A′和B′。

(4) Alice和Bob共同利用集合相等判定协议，判定集合A′和B′是否相等。如果相等，则协议继续。如果不相等，说明两个凸多边形不相似，协议结束。

(5) Alice和Bob各自在本地根据角数据的排列顺序，对边数据也按此顺序重新排列，得到新的边数据X′和Y′。

(6) Alice和Bob共同利用数据对应成比例判定协议判定X′,Y′是否对应成比例。如果对应成比例，则说明两个凸多边形相似，协议结束；如果不对应成比例，则说明两个凸多边形不相似，协议结束。

2.4 协议分析

正确性分析： 根据上面的分析以及协议的内容， 我们可以很容易看出， 两个边数相等的凸多边形， 只要角数据相等且边对应成比例， 则两个凸多边形必然相似的. 综上所述， 本协议是正确的.

复杂性分析： 本协议调用了1次秘密判定相等协议、 1次的数据对应成比例判定协议、 2次集合相等判定协议. 若所采用的秘密判定相等协议是基于可交换加密的， 则此协议的通信次数为3， 数据对应成比例判定协议的通信次数为3mn+2， 集合相等判定协议的通信次数为3， 所以本协议的通信次数为3+6+3mn+2. 本协议的计算代价主要为执行12次可交换加密方案中的加密运算， 以及4mn次同态加密方案中的加密运算和2mn次同态加密方案中的解密运算.

3 结语

网络的兴起， 使得隐私保护问题得到了越来越多的关注. 保护私有信息的计算几何问题在很多领域也得到了越来越广泛的应用. 利用已有的秘密判定相等协议、 集合相等判定协议以及数据对应成比例判定协议， 本文提出了凸多边形相似判定协议， 并对协议的正确性、 安全性和复杂性进行了分析.

[1] Du W,Atallah J.Privacy-preserving cooperative scientific computations[C].Nova ,Scotia Canada:The 14th IEEE Computer Security Workshop,2001:273-282.

[2] 李顺东,王道顺,戴一奇.两个集合相等的多方保密计算[J].中国科学，2009,39(3):305-310.

[3] 罗永龙,黄刘生,荆巍巍,等.空间几何对象相对位置判定中的私有信息保护[J].计算机研究与发展,2006,43(3):410-416．

[4] 王锵.一些基于私有信息保护的计算几何问题研究[D].兰州:兰州理工大学,2009.

Similarity Judgment Problem of Convex Polygons

TANG Le-hong

(Yango College, Fuzhou 350015, China)

Convex polygon, as a relatively common geometric figure, has a wide range of applications in daily life, and it has become a research direction in the Privacy-Preserving Computational Geometry (PPCG). In this paper, by using secret decision equality protocol, set equality decision protocol and proportional agreement protocol, we propose a protocol in similarity judgment problem of convex polygons. And furthermore analyze correctness, security and complexity.

computational geometry; set equality; convex polygon; similarity judgment

TP309

A

1009-4970(2017)11-0013-03

2017-04-09

唐乐红(1985—)， 女， 硕士， 讲师. 研究方向： 计算机科学与技术.

[责任编辑 胡廷峰]