三维边界元法计算变电站空间工频电场环境*

2017-12-21潘超谌骏哲刘士利

电测与仪表 2017年13期

潘超，谌骏哲，刘士利

（东北电力大学电气工程学院，吉林吉林132012）

0 引言

在电力工业不断完善的今天，大电容、大电流、大电网、高电压、远距离输电将成为电力系统发展的主要方向。高压输变电系统已获得普及，成为我国电力系统主干网络，特高压已经过设计论证并进入实施阶段。考虑到电磁环境相关指标的实际要求以及系统稳定有效的工作，对高压变电站电磁环境的探索是非常有意义的。国际上部分研究人员利用对变电站电场分布规律进行检验分析，表示主变、开关、断路装置及接线覆盖范围均属于强度明显的区间［1］，所以，有关特高压交流变电站具体规划与建设，首先需要了解变电站空间电场与设备附近电场分布的基本情况，如此才能使设计结果更加合理。

现阶段，计算变电站空间电场包含模拟电荷法［2-4］、矩量法［5］以及边界元法［6］。通过模拟电荷法对导线产生的电场进行处理，所得结果精确，只是在处理边界复杂环境时，这种方法必须多次确认模拟电荷有效位置与数量，流程繁琐，一旦无法确定电荷布置的有效点，这种方法将不具备任何价值。所以，部分专家采取这种方法对变电站空间电场进行求解，并未考虑设备带来的干扰，仅仅研究母线产生的电场，只是这类简化处理在研究设备附近电场情况时，结果存在明显的误差。变压器和电抗器周围设备比较多，除了有高低压引线以外，还有均压环等其它设备，在计算电场过程中，除了要考虑附近导线上的电荷以外，还必须考虑均压环等设备上的面电荷，所以，文章通过边界元法对变电站空间电场的计算进行分析。

文中主要工作是通过三维边界元法对荆门1 000 kV变电站设备附近电场进行模拟研究，基本包含各站的主变、高压并联电抗器、避雷器、接地开关、电容式电压互感器等附近相关设备。推导了三维空间合成电场极值的计算公式，并通过ANSYS仿真软件对其正确性进行了验证。

1 三维边界元计算空间电场

1.1 间接边界元方程

边界元法属于积分方法，可以有效处理边值情况，其原理便是把微分方程改变为边界积分方程，再将方程离散成代数方程组并求解计算。

假定空间区域V边界包含曲面S1与S2两部分，且电荷体密度 ρ（r′）。分别用r和r′表示场点和源点，R＝r-r′。如果边界条件与区域内电荷分布情况已知，对于区域中、边界处对应电位与电场强度情况，能够通过以下边值问题计算进行处理：

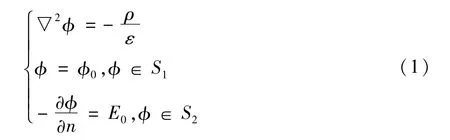
式中φ代表电位；ε代表区域内介质对应的介电常数；en代表边界外法线方位；φ0代表边界S1处电位；E0代表边界S2处法向电场强度。利用格林恒等式，上式化为：

式中r作为区域内的场点，一旦场点移动至边界处，式（2）则变成：

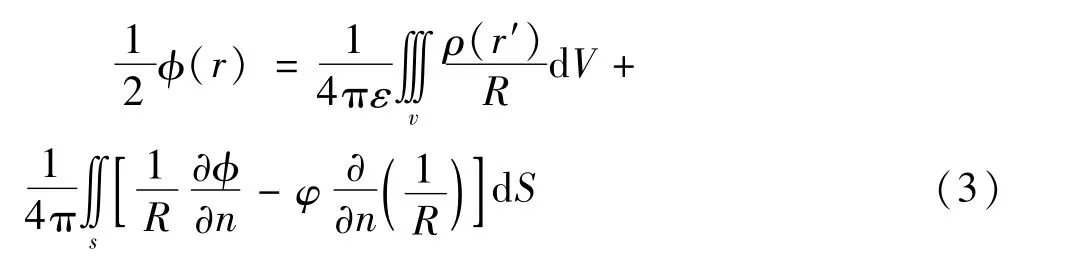
考虑区域内无体电荷分布的拉普拉斯情况，我们可以把式（3）改变成：

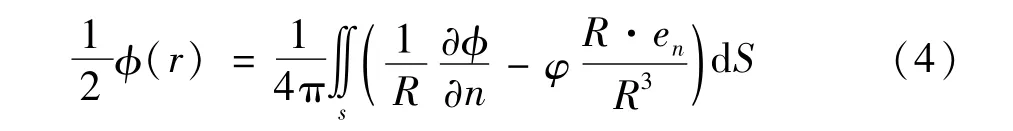
对边界进行离散，通过伽辽金加权余量方法进行处理，式（4）改变成：

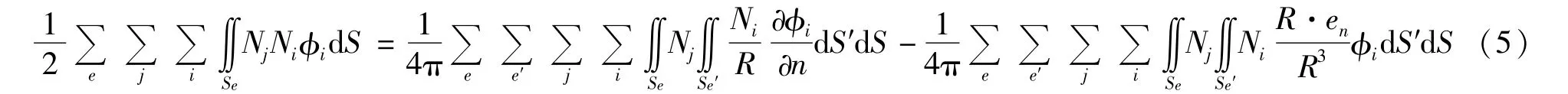
将式（5）写成矩阵的形式：

如果边界电位向量u确定，利用式（6）便能够计算出边界电场强度向量E，借此确定电荷面密度σ。同时，通过模拟电荷法可以得到导线上的电荷分布τ。

如果面、线两种电荷分布σ与τ确定，可根据电场积分公式计算场点对应电场强度：

式中σ为求解得到的电极面电荷密度；τ为导线上的电荷线密度；x′、y′、z′为源点坐标；x、y、z为所考虑平面上场点的坐标，对所有源单元求和，即可得到所有电荷在场点产生的电场。

1.2 基于边界元法的三维空间合成场强极值计算

基于三维边界元计算，对空间场域进行合成计算。假设在空间某点沿任意方向A有方向余弦cosα、cosβ、cosγ，EXR、EYR、EZR及EXI、EYI、EZI分别为电场强度有效值三个分量的实部和虚部，则A方向上的场强有效值EA的平方为：

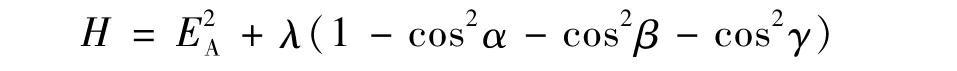
令：cosα＝u，cosβ＝v，cosγ＝ω；

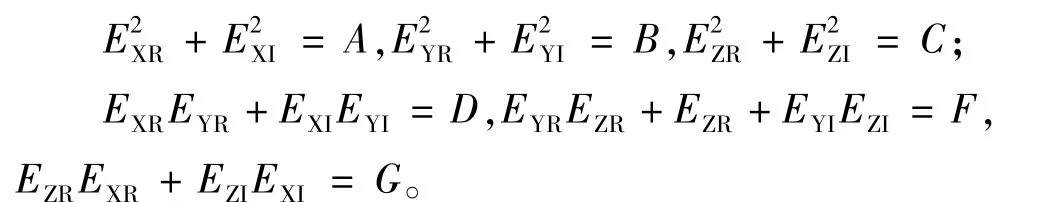
根据拉格朗日乘数法，目标函数H有极值的必要条件是：

由于场强一定存在极值，所以式（10）存在非0解，那么其系数行列式同样是0：

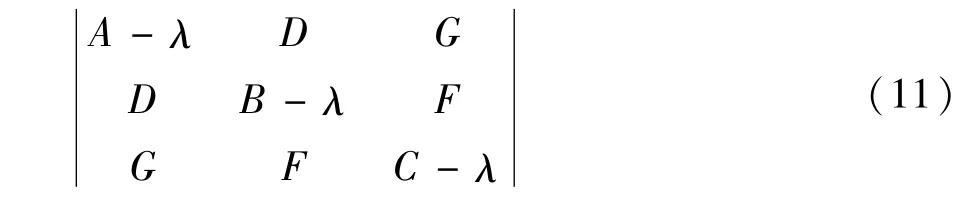
2 仿真计算

2.1 计算模型

荆门1 000 kV变电站主变及附近设备的计算模型如图1所示。

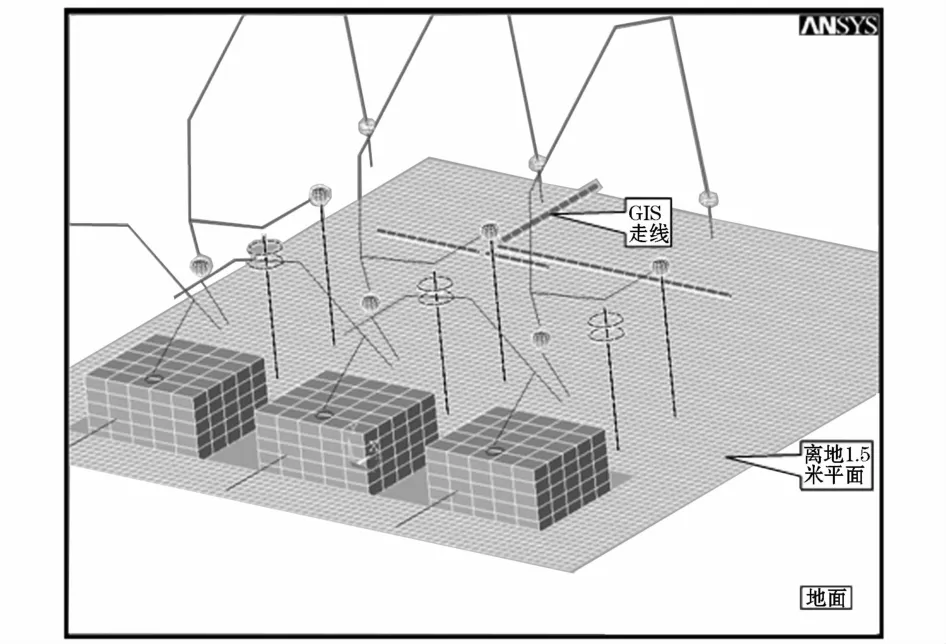
图1 主变及附近设备计算模型示意图Fig.1 Schematic diagram of calculation models for main transformers and other equipments

图1～图2表示的模型中，除了GIS走线以外，A、B、C三相的其它设备完全对称，下面以B相为例进行研究，如图3所示。

图3中方形体B表示B相变压器接地外壳，①表示110 kV引线；②表示500 kV均压环；③表示500 kV引线；④表示1 000 kV引线；⑤表示电容式电压互感器对应均压环；⑥表示氧化锌避雷器对应均压环；⑦表示变压器1 000 kV出线端的四个均压环；⑧表示1 000 kV引线到GIS套管处的两个均压环。各模型的参数如表1所示。

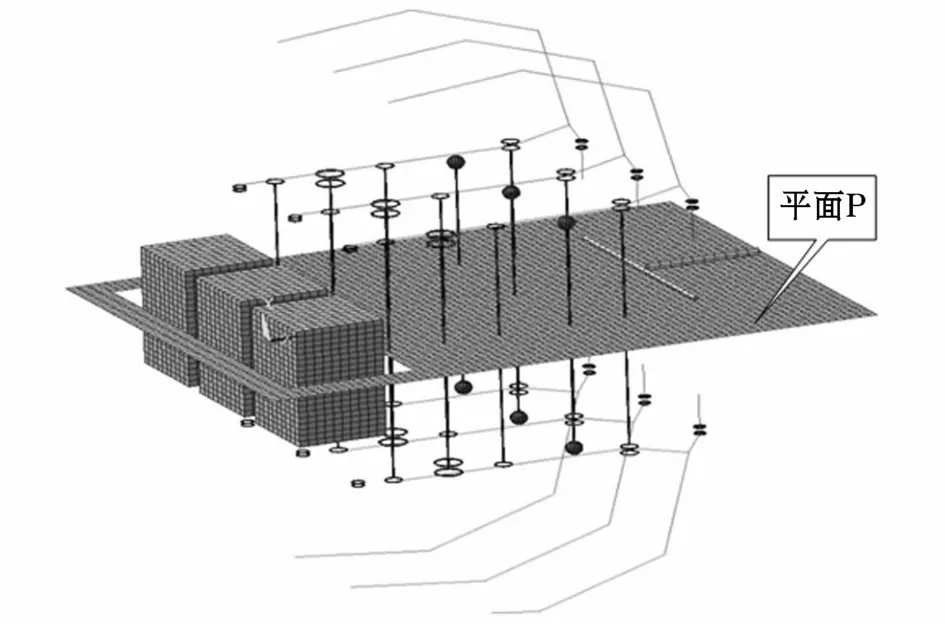
图2 电抗器及附近设备镜像模型Fig.2 Image models for reactors and near equipment

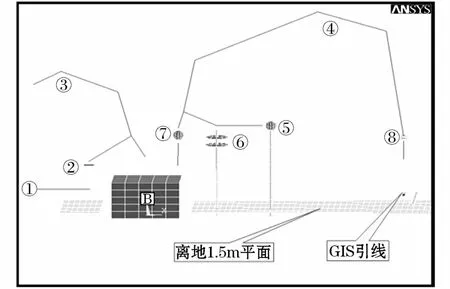
图3 B相主变及附近设备计算模型示意图Fig.3 Schematic diagram of calculation models forB-phasemain transformers and other equipments

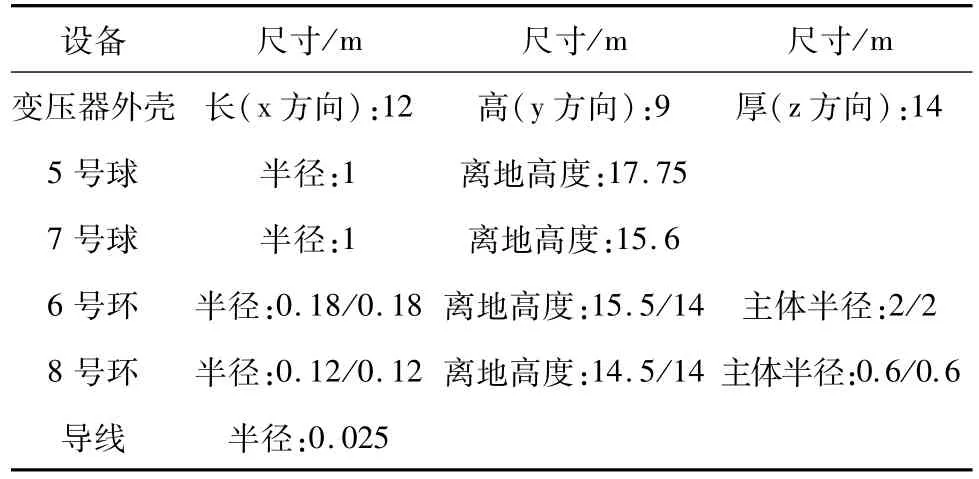
表1 模型参数Tab.1 Parameters of models

2.2 结果分析

编写边界元程序，根据B相设备参数进行计算，施加边界条件为相电压有效值，按式（9）～式（11），计算离地1.5 m（约为人体心脏处）平面上电场强度有效值的最大值，约为14.16 kV／m。

利用ANSYS软件进行仿真，根据设备参数建模，计算主变附近电场强度分布，场强有效值的最大值云图见图4。

图4 主变附近场强有效值的最大值分布云图Fig.4 Maximum value cloud image of electric field around the main transformer field around the reactors

平面P上电场强度最大值分布见图5所示，可以看出，在A、C相对称的位置即边相位置上出现了场强比较大的区域，这和传统方法的结论是一致的，该区域分别偏离A、C相电抗器轴线2 m左右。电场强度的最大值出现在C电容式电压互感器的下方区域，最大值为9.178 kV／m。

图5 电抗器附近场强最大值云图Fig.5 Maximum value cloud image of electric

为了验证本文所采用方法的准确性，在距设备约20 m处的虚拟走廊L上进行现场测量，如图5所示，该直线上电场强度最大值的仿真计算结果与实际两侧数据对比如图6所示。

由图5可以看出，A、C两个虚拟走廊L处出现两个最大值，B相对应最小值，测量曲线和仿真曲线对比结果基本吻合，变电站工频电场最大值出现区域的曲线基本一致，是重点研究的位置。B相由于处于中间位置，周围设备较多，测量时受到的影响较大，因此，曲线在最小值部分稍微有些偏差。由于仿真模型的简化，和实际变电站分布的不同都是造成结果误差的原因。通过结果对比表明，本文方法能够有效准确地模拟实际变电站空间电场分布情况，从而为后续的电场强度曝露限值安全评估奠定基础。