双主电源并联运行的微电网小信号稳定性分析与控制参数优化*

2017-12-21黄素娟窦晓波焦阳杨野青

电测与仪表 2017年13期

黄素娟，窦晓波，焦阳，杨野青

（1.国电南瑞科技股份有限公司，南京211106；2.东南大学电气工程学院，南京210096）

0 引言

进入21世纪以来，以实现可持续发展为目标，新能源技术成为了研究热点。其中，微电网技术不仅可以平抑分布式电源对大电网的不利影响，而且能够最大限度发挥分布式电源灵活、易控制的优势，尤其在海岛、山区等实现电网供电成本过高的地区，采用独立式微电网供电成为了最具经济性的选择。

然而，使用不同的控制方式，会对离网独立运行微电网的运行产生负面的影响，目前应用较多的控制方法有下垂控制、单主从控制和多主从控制。文献［1-4］分析了在下垂控制方式下功率均分特性、电压频率稳定性互为矛盾；在孤岛运行的微电网中，主从控制系统应用更多。对于主从控制策略，又分为单主从和多主从两种电源控制模式［5］，即系统中一个或多个电源作为主电源，使用V／f控制时，用于提供电压和频率支撑，其余电源作为从电源，采用PQ控制时，则提供恒定功率输出。其中单主从电源控制依赖一个主模块，可靠性不高，多主从控制相对单主从控制具有多个主电源，因此可靠性高。

由于微电网中多数电源采用电力电子接口，系统的惯性较小，在受到干扰时容易发生失稳，因此系统的稳定性也是微电网技术中最令人关注的问题之一。微电网系统能够持续稳定运行的前提是具有小信号稳定性［6-8］。在特定的控制方式下，微电网的小信号稳定性受哪些参数影响，其受到干扰时的动态过程特点如何均需要通过系统的小信号模型来分析。目前已有文献做了相关研究：文献［8］建立了分布式电源的微网小信号模型，包含了两台分布式电源，并通过特征值分析，找出了影响主低频特征值的状态变量；文献［9］详细推导了基于固态变压器的环形微网的小信号模型，并通过特征值分析选择了下垂系数；文献［10］所建立的微网小信号模型包含了直流侧模型的光伏和储能，并总结了系统遭受扰动时的振荡模式，具体为三种不同频率的震荡模式。

考虑到多主并联运行时的情况，逆变器并联运行时需要对相互之间的环流进行抑制，因此控制系统更为复杂。文中以含有两台主电源的孤岛微电网系统为研究对象，采用多主从控制方式通过建立系统的完整小信号模型，分析系统的稳定性，并根据特征根的参与因子，确定了影响系统主特征根的状态变量。由于多主电源并联系统控制较为复杂，控制器能否选取到合适的控制参数将直接影响系统的动态性能和稳定性，因此文章在对系统进行小信号稳定性分析的基础上，提出了基于小信号模型的控制参数综合优化方案，将根轨迹法与粒子群算法相结合，以增大系统阻尼为原则，对系统的控制参数进行了协调优化，以提升系统的动态性能。

1 基于环流抑制的双主电源并联运行控制方法

对于多主电源并联系统，元件参数的差异会导致主电源之间会产生环流。因此，多主从控制需要对主电源之间的环流进行抑制。对于主电源之间的环流抑制方式，已有大量文献进行了研究［11-17］。但存在输出外特性软、动态效果欠佳等问题。文章在总结以上文献研究成果的基础上，以双主电源并联系统为分析对象，采用功率环控制器抑制环流，在传统双环控制之前增加功率环，对两台主电源均分输出功率，以达到抑制环流的效果。系统的基本结构如图1所示。

其中MGCC为微电网中央控制器，通过收集各台逆变器的输出功率数据，对功率进行均分处理并将指令发送给各台逆变器的控制器。控制器根据指令对本台逆变器微调，系统等效电路如图2所示。

图1 微电网结构Fig.1 Structure of micro-grid

图2 系统等效电路Fig.2 System equivalent circuit

其中V0乙φ0为母线电压，Vi乙φi、Pi、Qi分别为第i台逆变器输出的电压、有功功率和无功功率，Rlinei、Xlinei为第i台逆变器与母线之间的连接线阻抗，Rload、Xload分别为等效的有功和无功负载（i＝1，2）。

定义ΔV＝V1-V2，Δφ＝φ1-φ2，两台逆变器输出的有功功率差ΔP＝P1-P2，无功功率差ΔQ＝Q1-Q2，设Rline1＝Rline2＝R，Xline1＝Xline2＝X，每台逆变器的有功功率和无功功率调节量分别为PH、QH，则有［11］：

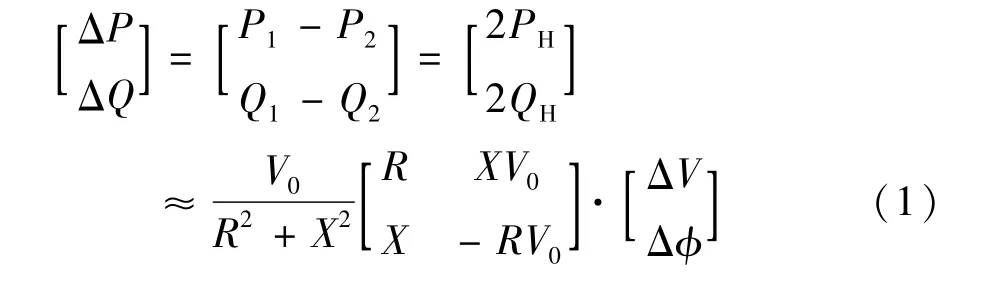
由式（1）可以看出，R与X共同影响有功和无功环流，在低压微电网中，R／X的值较大［18］，有功环流对幅值差比较敏感，无功环流对相角差比较敏感。因此两台逆变器的系统通过调节其幅值和相位消除环流的控制原理图如图3所示。

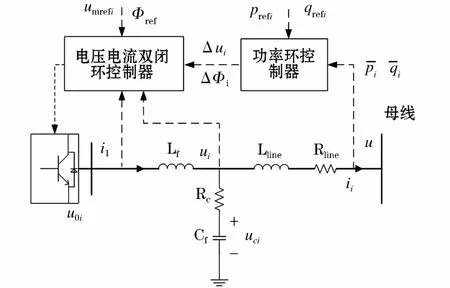
图3 逆变器控制原理图Fig.3 Inverter control schematics

由于逆变器并联系统中环流产生的根本原因是输出电压幅值和相位不同［14］，因此在文中，为了模拟实际逆变器由于各种因素造成的输出电压不相等的情况，将两台逆变器输出电压的幅值相位初始输入量umref1与umref2、φref1与 φref2设为不同的值，以模拟实际系统中的环流产生过程。

2 双主电源并联运行的微电网小信号建模

2.1 逆变器模块模型

逆变器模块的控制策略如图3示。其中滤波器为LC滤波器，Lf、Cf为滤波器的滤波电感和滤波电容，Rc为与滤波电容串联的电阻。设计功率环控制器如图4所示。

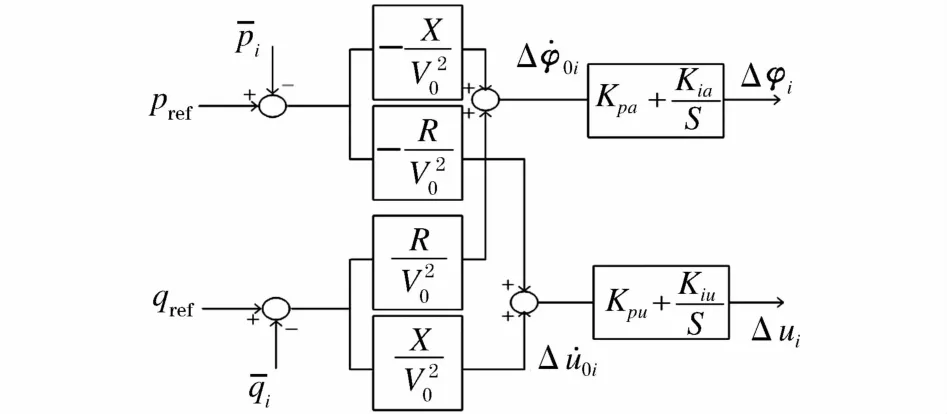
图4 功率环控制器框图Fig.4 The controller block diagram of power loop

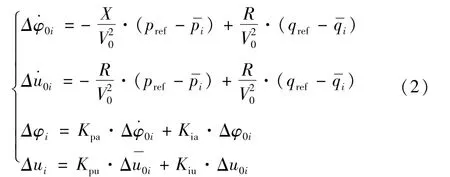
其中Pref、Qref为输出功率的目标值，本例中有将Pref、Qref代入式（2）中，当i分别取1和2时，方程组是线性相关的，即可得式（3）。

当系统中有多台电源且需要输出的功率各不相同时，为了便于分析，避免系统出现零特征值，文中将直接利用式（3）计算 Δφ2、Δu2：

电压电流双环控制框图如图5所示，其中电流环采用电感电流作为负反馈。

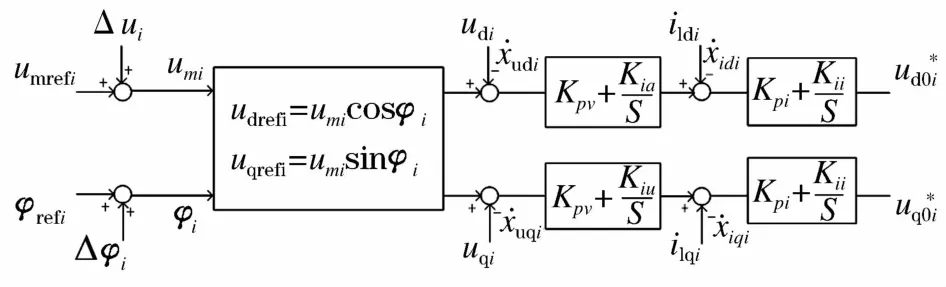
图5 电压电流双闭环控制框图Fig.5 Voltage and current double closed-loop control block diagram

式中 ωn为dq0坐标系的旋转频率；udi、uqi为滤波的输出电压；ucdi、ucqi为滤波电容上的电压；ildi、ilqi为滤波电感电流；Rline、Lline为线路模拟电阻、电感值；idi、iqi为逆变器输出端电流；ud、uq为母线电压的 d、q轴分量。

2.2 网络及全系统模型

由图3可以得到节点电压方程，结合式（2）～式（4）可得到全系统的完整数学模型，选取：

其中u＝［umref1，umref2，φref1，φref2］T为全系统建模的输入矩阵，将节点电压方程式在系统的稳态运行点处进行泰勒展开，只保留展开方程的一阶项，可得到全系统的小信号模型为：

式中A矩阵即为系统的状态矩阵。

3 系统小干扰稳定性分析

系统中两台并联电源额定功率均为50 kVA，母线额定电压220 V，额定频率50 Hz。其余参数如表1所示。

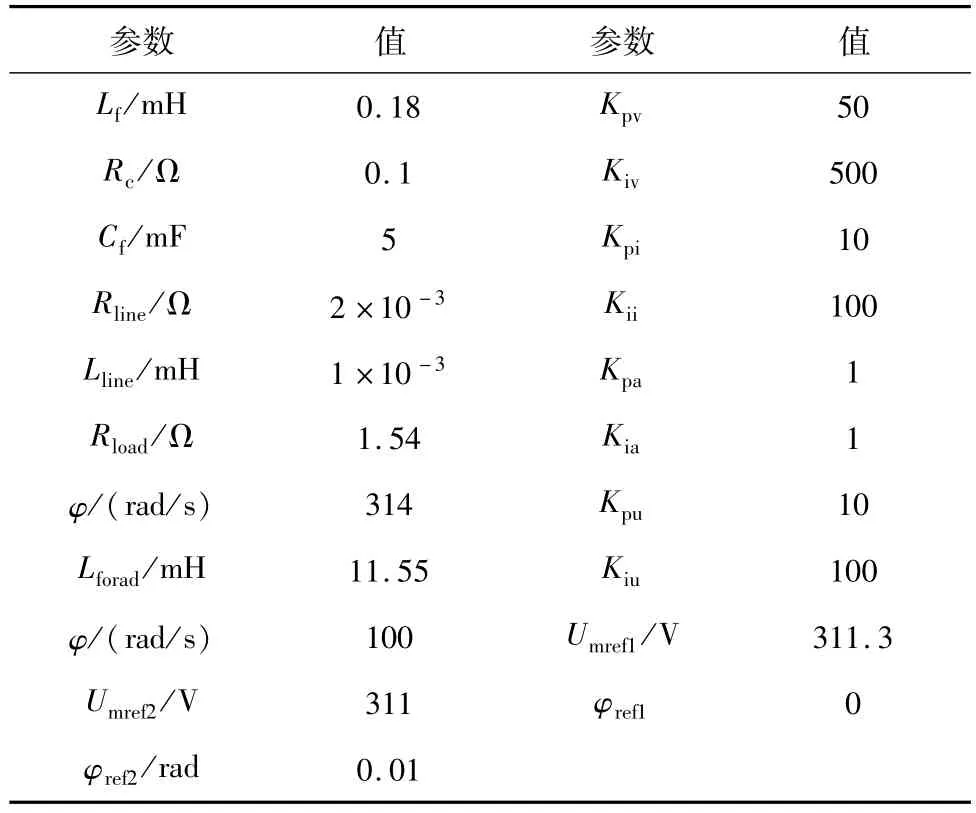
表1 系统参数Tab.1 System parameters

结合表1利用仿真软件计算得到系统稳态运行点处的参数值，求得A矩阵的特征值，其在复平面上的分布如图6所示。

根据李雅普诺夫稳定性理论，图中系统所有特征值均具有负实部，系统是稳定的。另外，特征值的虚部较为集中，高频振荡特征值虚部集中在314左右，相当于50 Hz上下。图中圈出的特征值距离虚轴较近，动态过程持续时间长，对系统稳定性影响最大，为系统的主特征值。主特征值共有6个，如表2所示。

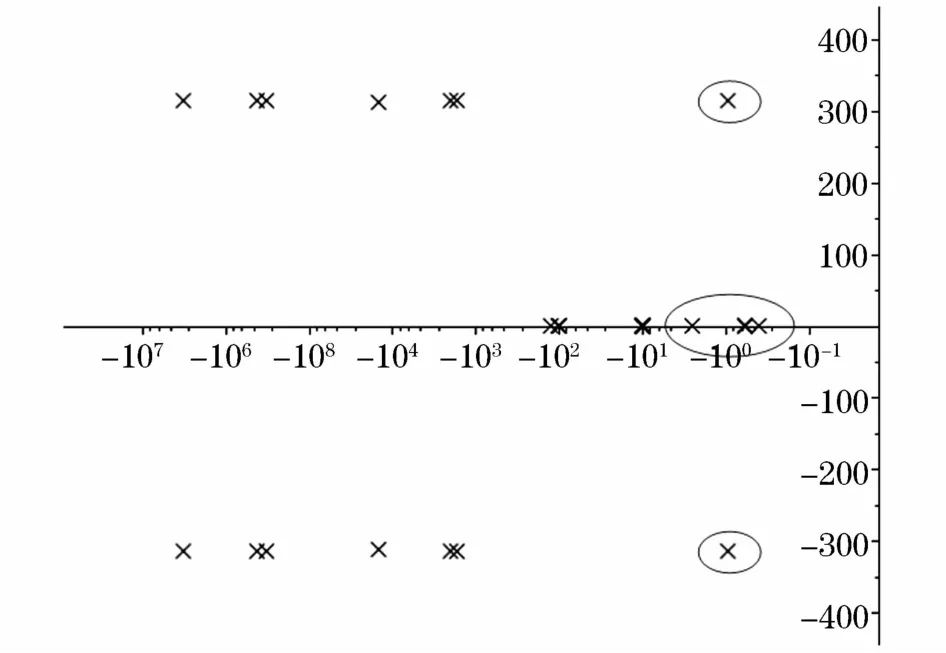
图6 系统特征值分布Fig.6 System eigenvalues distribution

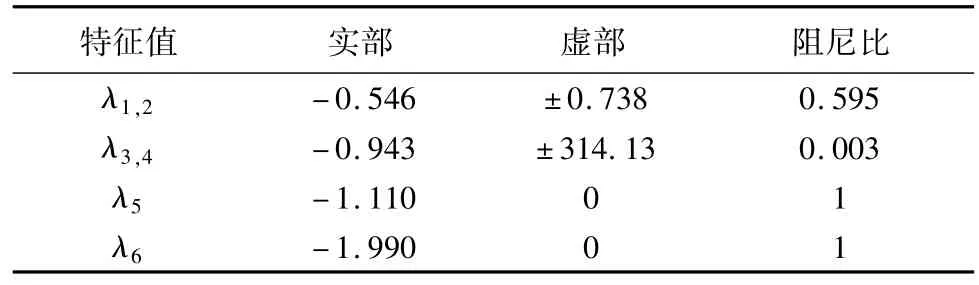
表2 系统主特征值Tab.2 System main eigenvalues

参与因子pki表示特征值小对状态矩阵对角元素akk的灵敏度，其值为左特征向量元素与右特征向量元素的φki乘积，即：

参与因子pki表示第i个特征值中第k个状态变量的参与程度，可以作为状态变量对特征值影响的一种度量。

对主特征值进行参与因子分析，得出结论：λ1，2主要与 Δu01、Xud1、Xud2有关；λ3，4主要与iloadld、iloadlq有关，因此 λ3，4主要受无功负载和母线电压影响；λ5、λ6则与 Δφ01、Xuq1、Xuq2有关。

由以上分析可以看出，系统是稳定的，但是所有的主特征值都靠近虚轴，意味着系统抗干扰性能不佳，受扰动时动态恢复时间长，且λ3，4的阻尼比过小，不利于系统稳定。因此下文中利用根轨迹法与粒子群算法相结合的算法对控制参数协调优化，使系统的主特征值远离虚轴，以改善系统的稳定性。

4 系统控制参数选取方案

4.1 基本优化方案

在每台逆变器中，均有三个控制器，电流环、电压环和功率环，每个控制器都采用PI控制，因此包括控制器参数全系统需要确定8个控制参数。粒子群算法适用于寻找最优解问题，这里将用于寻找一组最优控制器参数。粒子群算法中，合适的初始值可以极大提高运算效率，也能避免算法陷入局部最优解，因此，本文首先利用传统根轨迹法选取一组参数作为起点，同时确定每个参数的取值范围，再利用粒子群算法对控制参数进行协调优化，最终得到最优控制器参数。

4.2 基于特征值法的初步优化

文中需要优化的参数为Kpv、Kiv、Kpi、Kii、Kpa、Kpu、Kia、Kiu共八个控制参数，固定其中 7个参数，使一个参数在一定范围内变化时，系统特征值会发生改变，，变化规律会形成一个轨迹，即是系统的根轨迹。根据根轨迹变化趋势，可以选择一个合适的值作为初始值，这里合适指的是可以使系统的主特征值远离虚轴，增加系统抗干扰能力。

图7 Kpv变化时系统根轨迹Fig.7 System root locus when Kpv varies

首先令Kpv在［1，100］的范围内变化，绘出系统的根轨迹，结果如图7所示，图7（b）为图7（a）中圆圈内的放大图。由根轨迹可以看出，随着Kpv的增大，λ3，4逐渐靠近虚轴，并且有一对原本距离虚轴较远的特征值也迅速靠近虚轴。λ1，2变化不大，λ5、λ6则有靠近虚轴的趋势。

由于λ3，4对应高频振荡且阻尼比较小，因此在选取初始值的时候，应首先考虑增大其阻尼比，且使得其他主特征值远离虚轴。根据所绘制根轨迹图，确定Kpv初步优化的值为10，取值范围为［1，80］。

利用上述确定Kpv的优化方案，得到其余参数与取值范围如表3所示。

表3 初步优化的结果Tab.3 Preliminary results of optimization

这样便得到了采用根轨迹法初步优化的结果，由于优化过程还没有严谨的方法，因此控制器参数的精度不是很高，因此下一阶段将利用粒子群算法进行进一步优化，提高系统动态性能和抗干扰能力。

4.3 基于粒子群算法的进阶优化

文中，每个粒子均为一个八维向量，其所在位置代表八个控制参数的一组取值。在粒子群算法中，若各个粒子的初始位置随机确定，往往容易使算法陷入局部最优解［19］。因此本文利用上一节中根轨迹法得到的控制参数作为一个粒子的初始位置，以避免算法陷入局部最优解。

由初步优化得到的参数取值范围，可以确定粒子群算法的搜索空间。按照Kpv、Kiv、Kpi、Kii、Kpa、Kpu、Kia、Kiu的顺序，确定八维搜索空间第一维到第八维分别为［1，80］、［100，1 000］、［1，100］、［100，1 000］、［0.1，10］、［1，1 000］、［0.8，2］、［1，2 000］。

初始化各粒子的位置向量xni＝（）和速度向量，取上一小节根轨迹法得到的控制器参数，其余粒子在搜索空间内随机分布，vni在［-Vm，+Vm］范围内随机选取。

在粒子群算法中，通过“适应度”的概念判断一个粒子所在位置是否优劣，本文最终目标是增大系统阻尼，从而使系统主特征值远离虚轴，进而改善系统动态性能，因此设定粒子的适应度函数为：

式中p为适应度，σ1～σ6为系统所有特征值中离虚轴最近的六个特征值的实部，且σ1≥σ2≥σ3≥σ4≥…σ8，7-i为 σi的权值，σi离虚轴越近，权值越大。优化目标为使p最小。

计算每个粒子的适应度，将各个粒子的位置和适应度储存在pbesti中，将所有粒子中适应度最好的粒子位置和适应度储存在gbest中。

用式（9）更新粒子的速度和位置，即：

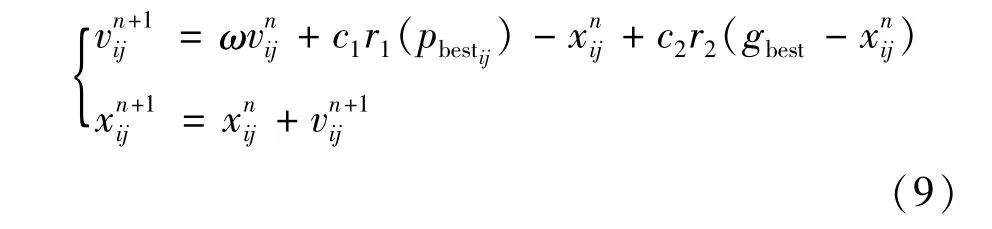
计算更新各粒子的适应度，若为最优值则取代之前的pbesti，否则舍弃，最终将该最优粒子和适应度储存在gbest中。返回式（9）继续计算，直至最大迭代次数。

文中设定，ω＝0.729 8，c1＝c2＝1.494 45，粒子个数d＝50，最大速度Vm＝5，迭代次数600。优化后的参数如表4所示。

表4 优化后的控制参数Tab.4 Optimized control parameters

图8为系统优化前与优化后的根轨迹对比图，由图可见，优化后系统的主特征值均有不同程度的左移。

图8 优化前与优化后主特征值对比图Fig.8 Eigenvalues comparison chart before and after optimization

5 仿真与实验验证

5.1 仿真验证

为了验证系统的均流效果与控制参数优化效果，设计了基于Simulink的仿真平台进行了时域仿真验证。系统拓扑与图2相同，系统参数与表1一致。

5.2 仿真结果分析

为了验证功率环对环流的抑制效果，令两台逆变器首先在电压电流双闭环控制下运行，达到稳态后加入功率环，如图9，图10所示观察两台逆变器输出功率的变化情况，控制参数与表4一致。

图9 加入功率环前后两台逆变器输出的有功功率Fig.9 Output active power of two inverters before and after power loop added

图10 加入功率环前后两台逆变器输出的无功功率Fig.10 Output active power of two inverters before and after power loop added

由图9、图10可以看出，在t＝6 s之前，系统中没有加入功率环，两台逆变器由于输出电压的幅值和相角存在差异，输出的有功和无功功率相差很大，说明相互之间存在很大的环流。t＝6 s时，加入了功率环的控制作用，两台逆变器的输出电压被矫正，输出功率经历一个动态过程之后收敛，说明功率环对环流有较强的抑制作用。

在此基础上，对控制参数的优化效果进行验证。将负荷突增一倍作为扰动，系统控制参数去三组，第一组是未优化的，第二组是根轨迹优化的，第三组是粒子群优化之后的。观察两台逆变器的输出功率的波动情况。

如图11、图12所示，第二台逆变器的输出有功／无功功率与第一台结果相似，由仿真结果可以看出，优化之前，遭受扰动需要4 s左右才能恢复稳态，优化之后，动态过程只需要不足1 s，动态过程时间大幅减少，验证系统动态性能得到显著提升。

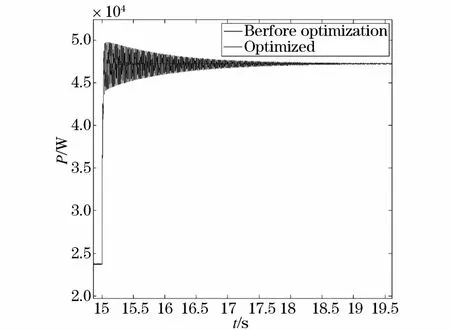
图11 P1优化前与优化后对比图Fig.11 Compared before and after optimization about P1

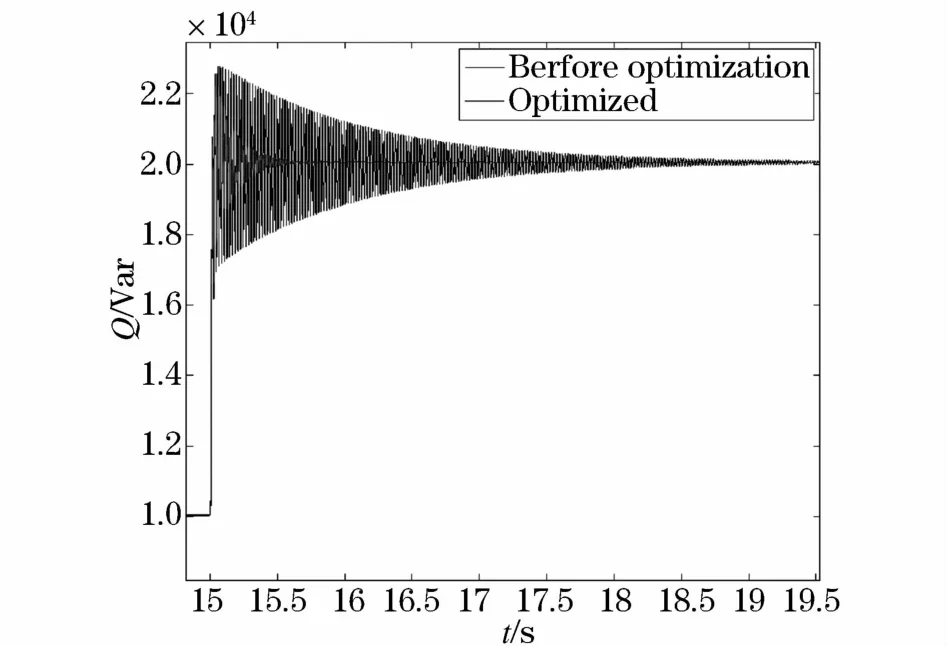
图12 Q1优化前与优化后对比图Fig.12 Compared before and after optimization about Q1

5.3 实验验证

5.3.1 实验平台

为了验证最终选取出的控制参数的实际控制效果，搭建了基于RTDS的半仿真实验平台。系统拓扑与图1相同，逆变器直流侧接储能，提供稳定直流电压，单个模块输出功率为50 kVA，母线额定电压220 V，额定频率50 Hz，系统结构与前文一致，系统参数见表1。在触发时刻（0ms）处负荷突增100%作为扰动，使用录波器记录两台逆变器输出的有功无功功率的波动情况。

5.3.2 实验结果分析

由图13、图14可见，在切除负荷时，两台逆变器的输出功率均迅速归零，且整个过程中两台逆变器的输出功率基本一致，没有发生剧烈波动或失稳，系统具有良好的稳定性，表明最终选取的控制参数具有很好的控制效果。