电力变压器有源降噪系统次级声源优化布放*
2017-12-21王国栋应黎明刘洋王晋伟杨鹏王东晖
王国栋,应黎明,刘洋,王晋伟,杨鹏,王东晖
(1.武汉大学 电气工程学院,武汉430072;2.国网湖北省电力公司检修公司,武汉430050)
0 引 言
随着我国经济的发展和用电需求的增加,大容量电力变压器深入负荷中心,导致变电站附近噪声强度增加,严重影响周边居民的正常生活[1]。电力系统和变压器制造业有必要采取科学合理的措施,控制变压器特别是室外变压器的噪声[2-5]。
电力变压器的噪声包括辅助冷却装置噪声和电力变压器本体噪声,噪声频率主要包括100 Hz、200 Hz、300 Hz、400 Hz、500 Hz和 600 Hz,为低频噪声。变压器噪声的低频特性使得传统的被动降噪技术效果不明显而且价格昂贵[6]。近二十年来,有源噪声控制(Active Noise Control,ANC)技术得到了广泛的研究,为变压器噪声控制提供了一个新的解决办法,其基本原理是利用次级声源产生和原有噪声频率相同、振幅相近、相位相反的声波,使之与原有噪声相互叠加,以达到降低空间噪声的目的[7]。与传统的无源技术相比,有源噪声控制技术特别适合控制低频噪声[8]。有源噪声控制系统主要分为控制器和电声两部分。电声部分用于确定次级声源的数目和在声场中的位置(称为布放问题)。次级声源的布放不仅影响整个控制系统的稳定性,而且影响噪声的控制效果[9]。因此,通过选择合适的次级声源数量及位置来最大限度地提高降噪量是有源降噪系统实用开发中需要解决的核心问题之一。
在实际工程应用中,往往是部分区域(比如变电站附近的居民楼)有降噪的需求,对此文献[10]提出用阵列式次级源来对噪声进行有源控制以达到局部空间降噪的目的,并且进行了初步的理论与实验研究。文献[11]研究了次级声源位置和声强度对有源降噪系统降噪效果的影响,并验证了一组典型优化方案的降噪效果。文献[12]由声场辐射模型推导出最优次级源强度,理论分析了次级源强度与次级源间距、次级源与噪声源距离、次级声源阵列的数目对降噪效果的影响。文献[13]针对封闭空间声场,建立了结构—声耦合场模型,采用正交试验法分析了次级声源强度与布放位置的综合作用对有源噪声控制系统降噪效果的影响。文献[14]建立了封闭空间的有源噪声控制模型,采用模拟退火法优化次级声源位置,在误差传感器处最多达到了0.5 dB的降噪量。文献[15]针对位置和次级声源强度的交互影响关系,提出了对固定参数和灵活参数进行交替优选,采用遗传算法进行渐次搜索的优化策略。虽然国内外正在开展变压器有源噪声控制的研究,但目前尚无成功应用的案例。
已有的次级声源优化布放的研究中,没有考虑变压器实际的声场环境,没有针对变压器降噪应用提出简洁有效的优化布放策略。文章参考已有研究成果,针对变压器有源噪声控制应用环境,结合声学理论提出了半自由空间的声场辐射模型,综合运用解析法和遗传算法优化不同数目次级声源的布放参数(位置和声源强度),仿真和实验验证了布放方案的有效性。
1 变压器噪声声场辐射模型
1.1 初、次级声源模型
考虑到电力变压器主要通过壳体表面向外辐射噪声,且变压器的几何尺寸与声波的半波长接近,可以将变压器简化等效成脉动球形声源模型[16],忽略简谐时间因子ejωt后,其辐射声压表达式为:
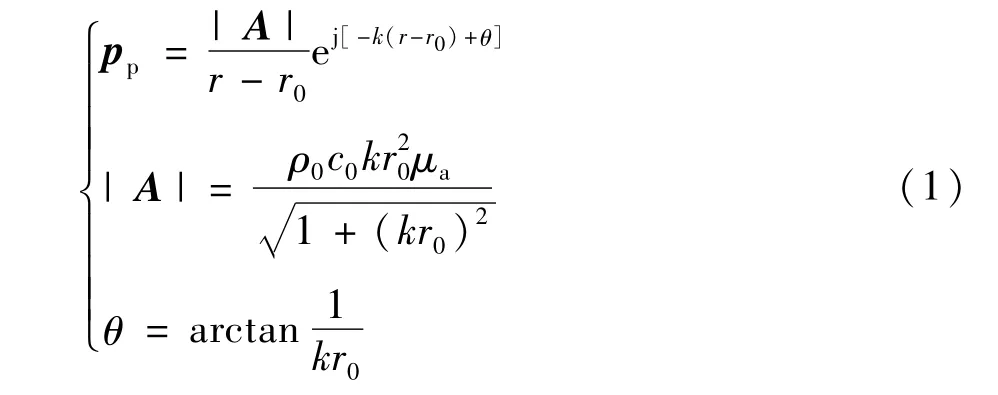

式中 ps为次级声源在观测点处的声压;r为次级声源到观测点的距离;qs为次级声源的声源强度。
1.2 半自由空间声场辐射原理
如果某空间声场存在地面为反射面,其余方向均符合自由空间声场的条件,则称其为半自由空间声场。半自由空间声场是一种更贴合变压器实际的声场环境。由镜像原理可知,半自由空间声场中脉动球源的辐射声场可以等效为是其本身与“镜像”虚源叠加产生的合成声场[17],如图1所示。
式中pp为初级声源在观测点处的声压;r为观测点到球源中心的距离;r0为球源半径;A为复数,|A|为其幅值;θ为A相角;ρ0为空气密度;c0为声波在空气中的传播速度;μa为球源的振动速度幅值;k为波数且k=ω/c0。
此外,变压器有源噪声控制系统通常采用扬声器阵列作为次级声源,扬声器的几何尺寸相对声波的半波长可以忽略,因此可以将次级声源近似等效为点声源模型,相应的声压辐射表达式为:
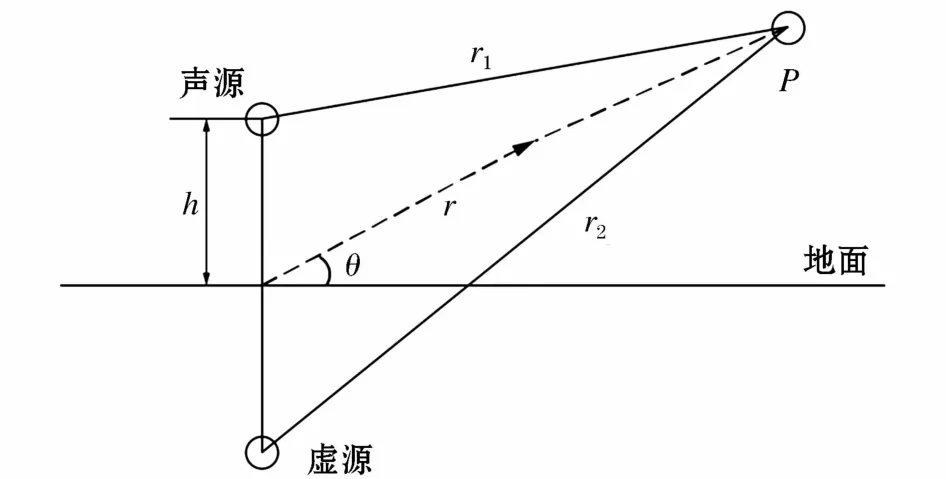
图1 半自由空间声场中点声源的辐射声场Fig.1 Acoustic radiation model of point sound source in half free space
半自由空间声场中点声源在观测点P处的声压为:
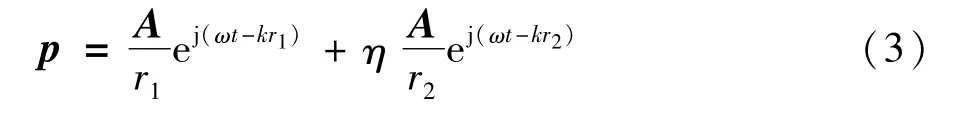
式中r1、r2分别为声源、虚源到观测点的距离;η为刚性壁面的声反射系数[18]。
1.3 变压器有源降噪系统声场辐射模型
假设半自由空间声场中有一电力变压器作为初级噪声源。变压器前方有由N个扬声器组成的次级声源阵列,选取远场中与次级声源阵列平行的平面为待消声面。根据声波叠加原理,可得待消声面任意观测点a处的声压pa为:

式中pa为初级声源在观测点a处的声压;qs为次级声源阵列强度,qs=(qs1,qs2,…,qsN)T;Zr为 1×N阶向量,是次级声源阵列及其“镜像”到a点的总的声传播阻抗,即由次级声源与其“镜像”的声传播阻抗矩阵相加得到,Zr=(Zr1,Zr2,…,ZrN),其任一元素可表示为:
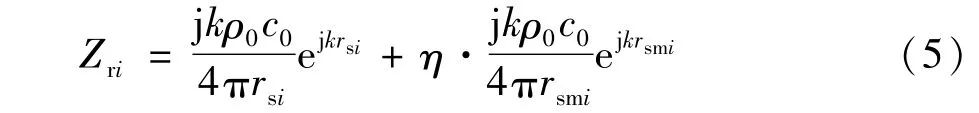
式中rsi、rsmi分别为声源阵列中第i(i=1,2,…,N)个次级源及其“镜像”到待消声面观测点a的距离;η为地面的声反射系数。
若在待消声面选取M个观测点,可得M个观测点处的声压表达式为:

式中 PM为M个观测点处的声压向量,PM=(pM1,pM2,…,pMM)T;Pp为初级噪声源在M个观测点处的声压向量,Pp=(Pp1,Pp2,…,PpM)T;ZMr为M×N阶矩阵;表示次级声源阵列到M个观测点的声传播阻抗矩阵。其任一元素可表示为:
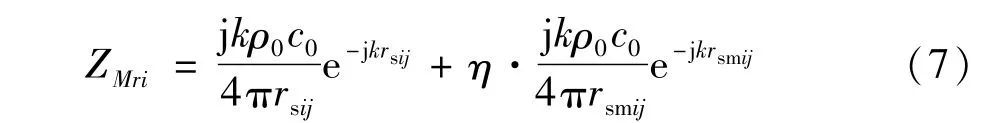
式中rsij、rsmij分别为第i个次级源及其镜像到第j(j=1,2,…M)个观测点之间的距离。
将M个观测点处声压的平方和选为控制系统的目标函数,表示为:
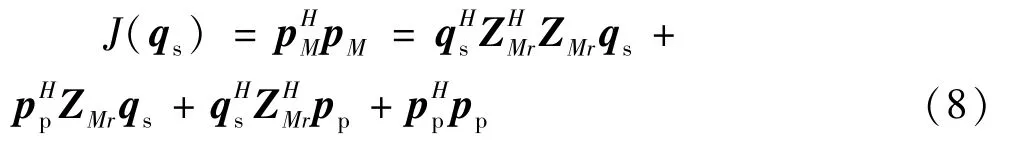
式中J(qs)是次级声源强度qs的二次型函数。求解得到使目标函数最小的最优次级源强度为:
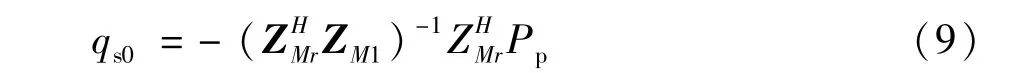
在此次级源强度下,M观测点处的声压为:

为了评价加入次级声源阵列后待消声面的降噪效果,在待消声面上选一组监测点,定义有源噪声控制系统的降噪量(Attenuation Level,AL)[12],其数值LAL越大说明降噪效果越好,降噪量的表达式为:
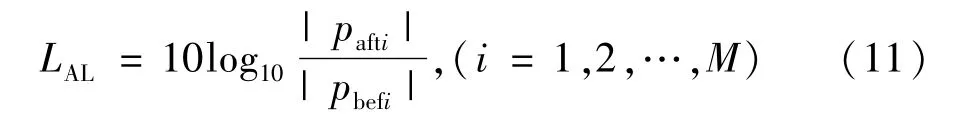
式中pbefi、pafti分别为加入次级声源前后监测点的声压。根据式(11)求得加入次级声源后监测点的降噪量,以近似刻画待消声面的降噪量分布,从而评价布放方案的优劣。
由推导可知,声压表达式(4)、式(6)是与次级声源到观测点的距离直接相关的函数。因此本文提出采用遗传算法优化目标函数(8)求得对应于不同数目次级声源的最优布放位置(即次级声源阵列距变压器中心的距离和阵列中相邻声源之间的纵向间距和横向间距);结合次级声源的位置参数,由式(9)求出对应于此最优布放的最优次级源强度。通过优化得到的次级声源的位置和声源强度,可以最大限度地降低待消声平面的噪声水平。
2 次级声源布放优化
利用上一节建立的变压器声场辐射模型,结合降噪系统现场环境,优化出次级声源的布放参数,获得的布放参数可作为下一节模拟实验的依据。
2.1 位置优化结果及分析
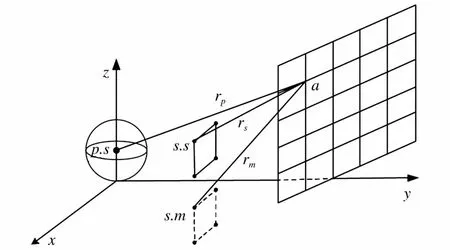
图2 半自由空间声场中有源噪声控制模型示意图Fig.2 Schematic diagram of active noise control model in half free space
结合变压器实际声场环境,可得图2所示变压器声场模型。以地面反射面为xoy平面建立三维空间直角坐标系,初级声源、次级声源阵列均在地面上,本文将变压器简化为脉动球形声源p.s,球源半径r0=2 m,球形模型的球心设置为(0,0,2),球面振动速度ua=6.3×10-4m;次级声源阵列s.s与 xoz平面平行,且次级声源阵列平面的几何中心与球心均在同一条直线;次级声源的“镜像”s.m关于xoy平面对称排列;选取与次级声源阵列平行的10×10 m的平面作为待消声面,其几何中心与球源中心的距离为10 m,将待消声面进行网格划分获得121个观测点;任一次级声源及其“镜像“到观测点a的距离分别为rs、rm;空气密度与声速分别为ρ0=1.29 kg/m3,c0=344m/s。
以待消声面观测点声压平方和为目标函数,设置遗传算法的参数:取种群大小为100,交叉算子采用中间交叉算子,交叉概率Pc=1.0;变异函数采用均匀选择函数(Uniform),变异概率Pm=0.01;选择算子采用均匀选择函数(Uniform),最大迭代次数为100次。对于不同次级声源阵列组合,每组进行10次优化,取平均值作为最终优化结果。选取三个参数作为优化变量:(1)次级声源阵列面到初级声源球心的距离rps,其必须大于球源的半径,即rps>2;(2)相邻次级声源间的横向距离rss1;(3)相邻次级声源间的纵向距离rss2。得到的优化结果如图3所示。
图3中,横坐标表示次级声源个数,纵坐标表示次级声源间距。分析图3可以得到:(1)无论次级声源选择几个,次级声源阵列都应尽量挨近初级声源,这样能使观测点的声压值足够小;(2)次级声源彼此之间的横向间距、纵向间距基本呈现随着数量的增加而逐渐减小的趋势,这样将使得次级声源阵列的几何尺寸不至于太大。

图3 优化结果示意图Fig.3 Schematic diagram of optimization results
2.2 待消声面降噪量分析
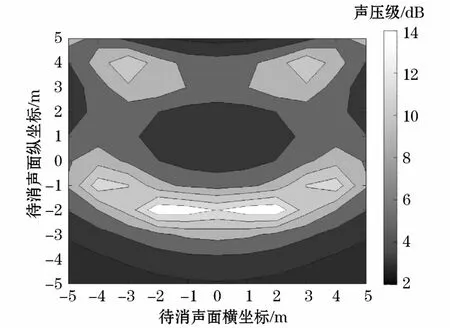
图4 次级声源数量为4时的降噪量分布图Fig.4 Distribution diagram of noise reduction effect with 4 secondary sound sources
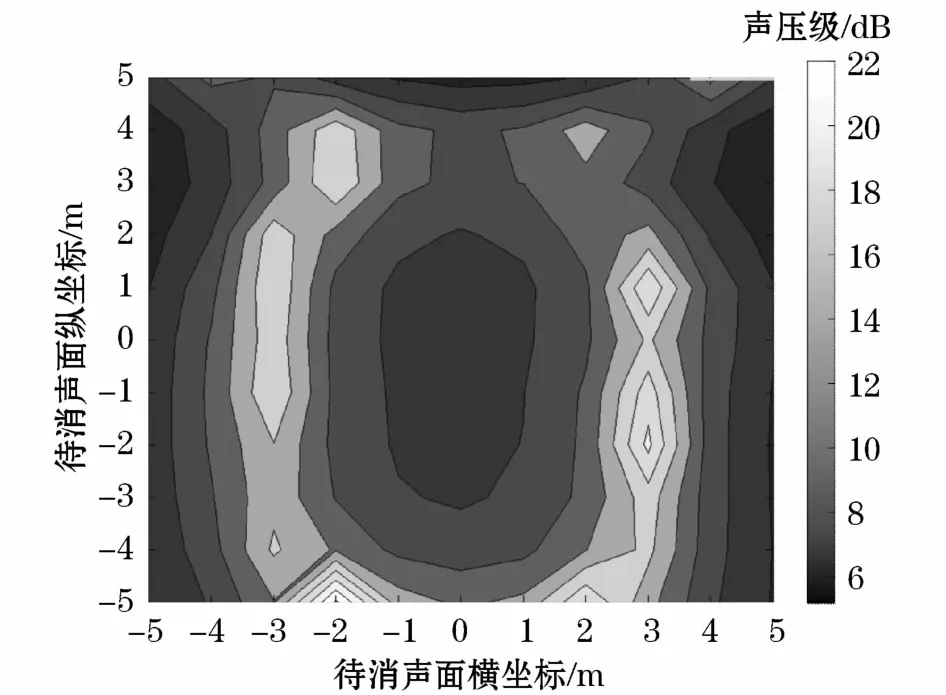
图5 次级声源数量为6时的降噪量分布图Fig.5 Distribution diagram of noise reduction effect with 6 secondary sound sources
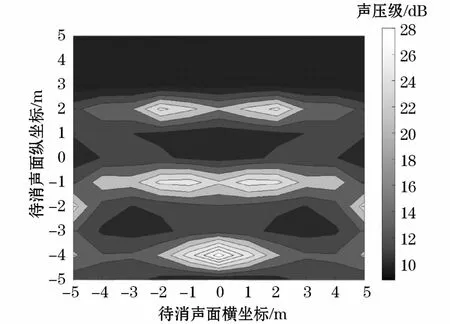
图6 次级声源数量为9时的降噪量分布图Fig.6 Distribution diagram of noise reduction effect with 9 secondary sound sources
将图3的优化结果代入到式(5)~式(11)计算出最优次级声源强度和待消声平面降噪量,得到监测面降噪量的分布图,如图4~图8所示。
结合表1及图4~图8的仿真结果分析总结出如下规律:(1)次级声源数量不同,待消声面获得的降噪量也不同:次级声源数量4和6个时,待消声面大部分观测点降噪量不超过9 dB(A),但是当次级声源数量为9、12和16时,待消声面的降噪量均超过9 dB(A);(2)次级声源数量确定的条件下,待消声面降噪量的分布也大不相同,可以观察到仿真图上半区域的降噪量一般都不大,中心区域和下半区域却有较大的降噪量,可以推测出降噪区域的分布与次级声源的位置是有关联的;(3)当次级声源数量为9时,待消声区域整体已经取得了相当可观的降噪量,因此工程实际中采取此种布放就足够了,既节约了成本,又降低了多通道系统的复杂性和不稳定性。
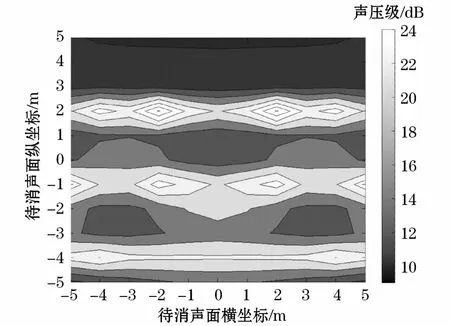
图7 次级声源数量为12时的降噪量分布图Fig.7 Distribution diagram of noise reduction effect with 12 secondary sound sources
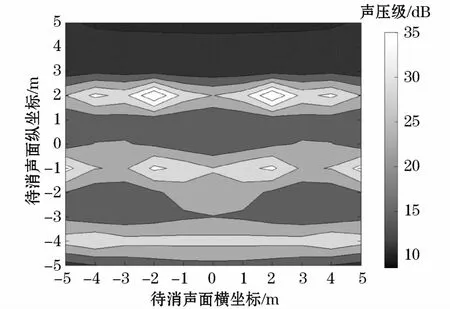
图8 次级声源数量为16时的降噪量分布图Fig.8 Distribution diagram of noise reduction effect with 16 secondary sound sources
根据降噪量的分布图,统计出不同次级声源数量时降噪量的分布情况,如表1所示。
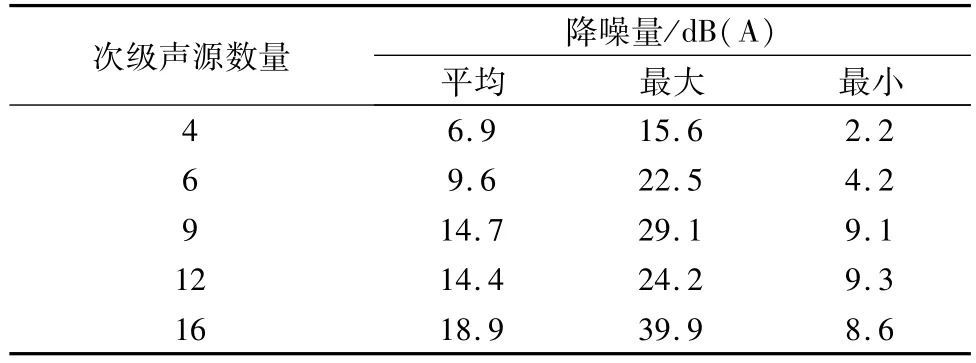
表1 不同次级声源数量的降噪量分布情况Tab.1 Distribution of noise reduction effect with different secondary sound sources
3 次级声源布放实验
3.1 实验条件
为了验证前文优化得到的布放参数的有效性,本节进行了优化布放模拟实验。实验框图如图9所示,信号发生器发出100 Hz单频信号经功率放大器放大以驱动扬声器,参考文献[19]提出的电力变压器低频噪声模拟与等效的方法,通过调节扬声器的相位、幅值以模拟变电站实际噪声水平,该信号同时作为参考信号输入工业控制机作为参考信号;工业控制机计算出次级信号,次级信号经由功放放大输入到扬声器阵列,扬声器阵列作为次级声源;实验场地噪声水平由噪声计测量。
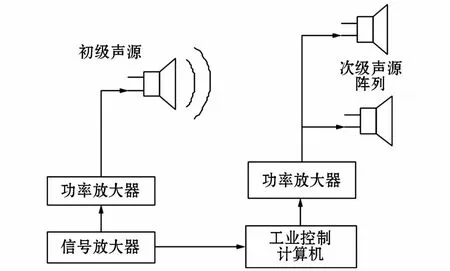
图9 实验系统框图Fig.9 Experimental system block diagram
选取开阔场地作为实验场地,场地周围没有障碍物的干扰,基本符合半自由空间声场环境。模拟实验选用两个扬声器模拟初级声源;次级声源阵列平行于初级声源;选取平行于次级声源阵列且距离初级声源10 m远处的平面区域为待消声区域。为了有效评价待消声面的降噪效果,将待消声面上部5个监测点定为A组、中部5个监测点定为B组、下部5个监测点定为C组,三组共15个监测点,监测点水平间距、垂直间距均为1 m。实验场景如图10所示。
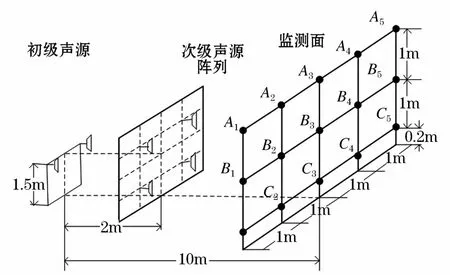
图10 实验场景图Fig.10 Sketch of experimental site
前文提到,9个次级声源得到的降噪量足以满足工程需要,因此实验选取4、6、9个次级声源进行实验。实验条件基本符合前文建立的仿真模型,因此次级声源阵列位置和声源强度根据仿真得到的优化布放参数调节。同时,为了比较优化布放参数的有效性,设置相应的经验布放实验进行对照,具体设置为:调整次级声源阵列与初级声源距离l=2 m;4个次级声源时,相邻次级声源之间的横向距离为0.7 m,纵向距离为1.2 m;6个次级声源时,横向距离为0.6 m,纵向距离为0.4 m;9个次级声源时,横向距离为0.6 m,纵向距离为 0.4 m。
3.2 实验结果及分析
首先开启信号发生器发出初级噪声,利用噪声计测量各监测点的A计权声压级、100 Hz单频噪声声压级。记录完各测点初始噪声数据后,开启次级声源阵列,记录相应的数据。调整次级声源的数量和布放位置,做多组实验。实验结果如图11~图13所示。
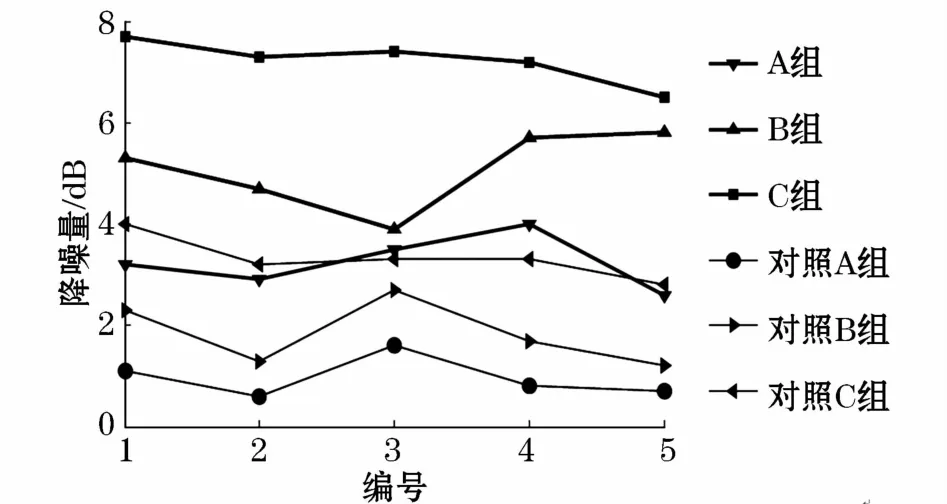
图11 4个次级声源时监测点降噪量Fig.11 Noise reduction of monitoring points with four secondary sources
分析测得的数据可知:
(1)降噪量数据:从纵向来看,B组和C组降噪量较大;从横向来看,编号3对应的位置,降噪量较大。可以认为,越靠近待消声面的几何中心、越贴近地面,降噪量往往越大,与仿真结果相似;
(2)经验布放实验中,随着次级声源数目的增加,降噪量也有所增加,但是经验布放的降噪效果没有优化布放降噪效果好,证明了优化参数的有效性、适用性。
需要指出的是,一般将变电站靠近居民区的区域作为待降噪区域,选择变电站站界作为待消声平面,相应的布放可以在此平面获得最优的降噪效果。布放参数固定后,若向居民区方向平行移动监测面,随着监测面到次级声源阵列距离的增大,初级声源和次级声源在监测点处的辐射声压减小,声传播阻抗减小,所以,监测面监测点总的声压平方和是呈减小趋势的,即监测面总的噪声水平是减小的,可以达到特定区域噪声水平控制的目的。
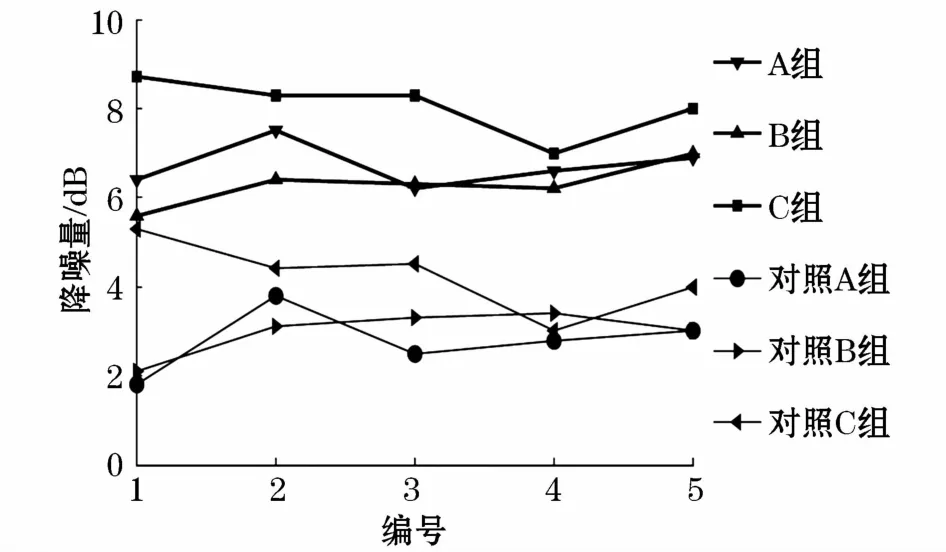
图12 6个次级声源时监测点降噪量Fig.12 Noise reduction of monitoring points with six secondary sources
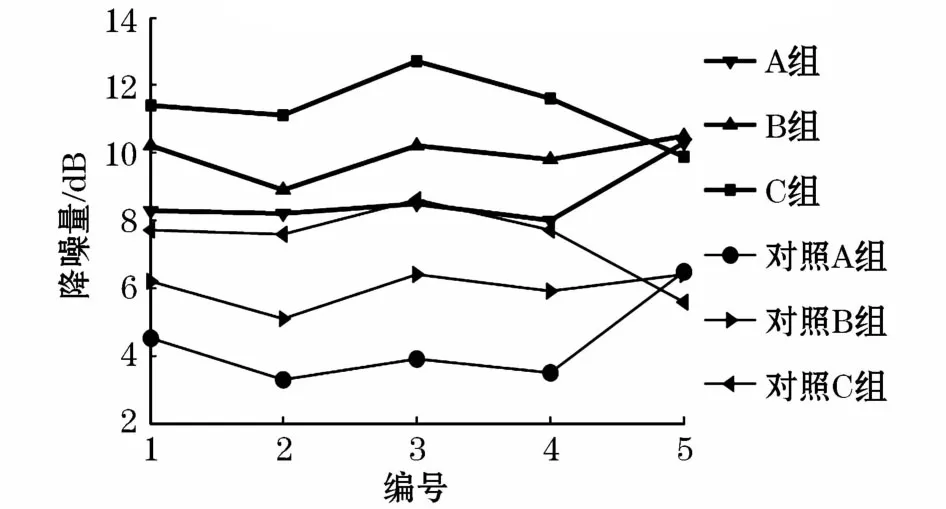
图13 9个次级声源时监测点降噪量Fig.13 Noise reduction of monitoring points with nine secondary sources
4 结束语
在有源降噪系统中,次级声源的优化布放不仅影响降噪系统的稳定性,而且影响噪声控制的效果。本文提出了结合解析法和遗传算法的次级声源优化策略。针对变压器有源降噪实际应用环境,采用优化策略得到不同次级声源数目对应的最优布放方案,并总结了次级声源布放位置和待消声面降噪量分布的规律。为了验证优化布放方案的有效性,进行了100 Hz单频实验,实验模拟了变压器噪声环境,选取10 m远处的平面为待消声面,并设置经验布放方案作为对比实验,通过整理和分析实验数据得知,待消声面的降噪量分布与从仿真结果中总结的规律基本相符,实验取得的可观降噪量验证了布放方案的有效性。
