志愿计算系统时延分析*

(上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室，上海 200240)

志愿计算系统时延分析*

张 健**，李 东，叶 通

(上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室，上海 200240)

志愿计算(Volunteer Computing)系统是一种分布式计算系统，它利用全球空闲计算资源实现海量科学计算。随着志愿计算的广泛应用，系统时延性能分析变得日益重要。现有文献主要通过仿真和实验观察其时延特性，并不能深入分析系统参数的影响。为此，提出了一种新的数学模型对志愿计算系统时延特性进行分析。志愿计算系统可以建模为一个变速率服务的单服务台排队系统。理论分析表明，系统的平均队长与服务速率方差之间存在单调递增的关系。因此，系统在服务速率方差趋于0和无穷大两个极端情况下的平均队长分别为系统平均队长的下界和上界，而在这两种极端情况下，可以通过对系统模型的简化求得系统的平均队长。仿真结果验证了该方法所求平均队长上下界的正确性和准确性。

志愿计算；排队网络；时延分析；服务速率方差；马尔科夫链

1 引 言

近些年，志愿计算(Volunteer Computing，VC)成为学术界进行科学计算的一种新方法。全世界的计算和存储能力不再集中于大型数据中心或者超级计算机,相反，它们现在分布于全世界所有的个人电脑之中[1]。志愿计算利用社会大众个人电脑的空闲计算能力进行科学计算，这种计算方法不仅仅用很低的成本获得了巨大的计算能力，还为社会大众了解科技发展提供了一个途径，也让科学界更加了解社会的实际需求。

志愿计算在20世纪90年代首次出现[1-2]。1999年，加州大学伯克利分校的空间科学实验室创立了SETI@home项目。这个项目将收集到的电磁信号数据分成许多小的工作单元，然后送到世界各地参与该项目的志愿者的电脑上进行分析。志愿者的主机在自己空闲的时间内为这个项目做科学计算的工作。计算任务完成之后，这些主机自动把结果提交回服务器[3]。SETI@home项目成功之后，加州大学伯克利分校的空间科学实验室开发了一个开放平台——BOINC(Berkeley Open Infrastructure for Network Computing)，这个平台可以让其他的科学计算项目更容易使用志愿计算的服务。到2016年11月，约有15 000 000台主机加入了BOINC，其中有1 000 000台主机长期保持在线，平台运行项目超过50个[4]。

随着志愿计算系统的快速发展，其时延的性能分析也变得越来越重要[5]。一些应用如分子动力学仿真[6]和启发式优化算法对系统的时延性能非常敏感，另外一些对实时性要求较高的系统，例如在线导航、在线视频编解码等应用同样要求对系统的时延性能有很好的估计[7]。针对这些业务，已有一些文献[8-10]在传统志愿计算系统的基础上提出了一些新的方法来解决时延较大的问题。目前也有一些分析志愿计算系统时延特性的文献，但这些文献主要是用仿真[11-12]和实验[13-14]进行分析，并没有一个很好的数学模型可以描述志愿计算系统的服务特性。要深入理解志愿计算系统，需要一个完整的数学模型。

在志愿计算系统中，每个任务都是同时被很多志愿者服务，总的服务速率取决于系统中工作中的志愿者的个数。而系统中的志愿者总是随机地到达或离开系统[2，15]，因此，系统的服务能力是随时间变化的。即使在一个任务的服务过程中，系统的服务能力也可能经历很多次变化。本文将志愿计算系统建模为一个变速率服务的单一队列，这个队列的服务器有许多不同的服务状态，每个状态有不同的服务速率，而服务器在不同时间可能处在不同的状态。

这类变速服务的队列在数学上也是很难处理的，难点在于不同任务的服务时间并不是独立同分布的，因此传统的M/G/1队列的求解方法在这里并不适用。为了解决这个问题，文献[16]提出了开始服务概率的概念，但其中提到的开始服务概率只能在某些特殊情况下求得。文献[17]求解了一般情况下两状态服务的开始服务概率，并给出了两状态服务的平均时延公式，但需要求解一组线性微分方程，而我们的模型中有无穷多的状态，线性微分方程组无法求解。

本文基于系统平均队长与服务速率波动之间的联系，给出了系统平均队长的上下界。我们发现在系统的平均服务速率固定的情况下，任务平均服务时间的均值和方差均与服务速率方差正相关。由M/G/1队列的平均队长公式(P-K公式)所给出的，系统的平均队长与任务服务时间的一阶矩和二阶矩正相关。由此，我们建立起系统平均队长与服务速率波动的单调性关系。根据这个关系，我们考虑系统服务速率波动的两个极端状态并得到平均队长的上界和下界：当服务速率的方差趋于0的时候，系统的平均队长趋于下界；反之，当服务速率的方差趋于无穷的时候，系统的平均队长趋于上界。

2 志愿计算系统的马尔可夫模型

2.1 系统描述

志愿计算项目一般都符合如下流程：当一个任务到达之后，它首先在队列中等待。当它处于队头时，就会被分割成许多小的工作单元等待志愿者服务。志愿者总是随机到达，并且在到达之后马上请求需要服务的工作单元。工作单元的分配服从某种特定的分配策略[2]，而在本文中，我们仅考虑先到先服务的策略，即只要有志愿者请求工作单元，就立即将一个工作单元发送给这个志愿者。由于志愿者主机仅在其空闲时才服务工作单元，而且志愿者主机也可能在服务工作单元的过程中就被关机，志愿者接收到工作单元之后也并不能连续不断的服务。但是，数据处理程序会周期性地把运行结果写入文件，并且在重新开始服务的时候读取文件。因此，尽管服务的过程不是连续不断的，数据处理也能完成[3]。当工作单元计算完成之后，志愿者自动将结果提交回服务器，并请求下一个服务单元。

一般来说，志愿计算的项目都是计算密集型的，数据处理时间要远远大于数据传输的时间，因此，在建模分析的过程中，我们忽略了数据和结果传输的时间。例如：在SETI@home这个项目中，工作单元的大小通常为350 KB，而反馈结果的大小只有1 KB左右，数据传输通常几秒之内就可以完成，而这样一个工作单元需要一个志愿者主机运行一天左右的时间[3]。

综上所述，在系统建模中，我们做出如下假设：

(1)任务的到达过程是一个参数为λc的泊松过程；

(2)志愿者的到达过程是一个参数为λs的泊松过程；

(3)志愿者的服务能力都是一致的，均为μc；

(4)志愿者持续工作的时间是一个服从参数为μs的负指数分布的随机变量，志愿者中断服务即被认为离开系统，当其重新开始服务便被认为是一个新的到达；

(5)志愿者的数目很大，可以认为趋近无穷；

(6)志愿者到达之后总是有工作单元可以分配。

图1 志愿者数量的连续时间马尔可夫链Fig.1 The continuous-time Markov chain of the server process

在排队论中，服务器数量可变的系统可以看作是一个有可变服务速率的单一队列。我们将所有的志愿者视为一个大的服务器，而它的服务速率是所有志愿者的服务速率之和。由于志愿者的到达和离去都是随机的，整个系统的服务速率是随时间变化的。系统的服务速率可以这样理解：如果在服务一个任务的过程中，志愿者的数量保持不变，那么任务的服务时间服从负指数分布。但在这个系统中，在服务一个任务的过程中，志愿者的数量是在不断改变的，因此任务服务时间的分布是未知的。而且由于任务服务时间之间存在相关性，排队论中的肯德尔标注(Kendall’s notation)方法已不再适用。

在本文中，我们定义如下符号：

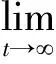
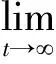
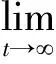
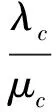
2.2 连续时间马尔可夫链

根据之前的系统描述，图2所示为志愿计算模型的连续时间马尔可夫链，其状态空间为{(i,j),i=0,1,2,…;j=0,1,2,…}，其中i表示系统中任务的个数，j表示系统中志愿者的数量。

图2 志愿计算系统连续时间马尔可夫链Fig.2 The continuous-time Markov chain of the VC queueing model

用pi,j表示系统稳定时，系统处于状态(i,j)的联合稳态概率

pi,j=Pr{nc=i,ns=j}。

(1)

式中：i=0,1,…表示系统中任务的数量，j=0,1,…表示系统中志愿者的数量。由图2所示的状态转移图，可以直接写出系统的平衡方程如下：

(λc+λs)p0,0=μsp0,1,i=0,j=0；

(2a)

(λc+λs)pi,0=λcpi-1,0+μspi,1,i≥1,j=0；

(2b)

(λc+λs+jμs)p0,j=λsp0,j-1+(j+1)μsp0,j+1+jμcp1,j,
i=0,j≥1；

(2c)

(λc+λs+jμs+jμc)pi,j=λspi,j-1+λcpi-1,j+(j+1)μspi,j+1+jμcpi+1,j,i≥1,j≥1。

(2d)

定义pi,j的生成函数为

(3)

根据公式(2)的平衡方程，可以直接推导出关于生成函数F(z1,z2)的一个差分方程：

(λc-z1λc+λs-z2λs)F(z1,z2)=

(4)

目前，我们无法通过这个差分方程得到F(z1,z2)的表达式，从而确定系统的平均队长。我们仅能从这个差分方程中得到一些方便后续处理的公式。

首先，等式(4)左右两边同时对z1求导并代入z1=z2=1，可以得到

(5)

类似地，等式左右两边同时对z1求二阶导并代入z1=z2=1，可以得到

(6)

由公式(5)和(6)可得

ρcE[nc]=E[nsnc]-ρc。

(7)

这里，由于系统中任务的数量与志愿者的数量是相关的，即无法求得E[nsnc]，因此系统的平均队长E[nc]仍然无法求解。

得到式(7)，说明传统的排队论求解方法在求解这个问题的过程中需要知道任务的数量与志愿者数量的相关性，而这正是问题的困难之处。因此，我们只能尝试从其他的角度求解该排队模型。

3 服务速率波动和时延的上下界

对于志愿计算系统的排队模型，求解系统平均队长的难点在于任务服务时间的分布是未知的，而且任务的服务时间之间存在相关性。我们已知的信息只有在系统稳态下志愿者数目的分布是泊松分布，因此在本节中，我们首先探究服务速率的波动与系统平均队长之间的关系，然后据此得到系统平均队长的上界和下界。

3.1 服务速率波动的影响

直观上来看，服务速率的波动越大，服务时间的均值和方差都会越大。事实上，如果固定平均服务速率不变，服务时间的均值和方差随服务速率的方差增大而增大，本节将说明这个性质成立。

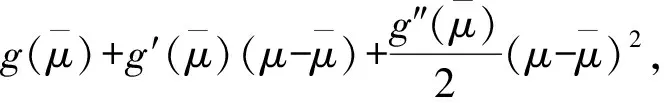
(8)

那么g(μ)的均值和方差可以近似表示为

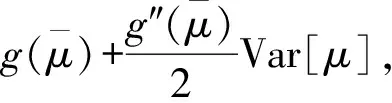
(9a)

(9b)

因此，服务时间的均值和方差S=g(μ)=1/μ近似表示为

(10a)

(10b)

对于一个到达速率为常量的排队系统，系统的平均队长与服务时间的均值和方差成正相关。M/G/1排队模型的平均队长公式——P-K公式阐述的就是这一性质[18]：

(11)

但P-K公式的成立，要求每个任务的服务时间是独立同分布的随机变量，而这个条件在志愿计算的模型中并不成立。因此，如果简单地将上面推导出的服务时间均值和方差的近似直接代入P-K公式，结果与真实情况会相差很大。尽管通过上述分析没有得到志愿计算模型的平均队长，但得到的单调性关系可以帮助我们得到平均队长的上界和下界。

3.2 时延上下界

我们知道系统中志愿者的个数ns是一个服从均值为ρs的泊松分布的随机变量，因此可以得到如下参数的表达式：

(a)μc=0.1

(b)μc=1图3 系统服务速率随时间波动 (μc/μs=10,λs=10)Fig.3 The fluctuation of service rate μ

直观来讲，μc和μs较大意味着每一个志愿者的服务速率都比较大而系统中存在的志愿者个数比较少。在这种情况下，每一个志愿者的到达或者离去都将使系统的服务速率发生较大的变化；反之则每一个志愿者的服务速率都比较小，那么志愿者的到达和离去对服务速率的影响就比较小，这样系统的服务速率就更加稳定。

当保持μc与μs的比值和λs不变时，系统的平均队长将随着服务速率波动的增大而增大。因此，我们分析两种极端情况：当μc→0时，系统将达到平均队长的下界；当μc→时，系统将达到平均队长的上界。

当固定保持μc与μs的比值和λs不变时，系统的平均服务速率保持不变，在这种情况下，当μc→0时，系统应表现出如下服务行为：

由于ρs→，系统中志愿者的个数较多；

由于μs→0，每个志愿者连续服务的时间较长；

由于μc→0，每一个志愿者的服务能力都比较小。

图4 系统处于平衡态时系统的服务速率近似于常量Fig.4 Service rate becomes a constant when system reaches equilibrium

(12)

上式等价于

(13)

因此，有

(14)

系统稳定时，系统的平均队长总是有限的，因此当ε→0时，有

(15)

因此，

(16a)

(16b)

由等式(7)和(16b)可得，此时的系统的平均队长，也即系统平均队长的下界为

(17)

当固定μc与μs的比值和λs不变时，系统的平均服务速率保持不变，在这种情况下，当μc→时，系统应表现出如下服务行为：

由于ρs→0 ，系统中志愿者的个数较少；

由于μs→，每个志愿者连续服务的时间较短；

由于μc→，每一个志愿者的服务能力都比较大。

图5描述了这种情况下系统中的志愿者行为。由于每个志愿者连续服务的时间很短，系统中存在两个或两个以上志愿者同时服务的概率很小，系统可以近似等价于仅有一个志愿者，而它有时在服务，有时不在服务。

图5 服务速率在极端情况下只有两个状态Fig.5 The two-state extreme scenario of VC systems

由于系统中仅有的志愿者都有很大的服务速率，系统仍能保证稳定的运行。从数学及角度来讲，因为系统中志愿者的个数服从泊松分布，在极端情况ρs→0的情况下，系统中志愿者个数在2个或2个以上的概率为

Pr{ns≥2}=o(ρs2)→0。

(18)

因此，系统中志愿者个数大于1的概率可以忽略，因此服务模型可以简化为一个两状态的服务。图1所示的马尔可夫链也就简化为图6所示形式。

图6 两状态服务系统的状态跳转Fig.6 The transition diagram of the two service states

对于两状态变速服务的系统，很多文献都有详细的分析，例如文献[17，19]。文献[17]给出了系统处在状态0和状态1时系统中任务个数的生成函数如下：

(19a)

(19b)

此时系统的平均队长，也即志愿计算模型的平均队长的上界L2可以通过如下方式得到：

(20)

对式(19)求导并代入z=1，再取μc,μs→的极限即可得到平均队长的上界

(21)

至此，已经得到平均队长的上界和下界。我们同样用离散事件仿真验证了这个上界和下界的正确性和准确性。固定μc/μs=10和λs=10，任务到达速率λc在10～90中取值。图7中下界和上界分别是公式(17)和(21)的计算结果，其余曲线为仿真结果。仿真结果表明，系统的平均队长随μc值的增大而增大，当μc→时，系统平均队长趋近于上界L2；而当μc→0时，系统平均队长趋于下界L1。

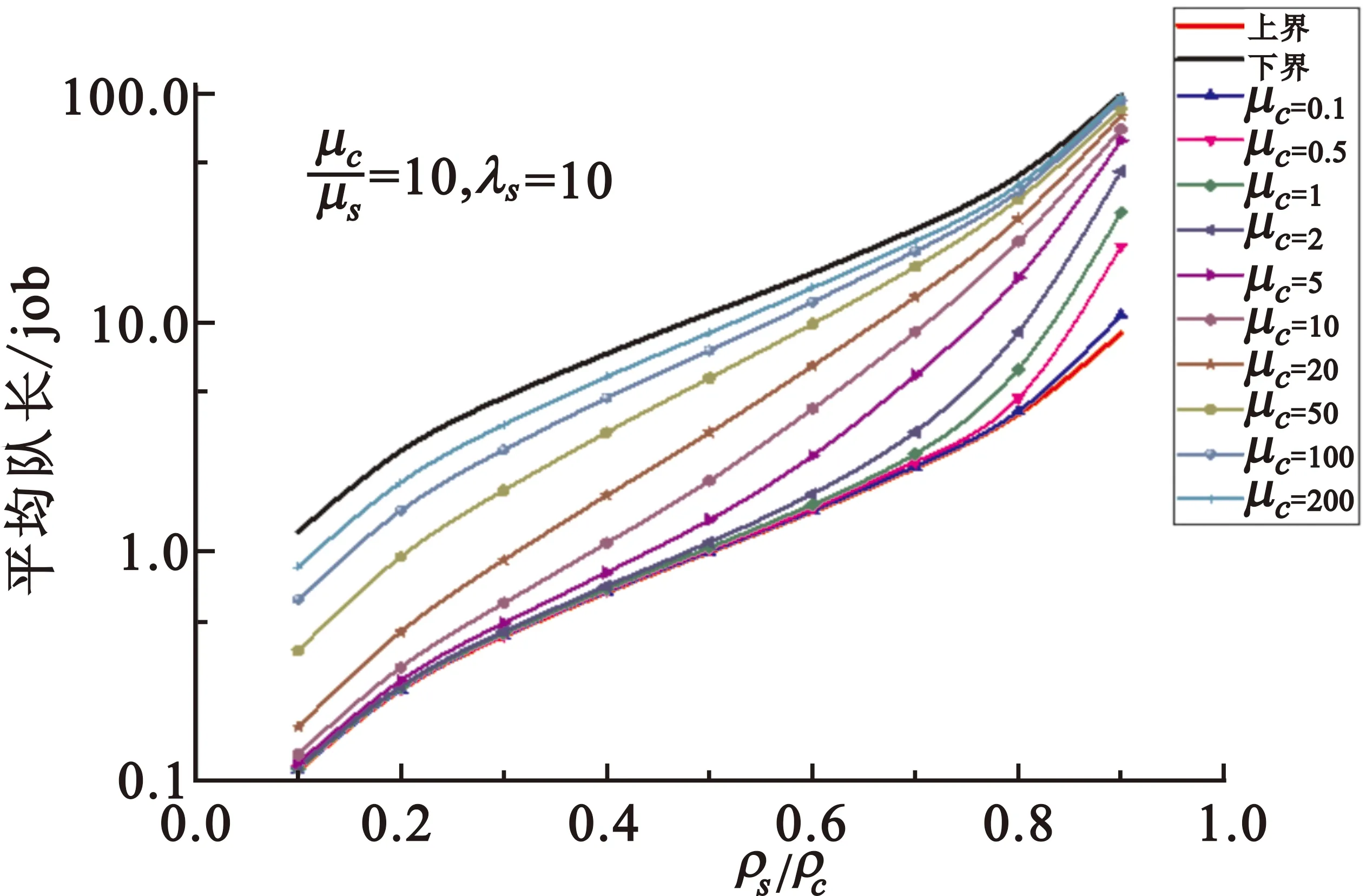
图7 系统平均队长L1≤L≤L2Fig.7 Mean queue length L is bounded by L1 and L2

从系统平均队长的上界和下界中也可以得出系统稳定的条件为

ρc<ρs,

(22a)

或者等价的

(22b)

这个条件保证了系统平均队长的上界和下界均是正值且有限。同时，这个结论也符合我们对系统的直观认识，只要系统的平均到达速率小于系统的平均服务速率，无论系统的服务速率如何波动，系统总能保证是稳定的。

4 结束语

本文对志愿计算系统建立了二维马尔可夫模型，在这个模型中，系统的任务和服务器均随机到达和离开。然而，这个系统在数学上是无法得出平均队长的表达式的。受M/G/1队列的平均队长表达式P-K公式的启发，我们建立起系统的平均队长与系统服务速率波动之间的关系，并在极端情况下得到了系统平均队长的上界和下界。

目前，随着计算机系统越来越复杂，用可变速率服务的系统对实际网络应用的建模变得越来越困难。除了一些很简单的模型之外，大部分可变速率服务的系统在数学上都是无法求解的。因此，我们的方法可能会给以后求解这类问题提供一个新的方法，虽然无法得到平均队长的表达式，但可以很直观地给出一个平均队长的估计。也希望我们的方法将能在如云计算和节能以太网等其他领域的建模中有所应用。

后续工作包括具体求解志愿计算系统模型的平均队长或尝试得到平均队长的一个近似以及尝试用文中的方法对其他类似的变速服务系统进行分析。

[1] ANDERSON D P. Boinc:a system for public-resource computing and storage[C]//Proceedings of Fifth IEEE/ACM International Workshop on Grid Computing.Pittsburgh,PA,USA:IEEE,2004:4-10.

[2] DURRANI M N,SHAMSI J A. Volunteer computing:requirements,challenges,and solutions[J].Journal of Network and Computer Applications,2014,39(1):369-380.

[3] ANDERSON D P,COBB J,KORPELA E,et al.SETI@ home:an experiment in public-resource computing[J].Communications of the ACM,2002,45(11):56-61.

[4] WILLY D Z. BOINCstats[EB/OL]. (2014-07-15)[2017-04-15].http://boincstats.com.

[5] ESTRADA T,TAUFER M,REED K. Modeling job lifespan delays in volunteer computing projects[C]//Proceedings of the 2009 9th IEEE/ACM International Symposium on Cluster Computing and the Grid.Shanghai:IEEE,2009:331-338.

[6] VIJAY P.Folding@home[EB/OL]. (2000-09-19)[2017-04-15].http://folding.stanford.edu/.

[7] YI S,JEANNOT E,KONDO D,et al.Towards real-time,volunteer distributed computing[C]//Proceedings of the 2011 11th IEEE/ACM International Symposium on Cluster,Cloud and Grid Computing.Newport Beach,CA,USA:IEEE,2011:154-163.

[8] BRUNO R,FERREIRA P. FreeCycles:efficient data distribution for volunteer computing[C]//Proceedings of the Fourth International Workshop on Cloud Data and Platforms. New York:ACM,2014:1-6.

[9] TARIGAN J T,JAYA I,HARDI S M. Distributed Rendering on Volunteered Mobile Resources[C]//Proceedings of the 5th International Conference on Communications and Broadband Networking.Bali Island,Indonesia:ACM,2017:25-29.

[10] HEIEN E M,FUJIMOTO N,HAGIHARA K. Computing low latency batches with unreliable workers in volunteer computing environments[C]//Proceedings of 2008 IEEE International Symposium on Parallel and Distributed Processing.Miami,FL,USA:IEEE,2008:1-8.

[11] ESTRADA T,TAUFER M,ANDERSON D P. Performance prediction and analysis of BOINC projects:an empirical study with EmBOINC[J].Journal of Grid Computing,2009,7(4):537-554.

[12] MONSALVE S A,CARBALLEIRA F G,MATEOS A C. Analyzing the performance of volunteer computing for data intensive applications[C]//Proceedings of 2016 International Conference on High Performance Computing & Simulation (HPCS).Innsbruck,Austria:IEEE,2016:597-604.

[13] GULLAPALLI S. Atlas:an intelligent,performant framework for web-based grid computing[C]//Proceedings of the 2016 24th ACM SIGSOFT International Symposium on Foundations of Software Engineering.Seattle,WA,USA:ACM,2016:1154-1156.

[14] DURRANI M N,IQBAL T,SHAMSI J A,et al.Towards real-time result verification using checkpointing in volunteer computing systems[C]//Proceedings of 2015 IEEE 18th International Symposium on Real-Time Distributed Computing (ISORC).Auckland,New Zealand:IEEE,2015:218-227.

[15] JAVADI B,KONDO D,VINCENT J M,et al.Discovering statistical models of availability in large distributed systems:an empirical study of seti@home[J].IEEE Transactions on Parallel and Distributed Systems,2011,22(11):1896-1903.

[16] MAHABHASHYAM S R,GAUTAM N. On queues with Markov modulated service rates[J].Queueing Systems,2005,51(1):89-113.

[17] HUANG L,LEE T T. Generalized pollaczek-khinchin formula for markov channels[J].IEEE Transactions on Communications,2013,61(8):3530-3540.

[18] KLEINROCK L.Computer applications[M]//Queueing systems:volume 1. New York:Wiley,1975:167-240.

[19] GUNASEELAN N,LIU L,CHAMBERLAND J F,et al.Performance analysis of wireless hybrid-ARQ systems with delay-sensitive traffic[J].IEEE Transactions on Communications,2010,58(4):1262-1272.

DelayAnalysisofVolunteerComputingSystems

ZHANG Jian,LI Dong,YE Tong

(State Key Laboratory of Advanced Optical Communication Systems and Networks, Shanghai Jiaotong University,Shanghai 200240,China)

Volunteer computing (VC) is a distributed computing system which uses spare computing power from general public to do scientific computing. With the rapid growth of volunteer computing,delay performance evaluation becomes more and more important. In existing literatures,delay performance of VC system is majorly observed by simulations and experiments,through which the influence of system parameters cannot be deeply analyzed. Therefore,a new model is proposed to analyze the delay performance of VC system. The VC system can be modeled as a single server queue with variable service rate. Analytical results show that the mean queue length increases with the fluctuation of service rate. Therefore,the mean queue length under two extreme cases,variance of service rate approaches to 0 and infinity,should be the lower bound and upper bound respectively. And the mean queue length under the two extreme cases can be obtained by the simplified system model. Simulation result validates that the two queue length bounds are both valid and accurate.

volunteer computing;queueing network;delay analysis;fluctuation of service rate;Markov chain

10.3969/j.issn.1001-893x.2017.12.002

张健，李东，叶通.志愿计算系统时延分析[J].电讯技术，2017,57(12):1356-1362.[ZHANG Jian,LI Dong,YE Tong.Delay analysis of volunteer computing systems[J].Telecommunication Engineering,2017,57(12):1356-1362.]

2017-05-04；

2017-07-11

date:2017-05-04；Revised date：2017-07-11

2011aad@sjtu.edu.cnCorrespondingauthor2011aad@sjtu.edu.cn

TN919

A

1001-893X(2017)12-1356-07

张健(1992—)，男，内蒙古包头人，2015年于上海交通大学获学士学位，现为硕士研究生，主要研究方向为分布式计算网络、排队论;

Email：2011aad@sjtu.edu.cn

李东( 1948—) ，男，中国台湾台北人，分别于1976年和1977年获纽约理工大学硕士学位和博士学位，1977～1983年于美国AT&T贝尔实验室工作，1983～1993年在Bellcore (现为Telcordia Technologies)工作，1991～1993 年于纽约理工大学任教授，1993～2010年于香港中文大学任讲席教授，现为上海交通大学致远讲席教授、IEEE Fellow、HKIE Fellow，主要研究方向为宽带交换理论、网络性能分析、无线通信网络；

叶通( 1976—) ，男，福建浦城人，分别于1998 年和2001年获电子科技大学学士学位和硕士学位，2005年于上海交通大学获博士学位，现为上海交通大学副教授，主要研究方向为宽带交换网络结构、网络算法设计和性能分析和光网络系统。