星载AIS信号的频偏估计*

2017-12-20马社祥鑫2王俊峰

电讯技术 2017年12期

关键词：码元谱线时延

马社祥，陈明**，孟鑫2，王俊峰

(1.天津理工大学电气电子工程学院，天津 300384;2.天津理工大学海运学院，天津 300384)

星载AIS信号的频偏估计*

马社祥1，陈明**1，孟鑫2，王俊峰1

(1.天津理工大学电气电子工程学院，天津 300384;2.天津理工大学海运学院，天津 300384)

星载自动识别系统(AIS)中信号存在严重的多普勒频偏，影响信号的正确解调，而传统的基于快速傅里叶变换(FFT)的频偏估计算法其估计范围无法满足需要。为此，提出了一种改进的自相关-FFT频偏估计算法，通过构造辅助函数以确定信号频偏的正负号，在此基础上对基于FFT的频偏估计算法进行改进，从而扩大频偏估计范围，实现对大的多普勒频移的估计。仿真和实验结果均表明，改进算法的频偏估计范围扩大为原来的2倍，具有很高的估计精度，十分接近修正后的克拉美罗界，且算法简单、易于实现。

星载自动识别系统；频偏估计；大多普勒频移；快速傅里叶变换

1 引言

自动识别系统(Automatic Identification System,AIS)是一种工作在甚高频(Very High Frequency,VHF)频段，采用自组织时分多址(Self-organized Time Division Multiple Access,SOTDMA)现代通信技术的广播式自动报告系统。AIS系统用于岸-船、船-岸及船-船间的通信，其工作半径约为40 n mile[1]。为了能够对远海甚至全球范围内船舶进行有效监测，以卫星平台为依托，建立星载AIS系统是一个很好的选择。

星载AIS系统由一颗或多颗低轨道卫星构成[2]，AIS接收机搭载在卫星上以实现对船舶AIS信号的接收、解调和解码AIS报文。而卫星轨道高度一般为600～1 000 km，且卫星的运行速度为7.5 km/s[3]，因此星载AIS信号的最大多普勒频移约为±4 kHz。由于太空环境复杂，信号传输衰减较大，使得接收信号的信噪比较低[4]。因此，为了减少频偏对信号解调及解码造成的影响，星载AIS接收机在进行信号解调前必须进行频偏的估计与校正，以便获得正确的码元序列，从而保证对海上船舶的有效监控。

对于频偏估计，文献[5]基于最小二乘原理，通过计算相邻信号间的相位差得到频偏信息。该算法虽具有较大的频偏估计范围，但其估计性能受噪声影响较大，在低信噪比下估计性能很差，无法满足星载AIS系统的需要。文献[6]利用AIS信号中的训练序列等已知信息消除接收信号的相位信息，在获得频偏主值和扩展部分的基础上，通过数据拟合的方法消除快速傅里叶变换(Fast Fourier Transform,FFT)运算的栅栏效应，得到准确的频偏估计值，但算法的运算量较大，且其估计精度依赖于较长的数据长度。1999年，Morelli等[7]利用已估计出的时延值确定合适的采样点，然后做该采样点处的自相关运算得到频偏估计值，但该算法的频偏估计精度较低，且估计范围仅为码元速率的四分之一。2003年，彭华等人[8]对接收信号做自相关运算以获取频偏主值，然后利用离散傅里叶变换(Discrete Fourier Transform,DFT)对频偏进行修正，虽然该算法的频偏估计精度较高，但估计范围仅为码元速率的四分之一，无法满足星载AIS系统的需求。上述算法中，文献[5-6]是数据辅助下的参数估计算法，虽然估计范围可以满足星载AIS系统的需要，但需要先验信息，而在实际应用中很难获得，因此其估计性能无法保证；文献[7-8]是非数据辅助下的参数估计算法，虽不需先验信息，但其估计范围十分有限，无法满足星载AIS系统的需要。因此，研究出一种满足星载AIS系统频偏范围的非数据辅助的频偏估计算法将会有很好的应用前景。

为了能够估计星载AIS信号的频偏，本文通过构造辅助序列确定接收信号频偏符号，并与FFT算法相结合，进而得到改进算法。改进算法的频偏估计范围从(-1/(4Tb),1/(4Tb))变为(-1/(2Tb),1/(2Tb))，Tb为码元周期，使其能够满足星载AIS系统的需要，且提高了估计精度。在实验室环境下利用已有实验仪器对星载AIS信号进行模拟，实验结果表明，改进算法的估计精度较高，与理论仿真基本一致，具有很高的应用价值。

2 信号模型

星载AIS系统采用GMSK调制方式[9]，基带信号的复包络可表示如下：

s(t)=ejφ(t,α),nTb≤t≤(n+1)Tb。

(1)

式中：φ(t,α)是信号的相位信息，可表示为

(2)

式中：α={αi}为信息序列，取值为{+1,-1}；Tb是码元周期；h是调制指数，在GMSK调制中h=0.5；相位脉冲响应

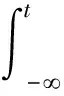
(3)

(4)

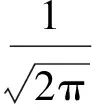
(5)

式(4)中：h(t)为高斯滤波器的矩形脉冲响应，其取值范围为(0,L1Tb)；L1为高斯滤波器持续码元个数;Bb为高斯滤波器的3 dB带宽。

假设s(t)在AWGN信道中传输，星载AIS接收机接收到的信号为

x(t)=ej(2πfet+θ)s(t-τ)+n(t) 。

(6)

式中：fe为频偏，θ为相移，τ为时延，η(t)为高斯白噪声。

对接收信号采样，可得

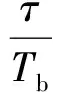
(7)

式中：T为采样周期，且T=Tb/Ns，Ns是过采样因子；将x(nT)简记为x(n)。

3 基于FFT的频偏估计算法

2003年，彭华等人[8]提出了一种利用相位展开和周期图进行频偏估计的方法。该算法是非数据辅助下的频偏估计算法，是对接收信号进行处理，通过构造辅助序列消除调制相位信息的影响，得到含有频偏信息和相移信息的信号。

文献[8]给出了FFT算法的频偏估计的推导公式，即

(8)

式中：

(9)

(10)

(11)

z(n)=(-1)nx2(n) 。

(12)

式中：x(n)是式(7)得到的采样信号(过采样因子为Ns)，m为延迟周期。

因此根据文献[8]知，频偏的估计范围为

(13)

当m较大时，本算法的估计范围约为(-1/(4Tb),1/(4Tb))。由于此算法的估计范围无法满足星载AIS信号的需要，因此对该算法进行改进。

4 改进算法及其实现

仿真时均采用AWGN信道，码元序列长度N=256 bit，过采样因子Ns=8，码元周期Tb=(1/9 600) s，高斯滤波器持续码元长度L1=3，归一化3 dB带宽为BT=0.4。进行了500次蒙特卡罗实验，且本节和第4节中的各图均是采用此条件仿出的。其中，仿真平台选用CPU为AMD Athlon(tm)II X4 640，主频为3.0 GHz，内存为8 GB的电脑；仿真软件采用MATLAB 7.11，仿真条件均参考ITU-R M.1371-4建议书设置的，且码元序列长度选用一个标准时隙的长度。图1是FFT算法在[-4 800 Hz,4 800 Hz]内的频偏估计仿真结果。从图1可以看出，此算法的估计值关于原点近似中心对称，且当频偏大于0而小于2 400 Hz时，其能较准确地估计；当频偏大于2 400 Hz时，其估计值小于0，无法估计出频偏。而负频偏与正频偏的情况刚好相反，在小于-2 400 Hz时，其估计值大于0;而大于-2 400 Hz时，能较准确地估计。如果我们能够根据接收信号构造一个辅助函数，以明确频偏的符号，那么就能将原算法的估计范围扩大1倍。

图1 FFT算法在[-4 800 Hz,4 800 Hz]内的频偏估计分布图Fig.1 Frequency offset estimation of FFT algorithm in [-4 800 Hz,4 800 Hz]

为解决这一困难，由式(7)中的采样信号x(n)构造辅助序列y(n)，即

y(n)=(-1)nx(n),n=0,1,…,L-1,

(14)

则y(n)的DFT为

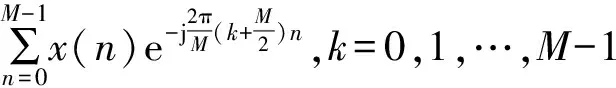
(15)

式中：M为DFT变换的点数，由频域采样定理可知，M≥L。

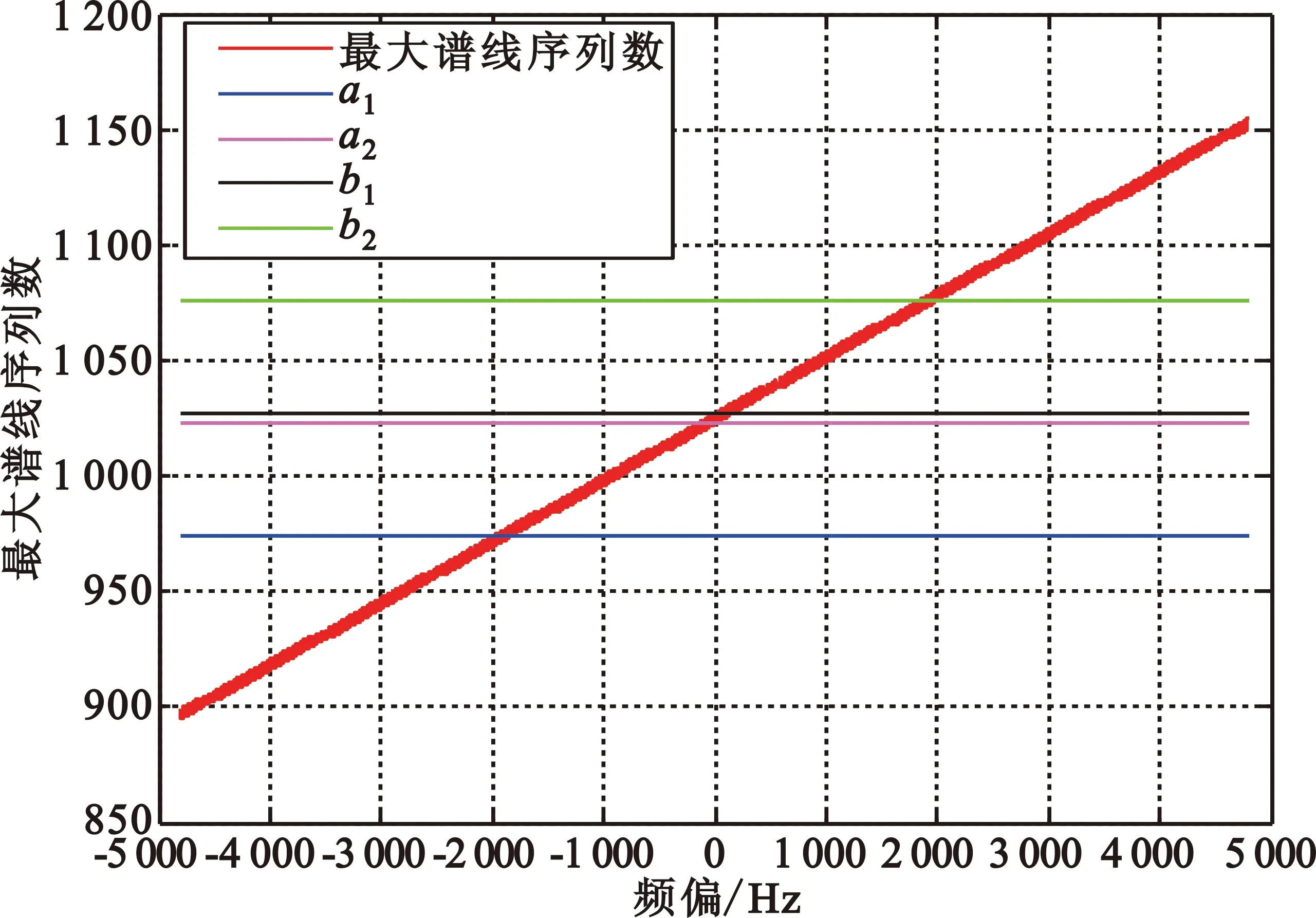
确定Y(k)的最大谱线的位置，记为最大谱线序列数[8]。Y(k)的最大谱线序列数分布图如图2所示。

图2 不同频偏的最大谱线序列数分布图Fig.2 Distribution of the sequence number of the largest spectral line in different frequency offsets

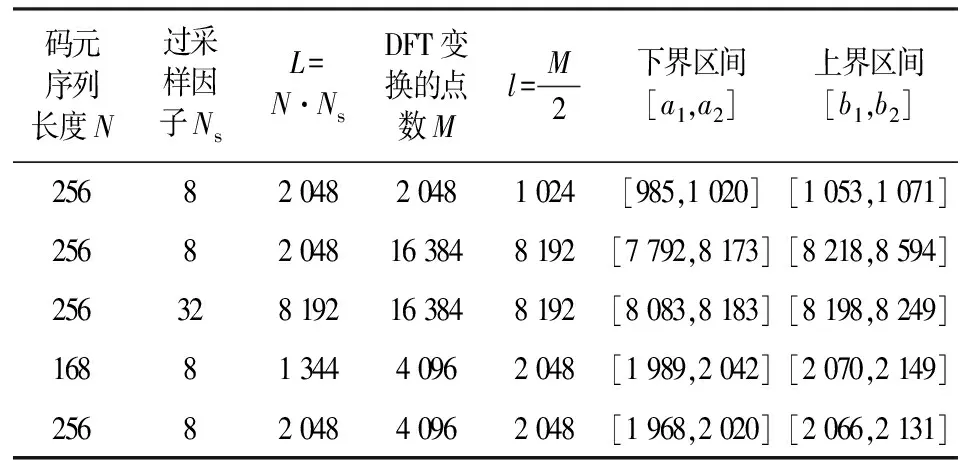
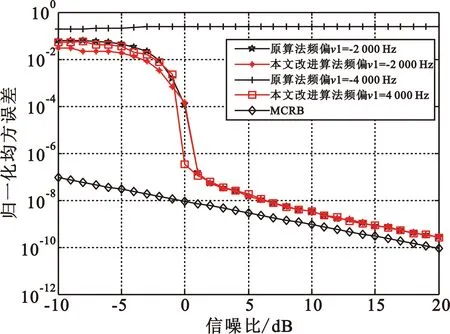
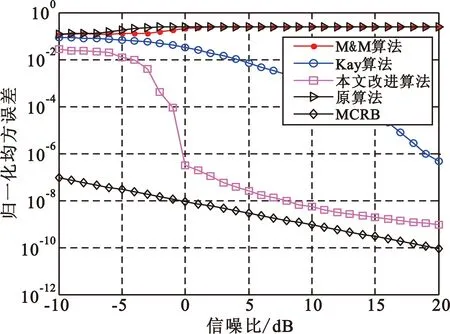
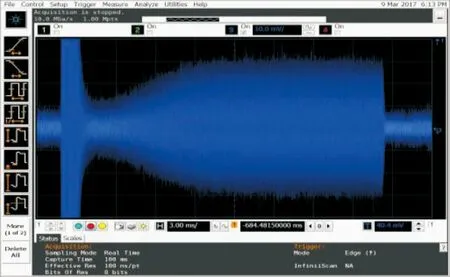
从图2中可以看出，频偏在[-4 800 Hz,4 800 Hz]的最大谱线序列数S1总体呈现单调上升的趋势。最大谱线序列数是频偏为v的信号x(n)经式(14)变换得到的y(n)的频谱谱峰所对应的最大谱线位置，而每一个频偏值对应一个最大谱线序列数，将频偏从-4 800 Hz到4 800 Hz所对应最大谱线序列数放在一张图中显示就构成了最大谱线序列数分布图。图2中横坐标频偏与纵坐标最大谱线序列数是一一对应的。在图2中，在[0 Hz,4 800 Hz]范围内S1的最小值记为a，而在[-4 800 Hz,0 Hz]内S1的最大值记为b。如果a>b，那么S1≥a时，频偏为正，S1≤b时频偏为负。然而事实上a≤b，在[a,b]内频偏的符号无法确定；而当S1>b时，频偏为正，S1

表1 不同信噪比下a和b的取值范围Tab.1 Rang of a and b in different SNR

在表1中，最大下界a2是Y(k)的最大谱线序列数在正频偏的最小值，最小下界a1是频偏小于-2 000 Hz时的最大值；最小上界b1是负频偏的最大值，最大上界b2是频偏大于2 000 Hz时的最小值。a1、a2、b1和b2如图3所示。

图3 确定上下界的最大谱线序列数分布图Fig.3 Determine the sequence number of the largest spectral line distribution of upper and lower bounds

假设式(7)得到的采样后的信号x(n)的长度为L，码元序列长度为N，过采样因子为Ns，因此有L=N·Ns，然后对y(n)做M(M≥L)点DFT得到Y(k)。其中，对于表1，N=256，Ns=8，有M=L=2 048。

表2中各情况均采用表1的方法得到，未给出每种情况的详细数据。结合表2中的结果，通过分析影响a和b的因素(码元序列长度为N，过采样因子为Ns，DFT变换的点数M)可知，a和b最终仅与DFT变换的点数M直接相关；a和b的取值应在表2中各自上下界区间内，故而确定a和b的值分别为l-30和l+30，而l=M/2，且以下各节均采用此进行仿真分析与实验分析。

表2 不同因素下a和b的取值范围Tab.2 Rang of a and b in different situation

综上所述，最终频偏估计值可确定如下:

(16)

5 仿真与性能分析

仿真条件同第4节。为了比较算法性能，定义频偏估计的克拉美罗界[3](MCRB)如式(17)所示：

(17)

从图4中可以看出，本文改进算法在大频偏时依然具有较高的估计性能，并扩大了频偏的估计范围，优于原算法[8]，可对星载AIS信号大的多普勒频偏进行估计，并且该算法不需先验信息，适用于频偏的盲估计。

图4 原算法与本文改进算法的频偏估计性能比较Fig.4 Frequency offset estimation performance comparison between the original algorithm and the improved algorithm

图5是不同时延下本文改进算法的频偏估计归一化均方误差曲线图，可以看出，本文改进算法所能承受的最大时延为(3/8)Tb；当时延在(3/8)Tb以内时，随着时延的增大，本文改进算法的频偏估计性能有所下降，但在信噪比大于5 dB时依然具有较好的估计性能。

图5 时延对频偏估计性能的影响Fig.5 Effect of delay on frequency offset estimation performance

图6是M&M算法[7]、Kay算法[5]、本文改进算法和原算法在频偏为3 000 Hz时的频偏估计性能比较图。从图6可以看出，本文改进算法的频偏估计性能明显优于另外三种算法，且很接近修正后的克拉美罗界。

图6 4种算法的频偏估计性能的比较Fig.6 Frequency offset estimation performance comparison among four algorithms

6 实验验证与结果分析

实验室已有的船台与基站等设备无法产生频偏较大的星载AIS信号，因此利用数字信号发生器产生星载AIS信号，并使用示波器接收并采集信号，将采集到的信号进行下变频等处理，再将处理后的信号用于本文所提出的算法上，以检验本文算法的性能。

对于载波频率fc=161.975 MHz，模拟频偏fd=4 000 Hz的信号，使用示波器得到的信号的中心频率为1.979 MHz，其时域波形如图7所示。将采集到的信号下变频到基带，经FIR低通滤波器滤波后得到的基带信号的频谱如图8所示。使用本文改进的算法估计接收信号频偏并校正，校正后的信号的频谱图如图9所示。图7～9是对使用示波器采集到的信号的分析，从图中可以看出，本算法能较准确地估计接收信号的频偏。实验所使用的信号是按照ITU-R M.1371-4建议书利用MATLAB产生，然后使用数字信号发生器模拟发射源，并用示波器接收信号；实验环境较理想，未考虑时延的影响，所以该改进算法在真实环境中的性能还有待进一步研究。

图7 示波器采集的AIS信号时域波形图Fig.7 Waveform of AIS signal acquired by oscilloscope

图8 包含4 000 Hz频偏的基带信号的频谱图Fig.8 Spectrum of baseband signal containing a frequency offset of 4 000 Hz

图9 校正频偏后的基带AIS信号的频谱图Fig.9 Spectrum of the baseband AIS signal after correcting frequency offset

在相同实验环境下，当所设定的频偏值为2 000 Hz和4 000 Hz时，分别采集5组数据用于本文改进算法、M&M算法[7]和两步求精算法[10]的频偏估计性能比较，其结果如表3所示。从表3可以看出，本文改进算法的频偏估计性能要优于M&M算法和两步求精算法，与理论仿真基本一致，具有较高的估计性能。

表3 不同频偏估计算法的精度对比Tab.3 Accuracy comparison among different algorithms

7 结论

本文主要针对星载AIS信号频偏估计算法进行研究，与文献不同的是本算法不需先验信息且估计范围扩大了。从实际出发，基于FFT的算法，利用接收信号构造辅助序列确定频偏正负号，使频偏估计范围从(-1/(4Tb),1/(4Tb))变为(-1/(2Tb),1/(2Tb))，且依然具有很高的估计性能，使改进算法能够满足星载AIS信号大的多普勒频偏的需要。仿真和实验分析表明，本文改进算法不仅在理论仿真中具有良好的性能，对实际信号的估计也能达到较高的估计精度，且算法简单、易于实现，用于星载AIS系统是完全可行的。下一步工作的重点是从实用性出发，研究本文算法在应用中的性能。

[1] COLAVOLPE G,FOGGI T,UGOLINI A,et al.A highly efficient receiver for satellite-based automatic identification system signal detection[J].International Journal of Satellite Communications & Networking,2016,34(1):57-73.

[2] CLAZZER F,LáZARO F,PLASS S. Enhanced AIS receiver design for satellite reception[J].Ceas Space Journal,2016,8(4):1-12.

[3] LAN W,ZHANG T,GUO M,et al.A pipelined synchronization approach for satellite-based automatic identification system[C]//Proceedings of 2016 IEEE International Conference on Communications. Kuala Lumpur,Malaysia:IEEE,2016:1-6. [4] 陈利虎,陈小前,赵勇,等.天拓一号星载自动识别系统设计与在轨应用[J].国防科技大学学报,2015(1):65-69.

CHEN Lihu,CHEN Xiaoqian,ZHAO Yong,et al.Design and on-orbit application of TT-1 satellite-based automatic identification system[J].Journal of National University of Defense Technology,2015(1):65-69.(in Chinese)

[5] KAY S. A fast and accurate single frequency estimator[J].IEEE Transactions on Acoustics Speech & Signal Processing,1989,37(12):1987-1990.

[6] MA S X,LIU X J,MENG X. Data-aided parameters estimation of satellite-based AIS signals[J].Advanced Materials Research,2013,816-817:862-865.

[7] MORELLI M,MENGALI U. Joint frequency and timing recovery for MSK-type modulation[J].IEEE Transactions on Communications,2002,47(6):938-946．

[8] PENG H,LI J,GE L. Non-data-aided carrier frequency offset estimation of GMSK signals in burst mode transmission[C]//Proceedings of 2003 IEEE International Conference on Acoustics,Speech,and Signal Processing (ICASSP'03). Hong Kong:IEEE,2003:IV-576-9.

[9] MA S,GUO X. Frequency estimation of satellite-based automatic identification system signals[J].Journal of Computational Methods in Sciences & Engineering,2016,16(1):29-37.

[10] 刘琛. 星载AIS接收机中同步算法的研究[D].天津:天津理工大学,2016:42-46.

LIU Chen. Study on synchronization algorithms in the satellite-based AIS receiver[D].Tianjin:Tianjin University of Technology,2016:42-46. (in Chinese)

FrequencyEstimationofSatellite-basedAISSignals

MA Shexiang1,CHEN Ming1,MENG Xin2,WANG Junfeng1

(1.School of Electrical and Electronic Engineering,Tianjin University of Technology,Tianjin 300384,China; 2.Maritime College,Tianjin University of Technology,Tianjin 300384,China)

In a satellite-based automatic identification system(AIS),demodulation of signal is affected by serious Doppler frequency offset,while the traditional frequency estimation algorithm based on fast Fourier transform(FFT) can not satisfy the need.To solve the problem,an improved self-correlation-FFT algorithm is proposed. The sign of frequency offset is determined by auxiliary function. The improved algorithm is obtained on the basis of frequency offset estimation algorithm based on FFT and sign of frequency offset,and it enlarges the frequency offset estimation range and realizes the large Doppler frequency offset estimation. The simulation and experimental results show that the frequency offset estimation range of the improved algorithm is twice times of the original. The improved algorithm,with high estimation precision,is simple and easy to implement and its estimated performance is very close to the modified Cramer-Rao bound(CRB).

satellite-based automatic identification system(AIS);frequency offset estimation;large Doppler frequency offset;fast Fourier transform(FFT)

10.3969/j.issn.1001-893x.2017.12.007

马社祥，陈明，孟鑫，等.星载AIS信号的频偏估计[J].电讯技术，2017,57(12):1388-1393.[MA Shexiang,CHEN Ming,MENG Xin,et al.Frequency estimation of satellite-based AIS signals[J].Telecommunication Engineering,2017,57(12):1388-1393.]

2017-04-27；

2017-07-14

date:2017-04-27；Revised date：2017-07-14

国家自然科学基金资助项目(61371108)；天津市高等学校科技发展基金计划项目(20140706，20140707)

bjcmcy@163.comCorrespondingauthorbjcmcy@163.com

TN911

1001-893X(2017)12-1388-06