一种咬尾双二进制Turbo码并行译码方案*

2017-12-20

电讯技术 2017年12期

(重庆邮电大学通信核心芯片、协议及系统应用创新团队，重庆400065)

王琼，王伦**，杨太海

(重庆邮电大学通信核心芯片、协议及系统应用创新团队，重庆400065)

针对双二进制Turbo译码使用并行、滑动窗联合译码技术时，其咬尾的编码构造和窗分割导致边界状态值难以获取的问题，提出了一种新咬尾Turbo码并行、滑动窗译码方案——扩展交叠方案。该方案采用了边界状态盲估计和滑动窗状态回溯两种新译码技术。相比于传统的边界状态度量传播方法(又称迭代法)，新方法一方面提高了边界状态度量的准确性，从而加快了译码收敛速度，一定程度上减小了高信噪比下的性能损失；另一方面避免了存储前一次译码的迭代度量值，更有利于硬件设计。仿真表明，新方案在64左右的中等窗长下即可消除并行和滑动窗影响，逼近原始无并行无滑动窗译码的性能，且窗长越小，其相较传统迭代法带来的译码性能增益就越明显。该方案具有较好的实用性和应用价值，可以满足5G的高速率、低时延和低存储的数据传输要求。

双二进制Turbo码；滑动窗译码；并行译码；咬尾码

1 引言

Turbo码自1993年提出以来[1]，便因其接近香农限的译码性能受到广泛关注，也因此成为了第四代移动通信(Long Term Evolution,LTE)的物理层关键技术之一。随着虚拟现实、无人机和无人驾驶等技术的发展，人们对通信数据吞吐率的要求越来越高，带来的是对物理层编码技术更为严苛的要求。双二进制Turbo码的提出使得Turbo码的性能进一步提升[2]，是一种十分理想的未来高速率数据通信的信道编码技术，能很好地为上述新技术的发展提供技术支持。目前，双二进制Turbo码(Turbo 2.0)还被提为5G NR的候选编码技术之一，有着十分重要的研究价值。

双二进制Turbo码的译码多采用基于外信息迭代交换的经典BCJR译码算法[3]，如MAP (Maximum A Posteriori)算法，这类算法普遍具有译码复杂度高、时延大、储存空间占用多的特点，非常不利于工程应用。为此，基于硬件结构的多数据块并行和滑动窗译码技术的发展，相比算法优化而言更为直接有效地解决了译码时延和存储消耗问题。

Turbo码本质上是卷积码，为避免“尾效应”产生，需要让编码器状态循环。Turbo编码器使用两个分量编码器，且它们之间存在交织器阻隔，要想让两个分量编码器都实现状态循环一直是Turbo编码器设计的一个难点。LTE的二进制Turbo编码器采用12个尾比特来归零尾状态，会降低信道的带宽利用率。对于双二进制Turbo码，考虑其结构特点，通常采用文献[4]提出的咬尾Turbo码来实现状态循环，但带来了译码端难以获取准确的边界状态的新问题。特别是在使用并行和滑动窗技术之后，窗边界状态的未知使得各状态度量的计算准确度降低。文献[5]提出了用交叠法来获取状态度量估计以实现传统Turbo码的并行译码，遗憾的是该方法基于数据块的首末两端状态为零的迫零编码结构，不能应用于咬尾Turbo码。文献[6]提出了用前一次迭代的度量值作为下一次迭代的初始值的边界度量传播法(以下简称迭代法)，然而此方法受限于码长，使用并行和滑动窗技术之后，因单个滑动窗的长度受限，使得该算法收敛速度较慢，必须作出译码性能或译码时间复杂度的妥协。

基于上述问题，为满足低时延和低存储的要求，提高双二进制Turbo码并行和滑动窗联合译码性能，本文提出了一种新的双二进制Turbo码高速译码方案，即适应于咬尾双二进制Turbo码的扩展交叠方案，并通过仿真验证了其具有较好的实用性和应用价值。

2 双二进制Turbo码

不同于传统二进制Turbo码，双二进制Turbo码得益于符号级的编码、交织结构和状态咬尾的卷积编码器，体现出许多优势[7]：一是减小了交织深度，交织器效率更高；二是无需传输尾比特，带宽利用率更大；三是环形结构的网格编码对于每个信息比特有同样的保护，不会产生边界效应，降低了“误码平层”。此外，一些学者还对其距离谱进行了计算和研究[8]，从更深的理论上揭示了双二进制Turbo码的结构优势。

2.1 双二进制Turbo码咬尾处理

将双二进制Turbo码进行咬尾处理，能使其状态循环，从而保证边界比特与中间比特受保护程度相同。本文采用如下咬尾处理过程：

Step1 将RSC编码器初始化为全0状态，即S0=[s1,s2,s3]=[0,0,0]。

Step2 将整个FEC块经分量编码器编码(此次的输出不使用)，得到编码后寄存器的最终状态为SN。

Step3 由公式

(1)

矩阵M与具体的编码结构有关:

M=[I-GN]-1。

(2)

式中：I为单位矩阵；N为码字长度；G为编码器生成矩阵，取决于分量编码器的具体结构，通常都采用递归系统卷积码(Recursive Systematic Convolution code,RSC)。

以图1所示电力线通信HomePlug协议中的双二进制Turbo编码器为例[9]，G矩阵可表示为

(3)

图1 分量编码器结构图Fig.1 Structure diagram of component encoder

因G7=I，可将式(1)所示预编码末状态与咬尾状态的对应关系制作成表格，通过预编码末状态和编码码字长度可容易地查得咬尾状态。表1列出了图2所示编码结构下各码字长度的咬尾状态。

表1 循环状态查询表Tab.1 The loop state table

需要说明的是，经过咬尾处理后两个RSC编码器的咬尾状态并不相同，且接收端无法获取该状态，这也是双二进制译码的技术难点，亦是本文要解决的问题。

2.2 双二进制Turbo码译码原理

双二进制Turbo码的译码结构基于外信息交换的迭代译码。两个分量译码器通过交织(解交织)器相连，其中一个译码器的外信息作为另一个译码器的先验信息实现迭代译码。最后，将其中一个分量译码器硬判决即得到发送信息序列的估计值。两译码器间的信息交换使得译码结果最终收敛于最大似然译码。分量译码器的实现算法较多，但考虑到性能、硬件实现和时间复杂度的折中，本文都将采用MAX-Log-MAP作为译码算法。

双二进制Turbo码的MAX-Log-MAP译码由似然比进行比特判决，似然比计算公式如下:

(4)

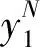
(1)分支度量

计算方式如下：

(5)

(2)前向状态度量

按如下递推公式计算：

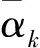
(6)

(3)后向状态度量

按如下递推公式计算：

(7)

最后，可得到传递给另一个译码器的外信息：

Le(uk)=L(uk)-La(uk)-

(8)

式中：La(uk)为先验信息，取上一个译码器的输出外信息；s′为上一时刻状态；s为当前时刻状态。前向状态度量向后迭代，需要在前端进行状态初始化；后向状态度量向前迭代，则要设置后端的初始化状态，获取的边界初始状态准确与否是译码算法性能差异的关键。

改进的分量译码器的计算过程如图3所示：先根据式(6)计算整个数据块的前向度量(图中α)并存储，再读取储存的前向度量和通过式(7)计算的后向度量(图中β)值逐比特代入式(4)即可计算似然比(LLR)，最后由式(8)计算外信息并经过交织或解交织后送入下一个分量译码器继续迭代译码。采用这种译码结构的译码器避免了存储后向度量，可节约一半的存储空间。为避免系统过大的空间复杂度开销，以下所有仿真都将采用这种改进的译码方法。

图2 分量译码器译码流程Fig.2 Decoding process of component decoder

2.3 双二进制并行、滑动窗译码

本文所述的并行分块处理方法同文献[10]，具体的分块处理过程这里不再详述。为保证译码效率，通常高性能译码器都采用硬件直接实现。上述的改进方法仍然需要将整个FEC块的前向度量都存储下来才能译码，如1 024的块长，8个状态以6 bit方式存储，双二进制译码就需要24 576 bit的空间，这对硬件设计来说是不能忍受的。而并行、滑动窗译码技术的应用分别实现了高速率和低存储译码，大大降低了译码时延和硬件资源消耗，特别是与双二进制Turbo结合的并行、滑动窗译码将是未来5G物理层编码技术的利器。

然而,数据的分割和咬尾技术致使边界状态的未知很大程度上影响了译码性能。目前的译码器多采用文献[6]提出的迭代法来估计边界状态。原理是：将本次迭代的前向和后向度量的估计值存储下来作为下一次迭代的初始值，码字边界利用循环结构特点进行迭代状态传播。本文仿真表明，该算法比起原始非并行译码有较大的性能损失。

3 本文新译码方案

为了提高并行、滑动窗译码性能，本文提出了一种新并行译码方案，既体现了良好性能优势，又减少了迭代存储器的数量。新并行和滑动窗方案主要特点一是边界状态盲估计，即复制首尾少量数据作为训练序列，通过预计算来得到边界状态的盲估计值；二是滑动窗状态回溯，即在滑动窗中用前向度量反向初始化后向度量值，再回溯修正得到后向度量的估计。可使后向度量也近似参与循环迭代，得到的状态估计值具有更好的准确性。新方法使得复制的数据参与计算，仅仅牺牲了少量的时间复杂度，却带来了较大的译码性能提升，又避免了存储后向度量值的硬件消耗。

3.1 边界状态盲估计

并行译码的各并行块之间采用不同译码器，数据之间的联系被完全截断，因此并行块的边界状态的准确性对性能有直接影响。传统的状态传播的迭代法无法满足性能要求，因而本文提出使用训练序列边界状态盲估计的方法，再结合传统迭代法可以最大限度地减小估计误差。

边界状态估计的原理基于卷积码的MAP译码是一种循环网格译码方法，译码性能与译码起始点无关，即可以从任何分支开始译码。随着分支的增长，状态也就逐渐准确。正是利用卷积网格译码的这个性质，我们可以使用训练序列来盲估计初始译码状态，文献[4]指出训练序列的长度为约束长度的6倍就足够了。由于本文引入了迭代法联合估计，原本的初始状态就较为准确，因此可以适当减小训练序列的长度。结合图3，本文所提双二进制并行译码的译码步骤描述如下：

Step1 利用咬尾卷积码首尾状态相同的性质，将处于码字前端的L个比特复制到尾部作为训练序列用于初始状态的预估计值。

Step2 如图中实线箭头所示，将上一次迭代时该处的状态度量存储下来作为预计算的初值。

Step3 初始化状态为零，利用训练序列盲估计正式译码的初始状态。

Step4 以上一步骤估计的初始状态进行正式译码。

以上是后向度量的估计过程，前向度量的估计过程和后向度量的估计过程原理相同，只是复制的数据是从尾部复制到头部。

图3 边界状态盲估计Fig.3 Blind estimation of boundary state

3.2 滑动窗状态回溯

滑动窗的引入很大程度上减小了译码器的存储开销，但传统迭代法的使用又增加了存储前一次迭代度量值的开销。对于较大码长的码字而言，窗的数量会比较多，这部分开销相应的增大。并且不同码字长度需要的存储大小不同，还不利于硬件电路的设计，常常会以最大码长来分配存储，造成一定的资源浪费。

可以推导在双二进制Turbo码的译码过程中的前向度量和后向度量。根据马尔科夫性质，有

(9)

(10)

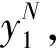
lαk(s)≈kβk(s)≈P(sk) 。

(11)

保持线性关系，但并不是准确值。可采用类似文献[11]的存储方式以提高状态传递的准确性，最终得到

(12)

式中：

图4所示为改进的滑动窗方案。由于前向度量值在滑动窗之间相继传播而不会被分割，其状态估计值较后向度量更为准确，因此本文探究了用αk(s)值初始化βk(s)值。根据以上的推导，形如式(12)的初始化方法可行，因此如图中所示在交叠末端进行状态传播对后向度量初始化。此外，滑动窗之间还有长度为WL的较短(选用的窗交叠WL小于并行块的盲估计序列L)窗交叠序列用于回溯辅助修正，使得正式译码时获得的度量值更为准确，综合译码性能更佳。显然，该方案不需要存储上一次迭代的中间状态，在码长较长时能很大程度地节省存储开销。同时，这种处理方式对任意码字长度的处理过程相同，也利于译码器的硬件设计(不会因最大存储分配而浪费硬件资源)。

图4 滑动窗状态回溯Fig.4 State backtracking of sliding window

4 仿真和性能分析

为验证本文算法性能，针对无线应用场景，在AWGN信道进行了对比仿真，均采用图1所示的编码结构。仿真在Turbo编译码模块和等效比特信道下进行，非当前仿真变量的其他任何参数都采用表2给出的默认参数(为保证无线通信要求，这些参数综合参考LTE和HomePlug AV协议，仿真次数要求达到误帧率在10-3左右)。

表2 默认仿真参数 Tab.2 Default simulation parameters

图5对4种算法分别在窗长为32和64下进行了仿真，结果表明，双二进制Turbo码的迭代并行方案的性能最差，且该算法对窗长的依赖更为明显。这是由于迭代方案要经多次迭代才能形成一个译码循环，译码收敛速度慢，致使收敛需要更多的迭代次数；又考虑到复杂度原因，不能靠增加迭代次数来提高性能。由此看来，这个目前应用较广的方案并不佳。迭代加交叠的译码方法在所有信噪比下都比较接近原始非并行方案，高信噪比下甚至会超过无并行的原始方案，是在性能上最为理想的译码方案。这是由于该方法使用大量的交叠数据使得实际译码码长变长，带来了较大的性能增益。同时，迭代方法的引入也使得译码器状态循环从而避免了截断损失，但其消耗的时间和存储资源是最多的。该方案仅适合那些对性能要求较高而资源相对宽裕的通信场景。

(a) 窗长为32的性能曲线

(b) 窗长为64的性能曲线图5 4种算法性能对比Fig.5 Performance comparison among the four algorithms

本文新方案在误帧性能上稍逊于非并行的原始方案，且差距很小。随着窗长的增大逐渐逼近于非并行的原始方案，仿真结果表明在窗长为64的时候性能差距已基本可以忽略。新方案比起迭代方案有较大的性能增益，窗长32且按表2设置默认参数时大约是0.05 dB，但窗长越小、交叠序列越长，性能增益就会越明显。综合考虑各方案的存储开销和硬件设计要求，新方案很好地实现了在性能、复杂度和存储开销等各方面的折中，具有较好的实用性和有效性。

图6所示为新方案在训练序列长度为约束长度3～6倍下的仿真对比，可见在4～6倍约束长度下都不会有太大性能损失，这得益于新方法结合了交叠和迭代的优点，在性能损失可接受的情况下可尽可能地减少存储消耗。序列长度大于约束长度4倍以后对性能的提升幅度很小，所以采用4倍约束长度最佳。

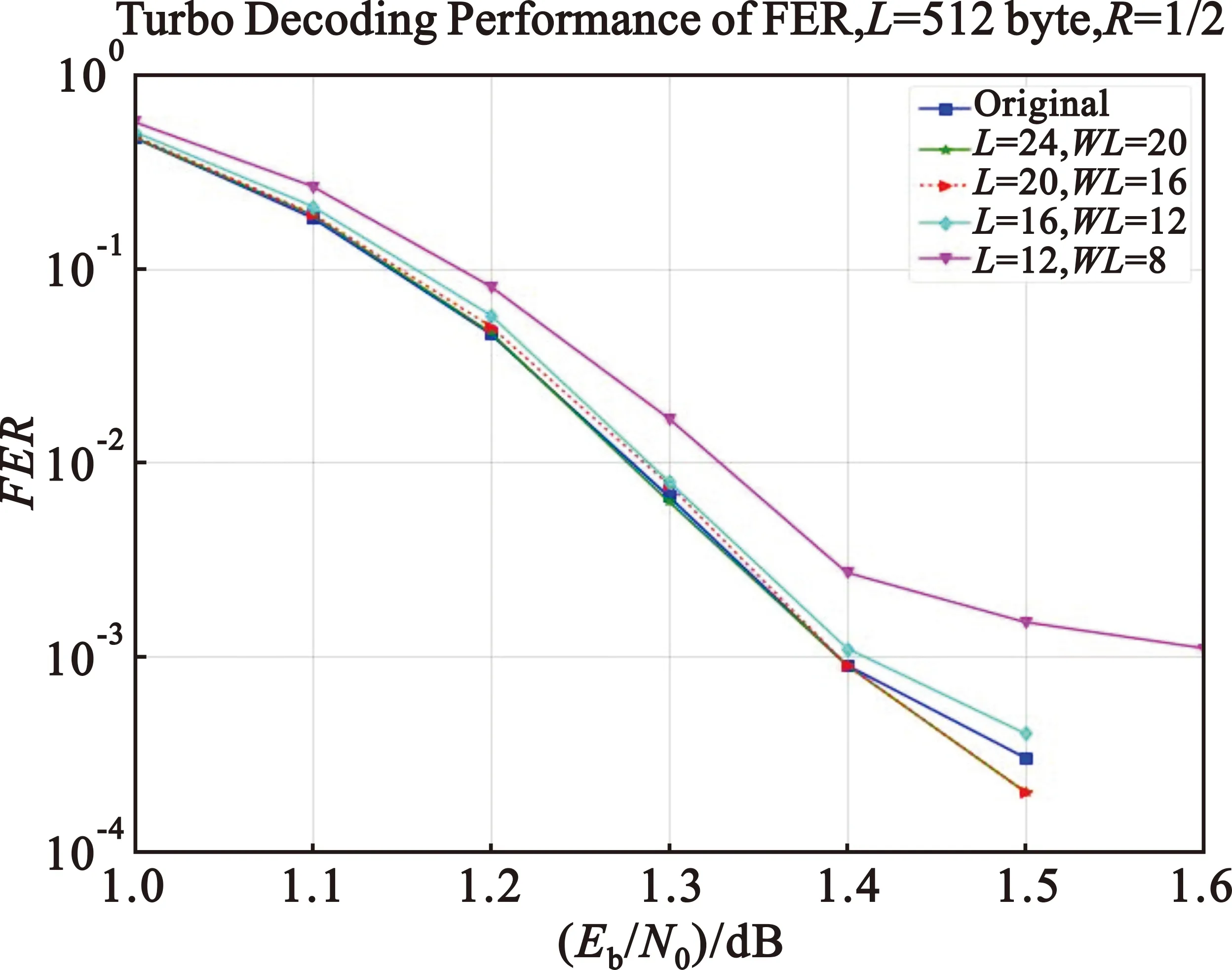
图6 各训练序列长度下的性能对比Fig.6 Performance comparison under different length of training sequences

图7为新方案在不同的并行度下的译码性能曲线，表明了并行度对于算法的性能影响很小(不到0.02 dB)。仿真表明，并行度为16的译码结果反而是最好的，这实际上与本文中使用的边界状态盲估计采用的是最大化保证性能的算法相吻合。由此可见，本文新方案相比LTE的Turbo可以支持更大的并行度，即实现更小的译码时延，完全可以满足5G中10 Gbit/s的峰值速率和毫秒级的时延要求。

图7 各并行度下的性能对比Fig.7 Performance comparison under different degrees of parallelism

5 结束语

本文在分析双二进制Turbo码特征的基础上，提出了一种改进的双二进制并行和滑动窗译码方案。新并行方案改进了传统迭代译码方法，提出了边界状态的盲估计方法，给译码带来了较大增益；同时使用了回溯的新滑动窗估计方法，用前向度量初始化后向度量来减小存储和方便硬件设计。新方法使用的这两项关键技术提高了边缘状态的准确性，在迭代译码中具有更快速的收敛速度。在仿真迭代次数有限的情况下，比起文献[6]中的迭代法更加逼近于最大似然译码，从而体现出了更好的译码性能。仿真表明，新方案相比传统双二进制边界度量传播译码方法有较大性能提升，对窗长和训练序列的长度依赖性也更弱：在中等窗长下便可以逼近非并行原始译码方案，并且使用不超过4倍约束长度的训练序列就能保证较好的性能。当然也有一些代价，本文所提新方案在复杂度上比起迭代方案略有牺牲，主要是由窗及译码器间的交叠数据引起的，但上述的改进译码方法和滑动窗回溯等技术的使用已对此有较大的改善，更低时间复杂度的译码方法还需进一步研究，例如部分学者对其停止条件的研究[12]就是一个比较有前景的方向。综上所述，新方案是一种综合较优的双二进制并行和滑动窗译码方案，可以很好地满足未来5G高速率、低时延的无线通信需求。

[1] BERROU C,GLAVIEUX A,THITIMAISHIMA P. Near Shannon limit error-correcting coding and decoding:Turbo-codes(1)[C]//Proceedings of 1993 IEEE International Conference on Communications.Ottawa，Canada:IEEE，1993:1064-1070．

[2] BERROU C,JEZEQUEL M. Non-binary convolutional codes for turbo coding[J].Electronics Letters,1999,35(1):39-40.

[3] BAHL L,COCKE J,JELINEK F,et al.Optimal decoding of linear codes for minimizing symbol error rate[J].IEEE Transactions on Information Theory,1974,20(2):284-287.

[4] SUN J,TAKESHITAO Y. Extended tail-biting schemes for turbo codes[J].IEEE Communications Letters,2005,9(3):252-254.

[5] VITERBI A J. An intuitive justification and a simplified implementation of the MAP decoder for convolutional codes[J].IEEE Journal on Selected Areas in Communications,1998,16(2):260-264.

[6] DIELISSEN J,HUISKEN J. State vector reduction for initialization of sliding windows MAP[C]//Proceedings of 2nd International Symposium on Turbo Codes & Related Topics. Brest,France:IEEE,2000:387-390.

[7] BERROU C,JEZEQUEL M,DOUILLARD C,et al.The advantages of non-binary Turbo codes[C]//Proceedings of 2001 IEEE Information Theory Workshop. Cairns,Queensland,Australia:IEEE,2001:61-63.

[8] DENG J,PENG Y,ZHAO H. Distance spectrum calculation method for double binary Turbo codes[C]//Proceedings of 2017 International Conference on Recent Advances in Signal Processing,Telecommunications & Computing (SigTelCom). Da Nang,Vietnam:IEEE,2017:98-102.

[9] HomePlug Powerline Alliance.HomePlug AV specification version 1.1[S].[S.l.]:HomePlug Powerline Alliance,2007:36-37.

[10] 任德锋,葛建华,宫丰奎,等.新颖的低延迟并行Turbo译码方案[J].通信学报,2011,32(6):38-44.

REN Defeng,GE Jianhua,GONG Fengkui,et al.Novel low-delay scheme for parallel Turbo decoding[J].Journal on Communications,2011,32(6):38-44.(in Chinese)[11] WANG L,YANG H,YANG H. A novel method for parallel decoding of turbo codes[C]//Proceedings of the 4th IEEE International Conference on Circuits and Systems for Communications. Shanghai:IEEE,2008:768-772.

[12] GUERRIERI L,VERONESI D,BISAGLIA P. Stopping rules for duo-binary Turbo codes and application to HomePlug AV[C]//Proceedings of 2008 IEEE Global Telecommunications Conference(GLOBECOM).New Orleans,LO,USA:IEEE,2008:1-5.

AParallelDecodingSchemeforTail-bitingDuo-binaryTurboCodes

WANG Qiong，WANG Lun，YANG Taihai

(Communication Core Chip,Protocols and Application Innovation Team, Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

When the tail-biting duo-binary Turbo codes use parallel and sliding window joint decoding technology,the tail-biting encoding structure and the window segmentation lead to the difficulty of obtaining the boundary state metric. To solve the problem,this paper presents a novel parallel and sliding window decoding scheme called extended overlap scheme. The new scheme utilizes two new decoding techniques:the boundary state blind estimation technique and the sliding window state backtracking technique. Compared with the traditional Boundary State Metric Propagation(BSMP) method(also called the iterative method),on the one hand,the new method improves the accuracy of the boundary state metric,thus speeding up the decoding convergence,and reducing the performance loss at a high signal-to-noise ratio(SNR) to some extent. On the other hand,it helps to avoid storing the state metric of the last iteration,which is more conducive to the hardware design. Simulation results show that this method can eliminate the effects of parallel and sliding window,approximating the performance of the original non-parallel and non-sliding window decoding method at the medium window length about 64. And the smaller the window length is,the more obvious the decoding performance gain is than the traditional iteration method. Therefore,this scheme has better practicability and application value,which satisfies the current high speed,low latency and low storage data transmission requirements of 5G.

duo-binary Turbo code;slipping window decoding;parallel decoding;tail-biting code

10.3969/j.issn.1001-893x.2017.12.001

王琼，王伦，杨太海.一种咬尾双二进制Turbo码并行译码方案[J].电讯技术，2017,57(12):1349-1355.[WANG Qiong，WANG Lun，YANG Taihai.A parallel decoding scheme for tail-biting duo-binary Turbo codes[J].Telecommunication Engineering,2017,57(12):1349-1355.]

2017-07-04；

2017-08-24

date:2017-07-04；Revised date：2017-08-24

国家科技重大专项(2016ZX03002010-003)

iswanglun@qq.comCorrespondingauthoriswanglun@qq.com

TN911.22

1001-893X(2017)12-1349-07