基于数字积分算法的电子式电流互感器传变特性
2017-12-20张杰恺李辉邓吉利贺胜曹林何蓓
张杰恺,李辉,邓吉利,贺胜,曹林,何蓓
(1.国网重庆江北供电公司,重庆401123;2.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆400044;3.国网重庆市电力公司,重庆401123)
0 引 言
Rogowski线圈电子式电流互感器不含铁心,消除了磁饱和、铁磁谐振问题,具有频率响应范围宽,暂态响应范围大,测量精度高等优点[1]。电子式电流互感器作为系统信息采集的主要设备,将逐渐取代传统的电磁式互感器,在电力系统的电能计量、测量和继电保护中发挥重要作用[2]。积分环节作为Rogowski线圈电子式电流互感器的关键环节之一,不同厂家制作上存在差异,使得相差比差不同,影响电能计量、测量和继电保护的准确性。此外,积分环节往往导致“拖尾效应”,当电网中电流突变,富含直流分量或谐波分量时,不同积分算法的动态响应能力可能不同。因此全面比较研究不同积分算法下电子式互感器的传变特性,对电子式互感器的优化设计和运行监测以及适应性保护的研究都具有重要现实意义。
目前,现有学者对电子式电流互感器的积分环节提出了较多不同算法,如模拟积分[3]、数字积分矩形算法[4]、梯形算法[5]、Simpson算法[6]、双线性变换算法[7-8]和 Al-Alaoui[9]算法等。由于模拟器件受时漂和温漂的影响较大,在实际中很少采用。文献[5]设计了基于STM32F103梯形算法的数字积分器,但并没有与其他积分算法进行比较与分析。文献[6]研究了3种常用的矩形算法、梯形算法、Simpson算法的电子式互感器特性,但是文献仅涉及了不同积分算法幅频特性的比较,没有深入分析含不同积分算法的互感器频带特性,对其动态响应能力的比较没有涉及。文献[7]研究了双线性变换算法的幅频特性和谐波特性,但是仅从精度上与其它积分算法进行了比较。文献[10]设计了对Rogowski线圈电流互感器的精确度、饱和特性、频率特性和暂态特性的测试方案,但是文中仅涉及互感器等效电路本身,没有考虑数字积分环节对其传变特性的影响。综上所述,对现有不同积分算法的电子式电流互感器整体的频带特性还需要完善,对其动态响应能力的比较还有待深入研究。
本文以Rogowski线圈电子式电流互感器为例,对常用的矩形、梯形、Simpson和双线性变换积分算法进行比较分析,全面评估不同积分算法可能对其传变特性的影响。首先,分别获取Rogowski线圈等效电路和积分算法的传递函数;其次,对各个环节幅频和相频特性进行分析,获取并比较了含不同积分算法的电子式互感器整体的频带特性;最后,以某实际110 kV变电站用电子式电流互感器参数为研究对象进行分析,针对稳态和信号突变的动态情况,对含不同积分算法的电子式互感器传变特性进行仿真。
1 电子式电流互感器的建模
所采用的Rogowski线圈电子式电流互感器的结构如图1所示。被测电流经Rogowski线圈输出微分后的信号,再通过A/D采样和数字积分器输出与被测电流成一定比例的信号,最后通过合并单元作进一步处理。

图1 Rogowski线圈电子式电流互感器结构Fig.1 Structure of Rogowski coil electronic current transformers
1.1 Rogowski线圈的等效电路
Rogowski线圈的等效电路如图2所示,其中L0、R0、C0分别为Rogowski线圈的自感、内阻和杂散电容,Rs为取样电阻,M为Rogowski线圈的互感系数,e(t)为 Rogowski线圈的感应电势,u0(t)为 Rogowski线圈的输出电压,I为被测电流。
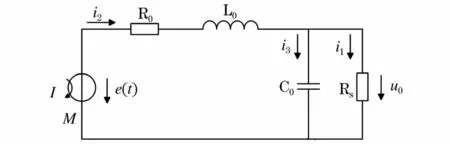
图2 Rogowski线圈的等效电路图Fig.2 Equivalent circuit diagram of Rogowski coil
通过基本电路分析和拉氏变换可得到Rogowski线圈的传递函数:
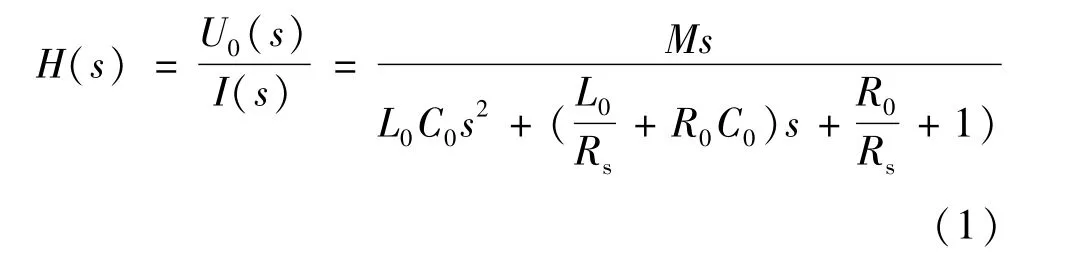
用于电力系统的Rogowski线圈电子式电流互感器常工作于外积分方式,此时Rogowski线圈的输出电压与被测电流满足微分关系,即:
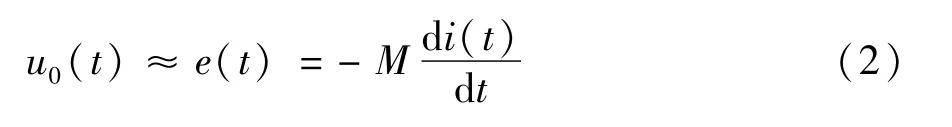
由上式可知,为了还原被测电流,就需要对输出电压进行积分。
1.2 不同积分算法的传递函数
数字积分通过软件算法来实现,且基本不受温度和其他因素的影响,因而得到广泛的应用。常用的数字积分算法主要有矩形算法、梯形算法和Simpson算法。根据它们的z传递函数,依次得到其递推公式如下。
矩形算法:
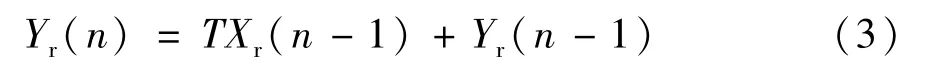
梯形算法:
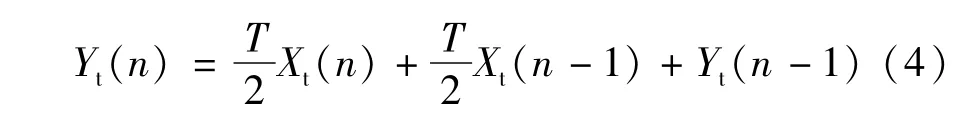
Simpson算法:
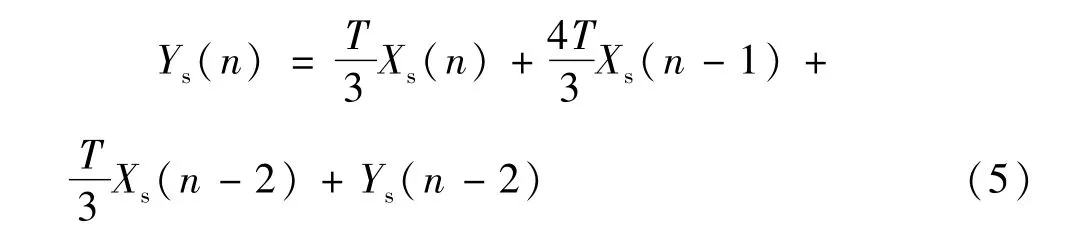
式中 T为采样间隔,n表示采样时刻,X(n)与Y(n)分别表示n时刻积分环节的输入和输出,下标r、t和s分别表示矩形算法、梯形算法和Simpson算法。
为了抑制低频信号的干扰,最近文献提出了双线性变换积分算法[7-8]。其主要思想是:使s平面的虚轴映射为z平面的单位圆,从而实现模拟域到数字域的映射。s与z的关系公式为:

利用双线性变换,将公式(6)代入某模拟积分公式中:
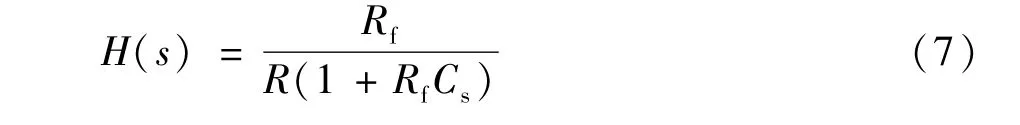
并得到对应的递推公式为:
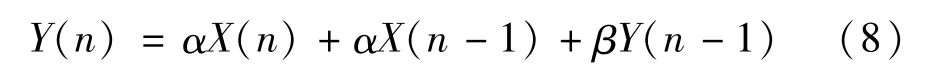
式中 α=-TRf/(TR+2RRfC),β=-(TR-2RRfC)/(TR+2RRfC),R、C和Rf分别为对应模拟积分的电阻、电容和反馈电阻值。
为了全面分析比较不同积分算法的电子式电流互感器的传变特性,本文采用式(3)~式(5)和式(8)的数字积分传递函数对Rogowski线圈电子式电流互感器进行频带特性以及不同信号源下传变特性的研究。
2 含积分环节的Rogowski线圈互感器的频带特性
2.1 Rogowski线圈环节的频带特性
按照前述Rogowski线圈的等效电路和第3节的仿真参数可得Rogowski线圈环节频带特性,其Bode图如图3所示。
从相频特性可以看出,Rogowski线圈的输出电压与被测电流约有90°的相位差,存在微分关系。
2.2 不同积分算法的频带特性
按照4种数字积分的传递函数和第3节的仿真参数,可得4种积分算法的频带特性,其Bode图如图4所示。
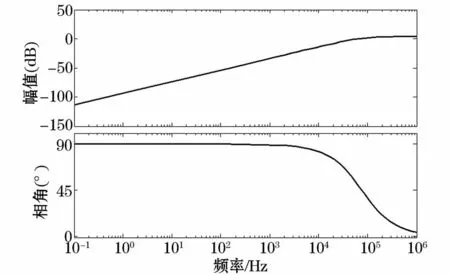
图3 Rogowski线圈环节的Bode图Fig.3 Bode diagram of Rogowski coil
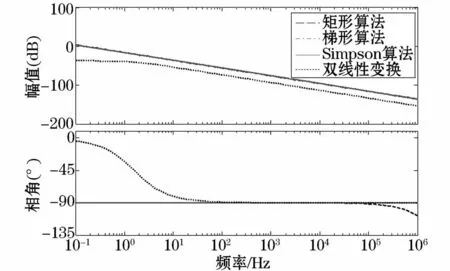
图4 4种数字积分算法的Bode图Fig.4 Bode diagram of four kinds of digital integrators
从上述幅频特性可以看出,这4种不同积分算法的对数幅频曲线斜率均为-20 dB/dec,但是它们在低频响应上存在差异,特别是双线性变换积分算法由于是根据模拟积分变换而得,因此它具有与模拟积分相类似的频带特性,即在频率f<1 Hz区域对数幅频曲线斜率为0 dB/dec,而常用的数字积分算法对数幅频曲线斜率为-20 dB/dec。
另外,从上述相频特性可以看出,这4种不同积分算法都达到了-90°的相位延迟,但是它们在低频响应和高频区域上仍然存在差异。在低频区域,采用的双线性变换积分算法的相位延迟几乎为0°,表示在低频区域,该算法丧失积分功能;在高频区域,矩形算法的相位则随着频率的增大而增大。
因此,从上述Bode图可以看出,不同数字积分在低频和高频区域存在一定的差异,其中双线性变换积分算法反映在低频方面的差异;而矩形算法反映在高频区域。
2.3 含积分环节的电子式互感器整体频带特性
基于上述4种不同积分算法的传递函数,联合Rogowski线圈环节传递函数,以及第3节的仿真参数可得含积分环节的电子式电流互感器整体传递函数的频带特性,其Bode图如图5所示。
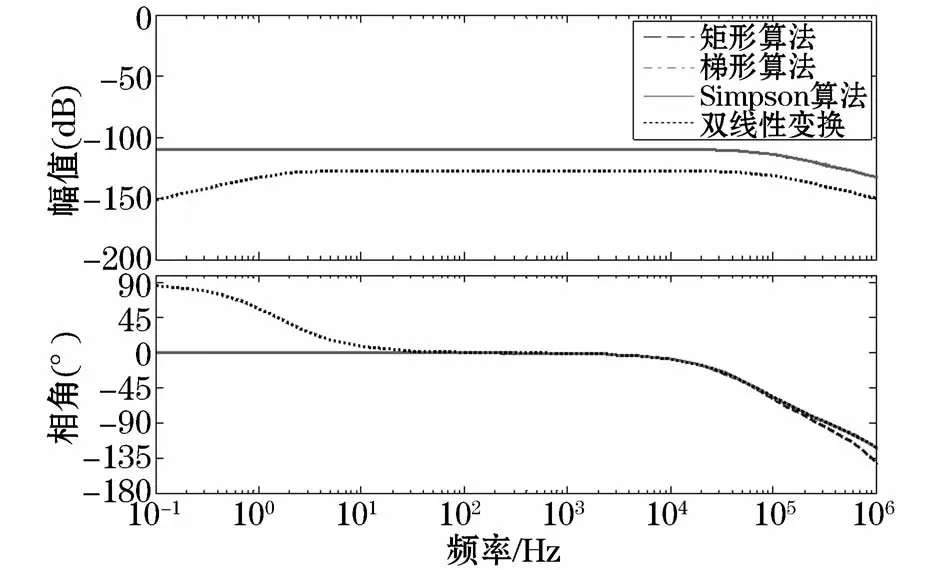
图5 含不同积分算法的电子式电流互感器整体Bode图Fig.5 Bode diagram of electronic current transformer with different integrators
从图5中可以看出,在频率10 Hz~10 kHz的范围内,4种积分算法的互感器幅频特性和相频特性表现为水平直线,可见在上述频带范围内,不同积分算法时电子式电流互感器输出信号的幅值和相位不受频率变化的影响,即能够准确地还原被测电流中的各种频率分量,频带特性较好。然而,当频率小于10 Hz时,相对其他积分算法,采用双线性变换积分算法时的还原特性会更容易受到原始信号低频分量的影响;而当频率大于10 kHz时在高频区域,上述4种积分算法的互感器输出的相位则会随着频率的增大而增大,从而很大程度上影响其还原特性。
3 仿真分析
为了较全面的分析不同积分算法Rogowski线圈电子式电流互感器传变特性及其影响,本文以实际110 kV数字化变电站中的Rogowski线圈电子式电流互感器为例,其仿真用的主要参数如下[11]:一次额定电流为I=600 A,M=3.369μH,L0=21.56 mH,R0=270Ω,C0=0.12 nF,Rs=10 kΩ,采样时间 T=0.1 ms,其中当采用双线性变换积分算法时取R=30 kΩ,C=0.1μF,Rf=1 MΩ。基于PLECS仿真平台搭建了含上述4种不同数字积分算法的Rogowski线圈电子式电流互感器的模型,下面针对稳态信号、积分初值不确定,以及信号突变或富含直流、谐波信号不同情况,对不同积分算法的互感器传变特性进行仿真。
3.1 工频稳态下的传变特性比较
现选择初始相位角为0°,频率为50 Hz,标幺值为1的额定电流 i(t)=sin(100πt)作为输入信号,4种不同积分算法的互感器输入-输出波形如图6所示。
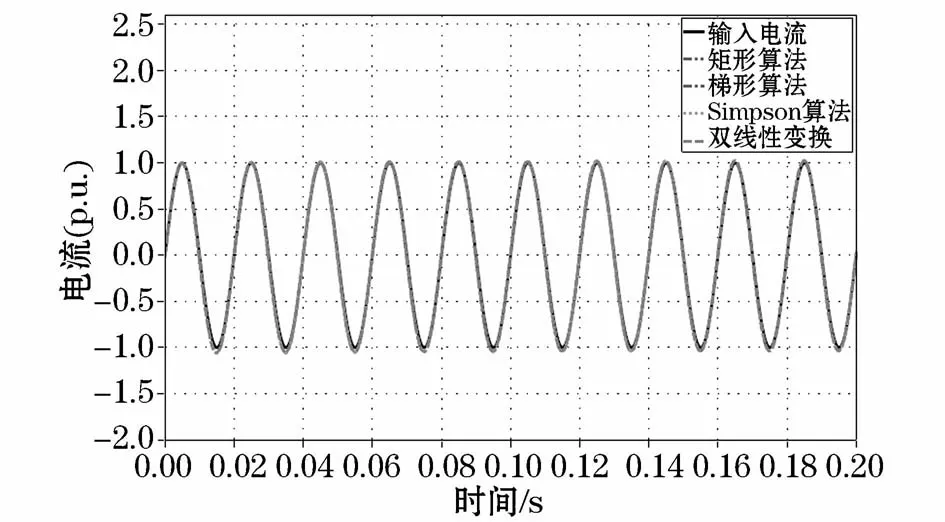
图6 稳态特性下互感器传变特性比较Fig.6 Comparisons of the transducer transfer characteristics under the steady-state input condition
从结果可以看出,4种积分算法的互感器稳态响应良好,均能较好的还原被测波形。其比差和相差如表1所示,通过表中计算结果可知,4种积分算法的电流互感器在额定电流下都能满足较高的准确度要求。
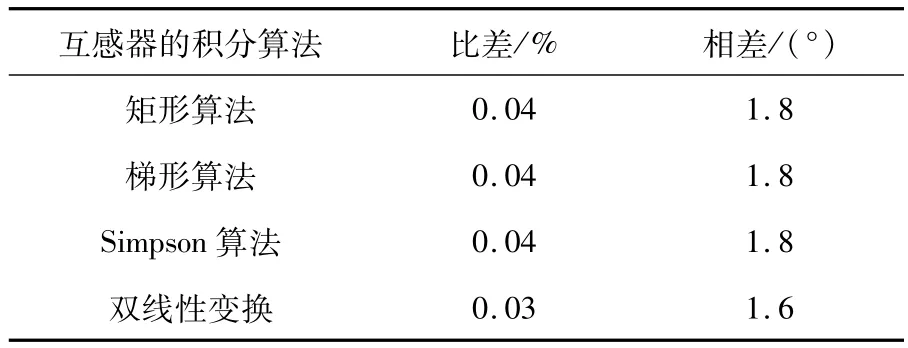
表1 额定电流下互感器的准确度Tab.1 Accuracy of transformers at rated current
3.2 积分初值不确定情况下的动态响应特性比较
由于电子式电流互感器还原被测电流需要对Rogowski线圈的输出电压进行积分处理,即:
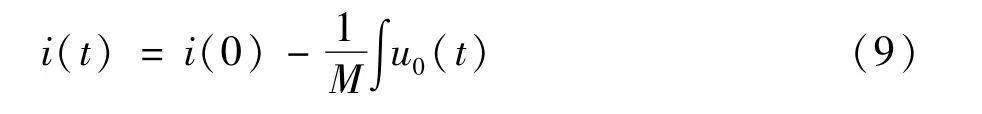
因此需要确定数字积分的初值。为了验证不同积分初值对上述积分算法的鲁棒性,现假定输入电流存在 90°初始相位,即 i(t)=sin(100πt+90°),而积分算法仍假设初值为0,图7得到了4种积分算法下Rogowski线圈电子式电流互感器传变特性。

图7 积分初值不确定下互感器传变特性比较Fig.7 Comparisons of the transducer transfer aracteristicswith the unknown initial integration points
从图7可以看出,采用双线性变换积分算法时互感器可以在较短时间内的还原输入电流,具有积分初值不确定下鲁棒性好的优点。而采用矩形算法、梯形算法和Simpson算法的互感器输出则受积分初值不确定下影响大,输出信号含有50%幅值的直流分量,导致其传变特性输出信号幅值下移50%,还原信号能力明显降低。
3.3 输入信号幅值突变下的动态响应特性比较
由于电网中的功率控制或负荷变化等各种因素下可使互感器的输入电流突然增加或者降低,为了仿真分析电流幅值突变时对不同积分算法下互感器传变特性的动态跟踪能力比较,现假定输入电流为i(t)=sin(100πt),在 t=0.044 s时刻电流幅值从 1 p.u.突变为1.5 p.u.,在t=0.104 s时刻电流幅值又从1.5 p.u.突变回1 p.u.,仿真比较4种不同积分算法时互感器动态响应情况,如图8所示。
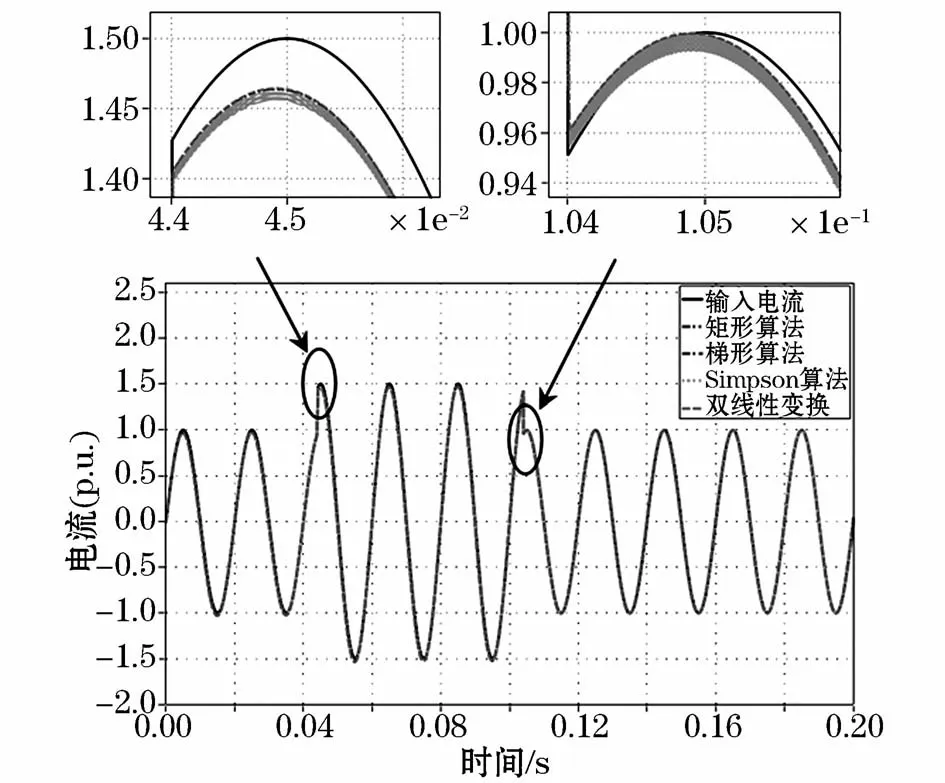
图8 输入信号幅值突变下互感器传变特性比较Fig.8 Comparisons of the transducer transfer characteristicswhen the input amplitude is changed
从图8中的仿真波形可以看出,4种不同积分算法的互感器在电流幅值突变情况下输出波形与输入波形吻合,能较好地还原输入信号。但是从其动态响应能力可以看出(观察放大波形),4种不同积分算法的互感器动态响应和幅值跟踪方面仍存在一定的差异,与其余3中积分算法比较,Simpson算法的幅值突变的跟踪响应能力较差。
3.4 输入信号富含直流分量时动态响应特性比较
当线路中发生过电压或故障时,由于电感或电容的存在,往往使得电流不能突变而导致线路中存在直流分量的情况。此外,由于Rogowski线圈输出信号弱,在外界干扰下也可能导致积分环节的输入信号中含有直流分量。为了比较分析富含直流分量时互感器传变特性,下面对Rogowski线圈输入信号和积分环节输入信号富含直流分量时的情况进行仿真,如图9所示。其中,图9(a)为输入电流i(t)=sin(100πt),在 t=0.1 s开始含有 1 p.u.衰减时间常数T=0.05 s的直流分量时传感器传变特性的仿真结果;图9(b)为假定在t=0.1 s时积分环节输入信号含10%幅值的稳定直流量干扰下传感器传变特性的仿真结果。
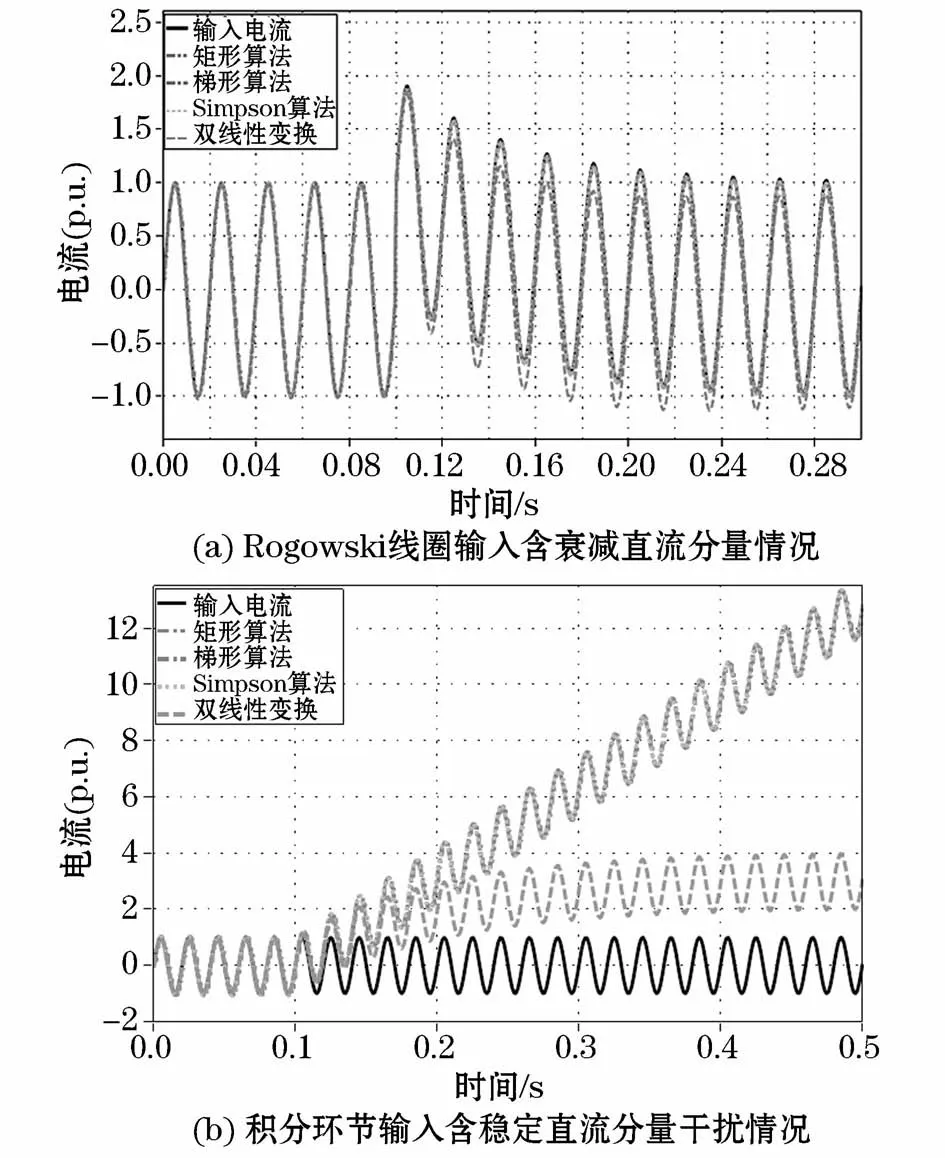
图9 含不同直流分量时互感器传变特性比较Fig.9 Comparisons of the transducer transfer characteristicswhen the input has different DC signals
从图9(a)可以看出,当Rogowski线圈输入含衰减直流分量时,不同积分算法基本上都能还原其输入信号的变化,但相比之下,采用双线性变换积分算法时还原能力相对较差。
从图9(b)可以看出,当积分环节输入含稳定直流分量干扰情况下,双线性变换积分算法受直流量干扰的影响相对较小,还原特性好,而其余3种算法受直流量干扰的影响较大,导致其互感器输出信号随着时间推移不断增大,呈现明显发散的传变特性。
3.5 输入信号富含谐波分量时动态响应特性比较
为了模拟线路中存在谐波分量时互感器的动态性能,现假定线路中存在2~13次的谐波分量,即输入电流为 i(t)=sin(100πt),并在 t=0.1 s开始输入幅值分别为 1/2、1/3、1/4、1/5、1/6、1/7、1/8、1/9、1/10、1/11、1/12和1/13的2~13次谐波分量,得到图10所示仿真波形。从图中可以看到,采用4种积分算法的互感器均能很好的还原被测电流中的低次谐波分量。

图10 含2-13次谐波分量时互感器传变特性比较Fig.10 Comparisons of the transducer transfer characteristicswhen the input has 2-13 order harmonic components
另外,当线路中电感、电容存在导致谐振可能会存在高次谐波情况,为了分析不同积分算法下互感器对线路中高次谐波分量的影响,现假定输入电流为 i(t)=sin(100πt),在 t=0.1 s开始输入频率为106Hz、幅值为0.1的高次谐波,采用不同积分算法时其互感器传变特性如图11所示。
从图中可以看出,采用上述4种积分算法的互感器还原高次谐波信号的能力都较差,这与图5中含不同积分算法时互感器整体输出的频带特性分析结果一致,即当Rogowski线圈输入信号含高次谐波分量时,上述不同积分算法并不能很好反映其输出高次谐波特性。
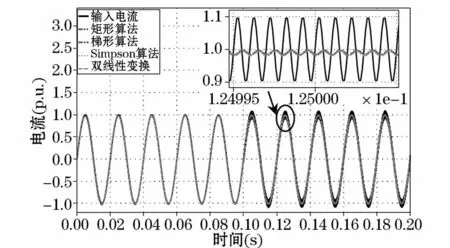
图11 含高次谐波分量时互感器传变特性比较Fig.11 Comparisons of the transducer transfer characteristicswhen the input has a high-order harmonic component
4 结束语
以Rogowski线圈电子式电流互感器为例,通过建立传递函数和仿真模型,对常用的矩形、梯形、Simpson和双线性变换积分算法下的互感器频带特性和传变特性时域仿真进行了比较分析,得到以下结论:
(1)从频带特性上和输入信号富含谐波分量时的仿真比较可以看出,在频率10 Hz~10 kHz的范围内,上述4种积分算法的电子式电流互感器幅值和相位不受频率变化的影响,即能够较准确地还原被测电流中的各种频率分量,频带特性较好,但在低频以及高频率信号下还原能力较差;
(2)从稳态特性的比较分析可以看出,4种积分算法的互感器还原输入电流的能力都较好,在额定电流下都能满足较高的准确度要求。但在积分初值不确定的情况下,采用双线性变换积分算法的互感器传变特性较好,鲁棒性较高;
(3)从不同输入信号突变的动态跟踪能力的比较分析可以看出,当输入信号幅值突变时,不同积分算法的互感器能较好地还原特性,相比Simpson算法存在较大的误差;当输入信号含直流分量时,采用双线性变换积分算法的互感器传变特性较好,尤其是在积分环节输入有直流分量情况。
从上述结论可以看出,采用不同积分算法时电子式电流互感器的频带特性和稳态传变特性较好,并没有显著的差别;但在动态特性方面,尤其在积分初值不确定、输入信号富含直流分量和高频谐波分量时,能较好地适应其抗干扰能力和动态跟踪能力方面的数字积分算法还有待进一步研究。
