基于仿真对比的电池等效电路模型分析*

徐佳宁，裴磊，徐冰亮，武国良，朱春波

（1.哈尔滨工业大学电气工程及自动化学院，哈尔滨150001；2.黑龙江省电力科学研究院，哈尔滨150031）

0 引 言

电池作为电动汽车的动力能源，从最初的铅酸电池到镍氢电池和超级电容，再到现在的锂电池，锂电池相比过往电池在重量和能量利用率等方面已经取得大幅度提高。电池由于长时间使用产生的老化和自放电等现象而表现出了高度的非线性。电池模型则是对电池动态特性的描述和简化［1］。国内外许多专家都致力研究准确描述电池特性的等效模型，现主要包括电化学模型［2］、电池热模型［3］、藕合模型［4］、性能模型四种类型［5］。每一种等效模型都有各自的优缺点，如何兼顾模型的复杂程度和精确程度成为当前研究的主要问题。

等效电路模型为性能模型中的一种［5］，是目前在电池模型中既考虑简化程度，同时也兼顾精确程度的等效模型，其使用电阻、电容和电压源等简单电子器件组成电路网络，计算量小，精度高。文章首先对纯电阻等效电路模型（Rint Model），戴维南等效电路模型（Thevenin Model），双极化等效电路模型（Dual Polarization Model，简称DP模型）和分数阶等效电路模型（Fractional Order Model）中的参数进行分析。通过Matlab，运用最小二乘法对四种等效电路模型在HPPC测试下进行参数辨识。将参数辨识后的结果代入电池端电压公式，对比四种等效电路模型端电压和实际实验数据的电池端电压误差和均方根误差（RMSE）。对比分析电池SOC在整个周期，以10%为间隔，每点SOC下带有RC并联网络结构等效电路模型的RMSE。以80%SOC点为例，证明DP等效电路模型的端电压可以很好的重合实验数据。最后对LiFePO4进行FUDS工况测试，分析DP等效电路模型不同温度下电池端电压的误差值，得到电池低温特性不好的结论。

1 锂离子电池等效电路模型

1.1 纯电阻等效电路模型

纯电阻（Rint Model）等效电路模型［6］较为简单，其结构如图1所示，其中包含开路电压Uoc和电池内阻Ro，IL为流过Ro的负载电流，Ut为模型端电压。端电压如公式（1）所示。

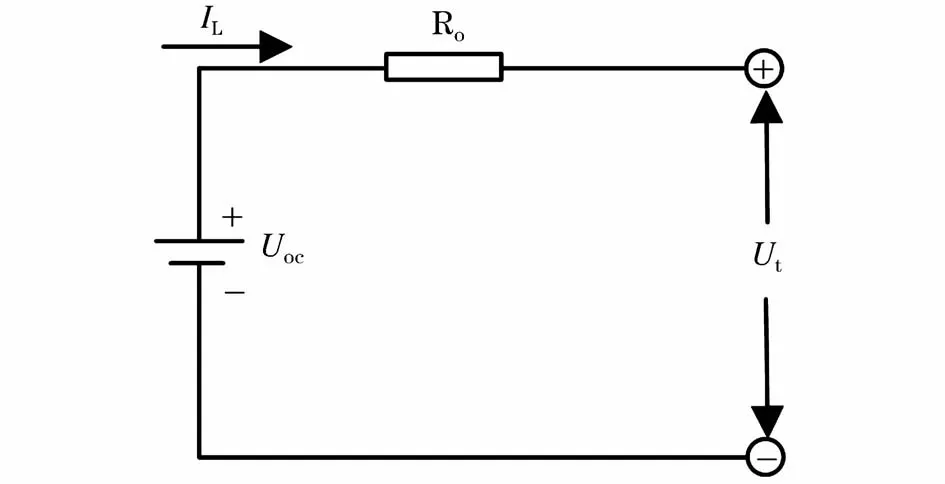
图1 纯电阻等效电路模型示意图Fig.1 Schematic diagram of Rint equivalent battery equivalent circuitmodel

这种模型的缺点为模型结构过于简单，由于电池内部的结构很复杂，温度或电解液浓度的变化都会引起电池内部Ro的变化，电池内部的特性很复杂，简单的Rint等效电路模型很难描述其内部特性。因此，电动汽车领域很少使用这种模型。

1.2 戴维南等效电路模型

Thevenin等效电路模型在Rint等效电路模型的基础上增加一个并联RC网络，RC网络的性质恰好与电池内部极化现象相符合，可以很好的体现电池内部动静态特性［7］。Thevenin等效电路模型结构如图2所示，主要由开路电压Uoc、欧姆内阻Ro和极化内阻Rp、极化电容Cp三个部分组成，其中Rp和Cp构成的并联环节用来描述电池的极化现象［8］。端电压如公式（2）所示。

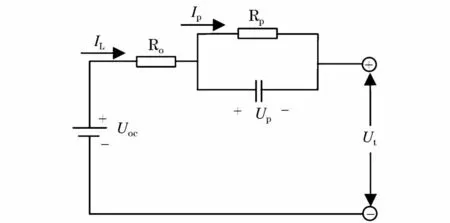
图2 戴维南等效电路模型示意图Fig.2 Schematic diagram of Thevenin equivalent battery circuitmodel

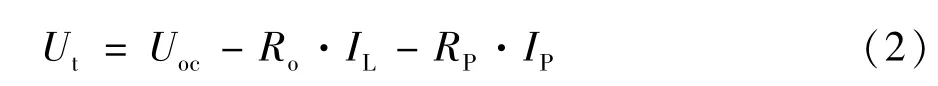
大量试验表明，当电池有电流流过时，电池的端电压既呈现了突变性，也表现出了渐变性，其中内阻Ro导致了电池端电压的突变性，极化电容Cp决定了电池端电压的渐变性。相比照于Rint等效电路模型，Thevenin等效电路模型考虑了温度等因素对模型精度的影响，而且电路结构也不复杂，因此电动汽车领域中应用比较广泛，但是模型在精度上还有待于提高。

1.3 双极化等效电路模型

分析锂离子动力电池的特点，可以发现一个明显的极化现象。通常在要求不高的情况下，电池的极化特性可以由Thevenin等效电路模型模拟。然而，电池内部的浓差极化和电化学极化对电池的充放电效率有很大影响［9］，使得Thevenin等效电路模型对电池的充电初期和充电后期的模拟均不准确。在此基础上重新改进得到的电路模型，被定义为DP等效电路模型。它对于电池内部的浓差极化和电化学极化，在Thevenin等效电路模型的基础上增加了一个RC网络，可以精确的描述出电池的全部极化特征，该模型结构较简单而且与电池外特性近似程度较高，模型原理如图3所示。

图中Rpa、Rpc之和视为电池的极化内阻，电池端电压的突变性由Rpa、Cpa构成的RC并联网络体现，电池端电压的渐变性由Rpc、Cpc构成的RC并联网络体现，前者时间常数较小，后者时间常数较大。

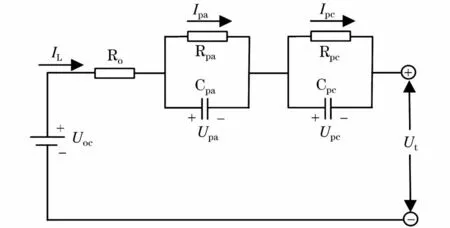
图3 双极化电路模型示意图Fig.3 Schematic diagram of DP equivalent battery circuitmodel

DP等效电路模型包括开路电压Uoc，欧姆内阻Ro，极化内阻 Rpa与 Rpc，极化电容 Cpa与 Cpc。其他物理量如图所示。由电路可以得到端电压公式如公式（3）所示。

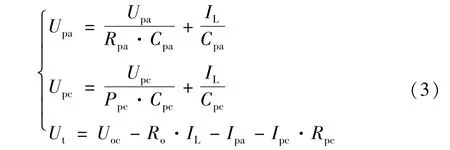
其中极化电流 Ipa由式（4）、式（5）得来：

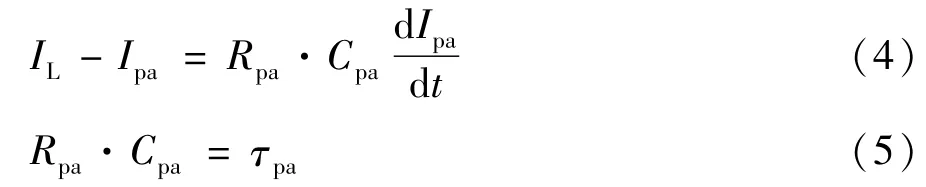
运用拉氏变换将时域函数变换到频域函数，有：

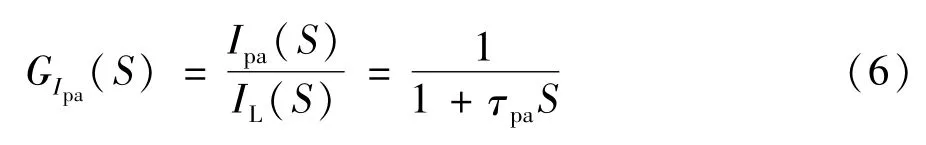
其中：

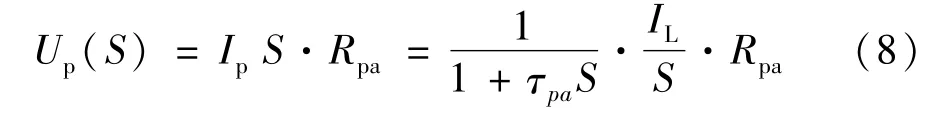
运用离散的方法，Rpa·Cpa电路在第k个采样点的零状态响应为：

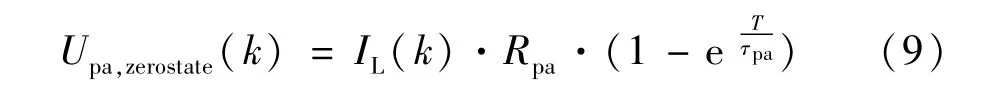
式中T为电流和电压采样周期。Rpa·Cpa电路的零输入响应为：

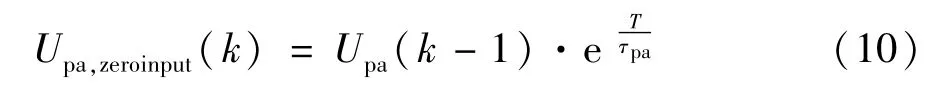
Rpa·Cpa电路在第k个采样点的电压值应为：

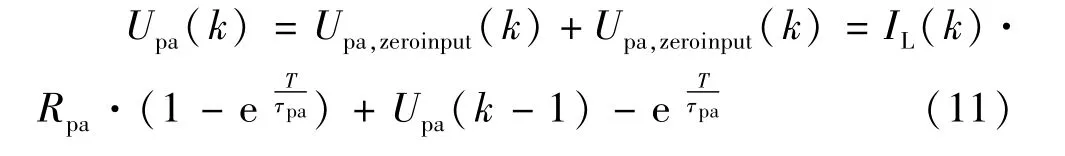
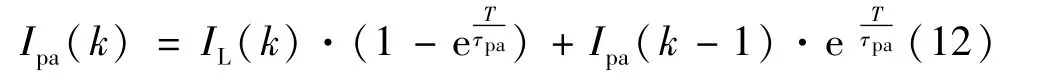
极化电流Ipc同理可得到为：

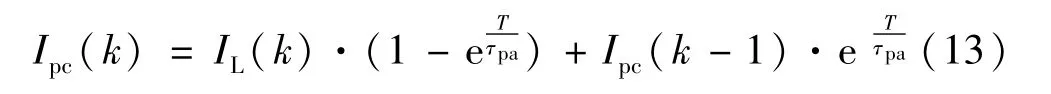
1.4 分数阶模型

国内外相关研究表明，电化学阻抗谱模型在估计电化学系统上有很高的精度，由于电化学阻抗谱模型的方法过于复杂，导致无法实时被应用。在借鉴电化学阻抗谱模型的优点的基础上，由于很多系统都具有分数特性，国外已经有研究表明可以采用分数阶模型来估计电池的SOC。但是由于计算的复杂性，并且在实验过程中其欧姆电阻并不能很好收敛，该方法用于电池SOC估计还有提高改进的空间，其模型原理图如图4所示，端电压如式（14）所示。

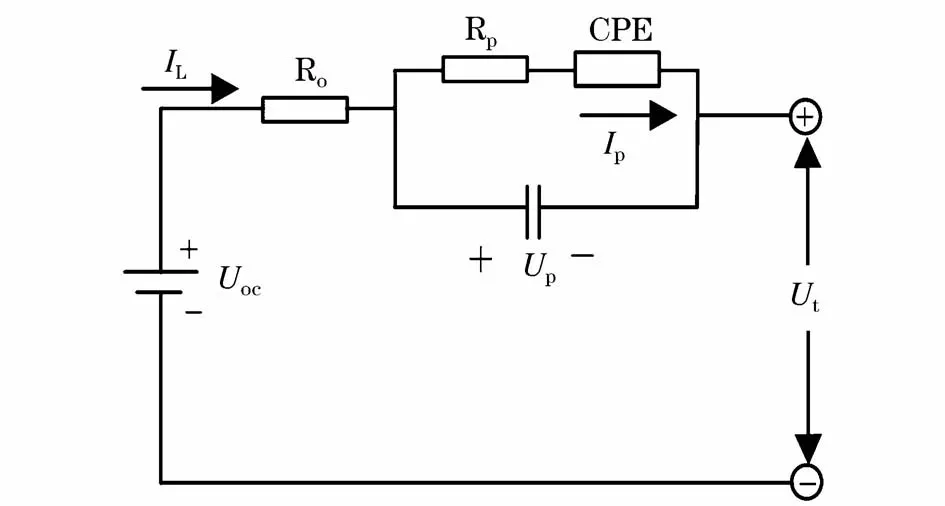
图4 分数阶电路模型示意图Fig.4 Schematic diagram of fractional order equivalent battery circuitmodel

2 实验内容

文章试验对象为容量为5 Ah的磷酸铁锂电池，其基本参数如表1所示。

表1 电池参数表Tab.1 Battery parameters

试验平台如图5所示，包括一台高低温实验箱（温度范围为-50℃～150℃）、Arbin-BTS2000专用电池检测设备（电流和电压输出精度和分辨率分别为±0.1%和±0.01%）和一台内置实验测试软件的电脑主机。

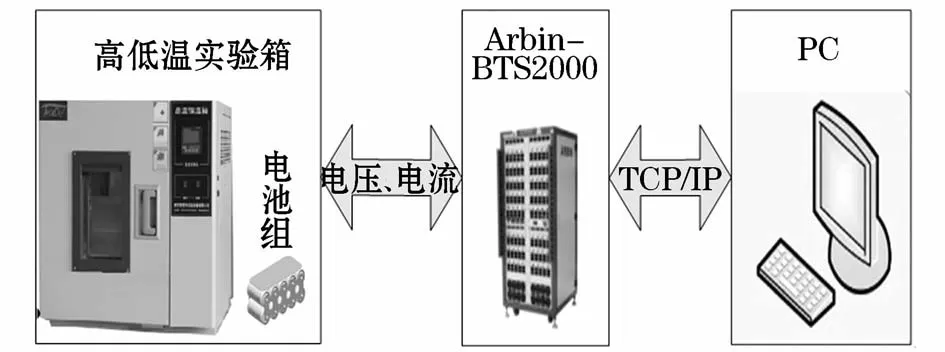
图5 电池测试台示意图Fig.5 Schematic diagram of battery test bench

HPPC测试，即在允许的充放电电压范围内，以确定电池动态特性为目的的脉冲充放电测试，用于等效电路模型参数辨识和精度对比分析。将电池放置于温箱中，直至电池到达平衡状态（通常6 h以上）。对电池以1/3 C进行恒流充电，到截止上限电压时停止充电，静置1 h。调节电池所需电池测试温度，将电池放入温箱中静置6 h。对电池以1/3 C的电流恒流放电，电池SOC减小10%后静置2 h。对电池以1/2 C的电流恒流放电10 s，然后静置40 s。以电池以1/2 C的电流恒流充电10 s，然后静置60 s。重复上述脉冲充放电步骤，当电池SOC=0.1时，停止充放脉冲充放电验。对电池以1/3 C恒流放电，当到截止电压时停止放电，将电池静置2 h后实验全部结束。实验过程中HPPC测试的电流和电压变化情况如图6所示，采样间隔是1 s。

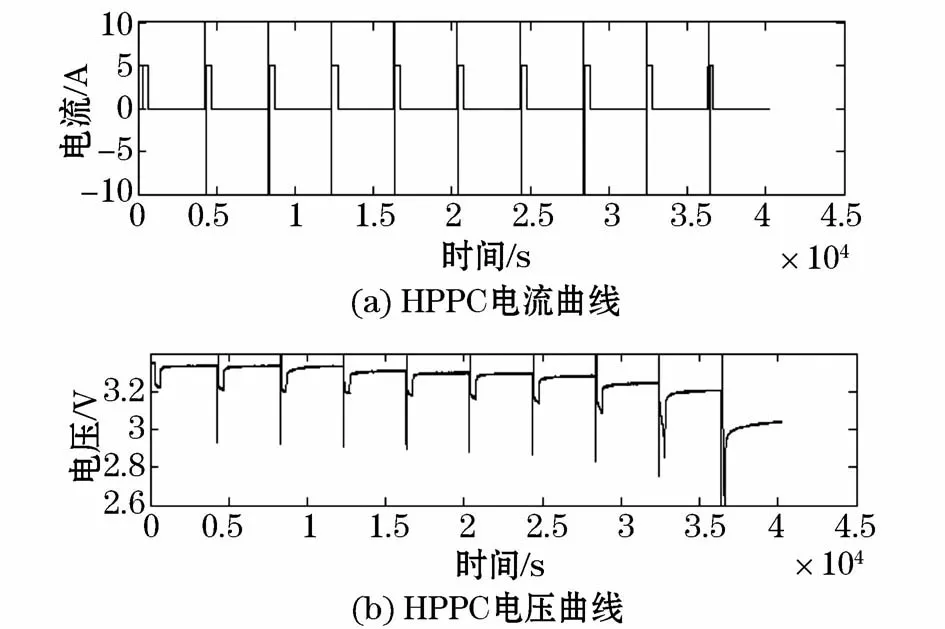
图6 HPPC电流及电压变化图Fig.6 Current and the voltage vs.time profile of HPPC

FUDS工况测试作为美国城市运行工况的检测标准，经常被用在仿真及实验验证中，来评估车辆的性能、控制策略的效果和SOC估算方法等，现在已经被全世界的许多实验室用于实验仿真分析。FUDS测试一般情况下是针对动态电流中的一段进行充放电，当电池电量减少到预定值时停止。电流段的选择可以按照测试规范的要求和系统限制按比例进行缩放。FUDS完的一个循环周期为1 372 s，它在循环过程中的电流及电压变化如图7所示。

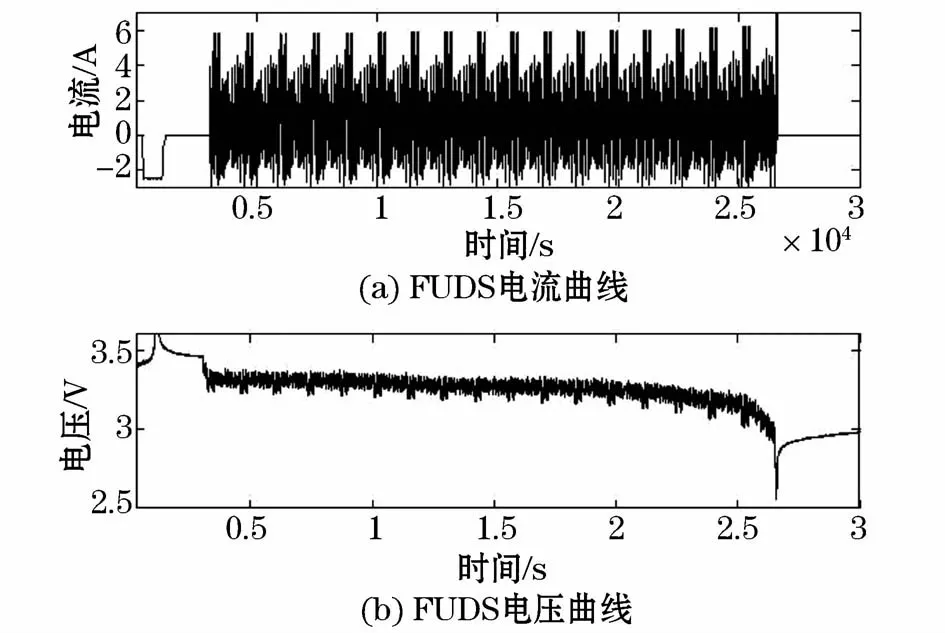
图7 FUDS电流及电压变化图Fig.7 Current and the voltage vs.time profile of FUDS

3 参数辨识

基于实验结果，对比模型精度需要对模型进行参数辨识。参数辨识即为实验结束后对实验数据进行处理的过程，文章采用最小二乘法（LS）对模型进行参数辨识。LS算法的原理为根据观测值对未知参数进行估计，当计算结果与实际观测值之差的平方和最小时，所求参数为最优估计。

4 试验结果分析

在HPPC测试下，分别对上述四种模型进行参数估计，将基于模型得到电池端电压与实验数据的误差和RMSE进行对比分析，如图8所示。

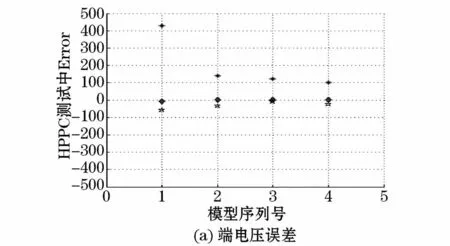
图8 HPPC测试下电池端电压误差RMSEFig.8 Error and RMSE in the HPPC test

图8表明，第一项Rint模型的最大电压误差明显高于其他三种模型，最小电压误差也大于其他三种模型；图中第三项为具有二阶RC网络的DP等效电路模型，其在误差和RMSE中均优于图中第二项只有一阶RC网络的Thevenin等效电路模型。由图8中还可以看出DP模型和图中第四项分数阶模型都具有良好的估计精度，并且都拥有相对较小的RMSE，但是分数阶模型只是初步的尝试阶段，很多技术并不成熟，目前其结果在SOC估计中效果并不理想。

将带有RC网络的三个等效电路模型在整个电池SOC周期范围内进行对比分析，如图9所示。图中可以看出带有0阶RC的Rint等效电路模型在整个周期内的RMSE均远大于带有一阶RC网络的Thevenin等效电路模型和带有二阶RC网络的DP等效电路模型。DP等效电路模型在整个周期内的RMSE值均为最小，说明DP等效电路模型的精度最高。从图中还可以看出，在电池SOC为0%～10%范围内，三个等效电路模型的RMSE均比其他任何阶段的值高出很多。这说明，当电池进行深度放电时等效电路模型的精度会骤降。因此，在电池进行充放电过程中应避免对电池进行深度放电。另外，如何对模型进行改进来增加SOC在较低范围内的估算精度，也是未来电池等效电路模型研究的重点。

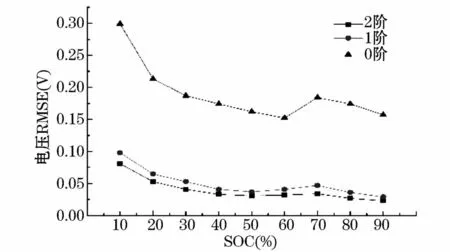
图9 SOC所有范围内的电压RMSE对比Fig.9 Voltage RMSE comparison in the entire SOC range

文章以80%SOC处为例，图10为DP等效电路模型的端电压与实验数据的曲线，其中蓝色为基于模型的估计值，红色为实验数据真实值。从图中可以看到DP等效模型可以很好的模拟真实曲线，具有很好的精度。

如图11所示，文章在FUDS测试下基于DP等效电路模型分别在10℃、30℃和50℃对模型的端电压误差进行对比。

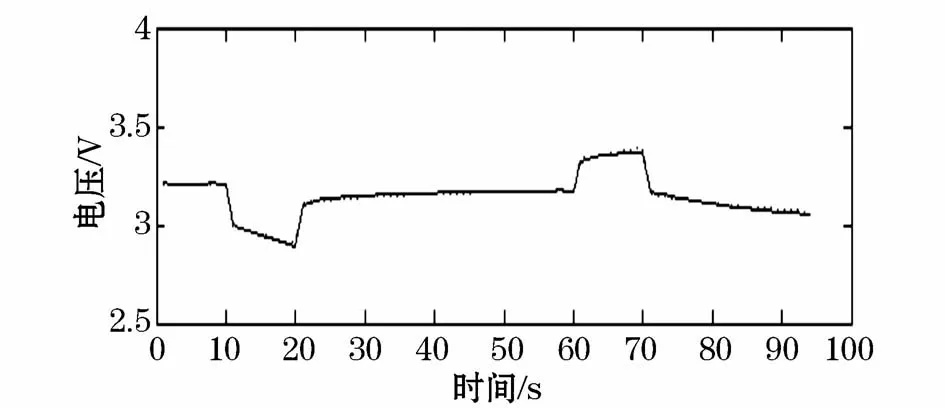
图10 DP模型端电压估计曲线Fig.10 Estimation curve of terminal voltage cycles of DPmodel

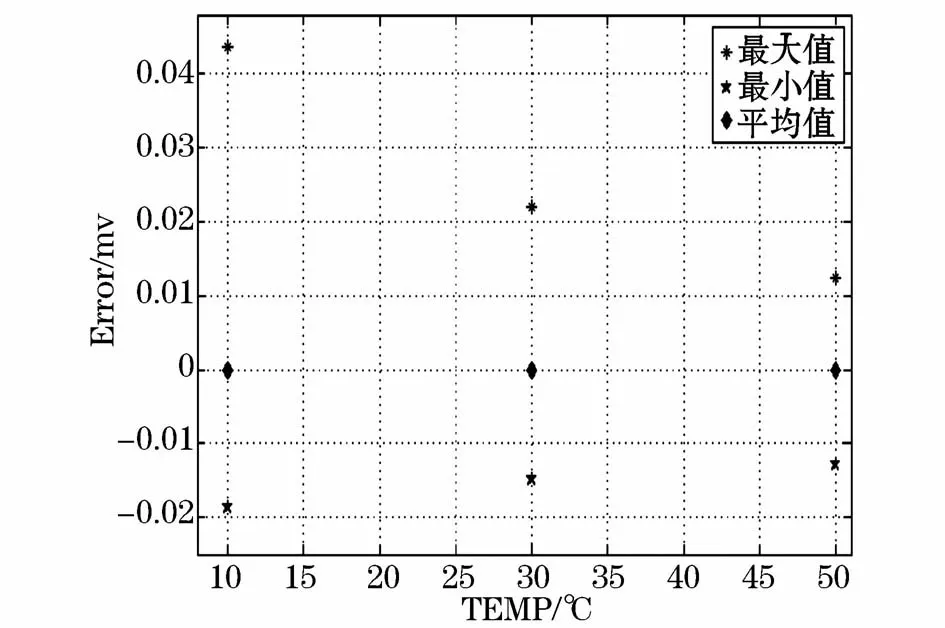
图11 FUDS测试下不同温度端电压误差Fig.11 Error under different temperatures in FUDS test

从图中可以看出温度对电池模型的精度有影响，同时也说明电池的低温特性不是很好，必须在合适的温度下才能有较好的精度。当电池温度较高时，电池活性增加，能量能够得到有效的输出，表现为充放电效率提高，但电池长时间处于高温环境下，安全性和使用寿命都会降低；当电池处于低温情况下，其充放电效率又会明显降低，而且在低温环境下，Li+的脱嵌能力也会下降，为了防止Li+的沉积造成安全隐患，在低温环境下必须减小电池的充放电电流。所以在充放电试验中，需要将电池放置在合适的温度下才能保证电池SOC的准确测量。

4 结束语

如何确定电动汽车的SOC和继续行驶能力，需要合适的等效模型对其进行准确估计。文章针对通过物理模型准确模拟电池特性的问题，对 Rint，Thevenin，DP和Fractional Order四种等效电路模型进行研究。通过HPPC测试对四种等效电路模型进行对比分析，得到了DP等效电路模型在电池端电压误差和RMSE两个方面均优于其他三种模型的结论。在FUDS工况测试下通过仿真分析，在整个电池SOC范围内带有二阶RC网络的DP等效模型相比带有0阶RC和一阶RC的等效电路模型具有精度高，动态性能好等优点。同时，大量资料显示，并不是带有越多的RC网络，精度就会越高，当RC网络的阶数达到三阶以及三阶以上时，模型的精度不会再有明显提高，同时伴随有非常大的计算量［10］。通过对不同温度下的DP等效电路模型的误差进行分析，得到了温度电池模型的精度有一定程度上影响，电池低温特性不好的结论。综合以上所有结果显示，DP等效电路模型无论从模型精度还是计算量的选择上均具有很好的表现，为电池SOC的准确估计奠定了基础。