不对称电网电压下MMC-HVDC系统功率波动抑制策略研究*

2017-12-20刘英培潘朏朏栗然张栋

电测与仪表 2017年2期

刘英培，潘朏朏，栗然，张栋

（1.华北电力大学电气与电子工程学院，河北保定071003；2.国网河南省电力公司濮阳供电公司，河南濮阳457000）

0 引言

近年来，基于电压源换流器的柔性直流输电（Voltage Source Converter based High Voltage Direct Current，VSC-HVDC）系统较传统的基于晶闸管的高压直流输电系统有着可向无源网络供电、实现有功和无功解藕控制等优点，在可再生能源并网、交流异步联网等场合得到了越来越多的应用［1］。模块化多电平换流器（Modular Multilevel Converter，MMC）作为柔性直流输电技术的一种新型拓扑结构，可通过多个子模块输出电压的叠加得到较高的直流电压等级，避免了开关器件的直接串联；同时大大降低了换流器阀侧输出交流电压的谐波含量；此外MMC开关损耗较低，易于模块化制造，故障穿越能力强，更适用于柔性直流输电领域。因此众多学者对其数学模型、控制及保护策略进行了大量研究［2-5］。

在电网电压不对称时，由于系统三相电压、电流中存在负序分量，这将导致MMC交流侧输出的有功功率和无功功率产生二倍频波动。为提高电网电压不对称情况下MMC-HVDC系统的动态和稳态运行性能，需对MMC交流侧功率波动进行抑制。

关于功率波动的抑制，最初的控制策略是对电网电压、电流进行正负序分解后，将电网正序、负序电压分别定向至正序、负序dq坐标系下，从而分别形成正、负序网络，进行电流矢量控制，该控制策略在电流控制环节需用到4个比例积分（Proportional Integrator，PI）调节器，而且由于控制自由度的限制，只能抑制有功及无功功率波动其中一种［6-7］。同时，电量的正负序分解会增加控制复杂度，并使控制系统存在一定的延时。文献［8-9］在αβ坐标系下引入了滞后于原电网电压α、β轴分量90°电角度的电压分量，无需进行电量的正负序分解便可分别实现抑制有功功率或无功功率波动的控制目标，然而该控制策略并不能同时抑制有功及无功功率的波动。文献［10-11］提出了换流器的谐振直接功率控制策略，该控制策略使用2个PI调节器及2个比例谐振调节器或矢量比例积分调节器可以达到同时抑制有功及无功波动的控制目标。

为了同时抑制电网电压不对称条件下MMC交流侧输出有功功率与无功功率波动，本文将交流电压、电流均变换至正序dq坐标系下，并将电网正序电压定向至正序d轴上，提出了一种新的电流计算方法，进而进行电流矢量控制。该控制策略在电流控制环节使用2个比例积分谐振（Proportional Integrator Resonant，PIR）控制器即可达到控制目标，且无需进行电流的正负序分解。此外，为实现电压、电流的正序dq变换，本文设计了基于二倍频陷波器的频率自适应锁相环，在电网电压不对称条件下可以准确锁定正序电压相位，同时计算正序电压幅值及负序电压在正序d、q轴上的分量值，用于电流参考值的计算。

1 MMC拓扑电路及其数学模型

1.1 MMC拓扑电路

MMC拓扑结构如图1所示。图1中，uk（k=a，b，c）为 k相等效电动势，RAC、LAC分别为交流侧等效电阻、电抗，R0、L0分别为每个桥臂等效电阻、电抗，Udc、Idc分别为直流侧电压、电流。该拓扑三相结构对称，共三相六桥臂，每桥臂级联N个子模块（SM）。

图1 MMC拓扑结构Fig.1 Topological structure of MMC

MMC子模块内部结构亦在图1虚线框中给出。每个子模块由两个带有反并联二极管的IGBT串联后，再与一个电容并联组成。子模块电压、电流正方向已在图1中标出，iSM、uSM分别为流入子模块的电流及子模块输出电压。子模块共有以下4个工作状态：

（1）iSM＞0时，若 T1导通，T2截止，此时电流经D1向电容充电，子模块输出电压为电容电压UC，子模块处于投入状态；

（2）iSM＞0时，若 T1截止，T2导通，此时电流经T2流出，将电容旁路，子模块输出电压为0，处于切除状态；

（3）iSM＜0时，若 T1导通，T2截止，此时电容经由T1放电，子模块输出电压为电容电压UC，处于投入状态；

（4）iSM＜0时，若 T1截止，T2导通，此时电流经由D2流出，将电容旁路，子模块输出电压为0，处于切除状态。

因此，MMC工作时保证任何时刻每相投入的子模块数恒定为N，即可维持直流电压恒定，此时Udc=NUC。

1.2 MMC数学模型

MMC单相等效电路如图2所示。图2中，ik为k相交流电流，Uk1、Uk2分别为k相上、下桥臂子模块电压总和，ik1、ik2分别为 k相上、下桥臂电流。upk、unk分别为k相上、下桥臂电抗器末端电压。

图2 MMC单相等效电路Fig.2 Single phase equivalent circuit of MMC

经推导可得upk=unk［12］，因此每相上、下桥臂电阻、电抗可以并联成一个电阻、电抗，与交流系统相连，简化后的等效电路如图3所示，图3中，L=LAC+L0/2，R=RAC+R0/2。

图3 MMC单相简化等效电路Fig.3 Simplified single phase equivalent circuit of MMC

图2中，令：

设上、下桥臂子模块电压总和参考值分别为Uk1_ref、Uk2_ref，直流电压参考值为 Udcref，则以下关系式成立［13］。

由图3可得MMC交流侧数学模型为：

2 电压不对称时MMC功率波动抑制

2.1 电压不对称时MMC特性分析

由于MMC交流侧变压器通常为Y/Δ接法，零序电流无流通回路。故当电网电压不对称时，只考虑三相电压、电流的正序和负序分量。将MMC交流侧数学模型式（4）变换至正序dq坐标下，可以得到：

式（6）、式（7）中，ud+、uq+、id+、iq+分别为交流电压、电流的正序分量在正序d、q轴上的投影，该值为直流量；分别为交流电压、电流的负序分量在正序d、q轴上的投影，该值为二倍频分量。

2.2 功率波动抑制方法

在正序dq坐标系下，MMC交流侧输出的有功功率P和无功功率Q可分别表示为［11］：

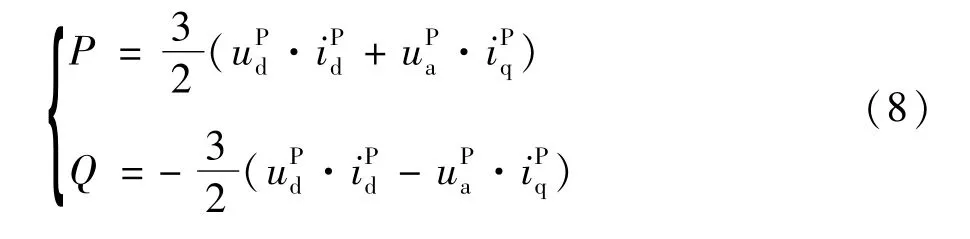
将式（6）、式（7）代入式（8），则电网电压不对称条件下MMC交流侧的有功功率和无功功率可分别表示为：

设Pref、Qref分别为有功功率及无功功率参考值，为同时抑制有功功率和无功功率的波动，式（9）中，令：

如此便可同时消除有功功率和无功功率的二倍频波动，且使功率的直流量分别跟踪有功功率及无功功率的参考值［15］。

将电网正序电压定向至正序d轴上，则可得ud+=UmP，uq+=0，其中，UmP为电网电压正序分量幅值。将式（10）代入式（9）中，求解可得电流参考值为：

式中id+ref、iq+ref分别为正序电流在正序d、q轴上的参考值；分别为负序电流在正序d、q轴上的参考值。

则正序 d、q轴上总的电流参考值 idref、iqref分别为：

功率波动抑制策略控制原理如图4所示。

图4 功率波动抑制控制原理图Fig.4 Principle diagram of power fluctuation suppression control

参考电流计算环节根据式（11）～式（13）计算出正序d、q轴总的电流参考值后，根据式（5）设计电流控制环节，最后得到d、q轴上桥臂电抗器末端输出电压参考值再进行 dq反变换，得到MMC k相桥臂电抗器末端输出电压参考值urk_ref。由于在正序dq坐标系下，负序电压、电流均表现为二倍频形式，而传统PI控制器只能实现对直流量的无误差跟踪，因此本文电流控制环节采用PIR调节器，其传递函数如式（14）、式（15）所示。

式（14）中，KP1、KP2、Ki1、Ki2、KR1、KR2分别为 PIR调节器的比例、积分、谐振系数；ωc为截止频率，一般取5 rad/s～15 rad/s，此处取 ωc=10 rad/s；ω0为谐振频率，取 ω0=2ω。

3 锁相环设计

电网电压不对称时，在正序dq坐标下，交流电压的负序分量在d、q轴上表现为二倍频波动形式。式（6）已给出电压在正序d、q轴上的表达式，且：

式中UmN为电压负序分量幅值，φ为负序电压初相角［16］。

交流电压进行正序dq变换后，本文采用陷波器滤除其中的二倍频分量，陷波器传递函数为［17］：

式中ωn为陷波角频率；ξ为阻尼系数。此处取ξ=0.707，ωn=2ω。

为了使该陷波器能够根据电网频率变化准确滤除给定频率的正弦信号，本文在陷波器中加入频率自适应环节，使得陷波器能够根据电网频率的变化准确地滤除二倍于电网频率的交流信号。所设计的锁相环原理如图5所示。交流电压uabc经正序dq变换后，d、q轴分量中含有正序电压形成的直流量和负序电压形成的二倍频分量；经d、q轴陷波器后分别输出直流量与相减后，可得二倍频分量再经后续PI控制及积分运算即可得出正序电压相角。

图5 锁相环设计原理图Fig.5 Design diagram of PLL

至此，结合本文所提的功率波动抑制方法及锁相环设计方法，MMC-HVDC系统总体控制原理如图6所示。交流侧电压经本文所设计的锁相环后输出正序电压相角ωt，用于dq变换。且本文所设计的锁相环节可同时计算出交流电压中正序、负序分量在正序 d、q轴上的投影用于电流控制环节中参考电流的计算。参考电流经图4所示的电流控制环节，输出MMC k相桥臂电抗器末端电压参考值 urk_ref。根据式（2）、式（3），urk_ref与 Udcref/2相互作用后，作为换流器k相上、下桥臂子模块电压总和参考值 Uk1_ref、Uk2_ref。最后进行载波移相调制［18］，控制MMC运行。

图6 系统整体控制原理图Fig.6 Overall control block diagram of the system

4 仿真研究

两端MMC-HVDC系统如图7所示，为验证本文所提控制策略的可行性和有效性，在Matlab/Simulink环境下搭建系统仿真模型，系统参数如表1所示。系统整流侧采用定有功功率和定无功功率控制策略，逆变侧采用定直流电压和定无功功率控制策略。

图7 MMC-HVDC系统Fig.7 Model of MMC-HVDC system

表1 仿真系统参数Tab.1 Parameters of the simulation system

4.1 锁相环功能仿真验证

图8 网侧电压Fig.8 Grid voltage

在0.3 s～0.4 s时，电网A相电压跌落10%，图8为电网电压波形，图9为锁相环输出相位。由于所设计的锁相环锁定正序电压相位，因此锁相环初始相位并不为0。由图9可以看出，电网电压不对称情况下，所设计的锁相环能够准确锁定正序电压相位，为MMC-HVDC系统控制策略提供了准确的相位。

图9 锁相环输出相位Fig.9 Output phase of PLL

为验证锁相环的频率自适应特性，在0.3 s～0.4 s时，电网频率下降5 Hz。图10为电网电压波形，图11为锁相环输出角频率ω。由图11可以看出，当交流电压频率下降时，该锁相环能够稳定跟踪电网电压角频率变化，进行准确输出。

图10 网侧电压Fig.10 Grid voltage

图11 锁相环输出角频率Fig.11 Output angular frequency of PLL

4.2 对功率波动抑制的仿真验证

整个控制过程中，整流侧有功功率和无功功率给定值不变，分别为0.5 MW和 -0.25 MVar。在0.3 s～0.4 s时，整流侧A相电压跌落10%，分别采用传统控制方法［19］与本文所提控制方法时，整流侧有功功率和无功功率波形分别如图12、图13所示。

图12及图13中，P1、Q1分别为采用本文控制方法时整流侧有功功率及无功功率波形，P2、Q2分别为采用传统控制方法时整流侧有功功率及无功功率波形。由图12及图13可以看出，当整流侧交流电压发生单相跌落时，若采用传统控制方法，有功功率及无

图12 有功功率波形对比Fig.12 Comparison of active power waveform

图13 无功功率波形对比Fig.13 Comparison of reactive power waveform

功功率产生了较大的二倍频波动；且在系统启动后，有功功率和无功功率经0.2 s后才能达到稳定状态。而采用本文所提方法后，电网电压不对称条件下，MMC交流侧有功功率及无功功率的二倍频波动均在较大程度上得到了抑制；同时，系统启动后0.05 s内功率便可稳定跟踪其给定值。

本文所提控制策略下正序d、q轴电流跟踪仿真波形分别如图14、图15所示。从图14、图15中可以看出，电网电压对称时，电流实际值能很好地跟踪电流参考值。而电网电压不对称时，由于负序电流的作用使得电流参考值idref、iqref中除直流量外，还含有二倍频分量，采用本文所提方法可使实际电流id、iq在电网电压不对称情况下稳定地跟踪其参考值。