三种相依随机序列的M估计的渐近正态性

余新新，胡宏昌，刘 香

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

三种相依随机序列的M估计的渐近正态性

余新新，胡宏昌，刘 香

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

随机变量的渐近正态性是统计学中研究的热点之一.利用负相协(NA)、负超可加相依(NSD)、渐近几乎负相依(AANA)三种相依随机序列的性质及一些不等式，在适当的条件下得到了三种相依随机序列的M估计的渐近正态性.这些结果推广了独立随机变量序列的相应结论.

相依随机序列；M估计；渐近正态性

0 引言

关于独立同分布随机变量的渐近性质的研究已经有许多经典的结果,如林正炎、陆传荣和苏中根[1]系统讲述了独立随机变量序列的中心极限定理.然而在实际生活中，多数变量是相依的，所以很多人关注相依随机变量的渐近性质.负相协(NA)、负超可加相依(NSD)、渐近几乎负相依(AANA)随机序列就是常见的相依变量.

Joag-Dey K和Proschan F[2]提出了NA的概念，而NSD是较NA更为广泛的一种随机变量，Hu[3]提出了NSD的概念，并给出了NSD的一些基本性质.文献[4]指出了NA序列是AANA序列.文献[5]讨论了非平稳同分布NA序列的中心极限定理的一些结果.文献[6]研究了相协随机变量函数的部分和的中心极限定理.文献[7]给出了NA部分和之随机变量和的中心极限定理.本文在前人的基础上研究了三种相依序列的渐近正态性.下面给出三种相依随机序列及M估计的概念.

定义1[2]称实值随机变量X1,…,Xn(n≥2)是NA的，如果对于{1,…,n}的任意两个不相交的非空子集A1与A2,都有

cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0

其中f1与f2是任何两个使得协方差存在的且对每个变元均非降(或对每个变元均非升)的函数.称随机变量序列{Xj,j∈}是NA序列,如果对每个n≥2，变量X1,…,Xn都是NA的.

定义2[3]称{X1,X2…,Xn}是NSD的，如果满足

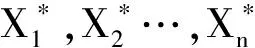
定义3[8]称{Xn,n≥1}是AANA的，如果存在非负q(n)→0(n→∞)，对任意的n,k≥1都有

其中f和g是任何两个使上述方差存在且对每个变元均为非降的连续函数.称{q(n)≥1}为该AANA序列的混合系数.

1 主要结果

假设{X1,…,Xn}为NA(或NSD或AANA)随机变量序列，为了本节定理的证明，下面给出定理所需要的一些基本条件：

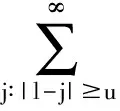
3)Xj,j≥1在L2上一致可积；

5) 存在严格上升的自然数序列{nk},对某个α∈(0,1)满足

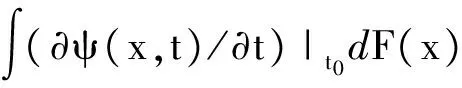
定理1 {X1,…,Xn}是NA或AANA随机变量序列，分布函数为F(x)，且满足条件(1)～(2)和条件(4)～(7)，则

定理2 {X1,…,Xn}是NSD随机变量序列，分布函数为F(x)，且满足条件(1)～(7)，则

定理3 {X1,…,Xn}是NA或AANA随机变量序列，分布函数为F(x)，且满足条件(1)～(2)、(4)～(5)和条件(8)～(9)，则

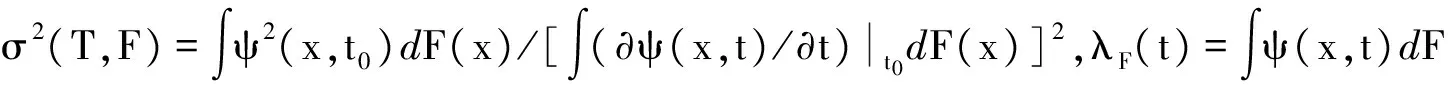
定理4 {X1,…,Xn}是NSD随机变量序列，分布函数为F(x)，且满足条件(1)～(5)和条件(8)～(9)，则

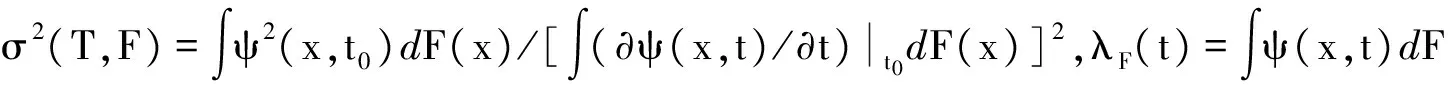
2 主要结果的证明

为了证明本节的结果，需要用到如下引理：

引理1[10]设{X1,X2…,Xn;n≥1}为NA(或NSD或AANA)随机变量序列，f1,f2,…是非降(或者非增)的连续函数，则{fn(Xn),n≥1}仍是NA随机序列.

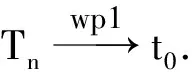
定理1的证明 假设ψ(x,t)关于t是非增的，则λFn(t)也是非增的.因此由引理2得

为了得到渐近正态性，需要证明

其中tz,n=t0+zσn-1/2,σ=σ(T,F),(6)式等价于证明

因此

-n1/2λF(tz,n)/Sz,n→z,n→∞

即

其中Φ为标准正态分布函数.

也就是要证明

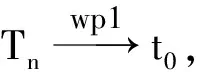
因为{Xi}是NA随机变量序列，所以由引理1可知{Yni}也是NA随机变量序列.利用文献[5]中定理的证明方法可以证明(8)式，在此略.定理2的证明过程和定理1类似，这里也不再证明.

定理2的证明 因为ψ(x,t)关于t是可微的，由中值定理得

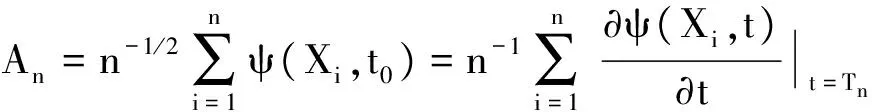
要证(3)式，只需要证明

由引理3得

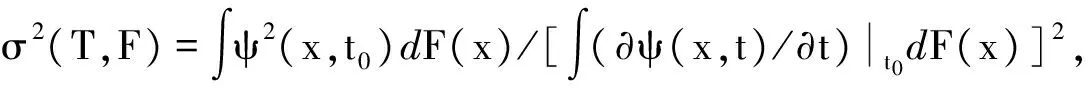
要证式(3)，只需证明

即证,

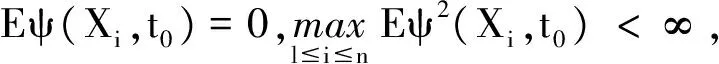
[1]林正炎,陆传荣,苏中根.概率极限理论基础[M]. 北京：高等教育出版社，1999.

[2]Joag-Dev K, Proschan F. Negative association of random variables with applications[J]. The Annals of Statistics, 1983,11(1):286～295.

[3]Hu T Z. Negatively superadditive dependence of random variables with applications[J]. Chinese Journal of applied probability and Statistic, 2000,16:133～144.

[4]Chandra T K, Ghasal S. The strong law of number for weighted averages under dependence assumptions[J]. Journal of Theoretical Probability, 1996,19(3):797～809.

[5]苏 淳，迟 翔.非平稳NA序列中心极限定理的一些结果[J].应用数学学报，1998,21(1)：9～21.

[6]Zhao Y L, Qin Y S, Shen X X. Central limit theorem for sums of the functions with associated random variables[J]. Journal of zhejiang Normal University,2015,38(3):1～8.

[7]Zou G Y. Central Limit Theorem for Random Sum of Partial Sums of NA Sequences[J]. Journal of shenyang University of Chemical Technology, 2016,30(1):1～4.

[8]Chandra T K, Ghasal S. Extensions of the strong law of number of Marcinkiewicz and Zygmund for dependent variables[J]. Acta Mathematical Hungarica, 1996,71(4):327～336.

[9]Robert J Serfling. Approximation Theorems of Mathematical Statistics[M]. New fork:John Wiley & Sons, 1980.

[10]Yuan D M, An J. Rosenthal type inequalities for asymptotically almost negatively associated random variables and applications[J].Science in China Series A, 2009,52(9):1887～1904.

AsymptoticnormalityofM-estimatesforthreekindsofdependentrandomsequences

YU Xin-xin，HU Hong-chang，LIU Xiang

( College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China)

Asymtotic normality of random variables is a hot problem in Statistic. In this paper, using the properties of three dependent random sequences for negatively associated (NA), negatively superadditive dependent(NSD) and asymptotically almost negatively associated (AANA), and some inequalities, we obtain asymptotic normality of M-estimates for the three dependent random sequences under appropriate conditions. Theses results extend the corresponding conclusion of independent random variables sequences.

dependent random sequences;M-estimates;asymptotic normality

O211.4

A

2096-3149(2017)04- 0062-05

10.3969/j.issn.2096-3149.2017.04.013

2017—07—28

国家自然科学基金(11471105)，湖北师范大学科研团队(T201505)，湖北省教育厅科学技术研究项目(Q20172505，D20172501)

余新新(1994— )，女，河南驻马店人，硕士研究生,主要研究方向为统计学.