关于质点运动的矢量及其分量描述的一般讨论

李江林，黄小敏，蓝森军，陈 杨

(湖北师范大学 物理与电子科学学院，湖北 黄石 435002)

关于质点运动的矢量及其分量描述的一般讨论

李江林，黄小敏，蓝森军，陈 杨

(湖北师范大学 物理与电子科学学院，湖北 黄石 435002)

推导了质点的位置公式与速度公式的矢量表达形式及其在一个具体的坐标系中相应的分量形式。

质点；矢量形式；分量形式

0 引言

以牛顿定律为核心的理论体系，通常称为矢量力学(有时也叫“牛顿力学”)，因为这种体系是以位置矢量、位移、速度、加速度、力、动量等这些矢量为基本量来说明力学系统运动的。矢量表示的优点是当给定了参考系时，与选择具体的坐标形式无关，这便于我们作一般性的定义陈述和关系式的推导。当然在做具体计算时，我们必须根据问题的特点选择适当的坐标系。一个矢量的分解方式，在纯数学意义上其结果有各种可能性，在物理上究竟采用哪种分解方式，就是看其是否具有明确的物理意义，或者是否带来简捷的计算方法。下面的讨论能够进一步深化对这些问题的认识，使我们深刻地理解质点运动的矢量表达及其在一个具体的坐标系中相应的分量形式。

1 位置公式与速度公式[1,2]

取一参考系并在其中确定一个参考点O，以考察质点的运动。在图1所示的弓形矢量图中，每个小箭头表示一次微分位移dr=υdt，而宏观位移正是微分位移的矢量合成。

从矢量三角形OAB看，有：Δr=r(t)-r0，于是，任意时刻质点的位置矢量表示为：

其中r0为质点的初始位置矢量。

在速度空间中作类似的考察，如图2所示，弓形矢量图中的每个小箭头表示一次微分速度的改变量dυ=adt，宏观上的速度变化量Δr正是微分速度改变量的矢量合成。

于是，任意时刻质点运动的速度表示为：

其中υ0为质点运动的初始速度。

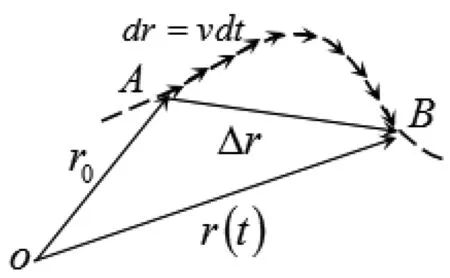
图1 导出位置公式的矢量图示

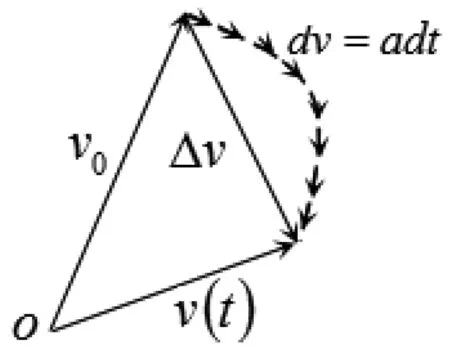
图2 导出速度公式的矢量图示

2 一类重要的匀加速运动

在地面上的低空区域运动的物体，在忽略空气阻力的情况下，其加速度a=g，为常矢量。例如，抛体运动、自由落体运动。

2.1 矢量形式

根据(2)式得到这类运动的速度表达式为：

根据(1)、(3)式进而得到这类运动的位置矢量表达式为：

特别是，如果初始位置矢量为r0=0，则：

2.2 分量形式

上面我们用矢量形式写出了质点运动的速度和位置矢量表达式，这种形式的优点是与具体的坐标系无关，只与参考系有关，因此以上结果对任何坐标系都适用。但是在具体计算时，矢量形式往往并不方便，通常将它们沿适当的坐标系的坐标轴进行分解，即将它们写成在该坐标系中的分量形式。

下面我们以一个典型例子来说明。有一抛体运动，如图3所示，∠xoy,∠x＇oy＇为直角，ox为水平方向，ox＇为抛体初速度υ0的方向，ox＇与ox的夹角为α，我们来分析它的几种分量形式[3,4]。

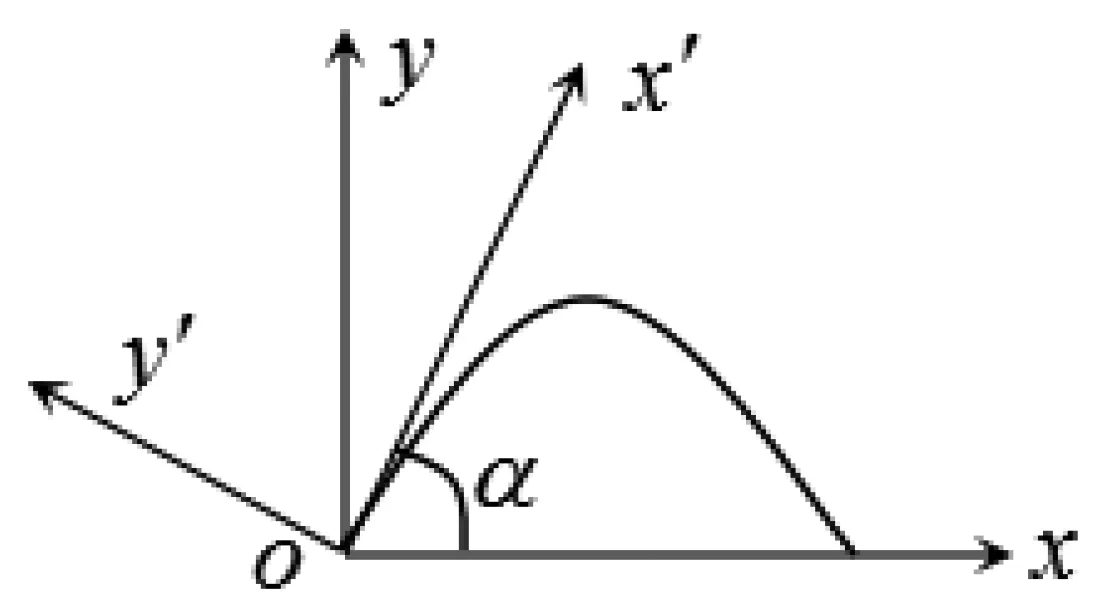
图3 斜抛运动图示

图4 沿x轴、y＇轴的分量图示

“一些常见的曲线运动往往可以分解为两个方向上的直线运动，分别研究这两个方向上的受力情况和运动情况，弄清楚作为分运动的直线运动的规律，就可以知道作为合运动的曲线运动的规律，这是研究曲线运动的基本方法。”[5]

1)我们将运动沿水平方向轴、竖直方向轴分解。水平方向无加速度，竖直方向加速度为-g，所以根据(4)式其分量形式为：

2)我们将运动沿x＇轴、y轴方向分解。即物体的运动可看成沿初速方向的匀速直线运动和自由落体运动的合运动，所以根据(4)式其分量形式为：

3)我们将运动沿x＇轴、y＇轴方向进行分解。x＇轴向初速为υ0，加速度为-gsinα；y＇轴向初速为零，加速度为-gcosα。所以根据(4)式其分量形式为：

4)我们将运动沿x轴、y＇轴方向进行分解。根据图4，可以得到：

所以根据(4)式其分量形式为：

3 结论

上面我们讨论和分析了质点作一般运动其位置公式与速度公式的矢量表达形式，还就其在地面上的低空区域运动，在忽略空气阻力的情况下，推导出了质点运动的矢量表达式及其在一个具体坐标系中相应的分量形式。矢量表示的优点是便于我们作一般性的定义陈述和关系式的推导，有时候在求解一些物理问题时用矢量解法进行分析和计算，比用分量形式计算更简捷、更凸显物理意义，例如空中打靶问题。上面的几种分量表达式，是对教材的拓展和深化，大大开阔了我们的眼界，当我们把一个复杂的运动分解为简单的运动进行研究时，我们有更多的选择，往往我们可以选用其中某一种分量形式进行计算和分析最为方便、简单。

[1]钟锡华,周岳明.大学物理通用教程:力学[M].北京:北京大学出版社,2000.

[2]郑永令,贾起民,方小敏.力学(第二版)[M].北京: 高等教育出版社,2002.

[3]祝之光.物理学(第三版)[M].北京:高等教育出版社,2009.

[4]祝之光.物理学(第三版)习题分析与解答[M].北京:高等教育出版社,2008.

[5]王运淼.对“运动的合成与分解”的理解与教学建议[J]. 物理通报,2012,(11):45～47.

Descriptionofparticlemotionvectoranditscomponentofgeneraldiscussion

LI Jiang-lin,HUANG Xiao-min,LAN Sen-jun,CHEN Yang

(College of Physics and Electronics, Hubei Normal University, Huangshi 435002,China)

In this paper,we discuss the vector expression form of the position formula and velocity formula of the particle and the corresponding component form in a specific coordinate system.

particle; vector form; component form

Q213

A

2096-3149(2017)04- 0093-03

10.3969/j.issn.2096-3149.2017.04.019

2017—08—23

李江林(1965— )，男，湖北安陆人，教授，硕士生导师.