用导数分析函数单调性的一个注记

陈引兰

(湖北师范大学 数学院统计学院，湖北 黄石 435002)

用导数分析函数单调性的一个注记

陈引兰

(湖北师范大学 数学院统计学院，湖北 黄石 435002)

由一道关于函数单调性高考题的常见解答错误，分析出错的根源，给出用导数分析函数单调性时，需要注意的一个关键条件。

导数；单调性；充要条件

1 问题提出

应用函数导数分析函数的单调区间、极值、最值、凸性及拐点，是研究函数图像及其性质的常用方法。由于高中阶段函数导数及其应用既是教学重点也是必考考点，通常考核运用导数研究函数的单调区间、极值等问题。运用函数导数分析函数的单调性，尤其对于严格单调的情形，有一个易错点，下面用一实例说明。

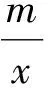
1) 当m=e时，求f(x)的极小值；

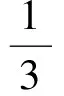
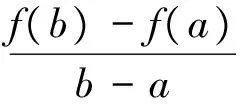
由于此文只讨论导数解决函数单调性的问题，故我们只讨论3)的解答。常见解答(分析法)如下：

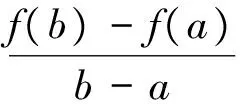
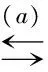
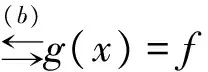
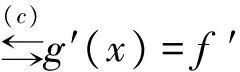
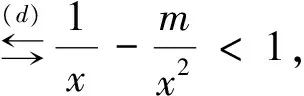
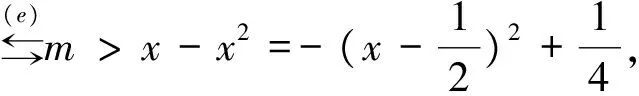
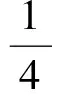
2 问题分析

解决上述问题的本质是用导数解决函数的单调性问题，为此，我们先给出可导函数的导数和函数单调性的关系。

定理1[1]设f(x)在区间I上可导，则f(x)在I上单调递增(减)的充要条件是

f′(x)≥0(f′(x)≤0)

对于严格单调函数，用导数刻画的条件有所变化。

定理2[1]设f(x)在区间I上可导，若f′(x)>0(f′(x)<0)，则f(x)在I上严格单调递增(减)。

然而，定理2的逆命题却不成立。事实上，单个点的导数等于零是不影响严格单调性的。如f(x)=x3在f′(0)=0，f′(x)≥0，∀x∈(-∞,+∞),但f(x)在(-∞,+∞)上严格单调递增。

用导数刻画的严格单调函数的充要条件如下。

定理3[1]设f(x)在区间(a,b)上可导，则f(x)在(a,b)上严格单调递增(减)的充要条件是：

1) 对∀x∈(a,b),f′(x)≥0(f′(x)≤0)；

2) 在区间(a,b)的任何子区间上f′(x)≠0.

3 问题解决

本节根据第2节的定理分析第1节的解答。找出问题所在，给出正确解答。

例1解答中(c)是将函数单调性转化为导数解决，条件给的是严格单调递减，而导数用严格小于零，也就是用了定理2 的逆命题，故第三步出错了。这是用导数解决单调性最容易忽视的一个问题，而本题分析条件，很容易忽视导数中取等的部分，下面给出正确解法。

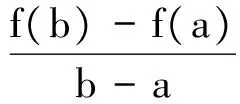
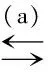
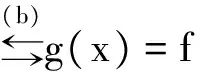
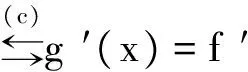
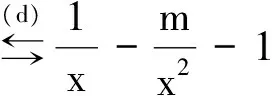
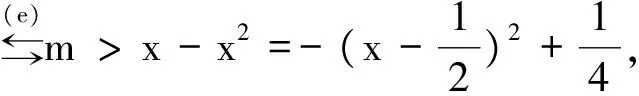
正确解法的关键是第三步，也是易出错的地方，考察的是用导数表示严格单调的充要条件。

关于导数的应用，每年全国各地高考中，必考一道大题(可见历年高考真题)，涉及函数极值最值、单调性(或不等式证明)、零点(或方程的根)个数，曲线的切线等，可见导数应用是高考必考考点，而这些应用中都要考察函数的单调性。从而也是教学研究中常见选题[2～6]。

[1]华东师范大学数学系． 数学分析(第4 版)[M]．北京：高等教育出版社， 2010.

[2]畅佳茹. 有关函数单调性的高考试题的教学研究[D].西安：西北大学,2016.

[3]徐 真. 高中生“导数及其应用”学习策略研究[D].济南：山东师范大学,2015.

[4]刘 璐. 函数单调性及其在高中数学中的应用[D].西安：西北大学,2015.

[5]闫 伟. 高中数学“导数及其应用”教学研究[D].吉林：东北师范大学,2015.

[6]丁明杰. 浅谈导数在高中数学中的应用[J]. 学周刊,2012,(06):122～125.

Anoteonanalysingthemonotonicityoffunctionsbyderivatives

CHEN Yin-lan

(College of Mathematics and Statistics，Hubei Normal University，Huangshi 435002，China)

In this paper, a common wrong answer to the question of function monotonicity in college entrance examination questions is put forward, and the source of error is analyzed. When we analyze the monotonicity of function by derivative, we should notice a key condition.

derivatives;monotonicity;sufficient and necessary conditions

O172.1

A

2096-3149(2017)04- 0083-03

10.3969/j.issn.2096-3149.2017.04.017

2017—05—11

陈引兰(1974— )，女，湖北罗田人，副教授，硕士，主要研究方向为基础数学.