基于标签传递图割的图像分割算法

袁恒东

(南京理工大学 计算机科学与工程学院,江苏 南京 210094)

基于标签传递图割的图像分割算法

袁恒东

(南京理工大学 计算机科学与工程学院,江苏 南京 210094)

基于图割的交互式图像分割方法实现了基于用户感兴趣区域的图像前景和背景分割，在计算机视觉和图像处理领域受到了众多研究者的关注。传统图割算法往往是基于图像局部特征进行分割，其收敛速度以及图像结构描述能力具有一定的局限性。为了进一步提高分割精度，提出一种基于标签传递图割的交互式图像分割算法。首先通过引入三层超像素层构造图模型，实现高层信息的计算。通过多层超像素层，既能抑制过分割，也可以通过不同参数的超像素来增加算法的鲁棒性，提升算法稳定性能。然后结合高次信息，采用已标记样本特征指导未标记样本的标签分配，进行标签传递，利用较少标记样本对未标记样本进行聚类，从而提高了学习精度。最后使用最大流/最小割算法求解最终的分割结果。在MSRC和Berkeley数据集上进行的分割实验表明，基于标签传递和图割的图像分割算法是有效的。

交互式图像分割；图割；超像素；标签传递

0 引 言

目前，图像分割方法主要有基于区域的分割方法和基于边缘的分割方法。基于区域的分割方法是将区域作为处理对象，根据灰度、纹理等将目标分割出来，如高斯混合模型(GMM)，通过图像的特征进行聚类，该类方法易出现过分割现象，无法保证全局最优。基于边缘的分割方法主要依据物体边缘的邻域灰度值不连续、阶越的特性，此类方法依赖初始标记的轮廓线，对初始标记较敏感，易出现局部极值。由BOYKOV等[1]提出的Graph cuts模型，是目前研究和应用最为广泛的交互式图像分割方法之一。该方法在分割过程中将图像的区域信息和边界信息同时引入，先利用图像建图，再求图的最小割，基于图割的图像分割方法可以得到较好的分割效果。

传统的Graph cuts方法基于统计直方图，根据交互的标记信息获得每个像素属于前、背景的概率，但由于直方图的限制，该类方法对低对比度和复杂背景的图像进行分割时往往不能获得满意的结果，并且对交互信息的数量有很大的依赖。后来，ROTHER等[2]利用高斯混合模型代替直方图，提出了Grabcut方法。该方法使用方框圈出前景和背景进行交互，通过迭代更新高斯混合模型中的各项参数来获得更优结果，然而因为使用了迭代求解模式，使得内存开销、运算速度和计算复杂度都受到了很大影响。

基于上述分析，文中提出了一种基于标签传递图割的交互式分割方法。在构图时，加入多层超像素，通过超像素增加高次信息，使用多层来降低超像素对图像分割结果的误分，防止过分割，并且通过不同参数的超像素层结合，提高了算法对不同图像分割的鲁棒性。再通过每个节点迭代传递它的标记信息到近邻，直到全局稳定，结合了局部信息和非局部信息，代替GMM来获得每个像素隶属于前、背景的概率，减少计算时的迭代时间，提升了算法运算速度。

1 基于图割的图像分割算法

给定一个标签集合F，一个图像的像素集合P，图像分割可以看成像素标记(pixel labeling)问题，即给图像中的每个像素点p∈P分配一个标fp∈F。图像分割看成二值标记问题，即F={0,1}，其中1代表前景标签，0代表背景标签[3]。图像分割即为从图像像素集合P到标签集合F进行映射，表示为f={fp|fp∈F}。根据使用者设定的前景种子点和背景点限定的边缘和区域的性质，设计出相对应的能量函数E(f)。能量函数E(f)中一般包括两部分：平滑约束部分和区域约束部分，即E(f)=Esmooth(f)+Eregion(f)，常常把基于图割的交互式图像分割方法的能量函数表达为：

E(f)=R(f)+λ·B(f)=Er(f)+λ·Eb(f)

(1)

其中，Er为区域项，强调数据的一致性；Eb为边界项，强调平滑性[4]；λ为调节参数。

根据原图构建无向图G=(V,E),V代表节点，E代表边缘。图割在无向图G的基础上增加了“源”节点S和“汇”节点T，分别表示前景终点和背景终点。点集V由各像素点以及S、T构成，边集E包括两部分，一部分是每两个相邻节点的连接边n-links(图1右实线)，另一部分是普通节点和终端节点的连接边t-links(图1右虚线)。

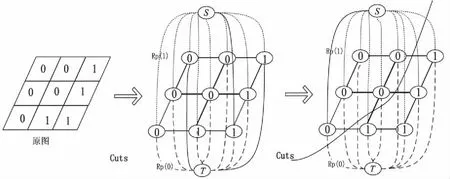
图1 Graph Cuts模型

然后使用最大流/最小割算法求解图的最小割集[5]。割是割集中所有边的权重之和，若一个割中的边权值之和为最小，即最小割，就是图割的结果。由BOYKOV和KOLMOGOROV提出的max-flow/min-cut算法[6]就可以用来获得S-T图的最小割。

由于将多种区域信息与边界信息进行了有效结合，基于图割的图像分割方法的效果要好于只有一种信息进行指导时分割所产生的效果，具有全局最优、数值鲁棒性强等显著优点。传统的基于图割的图像分割算法使用像素点间的相似性表征局部信息，再通过求得的相似性进行图像分割；而目前基于图像非局部信息的改进算法往往是结合区域或者全局信息，利用计算图像中非局部的特征信息，但是仍然存在一定的不足之处：分割算法在使用GMM时采用EM算法，需要迭代收敛，较复杂，时间消耗大;在复杂背景和低对比的图像中，由于分割信息单一，算法往往出现误分割；对于局部信息，独立的像素点间易受到噪声、极值点等的影响，所以在表征其相似性关系时难度较大，从而影响分割，得到错误的分割结果。

2 文中算法

一般图像分割方法在分割过程中只考虑图像的像素信息或局部信息，但在超像素的指导下，结合非局部信息可作为一个重要特征来提升图像的分割质量。

2.1 超像素层权重构造

超像素是指具有某些相似特征的相邻像素构成的不规则像素块。它利用像素之间特征的相似性将像素分类，用少量的超像素代替大量的像素表达图片特征，很大程度上降低了图像处理的复杂度[7-8]。文中采用SLIC(Simple Linear Iterative Cluster)算法生成超像素[9]。SLIC算法产生的超像素紧凑整齐，邻域特征易表达，且设置的参数较少。

由于一些区域可能由于噪声和参数值而仅在一个过分割中与真实对象边界不一致，所以通过不同参数得到多个分割来减少关于区域形状的不确定性。通过将SLIC算法的分割种子点设为400、800、1 600个，使用SLIC分割得到三层超像素层，将每个超像素层中超像素和像素层中像素点连接，从而建立结合了像素层和多重超像素层的图模型，如图2所示。其中，左边是图像右边是图模型，图像由下往上分别是原图和使用了三种不同参数得到的分割图像，右半边展示了文中算法模型的构造和连接方式。

图2 结合多重超像素的图模型

从图2中可以看出，图模型建立完成后图中的边有三种，分别是像素层中像素点之间的连接边lx、超像素层中超像素之间的连接边ly和像素点和超像素间的连接边lxy。对于层节点间的相似性w由欧氏距离计算得到，所以图的邻接矩阵W即为：

(2)

其中，Wxx是像素层内的像素点之间的相似性；Wxy,Wyx是像素层内的像素点与超像素层内的超像素点之间的相似性；Wyy是超像素层内的超像素点之间的相似性。

由于像素层内的像素点之间的相似性、超像素层内的超像素点之间的相似性较高，在计算边的权重时，加入参数α，对于邻接矩阵W，将一般的公式改为：

(3)

2.2 结合标签传递的图割算法

利用局部和全局一致性[10]的学习方法进行标签传递，降低了对标记点数量的依懒性，减少了迭代时间和算法的复杂度，提高了图像的利用率和分割精度。标签传递的核心是对每个点进行反复迭代，传递它的标签信息到它的近邻，直到所有样本标签达到稳定。

ZHOU等[10]对算法的收敛性进行了计算和证明，标注概率F收敛到一个等式：

F*=(I-βS)-1Y

(4)

其中，F*是一个定值，因此它是该迭代算法的固定唯一解，提供了一种无需迭代直接解决问题的方法,节省了计算的时空消耗。

具体的算法步骤如下：

(1)使用SLIC进行预分割，得到三种不同个数的超像素层。

(2)像素层和三层超像素层连接，构造图模型。

由步骤(2)建立的模型计算相似度矩阵，相似度由式(5)得到，再根据式(3)得到邻接矩阵W。

(5)

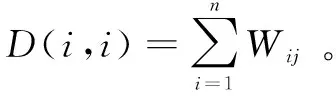
(4)使用式(4)计算每个像素点标签的概率，即文中算法的能量函数为：

E(f)=(I-βS)-1Y+λ·Eb(f)

(6)

(5)使用最大流/最小割优化能量函数，求得能量函数的最小值，也就可得到相同代价的图的割集。

最后在图中去掉割集的所有边，图将会被分割成互不相交的两部分。文中算法通过结合超像素这个高层语义进行权重计算，并且结合局部和全局的一致性进行标签预分配，使得图割算法能够利用全局和高次信息，提高算法的分割精度。

3 实验结果分析与比较

为了进行算法有效性以及正确性的评估，选择了MSRC和Berkeley公共图片库作为实验的图像数据集。采用图像的错误率来评价分割结果，分割错误率定义为错分类像素点的数目与所有未分类像素点数目的比值，其中未分类像素点不包括前、背景的种子点。通过对测试数据集中的50幅测试图像分割后取平均错误率来评价分割结果，在两个测试图像库中做了定量评估。

3.1 参数设置

算法中式(3)的参数α和式(6)的参数β由多组对比实验得到合适的实验值，分别为0.12和0.77。图3是α、β取值过程中的平均分割错误率。三层超像素的K值分别为400、800、1 600。由于文中算法是先确定β值的，所以从图3可以看到，对应的分割错误率比较高。确定策略是β从0到1变化，通过数据比较可知，当β为0.77时，分割的错误率最小，分割的效果最佳。同样，通过固定其他参数，α值在0到1变化时在50幅测试集上的分割错误率表明，当α值为0.12时，分割的错误率最小，分割的效果最佳。

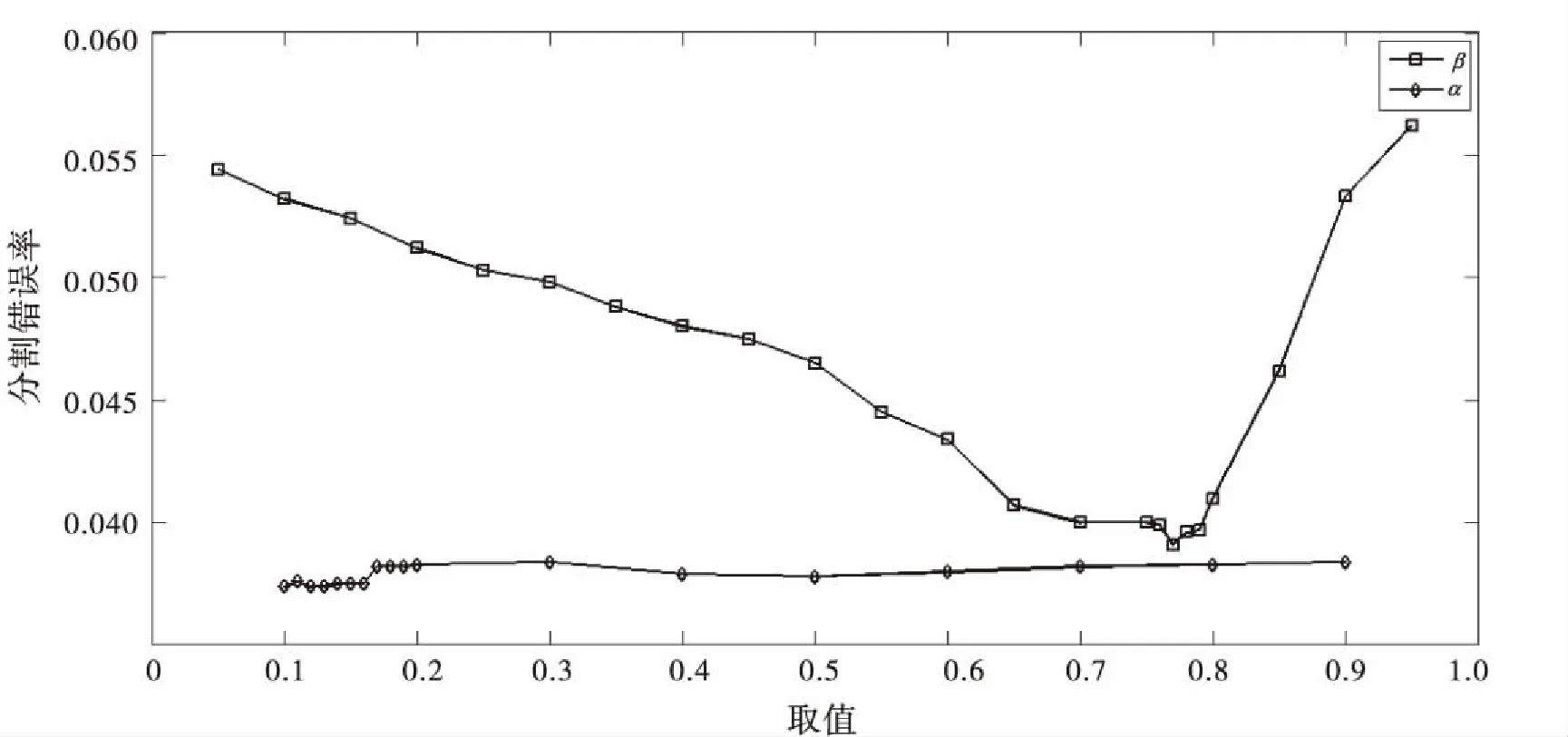
图3 不同α、β取值时的分割错误率

3.2 实验结果分析

将文中算法与传统图割算法(GC)、随机游走算法[11](RW)和无参高阶学习算法[12](NPHO)进行比较。文中算法的分割结果如图4所示，图中是20幅Berkeley图像和30幅MSRC图像分割后的结果。

图4 文中算法的分割结果

图5为每幅图像的分割错误率，从中可以看出文中算法的错误率基本都是最低，证明了基于超像素和标签传递的图割算法的可行性。

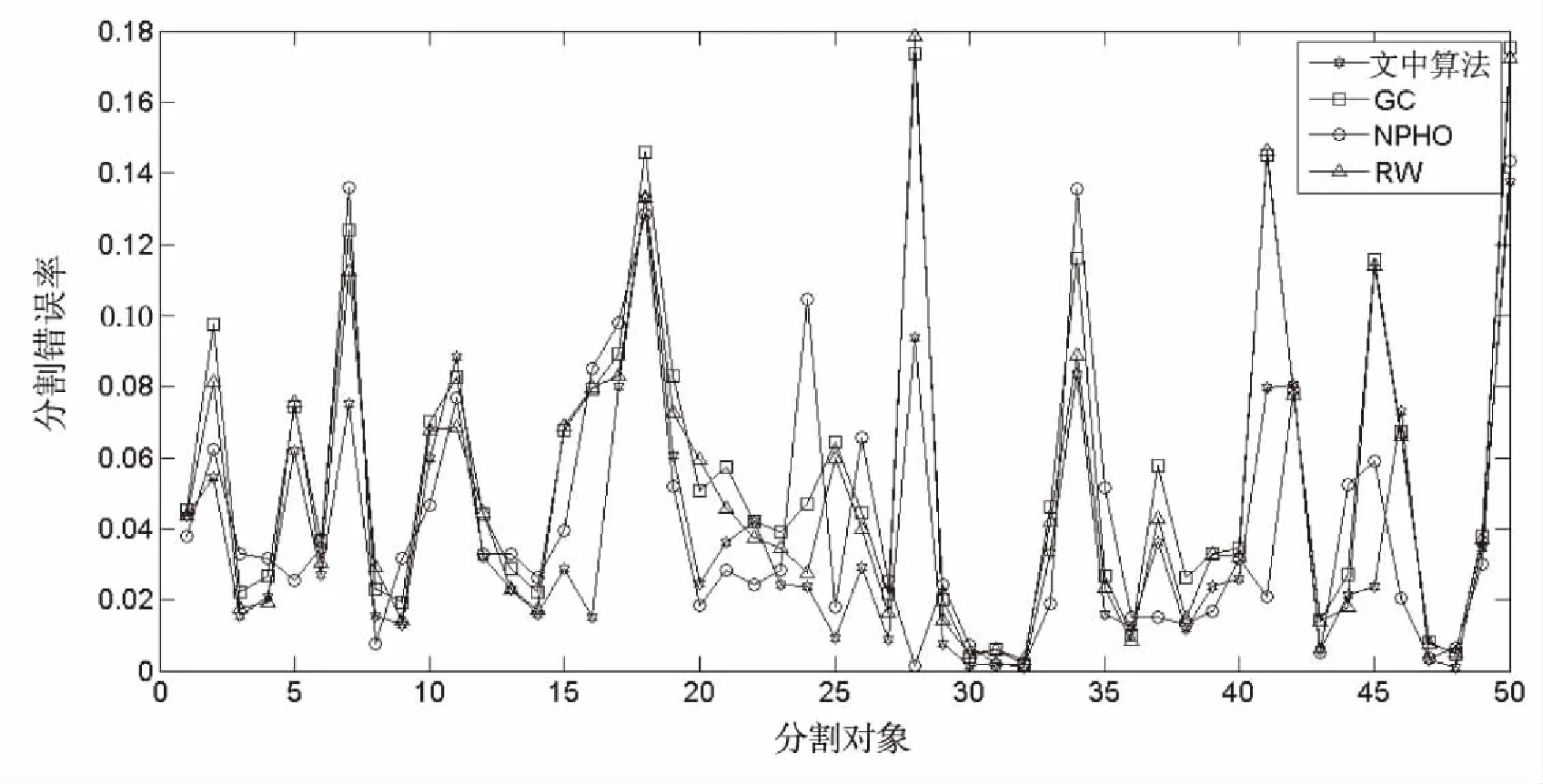
图5 分割错误率对比

表1给出了50幅测试图的平均分割错误率。根据具体实验结果可以发现，文中算法的分割错误率最低，表明该算法的分割效果较好。

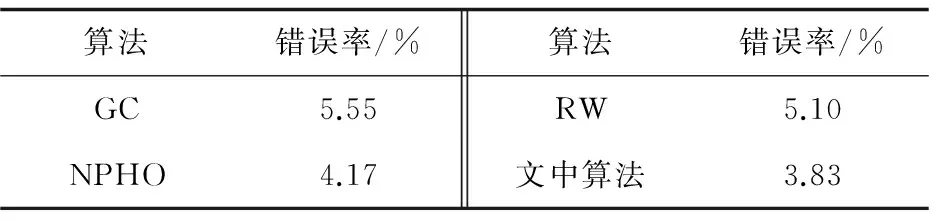
表1 数据集中多个算法的平均分割错误率

4 结束语

文中算法结合了超像素和标签传递，通过在图割算法中加入超像素层，在构图计算权重时考虑到高次信息，再使用标签传递算法，让每个节点反复迭代传递它的标记信息到它的近邻，直到所有样本的标记达到稳定。最后通过多种分割方法的实验比较和定量的分割错误率分析证明了该算法的可行性和有效性。虽然文中算法继承了半监督学习的优点，提高了图像分割的效果，但对于交互信息极少和前背景部分较多融合、对比度低的图像的分割效果不是特别好；另外，使用矩阵存储节点间的相似度，所占用内存空间较大，对于高分辨率图像的数据处理较慢，这些问题还需要在今后的研究中继续进行解决。

[1] BOYKOV Y,JOLLY M P.Interactive graph cuts for optimal boundary & region segmentation of objects in ND images[C]//Eighth IEEE international conference on computer vision.[s.l.]:IEEE,2001:105-112.

[2] ROTHER C,KOLMOGOROV V,BLAKE A."GrabCut":interactive foreground extraction using iterated graph cuts[J].ACM Transactions on Graphics,2004,23(3):309-314.

[3] GREIGD M,PORTEOUS B T,SEHEULT A H.Exact maximum a posteriori estimation for binary images[J].Journal of the Royal Statistical Society,1989,51(2):271-279.

[4] BOYKOV Y,VEKSLER O,ZABIH R.Markov random fields with efficient approximations[C]//Proceedings of IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,1998:648-655.

[5] 刘松涛,殷福亮.基于图割的图像分割方法及其新进展[J].自动化学报,2012,38(6):911-922.

[6] BOYKOV Y,KOLMOGOROV V.An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2004,26(9):1124-1137.

[7] 王春瑶,陈俊周,李 炜.超像素分割算法研究综述[J].计算机应用研究,2014,31(1):6-12.

[8] 韩守东,赵 勇,陶文兵,等.基于高斯超像素的快速Graph Cuts图像分割方法[J].自动化学报,2011,37(1):11-20.

[9] ACHANTA R,SHAJI A,SMITH K,et al.SLIC superpixels[R].[s.l.]:[s.n.],2010.

[10] ZHOU D,BOUSQUET O,LAL T N,et al.Learning with local and global consistency[C]//Proceedings of the 16th international conference on neural information processing systems.Whistler,British Columbia,Canada:MIT Press，2004:321-328.

[11] GRADY L.Random walks for image segmentation[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(11):1768-1783.

[12] KIM T H,LEE K M,SANG U L.Nonparametric higher-order learning for interactive segmentation[C]//Proceedings of international conference of computer vision and pattern recognition.Seoul,South Korea:IEEE,2010:3201-3208.

AnImageSegmentationAlgorithmBasedonLabelPropagationGraphCut

YUAN Heng-dong

(School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

The interactive image segmentation algorithm based on graph cut segments the foreground and background in the image based on the region of interest of the users,and has

the attention of many researchers in the field of computer vision and image processing.Traditional image segmentation algorithm is usually based on local features of image,which is limited to its convergence speed and description of image structure.In order to further improve the segmentation accuracy,an interactive image segmentation algorithm based on label propagation and graph cut is proposed.Firstly,a three-layer super-pixel layer structure graph model is introduced to consider the high-level information,which can further improve its robustness and stability.Then,the label propagation technology is utilized to cluster the unlabeled samples with limited labeled samples and improve the segmentation accuracy by combining the local and high-order information.Finally,the maximum flow/minimum cut algorithm is used to achieve the final segmentation result.Experiments on MSRC and Berkeley datasets demonstrate the effectiveness of the proposed algorithm comparing with state-of-the-art methods.

interactive image segmentation;graph cut;super pixels;label propagation

TP301.6

A

1673-629X(2017)12-0035-04

10.3969/j.issn.1673-629X.2017.12.008

2016-12-30

2017-05-03 < class="emphasis_bold">网络出版时间

时间：2017-09-27

国家自然科学基金资助项目(61401209)；江苏省自然科学基金青年基金项目(BK20140790)；中国博士后科学基金(2014T70525,2013M531364)

袁恒东(1992-)，男，硕士研究生，研究方向为图像分割。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170927.0958.044.html