风力机尾缘襟翼结构参数优化及控制性能分析

张文广， 白雪剑， 韩 越

(1．华北电力大学 新能源电力系统国家重点实验室，北京 102206；2．华北电力大学 工业过程测控新技术与系统北京市重点实验室，北京 102206)

风力机尾缘襟翼结构参数优化及控制性能分析

张文广1， 白雪剑2， 韩 越2

(1．华北电力大学 新能源电力系统国家重点实验室，北京 102206；2．华北电力大学 工业过程测控新技术与系统北京市重点实验室，北京 102206)

为研究适应不同风况下的尾缘襟翼最优结构参数，以NREL 5 MW风力机为参考对象，对FAST进行二次开发，在Matlab/Simulink上搭建了带尾缘襟翼的风力机气动弹性伺服仿真平台；以11.4 m/s稳定风为例，综合考虑尾缘襟翼位置、长度、占弦比及摆角范围对风力机载荷抑制及功率捕获的影响，提出了基于正交设计的大型智能风力机尾缘襟翼的参数优化方法，得到一组最优的尾缘襟翼结构参数；研究了标准湍流风况下尾缘襟翼控制对风力机动态性能的影响.结果表明：尾缘襟翼不仅可显著降低叶片的疲劳载荷、减少变桨机构动作，还可有效抑制风力机输出功率的波动.

大型水平轴风力机； 尾缘襟翼； 正交设计； 载荷抑制； 风力发电控制

随着风力发电技术的发展，风力机的单机功率不断增大，导致叶片尺寸也不断增加.目前，西门子7 MW海上风力机组SWT-7.0-154的叶片长度达到75 m[1].水平轴风力机的大型化加剧了风力机的疲劳载荷和极限载荷，不仅增加了风力机的制造成本和后期的维护费用，还增大了风力机的控制难度.目前，变桨控制技术作为应用于风力机叶片的主动降载技术，由于其只能改变整个叶片的迎风角，且变桨机构惯性较大，无法应对大型叶片的局部载荷和极限载荷波动[2]，不能满足大型风力机(尤其是海上风力机)的需求.因此，智能叶片的概念应运而生.通过主动消减气动力引起的不利振动，智能叶片能够减小风力机疲劳载荷和极限载荷，从而降低风力机的维护费用，并提高风力机运行的可靠性，进而降低风力发电成本[3].目前处于研究阶段的主动降载技术中，尾缘襟翼技术可通过改变翼型来改变叶片的气动性能，具有响应速度快、调节能力强等特点，因此尾缘襟翼技术被认为是最可行的主动降载技术[4].

国内外学者对带尾缘襟翼的大型风力机智能叶片技术进行了一定程度的研究.Castaignet等[5]在Vestas V27型风力机叶片上安装了长为70 cm的尾缘襟翼，并根据38 min的测试数据得出叶片根部载荷平均减少了14%的结论.Berg等[6-7]设计、制造并测试了1个具有主动气动载荷控制设备的风力机转子，研究结果表明尾缘襟翼可有效降低叶片根部的疲劳载荷，但也会在一定程度上减少风力机的功率捕获.郝文星等[8]通过对柔性尾缘襟翼进行参数化建模，采用数值模拟方法研究了尾缘襟翼对翼型整体静态与动态气动性能的影响.祖红亚等[9]以NACA0018为基准翼型，采用Fluent数值模拟方法对比研究了尾缘襟翼相对长度对翼型气动性能的影响.上述研究从理论和实践上验证了尾缘襟翼具有改变气动性能、降低叶片载荷的作用.但有关尾缘襟翼结构参数对增大降载作用、减小功率损失以及风力机动态性能影响，尚没有详细的研究和优化方法.

笔者通过改进FAST，在Matlab/Simulink上搭建了带尾缘襟翼的风力机气动弹性伺服仿真平台，以NREL 5 MW风力机模型为参考对象，以11.4 m/s稳定风为例，使用正交设计法[10]设计了尾缘襟翼结构参数的优化方案，并探究了标准湍流风况下尾缘襟翼控制对风力机动态性能的影响.

1 计算模型

FAST[11]是由美国国家可再生能源实验室(NREL)开发的气动弹性伺服仿真平台，可计算2叶片或3叶片水平轴风力机的疲劳载荷和极限载荷.

1.1 气动性能计算模型

利用FAST对风力机的气动性能进行数值模拟时，主要采用了叶素动量理论模型、动态入流模型及动态失速模型等[11].

叶素动量理论模型分为叶素理论模型和动量理论模型.叶素理论模型是将叶片沿展向分为有限个叶素，对每个叶素进行独立的气动性能分析.动量理论模型是假设风力机流场中的流体与外界没有能量交换，气流总能量保持不变，并采用动量定理计算叶轮从风能中获得的机械能.叶素动量理论模型是理想的空气动力学理论，当诱导因子值较大时需进行葛劳渥特修正[12].为了使计算结果与实际风力机的表现更一致，计算过程中考虑了斜入流修正和叶尖损失修正，进一步提高了静态气动性能的计算精度.

动态入流模型是基于广义动态尾流理论的气动计算模型，考虑了流场从变化到稳定的短暂延迟时间[13].相比叶素动量理论模型，在叶片攻角快速变化时，动态入流模型的计算更加准确.

动态失速模型是基于Beddoes和Leishman研究的半经验模型，考虑了后缘失速、附着流动、前缘分离和可压缩效应，且修正了阻力和力矩系数.Beddoes-Leishman动态失速模型可使叶片挥舞方向的振动计算更加准确[14].

FAST在模拟3叶片水平轴风力机时考虑了24个自由度，计算结果准确度高[11].全球风力发电领域中德国劳氏集团(GL)风能事业部是世界上公认的权威检测认证机构.2005年GL发布了对FAST的检测报告，通过分析比较FAST与GL的DHAT仿真工具仿真得到的3种不同风力机40个输出参数值，认证了FAST是可接受的风力机设计仿真工具[15].笔者使用的计算模型是在FAST基础上搭建的，其计算及仿真结果的可信度较高.

1.2 带尾缘襟翼的风力机气动弹性伺服仿真平台

通过对FAST的二次开发，结合AeroDyn[13]、Turbsim[16]及Xfoil[17]，在Matlab/Simulink上搭建了带尾缘襟翼的风力机气动弹性伺服仿真平台.在该平台上，通过修改Aerodyn输入文件来实现不同尾缘襟翼结构参数下的仿真实验，具体步骤为：

(1)利用Xfoil设计生成指定占弦比和角度的尾缘襟翼翼型，分析其气动性能，并生成翼型气动数据文件.

(2)利用Turbsim建立风场模型文件.

(3)利用Aerodyn输入文件调用风场模型文件及尾缘襟翼翼型气动数据文件，组成指定长度、占弦比及位置的尾缘襟翼叶片文件.

(4)利用FAST调用Aerodyn输入文件，得到尾缘襟翼叶片的气动力数据，计算分析风力机的动态特性.

(5)在所搭建的带尾缘襟翼的风力机气动弹性伺服仿真平台上实现变桨、变速及尾缘襟翼的闭环控制.

1.3 NREL 5 MW风力机

笔者选用的模型为NREL 5 MW 3叶片变速变桨型风力机，其原始叶片总长为61.5 m，由8种翼型组成[18].为方便正交设计，从DU35_A17翼型开始，将叶片分为每段长为2.05 m的叶素，从叶根到叶尖共29段叶素，叶片结构如图1所示.

图1 NREL 5 MW风力机的叶片结构

2 正交设计与分析

由于因子水平数较多，实验规模过大，因此难以进行全面的仿真实验.正交设计是一种可安排多因素实验、寻求最优因子水平组合的高效率实验设计方法，具有整齐可比、均匀分散、简单易行的优点，因此笔者采用正交设计方法进行尾缘襟翼结构参数优化.

2.1 正交设计

2.1.1 仿真实验优化目标

由文献[7]可知，尾缘襟翼可有效降低叶片载荷，但也会一定程度上减少风力机的功率捕获，因此正交设计需综合考虑这两方面因素.仿真实验有2个优化目标：最大程度增大尾缘襟翼在降低叶片载荷方面的作用；最大程度减小尾缘襟翼对风力机输出功率的影响.

2.1.2 仿真实验指标

针对2个优化目标，确定仿真实验指标如下：

(1)最大程度降低叶片载荷，主要指标为叶根挥舞弯矩平均值变化率y1，叶根挥舞弯矩标准偏差变化率y2，叶尖挥舞方向偏移量平均值变化率y3，叶尖挥舞方向偏移量标准偏差变化率y4.

(2)最大程度减小尾缘襟翼对风力机输出功率的影响，主要指标为高速轴功率平均值变化率y5和高速轴功率标准差变化率y6.

2.1.3 仿真因子与因子水平

仿真因子如下：尾缘襟翼的长度A、摆角范围B、占弦比C和位置D.

因子水平如下：长度为9水平(基准长度2.05 m的1～9倍)，摆角范围为4水平(-5°～5°、-10°～10°、-15°～15°、-20°～20°)，占弦比为10水平(5%、10%、…、50%)和位置为20水平(10～29段叶素).

仿真实验中，由于因子水平数较大，不便设计单一的正交分析表，因此采用2次正交设计来进行优化实验.

2.2 第1次正交实验

2.2.1 正交设计

如表1所示，均匀选取因子水平，所需正交设计表为L25(42×52)，可由L25(56)正交表[10]改造得到.正交设计表如表2所示.

表1 第1次正交设计因子水平表

NREL 5 MW风力机的额定风速为11.4 m/s，因此笔者选用11.4 m/s的稳定风况进行300 s无尾缘襟翼仿真实验，考虑到初始阶段存在风力机启机等不稳定过程，取100～300 s数据进行分析，风力机参数见表3.

根据表2进行25次仿真实验，取100～300 s数据进行分析，得到25个叶根挥舞弯矩平均值、叶根挥舞弯矩标准差、叶尖挥舞方向偏移量平均值、叶尖挥舞方向偏移量标准差、高速轴功率平均值和高速轴功率标准差.

(1)

根据式(1)可得到25次仿真实验的6组指标，即叶根挥舞弯矩平均值变化率y1、叶根挥舞弯矩标准差变化率y2、叶尖挥舞方向偏移量平均值变化率y3、叶尖挥舞方向偏移量标准差变化率y4、高速轴功率平均值变化率y5和高速轴功率标准差变化率y6.表4给出了3组仿真实验结果，其余不再赘述.

表2 L25(42×52)正交设计表

表3 无尾缘襟翼时的风力机参数

表4 第1次仿真实验结果

2.2.2 正交分析

根据正交设计的仿真实验结果，采用极差分析、方差分析和综合评分这3种分析方法来获取最优因子水平组合.

(1)极差分析

分别对6组指标进行极差分析，结果见表5.由表5可知，因子D最重要，应取为26；其次是因子A，应取为7；再次是因子B，应取为-20°～20°；最后是因子C，应取为0.2.极差分析的最优因子水平组合为A4B4C2D5.

表5 第1次正交设计极差分析结果

(2)方差分析

分别对6组指标进行方差分析，各仿真因子方差分析F比见表6.

表6 第1次正交设计方差分析F比

各因子自由度fA为3、fB为3、fC为4、fD为4，正交表的自由度fT为24.误差自由度为fe=fT-fA-fB-fC-fD=10.

查阅F分布的0.90分位数表可知，显著性水平为0.1时，F0.90(3,10)=2.73，F0.90(4,10)=2.61.当因子A、因子B、因子C和因子D的F比分别大于2.73、2.73、2.61和2.61时，该指标下仿真因子为显著因子，方差分析结果见表7.由表7可知，方差分析最优因子水平组合为A4B4D5.

(3)综合评分分析

表7 第1次正交设计方差分析结果

将1个因子水平组合下的多个指标综合成为一个指标，称该指标为综合评分指标.在6个指标中，y1、y2、y3、y4越小，表明尾缘襟翼在降低叶片根部疲劳载荷方面的作用越大；y5越大，y6越小，表明尾缘襟翼对风力机输出功率的影响越小，均衡考虑仿真实验优化的2个目标，设计综合评分指标为：

(2)

根据25次仿真实验结果计算可得，第19号的综合评分指标最大，z为0.42，即第19号仿真实验组合(A4B4C2D5)为最优因子水平组合.

综合比较3种分析方法，得到第1次正交设计的最优因子水平组合为A4B4C2D5.尾缘襟翼结构参数分别为：长度为基准长度的7倍，即14.35 m；摆角范围为-20°～20°；占弦比为20%；位置为第26段叶素，即距叶根55.825 m处.

2.3 第2次正交实验

2.3.1 正交设计

在第1次正交设计的基础上，进行第2次正交设计，因子水平如表8所示.

表8 第2次正交设计因子水平表

由表8可知，所需正交设计表为L25(42×52)，将表2表头的长度A与位置D交换位置即可，第2次仿真实验结果如表9所示，表中仅列出3组仿真实验结果，其余不再赘述.

2.3.2 正交分析

极差分析、方差分析和综合评分分析得到的最优因子水平组合分别为A3B4C4D4、A5B4C4D4和A5B3C4D2.对3种最优因子水平组合进行仿真实验，并对其数据进行综合评分分析，结果见表10.由表10可知，最优因子水平组合为A3B4C4D4.

表9 第2次仿真实验结果

表10 第2次正交分析结果

2.4 最优因子水平组合均值估计

为判断正交设计的准确性，需估计出最优因子水平组合均值，并与实际仿真实验结果进行比较.最优因子水平组合均值估计分为点估计和区间估计.

2.4.1 点估计

根据上述统计模型，利用最小二乘法可得到一般平均μ与每个因子水平效应的估计：

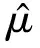
(3)

(4)

类似可得到其他主效应的估计，均为相应参数的无偏估计.根据第2次仿真实验方差分析，y1的显著因子为B和C，最优因子水平组合为B4C4，则：

(5)

(6)

B4C4因子水平组合下，y1均值的无偏估计可取为：

(7)

2.4.2 区间估计

y1,11+4y1,12-y1,13+4y1,14-y1,15+4y1,16-y1,17-y1,18+4y1,19-y1,20-y1,21-y1,22-y1,23+4y1,24+4y1,25)kiy1,i

(8)

(9)

σ2的无偏估计可取为：

(10)

为提高误差方差估计的精度，将不显著因子的平方和并入Se，同时将相应的自由度也并入误差的自由度，即

(11)

(12)

(13)

(14)

(15)

由表11可知，最优因子水平组合A3B4C4D4的6个实际仿真数据指标均在其各自的0.99置信区间内，说明正交分析结果较准确，该因子水平组合满足仿真实验优化目标.

最优尾缘襟翼结构参数分别为：长度为基准长度的7倍，即14.35 m；摆角范围为-20°～20°；占弦比为25%；位置为第26段叶素，即距叶根55.825 m处，位于NACA64_A17翼型段.

表11 最优因子水平组合的各指标置信区间与实际仿真数据

3 标准湍流风况下风力机动态性能

采用上述最优尾缘襟翼结构参数，在轮毂处平均风速为11.4 m/s的湍流风况下进行仿真，并与无尾缘襟翼的仿真结果进行对比，选取100～200 s数据进行分析，结果见表12和表13.

表12 标准湍流风况下风力机参数对比

表13 标准湍流风况下风力机参数的变化率

标准湍流风况下风力机叶片1叶根挥舞弯矩、叶片1叶尖挥舞方向偏移量、高速轴转速、高速轴功率、叶片1桨距角及叶片1尾缘襟翼角的动态曲线如图2～图7所示.

图2 标准湍流风况下叶片1叶根挥舞弯矩的动态曲线

图3 标准湍流风况下叶片1叶尖挥舞方向偏移量的动态曲线

图4 标准湍流风况下高速轴转速的动态曲线

由图2和图3可知，尾缘襟翼控制下叶片1叶根挥舞弯矩及叶片1叶尖挥舞方向偏移量均明显降低.由表13可知，两者平均值分别减少11.13%和34.79%，标准差分别减少33.65%和40.17%，说明在标准湍流风况下，尾缘襟翼控制可有效降低叶片的疲劳载荷.

由图4和图5可知，尾缘襟翼控制下，高速轴转速和高速轴功率的动态超调量均明显降低.由表13可知，其平均值分别减少2.23%和6.74%，标准差分别减少21.69%和23.54%，说明尾缘襟翼控制可使风力机输出功率更平滑，风电场的出力变化更平稳，更利于电网接纳风能.

图5 标准湍流风况下高速轴功率的动态曲线

图6 标准湍流风况下叶片1桨距角的动态曲线

图7 标准湍流风况下叶片1尾缘襟翼角的动态曲线

由图6可知，尾缘襟翼控制作用下叶片1变桨角度明显减小，变桨时间明显缩短.由图7可知，叶片1尾缘襟翼角变化迅速，说明尾缘襟翼控制具有快速、准确的特点，不仅有效地弥补了变桨控制迟钝滞后的缺点，还可减轻变桨机构动作产生的磨损，提高变桨机构寿命.

4 结 论

(1)在11.4 m/s的额定风况下，NREL 5 MW风力机叶片的最优尾缘襟翼结构参数为：长度为14.35 m，摆角范围为-20°～20°，占弦比为25%，位置为距叶根55.825 m处，位于NACA64_A17翼型段.此基于正交设计的尾缘襟翼结构参数优化方法同样适用于选取其他风况下的参数，具有一定的实际参考价值.

(2)标准湍流风况下，尾缘襟翼不仅可显著降低叶片的疲劳载荷，还可有效减弱风力机输出功率的波动，同时也可以减少变桨机构动作，在延长风力机寿命、减弱风力机输出功率波动等方面均有良好的应用前景.

[1] SIEMENS A G. Siemens wind turbine SWT-7.0-154 technical specifications[EB/OL]. (2016)[2016-11-01]. http://www.siemens.com/content/dam/internet/siemens-com/global/market-specific-solutions/wind/data_sheets/data-sheet-wind-turbine-swt-7.0-154.pdf.

[2] BARLAS T K, VAN KUIK G A M. Review of state of the art in smart rotor control research for wind turbines[J].ProgressinAerospaceSciences, 2010, 46(1): 1-27.

[3] BARLAS T K, VAN KUI G A M. State of the art and prospectives of smart rotor control for wind turbines[J].JournalofPhysics:ConferenceSeries, 2007, 75(1): 1-20.

[4] COUCHMAN I, CASTAIGNET D, POULSEN N K, et al. Active load reduction by means of trailing edge flaps on a wind turbine blade[C]//2014AmericanControlConference. Portland, USA: IEEE, 2014.

[5] CASTAIGNET D, BARLAS T, BUHL T, et al. Full-scale test of trailing edge flaps on a vestas V27 wind turbine: active load reduction and system identification[J].WindEnergy, 2014, 17(4): 549-564.

[6] BERG J C, RESOR B R, PAQUETTE J A, et al. Smart wind turbine rotor: design and field test[R]. Albuquerque, USA: Sandia National Laboratories, 2014.

[7] BERG J C, BARONE M F, YODER N C. Smart wind turbine rotor: data analysis and conclusions[R]. Albuquerque, USA: Sandia National Laboratories, 2014.

[8] 郝文星, 叶舟, 丁勤卫, 等. 柔性襟翼对风力机翼型气动性能的影响[J].动力工程学报, 2016, 36(6): 473-479.

HAO Wenxing, YE Zhou, DING Qinwei, et al. Influence of deformable trailing edge flap on aerodynamic performance of the wind turbine airfoil[J].JournalofChineseSocietyPowerEngineering, 2016, 36(6): 473-479.

[9] 祖红亚, 李春, 李润杰, 等. 襟翼相对长度对翼型气动性能的影响[J].动力工程学报, 2015, 35(8): 666-673.

ZU Hongya, LI Chun, LI Runjie, et al. Effect of relative flap length on aerodynamic performance of the airfoil[J].JournalofChineseSocietyofPowerEngineering, 2015, 35(8): 666-673.

[10] 茆诗松, 周纪芗, 陈颖. 试验设计[M]. 2版. 北京: 中国统计出版社, 2012: 107-185.

[11] JONKMAN J M, BUHL J M L. FAST user's guide[R]. USA: National Renewable Energy Laboratory,2005.

[12] HANSEN M O L. Aerodynamics of wind turbines[M]. 2nd ed. Oxford, U K: Eathscan, 2008: 45-62.

[13] DAVID J L, HANSEN A C. User's guide to the wind turbine aerodynamics computer software aerodyn[R]. USA: Technical Report, 2002.

[14] LEISHMAN J G, BEDDOES T S. A semi-empirical model for dynamic stall[J].JournaloftheAmericanHelicoptersociety, 1989, 34(3): 3-17.

[15] MANJOCK A. Design codes FAST and ADAMS for load calculations of onshore wind turbines[R]. USA: National Renewable Energy Laboratory, 2005.

[16] JONKMAN B J, KILCHER L. TurbSim user's guide: version 1.06.00[R]. USA: National Renewable Energy Laboratory, 2012.

[17] DRELA M, YOUNGREN. XFOIL 6.9 user primer[EB/OL]. (2001)[2016-11-01]. http://web.mit.edu/drela/Public/web/xfoil/xfoil_doc.txt.

[18] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5 MW reference wind turbine for offshore system development[R]. USA: National Renewable Energy Laboratory, 2009.

TrailingEdgeFlapStructureParametersOptimizationofaWindTurbineandAnalysisoftheControlPerformance

ZHANGWenguang1,BAIXuejian2,HANYue2
(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China; 2. Beijing Key Laboratory of New Technology and System on Measuring and Control for Industrial Process, North China Electric Power University, Beijing 102206, China)

To find the optimal structure parameters of trailing edge flaps (TEF) under different wind conditions, an aero-servo-elasticity wind turbine simulation platform was set up on Matlab/Simulink with secondarily developed FAST by taking the NREL 5 MW reference wind turbine as an object of study. Under 11.4 m/s steady wind condition, considering the effects of position, length, chord length ratio and angle range of TEF on load suppression and power capture of the wind turbine, an optimization scheme of TEF parameters was introduced based on orthogonal design method, and a group of optimal parameters were thus obtained. Moreover, the effects of TEF control on wind turbine dynamic properties were explored under standard turbulent wind condition. Results show that the TEF can not only significantly alleviate the fatigue load and reduce the action of pitch mechanism, but also effectively weaken the fluctuation of wind turbine power output.

large-scale horizontal axis wind turbine; trailing edge flap; orthogonal design; load suppression; wind power control

2016-11-16

2017-01-04

国家重点基础研究发展计划(973计划)资助项目(2012CB215203)

张文广(1975-)，男，副教授，博士，主要从事风力机振动检测及主动控制方面的研究.电话(Tel．)：010-61772843；E-mail：zwg@ncepu.edu.cn.

1674-7607(2017)12-1023-08

TK83

A

470.30