基于有限元和神经网络方法对220 kV盆式绝缘子屏蔽罩结构优化设计

淡淑恒，吴 娜，姜 腾，李昊东，高 鹏，朱 锋，王洪信

（1.上海电力学院电气工程学院，上海200090；2.国网淄博供电公司，山东 淄博 255000；3.国网日照供电公司，山东 日照276826）

基于有限元和神经网络方法对220 kV盆式绝缘子屏蔽罩结构优化设计

淡淑恒1，吴 娜1，姜 腾2，李昊东3，高 鹏2，朱 锋2，王洪信2

（1.上海电力学院电气工程学院，上海200090；2.国网淄博供电公司，山东 淄博 255000；3.国网日照供电公司，山东 日照276826）

针对GIS中盆式绝缘子，提出了一种优化其屏蔽罩结构参数的方法。这种方法首先运用有限元方法对盆式绝缘子建立模型，并进行电场计算，然后以此确定了盆式绝缘子屏蔽罩结构优化目标；在此基础上，引入神经网络算法，利用BP神经网络拟合了屏蔽罩各结构参数与优化目标之间的关系，对屏蔽罩的结构参数进行了优化设计，得到最优结构参数，克服了传统穷举法计算量大、消耗时间长的缺点。实验结果表明，安装优化后的屏蔽罩，可以大大降低盆式绝缘子沿面最大场强，有效改善盆式绝缘子沿面电场不均匀程度。

盆式绝缘子；电场计算；屏蔽罩；优化设计；有限元法；神经网络算法

0 引言

气体绝缘组合电器设备GIS（gis insulated switch-gear），即由母线、断路器、互感器、接地开关等组成，这些设备全部封闭在金属接地外壳中，内部不采用空气而用具有优异绝缘和灭弧性能的SF6气体作为绝缘介质的全封闭组合电器，故也称为SF6全封闭组合电器。跟常规敞开式高压配电设备相比，GIS占地面积更小、结构更紧凑、更为可靠、安全、灵活和环保。因此，近年来在超高压和特高压变电站中得到了广泛的应用。在GIS的连接母线中，盆式绝缘子具有支撑导体、隔离气室和电气绝缘等至关重要的作用[1-3]。因此，在对盆式绝缘子进行设计时，要充分考虑绝缘子的沿面电场分布。当绝缘子的沿面场强超过起晕场强时，将会产生电晕放电[4]。

目前，在盆式绝缘子上安装屏蔽罩可有效改善绝缘子沿面电场和电位分布[5-6]。盆式绝缘子的沿面电场受屏蔽罩的形状、尺寸和位置等影响，因此安装合适的屏蔽罩可以有效改善盆式绝缘子沿面电场和电位，减少电晕、闪络现象。但是，并非任何尺寸和位置的屏蔽罩都能降低盆式绝缘子的沿面电场强度，如果设计的不合理，不但不能起到均压的作用，反而会适得其反，导致绝缘性能的下降。因此，对盆式绝缘子屏蔽罩的结构参数进行优化设计具有及其重要的研究意义。

早期的文献一般采用穷举优化方法对屏蔽罩结构进行优化设计，穷举法虽然简单，但是需要不断调整屏蔽罩的结构参数，计算量很大，耗时冗长，人工操作繁杂。近年来，一些学者使用人工智能算法对盆式绝缘子进行优化设计，取得了不错的效果。文献[7]将绝缘子的沿面场强最大值作为目标函数，使用遗传算法对特高压复合绝缘子均压环结构进行优化，得到了最佳参数；文献[8]和文献[9]利用有限元和神经网络遗传算法，将复合绝缘子沿面场强作为目标函数，对均压环结构参数进行优化，得到了均压环结构参数最优解；文献[10]采用有限元和粒子群算法对复合绝缘子均压环结构进行优化设计，得到了优化结构参数；文献[11]采用有限元和遗传算法对盆式绝缘子屏蔽罩形状进行优化，得到优化结构参数，该方法对优化屏蔽罩结构具有参考意义。这些文献基本上都是对复合绝缘子均压环结构进行优化，而对盆式绝缘子屏蔽罩结构进行优化设计的研究较少。

因此，笔者以220 kV盆式绝缘子为研究对象，从以下几方面开展研究工作：

1）利用有限元电磁分析软件Ansoft，按照盆式绝缘子的实际尺寸建立模型，对电位和电场分布进行数值计算，初步分析盆式绝缘子的电位和沿面电场分布；2）针对盆式绝缘子屏蔽罩结构参数，分析各参数对绝缘子沿面电场分布的影响；3）利用神经网络算法，以盆式绝缘子沿面最大场强和屏蔽罩表面最大场强作为目标函数，对屏蔽罩的结构参数进行优化设计。

1 计算模型的建立

1.1 有限元基本理论

所谓有限元法，就是将整个求解区域分成很多很小的子区域，然后对这些子区域应用求解边界问题的原理，对每个小区域进行求解，最后将各个小区域的求解结果和起来得到整个区域的解。有限元法因其理论依据的普遍性，作为一种声誉很高的数值计算方法，已经被广泛应用并成功解决各种许多工程领域中的问题[12]。

利用有限元法，可将无限域问题转变为有限域问题，盆式绝缘子的电场和电位分布最终可看成是下列问题的解[13]。

在求解域内：

在不同介质的交界面上

导体侧电位

有限边界电位

在人工截断边界上

式中：ρ为自由电荷密度；E为求解域内的电场强度；ε0、εr分别为真空介电常数和介质的相对介电常数；n为垂直于分界面的法向量；D1、D2分别为分界面两侧介质内垂直于介质分界面的电位移；V为导体侧具体电位值，本文中V为220 kV；φ为电位，P为位置矢量，f（P）和 h（P）为一般函数，文中采用默认边界条件 f（P）和 h（P）为零。

1.2 盆式绝缘子有限元模型

GIS中盆式绝缘子中心导体连接母线，导通电流。盆式绝缘子盆子由粘接强度优异、介电性能良好的环氧树脂浇注而成，分为凸面和凹面。绝缘子外缘处用法兰和螺栓固定，连接筒壁并接地。母线和筒壁之间充满具有良好电气绝缘性能及优异灭弧性能的SF6气体见图1。

笔者根据盆式绝缘子的实际物理模型和尺寸，建立了盆式绝缘子的计算模型，如图1所示。计算选取的GIS轴向距离600 mm，最大径向距离385 mm；盆子轴向尺寸132mm，法兰厚度18mm，外径220mm；筒壁厚度为10 mm。笔者采用矩形人工边界将无限域截为有限域，在ab和cd上采用Balloon边界条件处理无限远处的边值问题。计算时母线加载电压为220 kV，筒壁电位为0。在盆式绝缘子的计算模型中，各介质的相对介电常数如表1所示。

图1 带屏蔽罩盆式绝缘子计算模型Fig.1 Computational model of basin-type insulator with shielding electrode

表1 电场计算模型中各介质的材料特性Table 1 Properties of different media of the electric field computational model

2 电场和电位计算结果及分析

根据前面建立的盆式绝缘子有限元模型，进行数值计算得到盆式绝缘子的电位和电场分布云图，如图2、3、4 所示。

从图2可以看出，该模型的电位等势线与实际预想的结果一致，所以该计算模型和计算结果具有足够的可信度；图3为无屏蔽罩和有屏蔽罩两种情况下盆式绝缘子沿面电位分布比较，从图中可以看出，安装屏蔽罩可以有效改善盆式绝缘子沿面电位分布。从图4可以看出，由于两种介质的相对介电常数相差较大，因此在两种介质的交界面处电场强度畸变较大。各关键部位最大电场强度值见表2。通过比较无屏蔽罩和有屏蔽罩两种情况下的电场分布，可以发现，1）安装屏蔽罩的盆式绝缘子沿面电场分布大大改善，分布更加均匀，且绝缘子的最大电场强度值得到降低；2）上屏蔽罩可以有效改善绝缘子凸面场强分布，下屏蔽罩可以有效改善绝缘子凹面场强分布；3）上屏蔽罩上的最大场强较小，下屏蔽罩上的最大场强较大。

对比无屏蔽罩和有屏蔽罩两种情况下场强分布结果表明，安装屏蔽罩可以有效改善盆式绝缘子的电位和沿面电场。同时，安装不同结构的屏蔽罩，会呈现出不同的电场分布[11]。鉴于上屏蔽罩的结构变化对绝缘子凸面场强分布影响较小，而下屏蔽罩的结构变化对绝缘子凹面场强分布影响很大。因此，有必要对盆式绝缘子下屏蔽罩的结构进行优化，找到最佳结构参数，以达到最优的均压效果。

图2 盆式绝缘子整体电位分布Fig.2 Potential distribution of basin-type insulator

图3 屏蔽罩对盆式绝缘子电位分布的影响Fig.3 Effect of shielding electrode on potential distribution of basin-type insulator

3 屏蔽罩结构优化

3.1 基于神经网络算法的优化方法

为了得到屏蔽罩最佳结构参数，获得最好的均压效果，需要找到盆式绝缘子凹面最大场强和下屏蔽罩各个参数之间的函数关系。但是盆式绝缘子凹面最大电场强度和下屏蔽罩结构参数不是单调函数的关系，实际上这种关系并不明确，这就使得优化目标函数变得比较复杂。因此，要用一种更为有效可靠的方法将输入变量和目标函数联系起来。

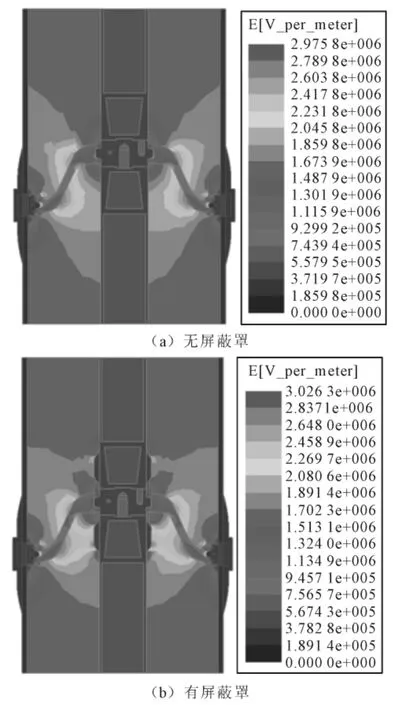
图4 盆式绝缘子整体电场分布Fig.4 The distribution of electric field intensity of the basin-type insulator

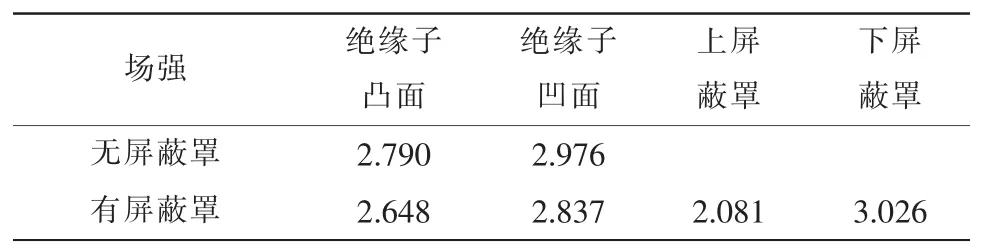
表2 关键部位最大场强Table 2 Maximum electric field intensity of crucial parts kV/mm

近年来，神经网络算法由于具有很强的非线性映射能力，在理论上可以逼近任意函数，因而被应用于许多工程领域。神经网络不需要对具体模型进行透彻的了解，只需要训练少量的样本数据就能达到输入输出之间的多维非线性映射关系。

本文在对下屏蔽罩进行优化设计时，以下屏蔽罩结构参数为输入变量，以盆式绝缘子凹面最大电场强度和下屏蔽罩表面最大电场强度为目标函数，建立他们之间的一种映射关系，即

式中：r、h、l分别为下屏蔽罩的厚度、罩宽和罩深，如图5所示；E1和E2分别为盆式绝缘子凹面最大场强和下屏蔽罩表面最大场强。

图5 下屏蔽罩结构参数Fig.5 The structural parameters of lower shielding electrode

屏蔽罩优化设计的基本思想就是求得一组结构参数r、h和l的值，使得屏蔽罩表面最大场强小于屏蔽罩起始电晕场强的前提下，即

盆式绝缘子凹面最大场强取得最小值，即

笔者提出的基于神经网络优化方法首先利用有限元方法计算得到一些样本数据，提供给神经网络学习训练，建立场强 E1、E2和屏蔽罩结构参数 r、h、l之间的映射关系，再由建立的神经网络模型计算出约定范围内的r、h、l对应的E1和E2，从中找到最优的屏蔽罩结构参数。

3.2 屏蔽罩结构优化神经网络模型

BP神经网络是目前应用最广泛的神经网络模型之一。BP网络是一种按误差传播算法训练的多层前馈网络，能学习训练大量的输入输出映射关系。本文采用最常用的BP神经网络[12-16]，建立图6所示的屏蔽罩结构优化神经网络模型。该模型中屏蔽罩结构参数 r、h 和 l为输入向量，ω1、ω2和 ωn为权系数，盆式绝缘子凹面最大场强E1和下屏蔽罩表面最大场强E2为输出向量。

图6 屏蔽罩结构优化神经网络模型Fig.6 Optimization of the neural network model for the shielding electrode design

神经网络应选取无量纲的向量作为网络的输入向量和输出向量，因而须对屏蔽罩结构参数r、h、l和场强E1、Eh进行[0，1]标准化处理，标准化处理方式如下：

式中：x为参数当前值；x'为当前值映射到区间[0，1]中的值。作为输入向量的屏蔽罩各结构参数变化范围[xmin，xmax]如表3所示。

表3 屏蔽罩结构参数变化区间Table 3 The interval of the structural parameters of the shielding electrode

BP神经网络模型包括输入层、隐含层和输出层。当样本集确定之后，输入层和输出层神经元的个数也随之确定。而隐含层神经元个数的选取是一个难点，隐含层神经元个数如果过少，则神经网络不具有必要的学习能力，如果过多，则容易陷入局部极小点。根据文献[17]提出的经验公式选取隐含层神经元的个数，计算公式如下：

式中：s为隐含层节点数；m为输入层节点数；n为输出层节点数。因此，本文隐含层节点数为4。

输入层的输入和输出都是样本集的属性值，隐含层和输出层的输入

式中：ωij是单元i和单元j之间的权值；xi是单元i的输出；θj是单元j的阈值。

神经网络隐含层和输出层的输出由激活函数得到，本文使用（0，1）内连续取值的Sigmoid函数作为激活函数，神经元的输出为

BP神经网络的主要目的是反复修正权值和阈值，使得误差函数值达到最小。误差函数为

式中：dj为输出层的期望结果，yj为输出层的实际结果。

笔者采用LM算法作为网络的训练算法。根据文献[18]，跟传统的梯度下降法相比LM算法具有明显的速度优势。算法的训练次数为50，学习率为0.01，误差指标为0.001。

训练好的神经网络可以得到屏蔽罩结构参数r、h、l和场强 E1、E2之间的映射关系，根据输入的屏蔽罩结构参数变化区间，输出最优结构参数。

3.3 屏蔽罩结构优化结果

利用训练完成的神经网络对输入的屏蔽罩各结构参数以1mm为步长进行计算，找到E2小于24kV/mm的情况下，E1取最小值时屏蔽罩的结构参数，即为最佳结构参数。通过计算最终得到屏蔽罩的最佳结构参数为r=10 mm、h=50 mm、l=35 mm。根据得到的最优结构参数，修改计算模型，重新计算，将优化前后盆式绝缘子的沿面电场分布进行比较。凸面电场强度计算结果对比情况如图7所示，凹面电场强度计算结果对比情况如图8所示。图中曲线1为优化前的结果，曲线2为优化后的结果。图7中横坐标为从导体侧到筒壁侧沿盆式绝缘子凸面的沿面距离，纵坐标为电场强度。图8中横坐标为从导体侧到筒壁侧沿盆式绝缘子凹面的沿面距离，纵坐标为电场强度。

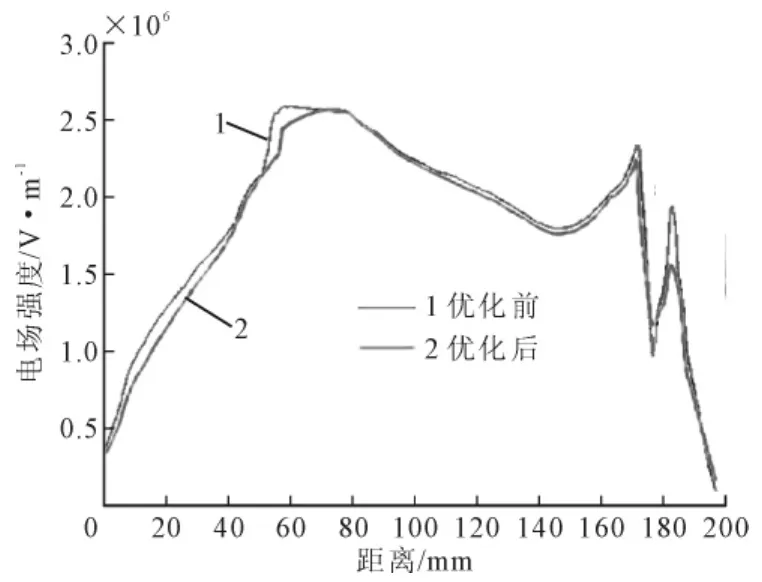
图7 优化前后盆式绝缘子凸面电场分布曲线Fig.7 The distribution of electric field intensity of basin-typeinsulator pre and post optimization（against the cone）

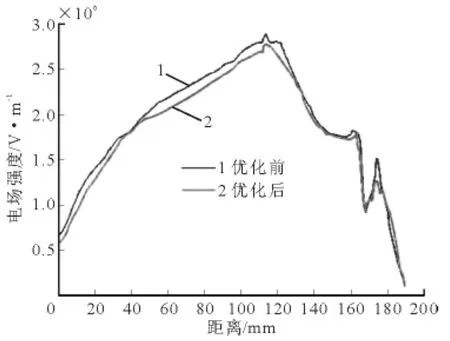
图8 优化前后盆式绝缘子凹面电场分布曲线Fig.8 The distribution of electric field intensity of basin-type insulator pre and post optimization（in the cone）

由优化前后盆式绝缘子凸面和凹面电场强度对比可知，优化后盆式绝缘子沿面电场分布的均匀程度得到很大的改善，从而降低了盆式绝缘子局部放电量和沿面闪络的几率。实验结果表明，优化效果良好。

4 结论

1）对220 kV盆式绝缘子建立仿真模型，进行电场计算，得到各关键部位最大场强，各场强值均在允许范围内，符合基本要求。

2）上屏蔽罩可有效改善绝缘子凸面场强分布，下屏蔽罩可有效改善绝缘子凹面场强分布。

3）盆式绝缘子表明电场强度较高，凹面的最大场强高于凸面，裕度较小。下屏蔽罩结构变化对绝缘子凹面场强影响很大，因此可以通过优化下屏蔽罩的结构参数来改善绝缘子凹面场强分布。

4）利用BP神经网络算法对屏蔽罩各个结构参数进行优化，得到屏蔽罩最优结构参数为r=10 mm、h=50 mm、l=35 mm。加装优化后的屏蔽罩可以大大降低凹面最大场强，有效改善沿面电场分布的均匀程度，优化效果良好。

[1]吴光亚.我国绝缘子的发展现状及应考虑的问题[J].电磁避雷器，2010（2）：7-11.WU Guangya.Development of china’s insulator and the issue should be considered[J].Insulators and Surge Arresters[J]，2010（2）：7-11.

[2]许建存，卢鹏.1 100 kVGIS盆式绝缘子的性能[J].电力建设，2010，31（8）：91-93.XU Jianchun，LU Peng.Performance of the disc-type insulator for 1 100 kV GIS[J].Electric Power Construction，2010，31（8）：91-93.

[3]周浩，朱甜.三种绝缘子性能及其在特高压线路应用研究[J]．电瓷避雷器，2007（217）：7-13.ZHOU Hao，ZHU Tian.Characteristics of three kinds of insulators and their applications evaluation at them in UHV transmission lines[J].Insulators and Surge Arresters，2007（217）：7-13.

[4]卢明，杨庆，阎东，等.复合绝缘子伞群结构对电场分布的影响[J].电瓷避雷器，2011（1）：1-6.LU Ming，YANG Qing，YAN Dong，et al.The effect of the composite insulators sheds type structure on the electric field distributions[J].Insulators and Surge Arresters，2011（1）：1-6.

[5]马爱清，杨秀，陆鑫淼，等.GIS盘式绝缘子三维电场计算及其逆问题分析[J].高电压技术，2010，36（5）：1217-1221.MA Aiqing，YANG Xiu，LU Xinmiao，et al.3D Electric field calculation and Its inverse problem analysis of disktype insulator in GIS[J].High Voltage Engineering，2010，36（5）：1217-1221.

[6]徐建源，汪枫，林莘，等.盆式绝缘子内导体及绝缘子表面形状对电场的影响[J].沈阳工业大学学报，1999，21（5）：405-408.XU Jianyuan，WANG Feng，LIN Shen，et al.Influences of electrode and surface structure of disc insulator on distribution of electric field in GIS[J].Journal of Shenyang U-niversity of Technology，1999，21（5）：405-408.

[7]黄 玲，文习山，蓝 磊，等.基于改进遗传算法的特高压绝缘子均压环优化[J].高电压技术，2009，35（2）：218-224.HUANG Ling，WEN Xishan，LAN Lei，et al.Optimization of grading rings for UHV composite insulator by the improved GA[J].High Voltage Engineering，2009，35（2）：218-224.

[8]司马文霞，杨 庆，孙才新，等.基于有限元和神经网络方法对超高压合成绝缘子均压环结构优化的研究[J].中国电机工程学报，2005，25（17）：115-120.SIMA Wenxia，YANG Qing，SUN Caixin，et al.Optimization of corona ring design dor EHV composite insulator using finite element and neural network method[J].Proceedings of CSEE，2005，25（17）：115-120.

[9]司马文霞，施 健，袁 涛，等.特高压复合绝缘子电场计算及基于神经网络遗传算法的均压环结构优化设计[J].高电压技术，2012，38（2）：257-265.SIMA Wenxia，SHI Jian，YUAN Tao，et al.Electric Field Calculation of Ultra High Voltage Composite Insulator and Optimization Design of Corona Ring Structure Based on Neural Network and Genetic Algorithm[J].High Voltage Engineering，2012，38（2）：257-265.

[10]张施令，胡 伟，彭宗仁，等.采用有限元和粒子群算法优化特高压复合绝缘子均压环结构[J].高电压技术，2012，38（2）：359-367.ZHANG Shiling，HU Wei，PENG Zongren，et al.Structural Optimization of Grading Ring for Ultra High Voltage Composite Insulator by Combining Finite Element Method and Particle Swarm Optimization Algorithm[J].High Voltage Engineering，2012，38（2）：359-367.

[11]杜进桥，张施令，李乃一，等.特高压交流盆式绝缘子电场分布计算及屏蔽罩结构优化[J].高电压技术，2013，39（12）：3037-3043.DU Jinqiao，ZHANG Shiling，LI Naiyi，et al.Electric Field Distribution Calculation and Shielding Electrode Structure Optimization of UHV AC Basin-type Insulator[J].High Voltage Engineering，2013，39（12）：3037-3043.

[12]成俊奇，丁立建.绝缘子表面电场分布的数值仿真[J].电瓷避雷器，2009（6）：16-18.CHENG Junqi，DING Lijian.Numerical simulation of electric field distribution of insulator surface[J].Insulators and Surge Arresters，2009（6）：16-18.

[13]马西奎，冯慈璋.工程电磁场导论[M].北京：机械工业出版社，2008.MA Xikui，FENG Cizhang.Engineering electromagnetic field[M].Beijing，China：Higher Education Press，2008.

[14]谢开贵，李春燕，周家启.基于神经网络的负荷组合预测模型研究[J].中国电机工程学报，2002，22（7）：85－89.Xie Kaigui，Li Chunyan，Zhou Jiaqi.Research of the combination forecasting model for load based on artificial neural network[J].Proceedings of CSEE.2002，22（7）：85－89.

[15]Ahmad A S，Ghosh P S，Aljunid S A K，et al.Modeling of various meteorological effects on contamination level for suspension type of high voltage insulators using ANN[C].Transmission and Distribution Conference and Exhibition 2002，Asia Pacific，IEEE/PES，2002，2：6－10.

[16]张国江，邱家驹，李继红.基于人工神经网络的电力负荷坏数据辨识与调整[J].中国电机工程学报，2001，21（8）：104－107.Zhang Guojiang，Qiu Jiaju，Li Jihong.Outlier identification and justification based on neural network[J].Proceedings of CSEE，2001，21（8）：104－107.

[17]高大启.有教师的线性基本函数前向三层神经网络结构研究[J].计算机学报，1998，21（1）：80－86.GAO Daqi.On Structures of Supervised Linear Basis Function Feed forward Three－Layered Neural Networks[J].Chinese Computers，1998，21（1）：80－86.

[18]HAGAN M T，MENHAI M B.Training feed forward networks with the Marquardt algorithm[J].IEEE Transactions on Neural Networks，1994，5（6）：983－993.

Optimization of Shielding Electrode Design for 220 kV Basin-Type Insulator by Finite Element Method and Neural Network Method

DAN Shuheng1，WU Na1，JIANG Teng2，LI Haodong3，GAO Peng2，ZHU Feng2，WANG Hongxin2
（1.College of Electrical Engineering，Shanghai University of Electric Power，Shanghai 200090，China；2.State Grid Zibo Power Supply Company，Zibo 255000，China；3.State Grid Rizhao Power Supply Company，Rizhao 276826，China）

An approach to optimize the structure parameters of the shielding electrode is proposed for basin-typeinsulatorsinGIS.Firstly，this method establishes a model for basin-type insulators and calculates the electric field by the finite element method.Basing on the calculation results of the model，the BP neural network method is introduced to optimize the structural parameters of shielding electrode.In addition，the highly nonlinear mapping capability of neural network is used to fit the functional relationship between the shielding electrode structure parameters and optimization goal，which avoiding the problem of intensive calculation and tedious time consumption caused by the exhaustion method.The results show that，installing optimized shielding electrode can not only greatly lower the maximum value of surface electrical field，but also apparently improve the surface electrical field distribution of the basin-type insulators.

basin-type insulator；calculation of electric field；shielding electrode；design optimization；finite element method；neural network algorithm

10.16188/j.isa.1003-8337.2017.03.030

2016-03-26

淡淑恒（1969—），女，教授，主要从事新型电气设备的机理研究及研制、电场和磁场的计算分析、盆式绝缘子的设计等方面研究。

上海绿色能源并网工程技术研究中心（编号：13DZ2251900）。