维护条件下产品寿命分布规律分析

李大伟，方 勇，孙 兴

（解放军91550部队，辽宁 大连 116023）

维护条件下产品寿命分布规律分析

李大伟，方 勇，孙 兴

（解放军91550部队，辽宁 大连 116023）

为了掌握维护条件下产品寿命分布规律，进一步解释其失效特性，从维护条件下产品性能状态变化角度出发，结合累积失效理论，利用复合Poisson过程建立了可靠性模型，得到了该条件下产品在线寿命分布模型。在此基础上，建立了维护条件下产品总体寿命分布模型，并利用偏度-峰度系数和贴近度分析，对维护条件下产品在线寿命分布和总体寿命分布规律进行了数值计算，解释了工程产品在线往往具有集中失效，而总体又具有随机失效的特性。以水泵转子为研究对象，通过数值分析，较好地描述了其定期维护条件下的可靠度和寿命分布，进一步验证了模型的可行性。

寿命分布，维护性能，可靠性模型复合，Poisson过程

0 引言

维护是使产品保持规定状态所采取的措施，如润滑、调整和清洁等，也可称为保养［1］。工程中，维护活动相对大型维修较为便捷、费用较低，且可以有效地保持产品的性能可靠性水平，所以越来越多的产品在使用过程中采取定期维护保养活动，如仪表定期校正、机械齿轮定期润滑等［2］。鉴于维护的普遍性和重要性，开展维护条件下产品的寿命分布规律研究，有利于掌握该条件下产品可靠性规律和制定维修策略，具有一定的理论意义和工程价值［3-4］。

随着人们对失效过程的深入认识，国内外学者进行了大量研究，从多个角度建立了产品性能状态和可靠性规律之间的关系。比如经典的Pairs模型，能够较好地描述产品疲劳失效与时间的关系，该模型已应用于裂缝增长数据［5］。文献［6］利用非线性回归方法成功处理了化学涂层的加速性能退化试验数据。文献［7-8］利用Gamma过程分别描述了某型发动机和水泵系统等产品的性能可靠性规律，文献［9］利用Poisson过程建立了金属滑膜的性能可靠性模型，文献［10-11］分别利用布朗运动和几何过程对产品可靠性规律进行了描述。尽管上述方法在工程中得到了较为广泛的应用，但是对象主要是产品自身规律，较少考虑有维护活动参与条件下的产品。同时，通过分析工程产品可靠性规律，能够发现同一批次产品往往表现为集中失效的特性，而多批次产品又具有随机失效的特性，二者具有一定的差异性［12-13］。因此，需要在研究其性能可靠性模型基础上，对产品的寿命分布规律进行研究，以进一步解释产品的失效特性。

针对维护条件下产品，从性能变化角度出发，定性分析了其可靠性规律，建立了可靠性模型，并进行了数值分析，验证了模型的可行性。在此基础上，重点分析了维护条件下产品在线寿命分布规律和总体寿命分布规律，并通过数值计算解释了失效特性。最后，以水泵转子为例，进一步验证了可靠性模型的可行性，并从寿命分布规律角度，说明了其集中失效的特性。

1 维护条件下产品性能变化描述及可靠性分析

1.1 产品性能变化描述

维护是产品最为常见的一种维修活动，如机械齿轮润滑、加油，机械齿轮调校等。在对机械齿轮进行润滑时，一般将润滑油涂抹到规定厚度，在船用仪表调校时，会通过机械标校等手段将指针重新归于零点等，其性能退化过程如图1所示。由此可见，维护活动会影响产品性能退化进程，且部分维护活动将产品的性能退化量恢复到规定值（通常记为零值）。本文将针对恢复性能退化量到规定值的维护活动，建立该条件下产品的性能可靠性模型，并分析其寿命分布规律。

如图1所示，产品性能退化量X（t）会在维护时刻ti（i∈N+）被恢复到零值，随后继续工作。由于有维护活动参与，导致产品性能退化过程具有两个特点：一是间断性，性能退化量因为维护而得到恢复，其在维护时刻出现间断点；二是突变性，随着维护次数的增加，每次维护后产品的性能退化量增幅越来越大，变化越来越急剧。

1.2 可靠性规律定性分析

维护会改变产品性能退化过程，进而影响其可靠性规律。由于性能退化量被恢复到零值，推迟了性能退化量到达失效阈值的时刻，因此，延长了产品的寿命。同时，性能退化量的急剧变化又导致产品在某个时刻可靠度会迅速下降，即失效概率大大增加。由此可见，为了开展维护条件下产品可靠性规律研究，需要重点考虑上述变化特性。

2 维护条件下产品性能可靠性模型

2.1 基本假设

随着产品性能退化过程认识的深入，部分产品的失效过程能够利用累积失效理论进行解释。累积失效理论将温度、湿度和振动等影响产品性能退化的各种客观因素统一为外界作用，外界作用会造成产品自身性能发生微小变化。随着时间的推移，微小变化量逐渐累积，当超过失效阈值时，便发生失效。

根据累积失效理论，对外界作用规律和作用引起的性能变化规律进行假设，具体如下：

1）假设外界作用规律服从强度函数为abtb-1的非齐次Poisson过程，即产品在工作时间内受到的外界作用次数满足式（1）：

2）每次外界作用将造成产品性能状态产生微小变化，工程中一般利用正态分布来描述其变化规律［15］。因此，设外界每次作用引起的性能变化量互相独立且服从相同的正态分布，即产品受到第i次作用引起的性能变化量Yi满足式（2）：

3）随机变量Ns，s+t和Yi分别与产品所处使用环境以及自身工艺水平有关，可以近似认为二者互相独立。

2.2 性能可靠性建模

根据复合Poisson过程的性质［16］，容易得到性能退化量的数学期望E（）和方差D（），具体表达式分别满足：

为了直观准确地描述产品性能退化量的变化规律，根据正态分布可加性，性能退化量仍服从正态分布，即：

其中，Φ（·）为标准正态分布的分布函数。

结合上述分析，得到维护条件下产品不同维护周期内性能退化量数值变化规律满足式（7）：

由式（7）和式（8）可知，产品性能退化量数值变化规律不仅与工作时间t有关，而且还与维护时刻密切相关，表现为参数和为工作时间和维护时刻的函数。

对于维护条件下产品，在掌握其各维护周期内性能退化量的数值变化规律（7）后，已知失效阈值Ls，则其在任意工作时间的可靠度 R（t）等价于前k-1个维护周期内性能退化量均未超过Ls，并且在时间内也没有超过Ls，具体表达式如下：

2.3 数值计算

利用数值仿真分析，对维护条件下产品的可靠度规律进行直观说明。设某产品受到外界作用次数N（t）服从强度函数为t0.5的非齐次Poisson过程，每次作用引起产品的性能变化量。假设每隔15天对产品进行周期性维护，且失效阈值Ls=0.5。

①可靠度函数计算。将上述参数代入到式（9）中，化简得到该产品可靠度函数满足式（11）：

从图2可以看出，对于维护活动参与的产品可靠性具有如下两个特点：

a.产品早期可靠度近似为1。因为维护延缓了性能退化量到达失效阈值的时间，推迟了产品的失效时刻，使其早期发生失效的概率极低，具有极高的可靠度。

b.每次维护后产品的可靠度呈现出阶梯状变化，即在近似保持平稳一段时间后快速下降。因为每次维护使产品的性能退化量恢复到零值，一段时间内性能退化量从零值到达失效阈值的概率极低（符合人们的直观认识），使产品维护后一段时间内的可靠度近似保持平稳。同时，图2中产品可靠度整体变化规律表明维护仅是降低了可靠度下降速度，并没有提高产品自身的可靠度水平。

为方便对比，图3中给出了不进行任何维修活动的产品可靠度曲线（图中虚线）。

图3中实线表示维护条件下产品的可靠度变化规律。没有维修活动参与条件下产品的可靠度下降较快，如其0.9可靠寿命仅为37.11 d，平均寿命仅为39.74 d；有维护活动参与条件下产品的0.9可靠寿命为118.49 d，平均寿命为133.15 d。由此可见，维护活动能够有效延长产品工作时间，对使用过程有着积极的影响，符合产品性能退化过程表现出来的特性。

②寿命特征计算。进一步计算，获得维护条件下产品寿命分布的概率密度函数，如图4所示。

由图4可知，在使用初期，产品寿命分布的概率密度函数数值极小，近似为零。随着使用时间的延长，概率密度函数数值逐渐增大，并呈现出集中的变化现象，表现为图4中数值变化集中于［105，150］时间区间内，说明在该时间区间内发生失效概率较高。上述变化与图2所示的性能变化规律较为吻合，进一步说明维护条件下产品具有早期可靠性高和集中失效的特性。

在工程中，使用方往往关心产品可靠度下降到一定程度时所对应的时间，即可靠寿命。对图2的数据进行整理，获得可靠寿命，部分数值如表1所示。

表1 产品可靠寿命数值表

由表1可知，产品可靠度由0.90下降到0.80，下降幅度较大，而其可靠寿命数值变化却十分小，仅由118.49 d变化为119.37 d。该现象说明维护条件下产品可靠度存在一个“拐点”。工程中表现为工作到该时刻后，同一批次的产品失效数量会迅速增多，出现集中失效。

3 维护条件下产品在线寿命分布规律

3.1 贴近度指标分析

上节建立的维护条件下产品性能可靠性模型实际上是针对同一批次的产品，属于在线（或个体）可靠性问题。通过上文可靠度规律分析，说明维护条件下产品具有集中失效的特性，与工程中常用的正态分布函数特性较为相似。因此，本节重点分析维护条件下产品在线寿命分布与正态分布的贴近性。

选取维护条件下产品在线寿命分布的偏度系数和峰度系数，分析维护条件下产品在线寿命分布与正态分布的贴近性。利用式（9），计算在线寿命分布的k阶原点矩uk，表达式如下：

利用式（12）和式（13），得到在线寿命分布的偏度系数β1和峰度系数β2，表达式如下：

通过分析偏度系数β1和峰度系数β2的数值，可以检验维护条件下产品在线寿命分布与正态分布的接近程度。如果偏度系数β1和峰度系数β2均接近于零值，说明维护条件下产品在线寿命分布形状与正态分布较为近似。

进一步，为了更好地说明维护条件下产品在线寿命分布与正态分布的贴近程度，计算偏差ε（t），表达式为：

3.2 数值计算

通过大量数值分析，计算维护条件下产品在线寿命分布的偏度系数、峰度系数和偏差值，以便进一步掌握其寿命分布特征。

对于不同批次的产品，使用环境的差异会使式（9）中的相关参数发生变化，导致个体之间的可靠性规律表现出一定差异性。随着工作时间的增加，个体差异性会越来越明显，出现喇叭口状［14］。由于篇幅有限，仅列出部分数值计算结果。在固定维护周期为80天的情况下，依据工程经验给定3组不同的模型参数，具体数值如表2所示。

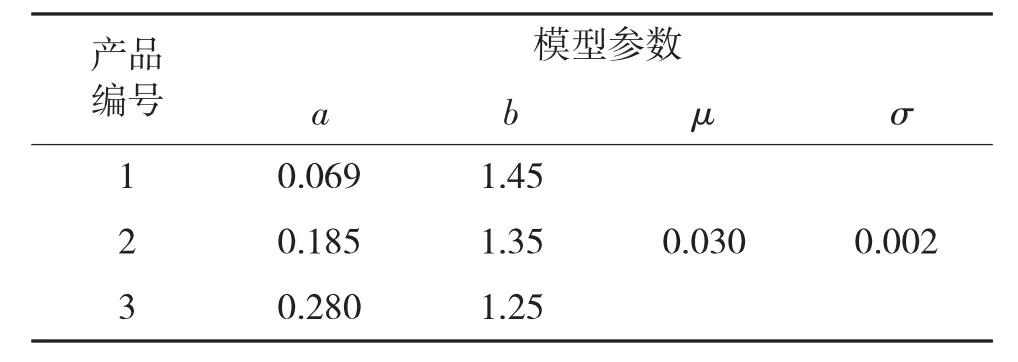
表2 模型参数数值表

针对表2中的模型参数，如果已知失效阈值Ls=6，对3台产品的寿命分布特征进行分析，具体步骤如下：

1）计算维护条件下产品在线寿命分布的概率密度函数。分别计算3台产品在线寿命分布的概率密度函数，具体如图 5 所示，图 5 中（a）～（c）分别对应3台产品：

由图5所示，概率密度函数的形状近似为拖尾的正态分布。同时，可以发现因为模型参数不同，3台产品的寿命分布规律有着明显的不同，即表现出差异性。

2）计算维护条件下产品在线寿命分布的偏度系数和峰度系数。利用式（14）分别计算3台产品寿命分布的偏度系数和峰度系数，具体数值见表3所示。

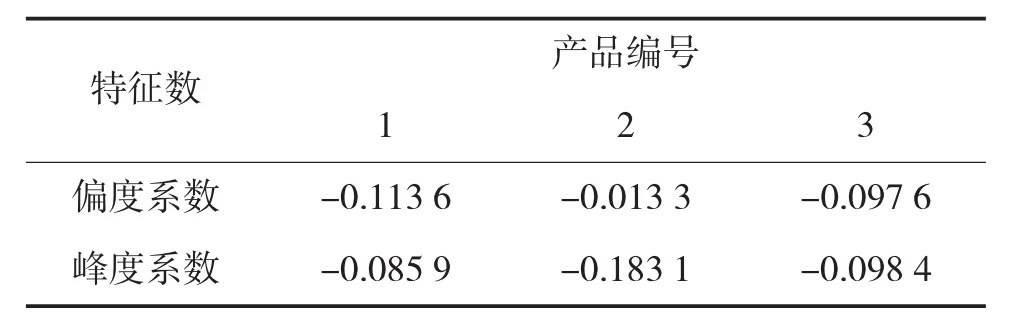
表3 偏度系数和峰度系数数值表

由表3可知，3台产品的偏度系数和峰度系数均接近零值，可见其形状特征与标准正态分布较为一致。

3）计算近似维护条件下产品在线寿命分布的正态分布。针对3台产品，利用式（12）确定正态分布的相关参数，具体数值见下页表4所示。

表4 正态分布参数数值表

4）计算正态分布近似维护条件下产品在线寿命分布的偏差。针对3台产品，已知正态分布参数如表4所示，利用式（15）对近似产生的偏差进行计算，分别获得3台产品的最大偏差值εmax和对应时刻tmax。如上节所述，维护条件下产品具有早期可靠性较高的特性。对于该类产品，使用方往往关心其在高可靠度条件下的分布规律，对于实际意义并不重要的低可靠度条件下的分布规律并不关心。因此，计算得到在高可靠度条件下（指R（t）＞0.8）的最大偏差值和对应时刻。具体数值见表5所示：

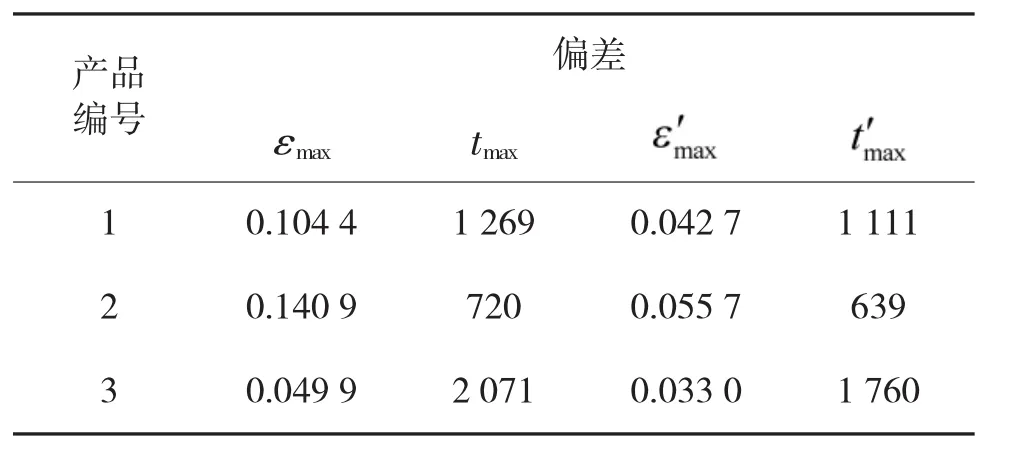
表5 偏差数值表

如表5可知，利用正态分布近似产品在线寿命分布产生的偏差较小。特别是在高可靠度的条件下，正态分布能够较好地近似产品在线寿命分布，精度较高。由此可见，维护条件下产品在线寿命分布与正态分布具有较好的贴近性，进一步说明了其集中失效的特性。

4 维护条件下产品总体寿命分布规律分析

4.1 总体寿命分布建模

由3.1节分析可知，维护条件下产品个体之间的寿命分布规律存在一定的差异性，造成差异的重要原因是不同产品受到的外界作用规律不一致。具体到性能可靠性式（9），外界作用规律不一致主要表现为相关参数a和b的取值不同。因此，不同批次的产品所处使用环境往往不同，造成性能参数a和b的数值有所不同，可近似认为a和b在某个区间进行均匀波动，即分别服从均匀分布，表达式为：

在掌握性能参数a和b的变化规律后，利用性能可靠性式（9），得到产品的总体寿命分布F总（t）：

4.2 贴近度指标分析

实际中，通过收集整理不同批次或者个体的失效数据，能够发现产品总体的寿命分布规律与个体的寿命分布规律存在明显不同。从失效规律来看，产品总体失效具有一定的随机性，并不具有产品个体集中失效特点。随着技术的发展，产品的复杂程度越来越高，包含了大量的机械和电子元器件，属于机电一体设备，而工程经验表明该类产品的寿命分布往往服从指数分布［17］。比如，以平台式惯性导航系统为例，对于同一批次或者单个系统，其失效往往具有集中性，但是对于多批次系统，其失效往往具有随机性，寿命分布近似为指数分布。因此，本节重点分析产品总体寿命分布与指数分布的贴近性。

记维护条件下产品总体可靠度为R总（t），满足。如果已知维护时刻，利用最小二乘法拟合得到指数分布参数λ。具体步骤如下：

其中 n＜e。

4.3 数值计算

通过大量数值计算，对指数分布近似维护条件下产品总体寿命分布产生的偏差进行分析，限于篇幅有限，仅罗列部分数值计算结果。

结合维护条件下产品总体寿命分布规律（17），给定相关性能参数：假设产品受到外界作用次数服从强度函数为abtb-1的非齐次Poisson过程，其中每次作用后引起产品的性能变化量Yi服从正态分布。固定维护周期为180天，已知失效阈值Ls=6，利用式（17）得到产品总体寿命分布函数：

利用式（19），拟合得到指数分布的分布函数，并与产品总体寿命分布函数进行对比，如图6所示。

图中实线为指数分布的分布函数。由图6可知，维护条件下产品总体寿命分布与指数分布有着较好的贴近性，且利用指数分布近似总体寿命分布具有一定的保守性。

进一步分析，利用式（18）对利用指数分布近似总体寿命分布产生的偏差进行计算，限于篇幅，对部分工作时刻的真实值、近似值和偏差进行罗列，具体数值如表6所示。

由表6可知，利用指数分布近似维护条件下产品总体寿命分布产生的偏差较小，精度较高，具有较好的贴近性。因此，可以认为维护条件下产品总体寿命分布近似服从指数分布，较好解释了工程中产品总体失效往往具有随机性的特性。

表6 分布函数值比较表

5 工程算例

某水泵转子在使用过程中会定期进行润滑保养。根据要求，涂抹润滑油的厚度每次为固定值，因此，可以近似认为水泵转子在使用过程中定期润滑（即维护）能够将其状态恢复到零值。通过整理实际工程中的失效数据，能够得到某组水泵转子的失效规律曲线如图7所示。

如图7所示，在工作初期（前10个周期内），转子失效数据极少，仅为1个。随着时间的延长，在第12个～14个周期，失效数据迅速增加，由2个增加到40个。由此可见，该组水泵转子具有早期可靠性极高和集中失效的特点。磨损失效的相关理论［18］可以较好地解释该现象：产品使用过程会经历正常磨损阶段，该阶段磨损率较为稳定，不易发生失效。随后会经历严重磨损阶段，此时，产品较容易发生失效。

针对图7中水泵转子的失效特征，利用本文的方法进行处理，在已知失效阈值Ls=0.04和维护周期Δt=10天的情况下，获得水泵转子相关参数值：受到外界作用次数N（t）服从强度函数为0.21t0.75的非齐次Poisson过程，每次作用对性能退化量造成的变化量。综上，利用式（9）化简得到水泵转子的可靠度函数满足式（20）：

由图8可知，水泵转子早期可靠度极高，近似为1。随着使用时间的延长，可靠度逐渐降低，特别是在时间区间［120，140］内，可靠度由0.95迅速下降到0.60。可见，可靠度存在一个“拐点”，使其变化较为剧烈，出现集中失效。由此可见，本文方法较好地描述了水泵转子早期可靠度极高和集中失效的特性。

进一步分析，利用本文方法得到的水泵转子失效规律与其实际失效数据表现出来的规律进行对比，具体效果如图9所示。

图9中实线为实际值，表示水泵转子失效数据表现出的失效规律；虚线为解析值，表示利用本章方法得到的失效规律。如图9所示，解析值与实际值的变化曲线较为接近，可见本文方法能够较好地描述水泵转子的失效规律。

在掌握水泵转子维护条件下可靠性规律的基础上，利用本文方法分析其寿命分布规律。已知水泵转子可靠度规律，计算该组水泵转子寿命分布的偏度系数和峰度系数，分别为-0.128 3和-0.081 7，可见其与零值较为接近，说明其分布形状与正态分布较为接近。利用正态分布近似水泵转子寿命分布，并计算二者的偏差，获得最大偏差值εmax和对应的时刻tmax。并进一步计算，获得高可靠度条件下（R（t）≥0.8）产品的最大偏差值和对应的时刻具体数值如表7所示。

表7 水泵转子偏差数值表

如表7可知，利用正态分布近似水泵转子寿命分布产生的偏差较小。特别是在高可靠度的条件下，利用正态分布近似效果较好。

6 结论

针对维护条件下产品，建立了性能可靠性模型，并重点对其在线寿命分布规律和总体寿命分布规律进行了研究。通过开展数值分析和工程计算，取得了以下结论：

1）从维护条件下产品性能变化特点，结合累积失效理论，建立了该条件下产品的性能可靠性模型，较好地描述了其可靠度规律，并反映了其早期可靠性高和集中失效的特点；

2）结合维护条件下同一批次产品失效特点，利用偏度-峰度分析和偏差分析，对该条件下产品在线寿命分布与正态分布的贴近性进行了研究，说明了二者具有较好的贴近性，从寿命分布角度解释了工程中同一批次产品失效往往具有集中性的特点，进一步掌握了维护条件下产品在线寿命分布规律，为延寿、寿命预测等研究奠定了一定的理论基础。

3）在上述研究基础上，建立维护条件下产品总体寿命分布模型，利用偏差分析对其与指数分布的贴近性进行了研究，说明了二者具有较好的贴近性，从寿命分布角度解释了工程中产品总体失效往往具有随机性的特点，进一步掌握了维护条件下产品总体寿命分布规律。

［1］中国人民解放军总装备部.GJB451A-2005可靠性维修性保障性术语［S］.北京：中国人民解放军总装备部，2005.

［2］LI D W，ZHANG Z H，ZHONG Q H，et al.Performance deterioration modeling and optimal preventive maintenance strategy under scheduled servicing subject to mission time［J］.Chinese Journal of Aeronautics，2014，27（4）：821-828.

［3］SILVA J E，GARBATOV Y，SOARES C G.Reliability Assessment of a steel plate subjected to distributed and localized corrosion wastage［J］.Engineering Structures，2014，59（2）：13-20.

［4］刘强.基于失效物理的性能可靠性技术及应用研究［D］.长沙：国防科学技术大学，2011.

［5］WILSON S P，TAYLOR D.Reliability assessment from fatigue micro-crack data ［J］.IEEE Transactions on Reliability，1997，46（2）：165-172.

［6］GONZALEZ D S，ALJO R J R，CANTU M，et al.A non-linear fuzzy regression for estimating reliability in a degradation process［J］.Applied Soft Computing，2014，16：137-147.

［7］GUIDA M，PULCINI G.The inverse gamma process：a family of continuous stochastic models for describing state-dependentdeterioration phenomena ［J］.Reliability Engineering&System Safety，2013，120：72-79.

［8］谭林，程志君，郭波.考虑不完全维修的可修串联系统可用度模型［J］.国防科技大学学报，2009，31（6）：100-105.

［9］赵建印，刘芳，孙权，等.基于性能退化数据的金属化膜电容器可靠性评估［J］.电子学报，2005，33（2）：378-381.

［10］任淑红，左洪福，白芳.基于带漂移的布朗运动的民用航空发动机实时性能可靠性预测［J］.航空动力学报，2009，24（12）：2796-2801.

［11］JIAN W C，KIM H L，LAM Y.Bayesian computation for geometric process in maintenance problems ［J］.Mathematics&Computers in Simulation，2010，81（4）：771-781.

［12］WANG X L，JIANG P，GUO B，et al.Real-time reliability evaluation based on damaged measurement degradation data［J］.Journal of Central South University，2012，19（11）：3162-3169.

［13］彭宝华.基于Wiener过程的可靠性建模方法研究［D］.长沙：国防科学技术大学，2010.

［14］OLIVEIRA M D D，COLOSIM E A，GILARDONI G L.Bayesian inference for power law processes with applications in repairable systems［J］.Journal of Statistical Planning&Inference，2012，142（5）：1151-1160.

［15］彭宝华，周经伦，金光.综合多种信息的金属化膜电容器可靠性评估［J］.强激光与粒子束，2009，21（8）：1271-1275.

［16］樊平毅.应用随机过程［M］.北京：清华大学出版社，2006.

［17］张志华.可靠性理论及工程应用［M］.北京：科学出版社，2012.

［18］ARTANA K B，ISHIDA K.Spreadsheet modeling of optimal maintenance schedule for components in wear-out phase［J］.Reliability Engineering&System Safety，2002，77（1）：81-91.

Analysis of Life Distribution Rule for Product on Servicing

LI Da-wei，FANG Yong，SUN Xing
（Unit 91550 of PLA，Dalian 116023，China）

Considering the characteristics of performance deterioration，the reliability model is established from the cumulating failure mechanism by compound Poisson process.So it can get the life distribution rule for product on servicing and explain the failure characteristics.The on-line life distribution model is also built.On the basis of it，the collectivity life distribution model is developed.Through the number analysis of skewness-kurtosis and nearness，the on-line life distribution of product on servicing is approximately normal distribution，and the collectivity life distribution of product on servicing is approximatelyexponential distribution.So it explains the characteristics of centralized-failure and random-failure.Finally，it can describe the reliability and life distribution of water rotor on scheduled servicing byabove models.The applicability and accuracyof models are shown.

life distribution，servicing，performance reliability model，compound poisson process

TH17

A

10.3969/j.issn.1002-0640.2017.11.16

1002-0640（2017）11-0068-09

2016-09-23

2016-11-25

李大伟（1985- ），男，山东威海人，博士，工程师。研究方向：性能退化建模与评估，可靠性试验等。