高地隙自走式喷雾机发动机悬置系统优化设计

郑继周，黄 瑞，吴彦强，侯加林

(1.山东农业大学 机械与电子工程学院，山东 泰安 271018； 2.山东省园艺机械与装备重点实验室，山东 泰安 271018)



高地隙自走式喷雾机发动机悬置系统优化设计

郑继周1,2，黄 瑞1,2，吴彦强1,2，侯加林1,2

(1.山东农业大学 机械与电子工程学院，山东 泰安 271018； 2.山东省园艺机械与装备重点实验室，山东 泰安 271018)

某经济型高地隙自走式喷雾机使用三缸发动机作为动力，但低速作业时整车振动剧烈，对喷雾性能产生了不利影响。针对这一问题，对悬置系统进行重新设计。低速运行时，激励主要来自绕曲轴轴线的转矩波动，故采用隔振器斜置式布置方案。根据振动理论，对隔振器安装位置和倾斜角度进行计算和优化。理论分析和试验结果表明:改进设计后,整车振动情况得到较大改善。

高地隙自走式喷雾机；发动机悬置系统；减振

0 引言

随着能源危机和环境污染的不断加剧，小排量发动机的应用越来越广泛，同时对其性能要求也越来越高。作为小型发动机中的一种，三缸汽油机具有升功率高及结构紧凑等优点，已大量应用于小型汽车及农用机械等领域。然而，三缸汽油机固有的平衡性差问题会引起整机振动，产生不利的影响。因此，需要合理设计发动机悬置系统以实现隔振[1-4]。目前，多采用优化方法对悬置系统的刚度参数进行优化，匹配合理的悬置系统刚度，以减小发动机传递到支承系统的振动[5-8]。

某单位自主开发了一款高地隙自走式喷雾机，其动力采用一台三缸汽油机。样机试验过程中发现低速工作时发动机振动剧烈，严重影响了整机舒适性、可靠性和喷雾性能。为此，从隔振理论出发，结合理论分析和试验验证，对该发动机悬置系统进行优化设计，取得了较好效果。

1 基本理论

发动机悬置系统一般采用“刚体-弹性支承”模型[9-10]，即发动机视为空间自由刚体，通过3～4个弹性元件支承在刚性机架上。这样，系统具有6个自由度，即纵向、横向、垂向、纵摇、横摇、平摇。设计发动机悬置系统时，应尽可能解除这6个自由度之间的振动耦合，即解耦[11-13]。解耦的好处有两个：一方面便于减小可能激起共振响应的频带宽度；另一方面便于合理配置固有频率，使激励频率远离共振频率，获得良好的整体隔振效果。

解耦设计包括惯性解耦、激励解耦和弹性解耦。大量实例表明：发动机在曲轴坐标系下的惯性积一般都较小，远小于其转动惯量，因此惯性耦合较弱。同时，发动机低速时的激励主要为绕曲轴轴线的转矩波动，高速时的激励主要来自于不平衡惯性力，沿气缸轴线方向，因此激励之间不存在耦合。这样仅需要考虑弹性解耦。采用斜置式布局(隔振器对称倾斜放置成V形)可以比较容易地实现弹性解耦。建立发动机的曲轴坐标系，如图1所示。

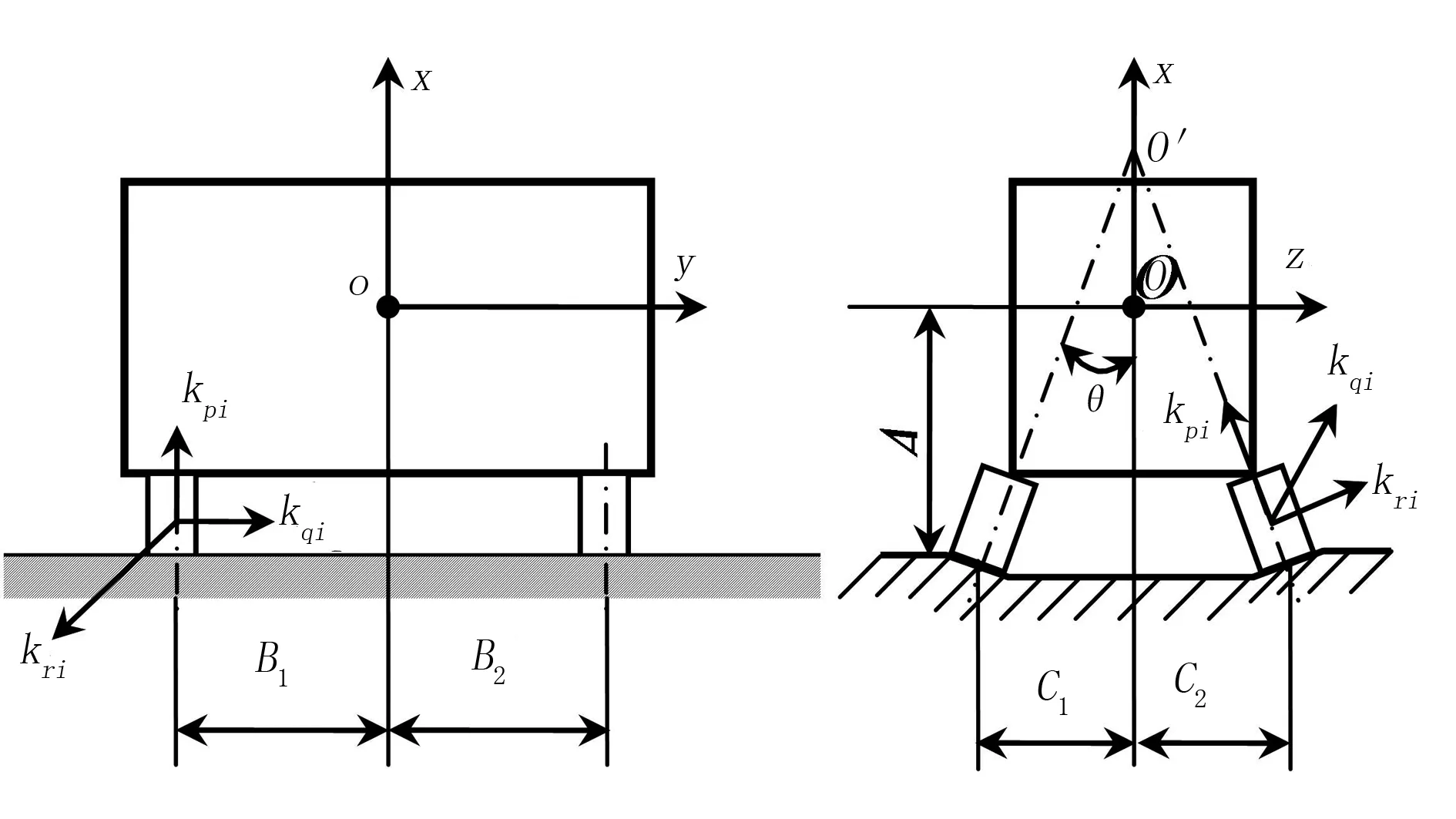
图1 斜置式悬置系统示意图

图1中，坐标原点O位于发动机的质心；x轴平行于气缸中心线，指向发动机缸盖；y轴平行于曲轴中心线，指向发动机前端；z轴按正交坐标系的左手定则确定。在此坐标系下，发动机的转矩波动激励作用于绕y轴方向，不平衡惯性力激励作用于x轴方向，激励之间不存在耦合。此时系统的6个自由度分别为：纵向(沿y轴)、横向(沿z轴)、垂向(沿x轴)、纵摇(绕z轴旋转)、横摇(绕y轴旋转)、平摇(绕x轴旋转)。

隔振器的安装应力求规则布置，这不但对振动控制有利，而且也便于安装实施[14-15]。在斜置式布局中，同样也要遵循这一原则。此处采用4个相同的隔振器，并使隔振器相对于xoy、xoz平面对称布置，即B1=B2、C1=C2。同时，隔振器的两个弹性主轴p、r分别与xoy、yoz平面倾斜相同的角度θ，第3个弹性主轴q沿y轴方向。

对于图1所示的隔振器布置方式，其弹性主轴p与x、y、z轴之间的夹角分别为θ、π/2、π/2±θ；弹性主轴q与x、y、z轴之间的夹角分别为π/2、0、π/2；弹性主轴r与x、y、z轴之间的夹角分别为π/2±θ、π/2、θ。此时，系统的刚度计算公式可简化为[14-15]

KXX=n(kpcos2θ+krsin2θ)

KYY=nkq

KZZ=n(kpsin2θ+krcos2θ)

2n(kp-kr)sinθ·cosθ·A·C

KYγ=-nkqA

KZβ=n(kpsin2θ+krcos2θ)A-

n(kp-kr)sinθ·cosθ·C

式中 KXX、KYY、KZZ—系统沿x、y、z轴的平移刚度；

Kαα、Kββ、Kγγ—系统绕x、y、z轴的回转刚度；

KYγ—系统纵向与纵摇之间的耦合刚度；

KZβ—系统横向与横摇之间的耦合刚度；

kp、kq、kr—隔振器沿3个弹性主轴的刚度；

Ai、Bi、Ci—隔振器的布置位置；

N—隔振器的个数。

可见，悬置系统的刚度与以下因素有关：隔振器的个数、各隔振器的安装位置、各隔振器的弹性主轴与曲轴坐标系之间的角度及各隔振器沿弹性主轴方向的刚度。

当KZβ=0时，可以实现横向与横摇的解耦，即

(kpsin2θ+krcos2θ)A=(kp-kr)sinθ·cosθ·C

从上式可以导出

其中，R=A/C为高宽比；K=kp/kr为隔振器压缩与剪切刚度之比。

当隔振器的布置尺寸A/C满足上式时，即可做到横向、横摇的独立。针对不同的K，根据上式可以绘制出R与θ的关系，如图2所示。已知R、θ、K三者中的任意两个，就可按该图确定另外一个。

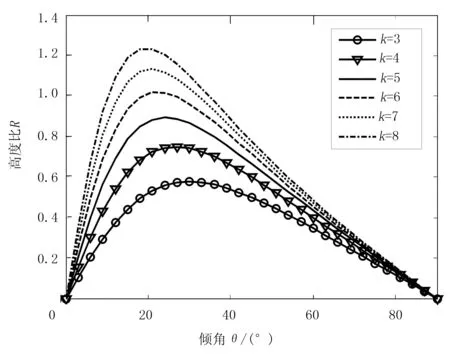
图2 隔振器刚度、安装角度和安装位置的关系

2 悬置系统优化设计

根据振动理论，当系统的固有频率和相应的激励频率相同时，整个系统将发生共振，振动幅值大大增加。因此，解耦并不是最终目的，将系统解耦后的各阶固有频率控制在预定范围内才是悬置系统设计的根本。

对于“刚体-弹性支承”系统，固有频率取决于悬置系统的刚度和发动机的物理属性(质量、惯性积和转动惯量等)。其中，发动机一旦选定，其物理特性基本无法改变。因此，悬置系统设计主要通过改变悬置系统的刚度来实现。

2.1 优化目标函数

对于3缸发动机，低频范围内其主要扰动力为绕曲轴轴线的转矩波动。当此激励频率和横摇固有频率重合时，系统发生共振。高频范围内的主要扰动力为不平衡惯性力。当此激励频率与垂向固有频率相同时，系统也会发生共振。因此，发动机的隔振设计对垂向和横摇固有频率及解耦有较高要求，其它4个固有频率只要控制在一定范围内即可。因此，优化目标函数可以写成如下形式

式中x—设计变量；

f0(z)、f0(β)—设计要求的固有频率值；

f(z)、f(β)—悬挂系统的实际频率值；

dig—解耦性(完全解耦时等于1)；

W1、W2、W3、W4—加权系数。

2.2 设计变量

如前所述，系统的刚度与隔振器的个数、刚度、安装位置和倾斜角度有关。其中，调整隔振器的位置对刚度及系统的解耦影响最大，收效也最明显。因此，本文以隔振器的安装位置和倾斜角度为设计变量，进行悬置系统优化设计。

2.3 约束条件

发动机的激励频率计算公式为

式中f—激励频率(Hz)；

n—发动机转速(r/min)；

i—发动机缸数；

τ—发动机冲程数。

该发动机为3缸4冲程汽油机，怠速转速为950r/min，因此激励频率为23.75Hz。

当发动机在较高转速范围内运行时，转矩波动不再处于主导地位，垂向的往复惯性力成为主要的激励来源。因此，垂向固有频率可以取得比横摇固有频率大一些，其取值范围设为15Hz≤f0(z)≤20Hz。

该喷雾机整体设计已经基本定型，各种覆盖件和药箱都由相应的模具加工完成。因此，悬置系统优化设计只能在发动机和现有车架之间的有限空间内进行。考虑隔振器本身以及相应支座的尺寸，高度、长度和宽度方向的可用空间分别为：120mm≤A≤140mm、70mm≤B≤100mm、130mm≤C≤190mm。

隔振器采用橡胶隔振器，其压缩刚度大于剪切刚度(二者之比一般介于3～8之间)。基于这一特性，隔振器倾斜角度的取值范围设定为0°≤θ≤50°。

2.4 优化设计方法

在优化目标函数中既包括固有频率的配置又有解耦性要求，是一个有约束的优化问题。由于仅含有不等式约束，此处采用随机方向法求解。

2.5 系统参数及设计变量优化

发动机的质量m，绕x、y、z轴的转动惯量Ix、Iy、Iz如表1所示。惯性积较小，忽略不计。

表1 发动机的物理属性

弹性支承采用橡胶隔振器，压缩刚度约为40 000N/m，剪切刚度约为80 000N/m。

优化前，隔振器布置主要考虑的是布局方便，采用了前斜置后平置的方式。其中，前悬置两个隔振器的倾斜角度均为45°。各悬置点相对于质心的位置如表2所示。

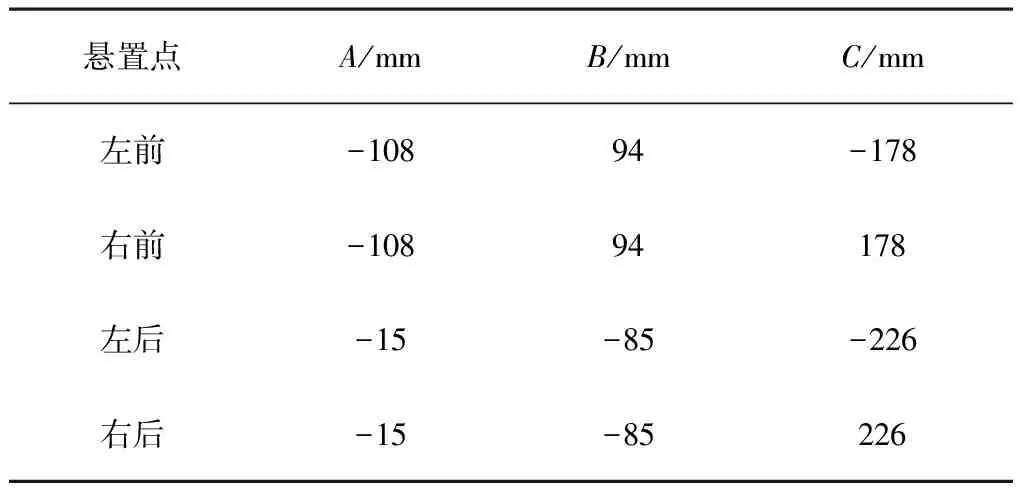
表2 优化前各悬置点的位置

可以看出：在原有设计中虽然考虑了左右对称，但前后和垂向的尺寸并不对称，从而导致了系统6个自由度之间的相互耦合。这一点从后文中的图3可以直观地看出。

优化后的悬置系统采用了4个相同的隔振器，而且左右、前后均对称布置。利用优化设计方法，并结合图2(隔振器刚度、安装角度和安装位置的关系)，最终确定高度A=130mm，长度B=80mm，宽度C=150mm，倾角θ=30°。

3 模态分析与实验验证

利用上述各项参数，分别对优化前后发动机悬置系统进行模态分析，得到其6阶固有频率和相应振型，如图3、图4所示。

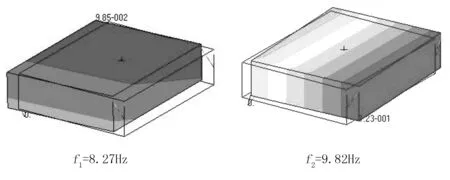
图3 优化前悬置系统各阶固有频率和振型

图4 优化后悬置系统各阶固有频率和振型

由图3可以看出：优化前悬置系统的设计没有实现解耦—只有第4阶模态(以平摇为主)解耦程度略高，其余各阶模态均存在较大程度的耦合。其中，第6阶模态以横摇为主，且固有频率为23Hz，正好接近发动机怠速时的激励频率23.75Hz。如前所述，此时发动机的激励主要为绕曲轴轴线的转矩波动。激励频率接近固有频率，且各阶模态均未实现解耦，整车产生剧烈振动也就在所难免了。

由图4可以看出：采用隔振器斜置式方案后，实现了4个自由度的解耦，即垂向、平摇、横向及横摇，而纵向-纵摇仍然是耦合的。无疑，这对合理配置系统的各阶固有频率是有利的。

与平置式比较，斜置式布局使系统的横摇刚度减少、横向刚度增加。具体表现为：优化前，第2阶模态以横向为主，优化后则变成了第4阶模态，且固有频率有所增加；优化前，第6阶模态以横摇为主，优化后则成了第5阶模态，且固有频率明显降低。这一点正与发动机的激励特点对应，因此斜置式布局非常适合于发动机的隔振：一方面有利于隔离横摇方向的转矩波动激励，另一方面可以增强隔振装置的横向稳定性。同时，系统抵御外界倾斜、摇摆的能力也会有所增强。

优化后，不仅实现了横向和横摇的解耦，而且横摇的固有频率低于垂向的固有频率。怠速时，激励频率(23.75Hz)约为横摇固有频率的1.7倍。因此，悬置系统能够成功隔离转矩波动引起的横摇振动。

为了验证悬置优化后的隔振效果，进行了整车振动试验。左前悬置沿横向的振动传递率、左后悬置沿纵向的振动传递率分别如图5、图6 所示。

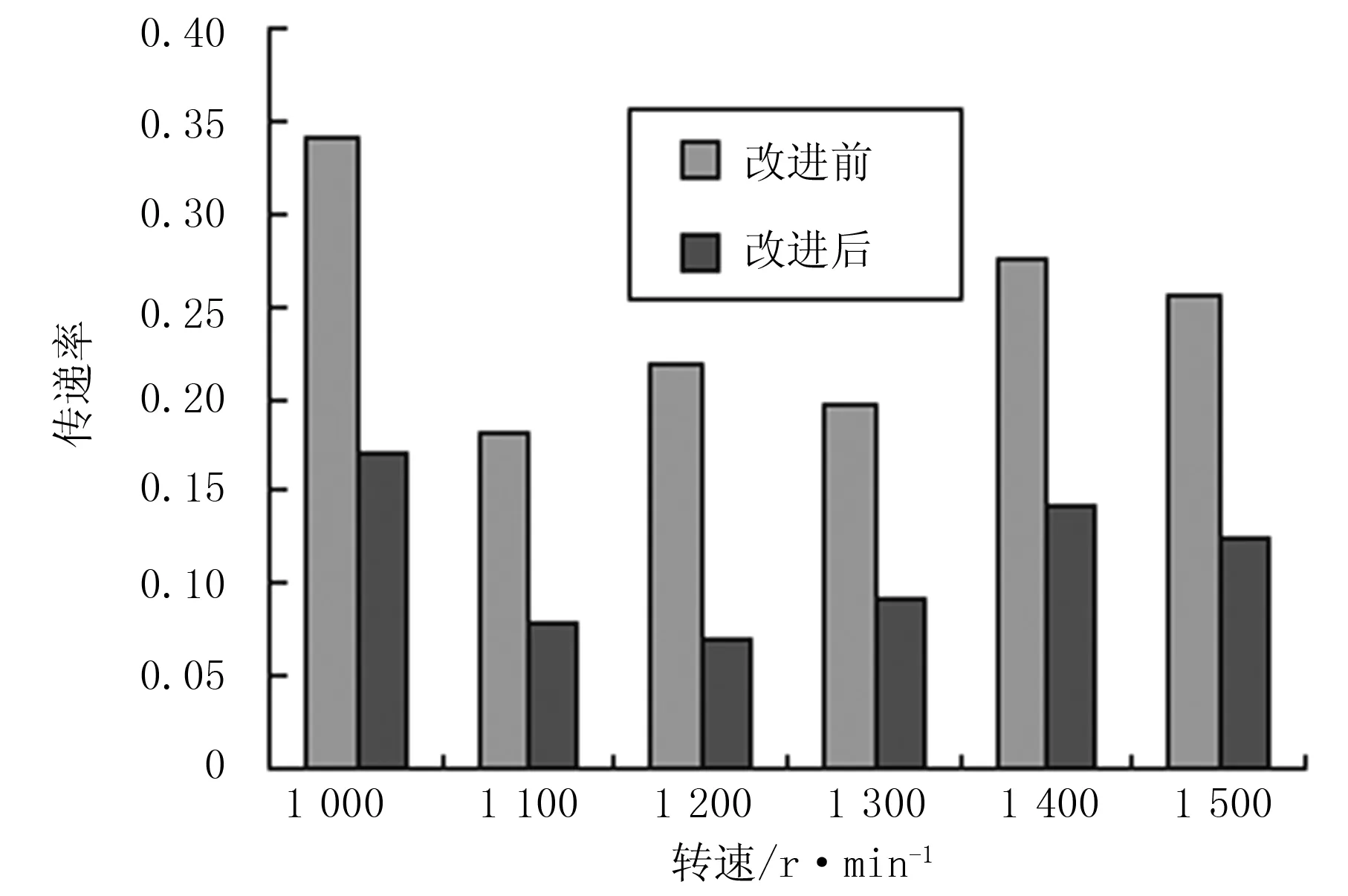
图5 左前悬置横向传递率

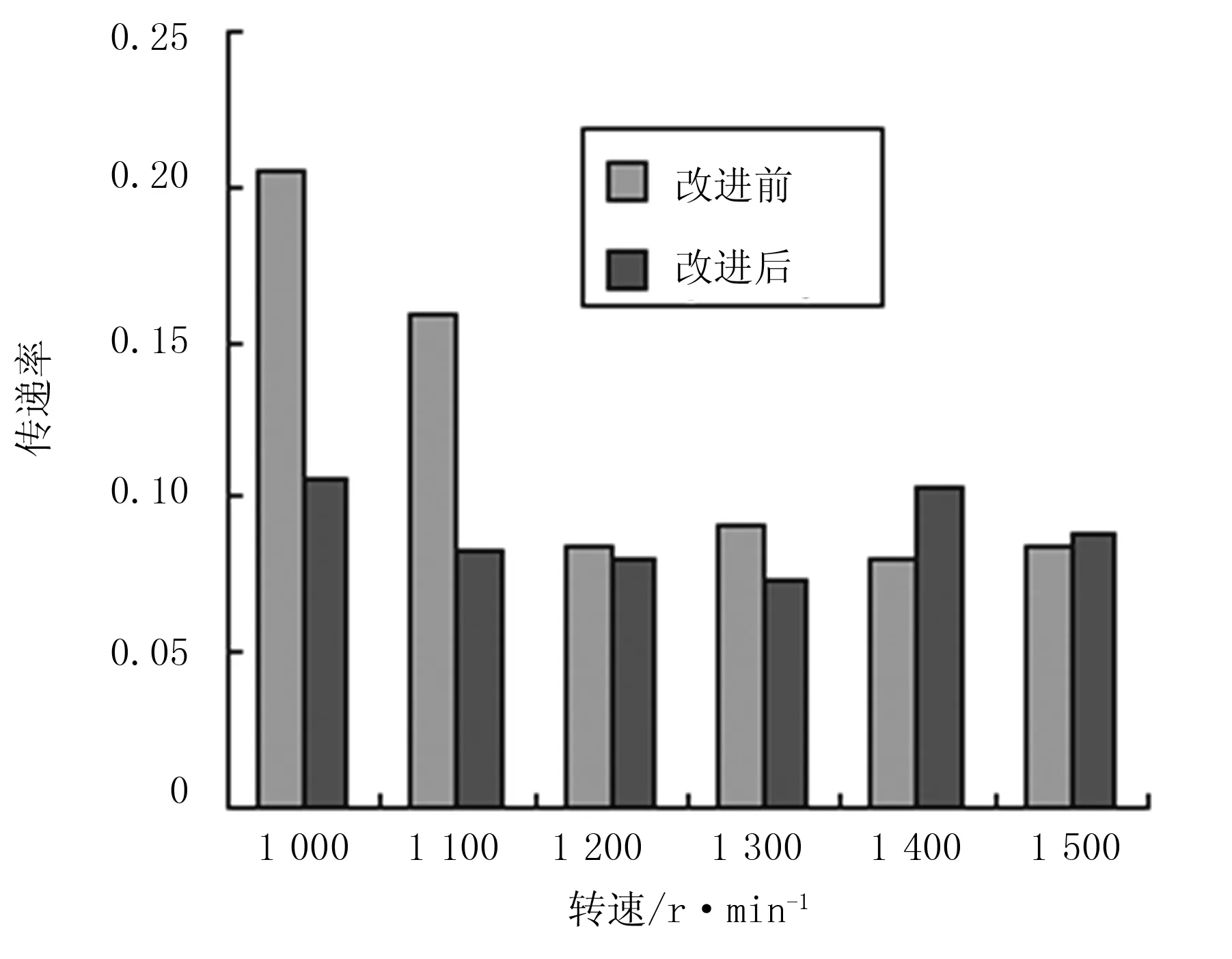
图6 左后悬置纵向传递率

由图5、图6可以看出：悬置优化设计后，整车振动状况得到了较大的改善，横摇振动明显低于改进前。特别是在怠速转速附近(1 000～1 300r/min)时，减振效果更加明显。虽然在1 400～1 500r/min范围内纵向传递率略有增大，但其振动本来就较小，几乎不会产生不利影响。

4 结论

针对高地隙自走式喷雾机整车振动问题，分析其动力源三缸发动机的振动特性，采用隔振器斜置式布局方案，对悬置系统进行优化设计。结合实际情况，合理选择弹性支承元件的刚度、安装位置和倾斜角度，实现了横向和横摇的解耦，并将横摇振动的固有频率控制在合理范围内。现场试验证明：该方案可有效降低整车低速时的振动。

[1] 庞剑, 谌刚, 何华. 汽车噪声与振动：理论与应用[M]. 北京: 北京理工大学出版社, 2006.

[2] 吕振华,范让林.动力总成-悬置系统振动解耦设计方法[J].机械工程学报,2005, 41(4):49-54.

[3] 范让林,吕振华.刚体-弹性支承系统振动解耦评价方法分析[J].工程力学,2006, 23(7):13-18.

[4] 童树波,夏长高.汽车动力总成液压悬置元件特性研究[J].农机化研究,2003(4):199-201.

[5] 陈克,李晓政,周霜霜.动力总成悬置系统优化与减振分析[J].沈阳工业大学学报,2016(1):57-62.

[6] 张武,陈剑,高煜.基于粒子群算法的发动机悬置系统稳健优化设计[J].农业机械学报,2010, 41(5):30-35．

[7] 周洪威,李雪梅,刘夫云,等.叉车振动仿真及发动机总成悬置优化[J].噪声与振动控制,2014(6):65-70，89.

[8] 谢展,于德介,李蓉,等.基于区间分析的发动机悬置系统稳健优化设计[J].汽车工程,2014(12):1503-1507，1527.

[9] 张玉增,柴山,刚宪约,等.发动机悬置系统的研究综述[J].农业装备与车辆工程,2012(1):23-27,30.

[10] 陈树勋,尹国保,黄锦成,等.基于等效分析模型的发动机悬置系统优化设计[J].工程力学,2013(11):221-226.

[11] 范让林,吕振华.刚体-弹性支承系统振动解耦评价方法分析[J].工程力学,2006(7):13-18.

[12] 陈大明,上官文斌.横置动力总成悬置系统的布置设计分析[J].新技术新工艺,2012(1):25-28.

[13] 陈剑,徐陈夏.发动机悬置系统优化设计及其可靠性分析[J]. 汽车工程,2009(3):234-238.

[14] 严济宽, 陈全福.弹性支承物体的固有频率(一) [J].中国造船,1980(4):107-116.

[15] 严济宽,陈全福.弹性支承物体的固有频率(二)[J].中国造船,1981(1):68-79.

Optimal Design of Engine Suspension System for High Clearance Self-propelled Sprayer

Zheng Jizhou1,2, Huang Rui1,2, Wu Yanqiang1,2, Hou Jialin1,2

(1.Mechanical and Electronic Engineering College, Shandong Agricultural University, Tai'an 271018, China; 2.Shandong Provincial Key Laboratory of Horticultural Machinery and Equipment, Tai'an 271018, China)

A three-cylinder engine is used for high clearance self-propelled sprayer for the reason of economy. However, violent vibration is observed when the sprayer works at a low velocity. It is necessary for the optimal design of the engine suspension system. The excitation is mainly fluctuation of torque around the crank axis of engine in this instance, so a scheme where the isolators are obliquely placed is adopted. The oblique angle and location of isolators are calculated and optimized according to vibration isolation theory. The results of test show that the vibration of sprayer has been reduced largely.

high clearance self-propelled sprayer; engine mounting system; vibration reduction

2016-01-31

山东省农机化装备研发创新项目(NJGG201501)；山东省现代农业产业技术体系创新团队项目(SDAIT-02-021-09)

郑继周(1977-)，男，山东阳谷人，副教授，(E-mail) jzzheng@sdau.edu.cn。

侯加林(1963-)，男，山东高密人，教授，博士生导师，(E-mail)jlhou@sdau.edu.cn。

S491

A

1003-188X(2017)02-0232-05