THPFSY-2型双容水箱液位实验系统鲁棒故障诊断

2017-12-15陈虹丽刘纹岩

实验室研究与探索 2017年11期

关键词：参考模型水箱液位

陈虹丽，李强，刘纹岩

(1. 哈尔滨工程大学自动化学院，哈尔滨 150001; 2. 上海卫星工程研究所，上海 201100)

·仪器设备研制与开发·

THPFSY-2型双容水箱液位实验系统鲁棒故障诊断

陈虹丽1，李强1，刘纹岩2

(1. 哈尔滨工程大学自动化学院，哈尔滨 150001; 2. 上海卫星工程研究所，上海 201100)

研究了THPFSY-2型双容水箱在干扰和故障作用下的鲁棒故障诊断问题。首先根据双容水箱机理模型建立双容水箱的T-S模糊模型，然后通过引入参考模型，建立有关故障残差估计误差的广义残差方程，将基于T-S模型的故障诊断滤波器设计问题转换成了典型的系统鲁棒控制问题。根据有界实引理给出了参数最优解的线性矩阵不等式解的形式，并对其正确性进行了证明。通过仿真验证了该算法在双容水箱故障诊断中的有效性。

双容水箱； T-S模型；鲁棒故障诊断；线性矩阵不等式

0 引言

双容水箱[1]是工业上常见的控制对象，可以模拟实际工业生产中多种常见的控制过程，因此很多大学过程控制实验室均配备了双容水箱实验系统，用于在实验室模拟实际的工业控制问题[2]，而故障诊断研究对保障水箱这类复杂非线性系统的可靠性与稳定性，具有重要意义[3]。

本文选择THPFSY-2型双容水箱实验系统作为故障诊断研究的对象，通过引入参考模型，建立起有关故障残差估计误差的广义残差方程，并对其正确性进行了验证，可以较好地实现在实验室模拟研究工业上常见故障的诊断与分析[4]，具备一定的实践意义。

1 THPFSY-2型双容水箱总体架构

双容水箱实验系统由水箱容器、水泵、电气控制箱、液位传感器及控制计算机组成，其总体结构示意图见图1，系统原理图如图2所示。水箱参数如下：水箱横截面积S=154 cm2，连通阀横截面积Sn=5 cm2,液位最大值Hmax=60 cm，重力加速度g=980 cm/s2，CV1流量系数az1=0.447 0，CV2流量系数az2=0.645 8，其具体值为实验所得。

(a)

(b)

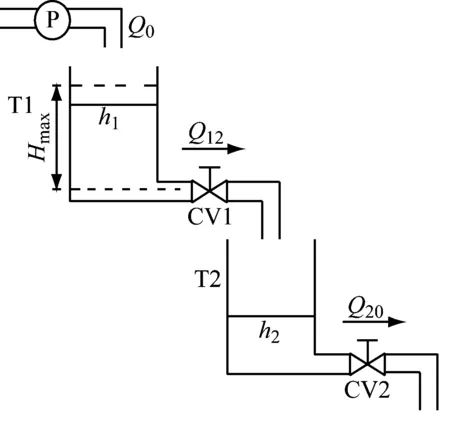
图2 双容水箱实验系统原理图

2 THPFSY-2型双容水箱T-S模糊建模

根据物料平衡原理可得[5]：

水箱T1

水箱T2

由托里拆利公式[6]：

整理可得：

(1)

经过多次实验，选用4条规则(M1～M4)给双容水箱实验系统建模。

Rule 1：IFh1(t) is about 0.2Hmax，THEN

Rule 2：IFh1(t) is about 0.4Hmax，THEN

Rule 3：IFh1(t) is about 0.6Hmax，THEN

Rule 4：IFh1(t) is about 0.8Hmax，THEN

可得：

其隶属度函数[7]选择梯形和三角形，如图3所示。

图3 前提变量的隶属函数(4条规则)

令x=[x1x2]T=[h1h2]T，得到的双容水箱实验系统的T-S模型表示如下：

(8)

式中：ξ(t)=x1(t)/Hmax。将以上建立的T-S模糊模型与双容水箱的机理模型以水箱1液位40%稳态值为条件，在SIMULINK中仿真，仿真时间200 s，采样时间0.01 s，初始值x0=[0 0]T，u0=350 mL/s，其结果如图4所示。理论与实践均证明，随着模型规则数的增加，T-S模型可以任意给定精度逼近任一非线性系统。

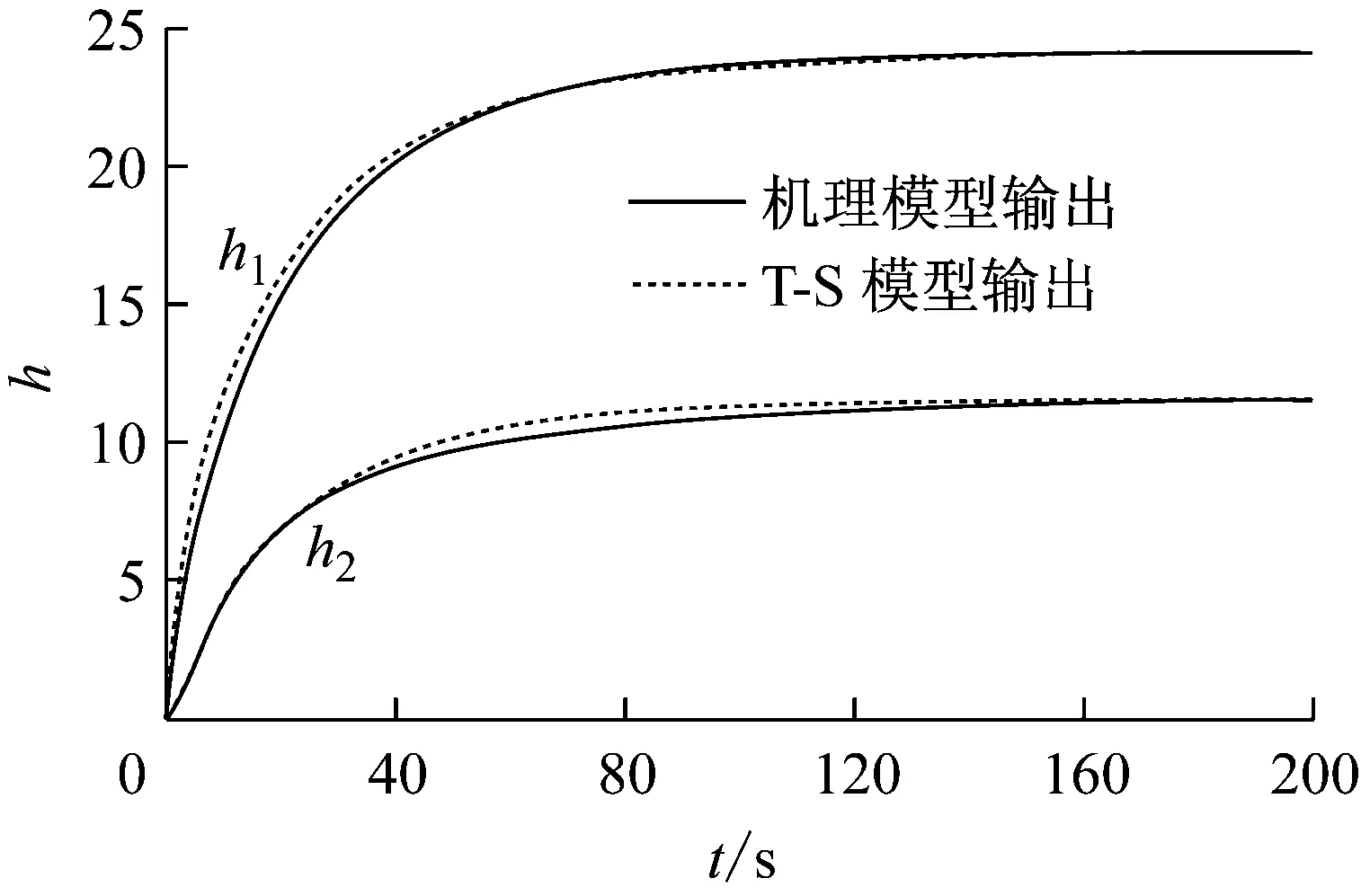
图4 T-S模型与机理模型对比

3 基于水箱T-S模型的故障诊断设计

一个连续时间系统的T-S模型受执行器故障、传感器故障以及噪声干扰时，其一般表达式[8]：

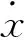
Eid(t)+Fif(t)]

Gid(t)+Rif(t)]

(9)

式中：ξ(t)为可测前提变量[9]；Ai∈Rn×n，Bi∈Rn×m，Ci∈Rq×n为系统状态矩阵；u(t)∈Rm为系统的控制量；Ei∈Rn×nd，Fi∈Rn×nf，Gi∈Rq×nd，Ri∈Rq×nf。对于式(9)表示T-S模型系统，则其基于故障检测滤波器[10]形式的残差生成器可用以下形式表示：

(10)

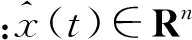
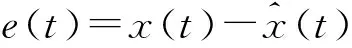
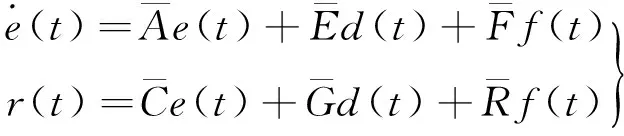
(11)

为书写方便，将前提变量ξ(t)简写为ξ，

(12)

(13)

(14)

(15)

(16)

(17)

此时，引入一个参考模型[11]，其传递函数可以用Wref表示，且该模型的输出rref(s)=Wreff(s)对故障f(t)有着较高的灵敏度，能够非常理想地跟踪并反映出故障特点，且满足：

(18)

此时的参考模型滤波器模型可以保证在所有的频域范围内对故障f(t)都有一定放大作用，有助于实现对故障的检测[11-12]。此时定义如下广义残差信号re(t)，其值为状态观测器所得到的残差与参考模型输出的差，其频域表达式为：

re(s)=r(s)-Wreff(s)

(19)

假设选择一个合适的Wref∈RH∞，其状态实现为:

(20)

式中，Dref∈Rnr×nf，若定义增广向量

则根据式(19)及式(20)可得以下增广残差状态方程：

(21)

式中：

定理式(10)的残差生成器设计可转化为以下线性不等式(LMI)条件下最优化问题：

(26)

式中：P1、P2为正定对称矩阵；Ki、V为适当维数的矩阵；γ为一正数，需满足以下LMI条件：

(27)

其中，Ψij定义如下：

(28)

*代表对应位置元素的转置，φij表示如下：

(29)

解以上LMI不等式组即可直接得到残差加权矩阵V，而观测器增益矩阵为

(30)

得到的γ表征了故障诊断的鲁棒性能，γ越小，故障诊断的鲁棒性越好。

(31)

若正定对称矩阵P可以用正定对称矩阵P1、P2表示为：

(32)

将式(22)～(25)以及式(32)代入式(31)，可以得到：

(33)

式中，Ψij定义如式(28)。参照文献[15]中的结论，不等式(33)成立的充分条件是以下不等式成立：

证毕

一般情况下，取Ei=E，Fi=F，Gi=G，Ri=R。此时有Ψii=Ψij，则条件式(27)可以简写为：

Ψii<0,i=1,2,…,r

(34)

4 THPFSY-2型水箱故障诊断

4.1 系统描述

在故障及干扰情况下，水箱其连续时间系统T-S方程可表示如下：

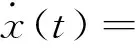
Eid(t)+Fif(t)]

(35)

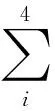
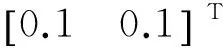
(36)

4.2 故障诊断仿真

实际故障f(t)包含fa(t)及fs(t)两个故障，根据残差生成器设计部分的讨论，选取合适的参考模型Wref可得到二维残差r(t)，其每一行的元素分别对应fa(t)及fs(t)，因此可同时检测fa(t)及fs(t)。若Wref=Cref(SI-Aref)-1Bref+Dref，其状态空间实现可记为：

(37)

取

此时，根据Wref生成的残差r(t)可以同时实现对故障fa(t)及fs(t)的检测。根据定理得到一组最优解为γ=0.369 4，Jth=0.38。此时r(t)的每一路残差分别对应fa(t)和fs(t)，其仿真结果如图5所示。

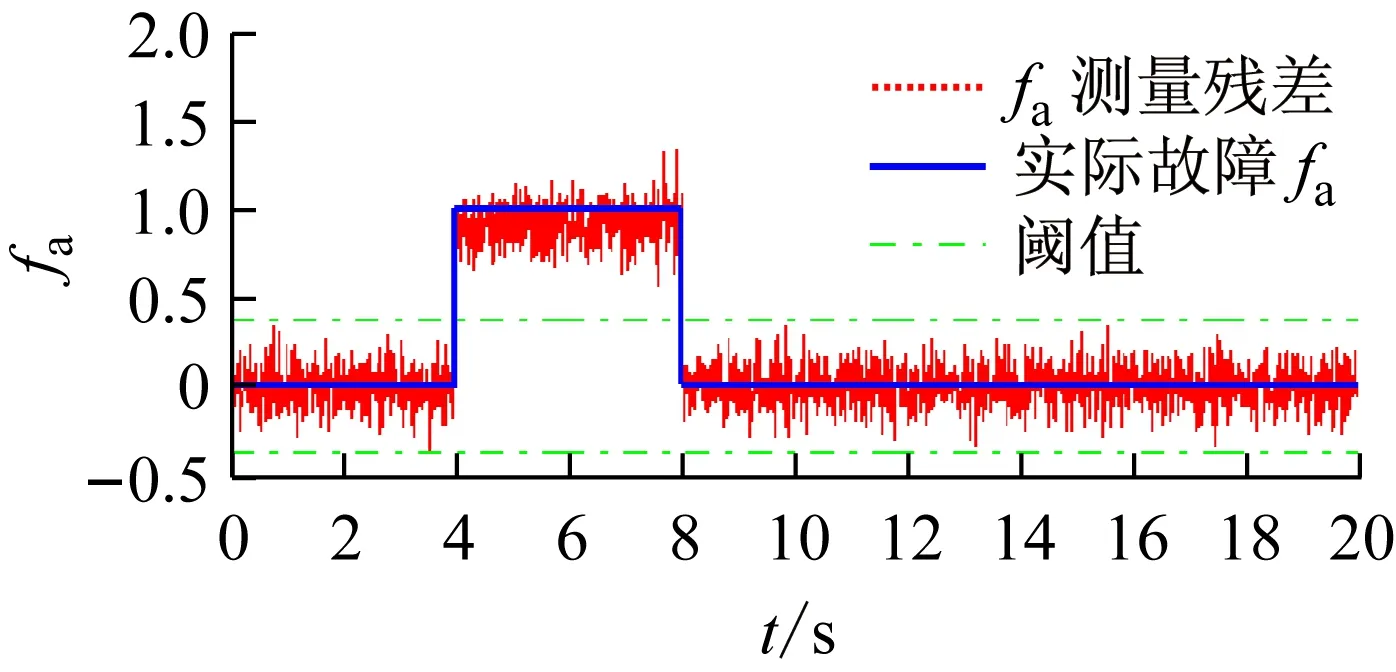
图5 fa(t)及fs(t)同时诊断

5 结语

针对双容水箱T-S模型，提出了一种基于参考模型的鲁棒残差生成器设计方法，不仅可以实现对水箱传感器故障的诊断及估计，对于相对复杂的执行器故障，依然可以利用本文所提方法进行诊断及估计。最后通过BRL引理将最优参数的求法用求LMI不等式组的方式表示出来，从而方便了计算。其算法的优点就是可以选择不同结构形式的参考模型来调整最终残差的结构，使其完成对每一类的故障分别建立相应的诊断残差，非常地灵活。

[1] 张也维, 范家璐. 基于重构贡献的双容水箱故障诊断方法 [J]. 解放军理工大学学报(自然科学版), 2014, 15(2): 103-8.

[2] 徐国旺, 沈毅. 三容水箱系统故障诊断算法研究 [D].哈尔滨：哈尔滨工业大学, 2008.

[3] 刘玲, 张西, 汪琳娜. 故障诊断技术的现状与发展 [J]. 电子测试, 2016(4): 62-63.

[4] THUMATI B T, FEINSTEIN M A, JAGANNATHAN S. A model-based fault detection and prognostics scheme for takagi-sugeno fuzzy systems [J]. IEEE Transactions on Fuzzy Systems, 2014, 22(4): 736-48.

[5] 吴丽娜. 基于模型的不确定系统鲁棒故障检测与估计方法研究 [D].哈尔滨：哈尔滨工业大学, 2013.

[6] 郎月. TS 模糊模型的建模研究 [D].锦州：渤海大学, 2014.

[7] 王振华, 沈毅, 张筱磊. 基于增广观测器的非线性系统执行器故障诊断 [J]. 宇航学报, 2012(12): 1742-6.

[8] ZHANG K, JIANG B, STAROSWIECKI M. Dynamic output feedback-fault tolerant controller design for Takagi-Sugeno fuzzy systems with actuator faults [J]. Fuzzy Systems, IEEE Transactions on, 2010, 18(1): 194-201.

[9] NGUANG S K, SHI P, DING S. Fault detection for uncertain fuzzy systems: an LMI approach [J]. IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1251-62.

[10] KHAN A Q, ABID M, DING S X. Fault detection filter design for discrete-time nonlinear systems— A mixed H- /H∞H- / H∞ math container loading mathjax optimization [J]. Systems & Control Letters, 2014, 67(1): 46-54.

[11] ICHALAL D, MARX B, RAGOT J,etal. Fault detection, isolation and estimation for Takagi-Sugeno nonlinear systems [J]. Journal of the Franklin Institute, 2014, 351(7): 3651-76.

[12] NAGY-KISS A M, SCHUTZ G, RAGOT J. Parameter estimation for uncertain systems based on fault diagnosis using Takagi-Sugeno model [J]. Isa Transactions, 2015, 56:65-74.

[13] BOULKROUNE B, HALABI S, ZEMOUCHE A. H-/H∞ fault detection filter for a class of nonlinear descriptor systems [J]. International Journal of Control, 2013, 86(2): 253-62.

[14] 钱华明, 富振铎, 宁秀丽. 基于LMI的H_/H∞故障检测观测器设计 [J]. 宇航学报, 2012, 33(12): 1747-56.

[15] TUAN H D, APKARIAN P, NARIKIYO T. Parameterized linear matrix inequality techniques in fuzzy control system design [J]. IEEE Transactions on Fuzzy Systems, 2001, 9(2): 324-32.

RobustFaultDiagnosisofTHPFSY-2Double-TankWaterLevelSystem

CHENHongli1,LIQiang2,LIUWenyan2

(1. College of Automation, Harbin Engineering University, Harbin 150001, China;2. Shang Institute of Satellite Engineering, Shanghai 201100, China)

The robust fault diagnosis of THPFSY-2double-tank under disturbance and fault was studied in this paper. According to the physical model of the double-tank system, a T-S fuzzy model of the system was established by local linear method. Then by introducing a reference model, a generalized residual error equation was established. At the same time, the problem of fault diagnosis was converted into a typical system robust control problem. Linear matrix inequalities (LMI) conditions for the optical solutions weregiven according to the bounded real lemma (BRL). Finally, effectiveness ofthe proposed algorithm was verified by Matlab simulation.

double-tank system; T-S model; robust fault diagnosis; linear matrix inequalities