Proteus在开关电阻调制跟踪滤波器设计中的应用

2017-12-15田社平

实验室研究与探索 2017年11期

关键词：支路滤波器波形

田社平，杨珏，方翔，张峰

(1. 上海交通大学电子信息与电气工程学院, 上海 200240； 2. 上海辛克试验机有限公司, 上海 201600)

Proteus在开关电阻调制跟踪滤波器设计中的应用

田社平1，杨珏2，方翔2，张峰1

(1. 上海交通大学电子信息与电气工程学院, 上海 200240； 2. 上海辛克试验机有限公司, 上海 201600)

中心频率自动可调的跟踪滤波电路是一种应用广泛的带通滤波电路。提出了一种基于开关与电阻串联调制方法的跟踪滤波器电路实现方法。开关电阻支路通过适当的电路连接方式并以一定的方式控制开关的通断，可产生所需要的等效电阻。从能量等效的角度给出了开关电阻支路等效电阻的计算方法。讨论了基于开关电阻调制的跟踪滤波器设计方法。设计了双二次结构的带通跟踪滤波器，该电路由1片四运放芯片AD713、2片模拟开关芯片DG418以及若干电阻、电容元件组成。采用Proteus对跟踪滤波器的特性进行测试，其结果与理论分析吻合，为跟踪滤波器的实际应用提供了可靠的依据。

开关电阻；调制；跟踪滤波器； Proteus软件

0 引言

滤波电路应用非常广泛，在许多测控电路中，被测信号的频率f在很宽的频带内变化，要求测量电路在很窄的f±Δf频带内提取测量信号。在这种情况下，必须采用中心频率自动可调的跟踪滤波电路来提取有用的测量信号而抑制无用的干扰信号。

实现跟踪滤波电路的方法有多种，如压控跟踪滤波电路[1-2]、开关电容跟踪滤波电路[3-6]、模拟乘法器跟踪滤波电路等[7-8]。实践中，可以自行搭接跟踪滤波电路，也可直接在市场中购买具有跟踪滤波功能的集成芯片来实现相应的滤波功能[9-11]。由于具有跟踪滤波功能的集成芯片工作模式固定等，有时不能满足实际的功能要求。本文给出了一种基于开关电阻调制的跟踪滤波电路设计方法，并通过电路仿真软件Proteus测试跟踪滤波电路的性能。

1 开关电阻调制方法

如图1(a)所示，开关S和电阻R构成串联支路，当S闭合时，从端口看进去的等效电阻Re为R；而当S断开时，Re则为∞。如果开关S采用模拟电子开关，在其控制闭合、断开的控制端施以如图1(b)所示的周期性数字控制信号，并假设控制信号为高电平时开关闭合，为低电平时开关断开，则可从能量等效的角度求出端口等效电阻Re。

(a) 开关电阻支路 (b) 周期性数字控制信号

图1 开关电阻调制

假设开关电阻支路端口电压为u，则在一个周期T内，开关电阻支路吸收的能量为

(1)

假设端口等效电阻为Re，则其在一个周期T内吸收的能量w=(u2/Re)T。由能量等效可求得开关电阻支路端口等效电阻为

Re=(T/TT)R=R/α

(2)

式中:α为周期性数字控制信号的占空比，也是开关S的通断比。

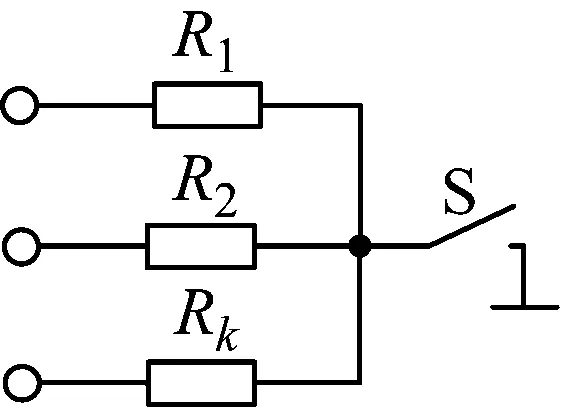
图2(a)所示为开关S与多个电阻连接，控制S通断的信号占空比为α，则图2(a)电路可等效为图2(b)电路，其中的等效电阻分别为

R1e=R1/α，R2e=R2/α，Rke=Rk/α

(3)

(a) (b)

图2 开关与多个电阻连接

2 跟踪滤波器的设计方法

图3为采用开关电阻调制方法实现的带通跟踪滤波器电路，它通过对双二次环滤波电路中的部分电阻进行开关调制来达到带通中心频率可调的目的[12]。

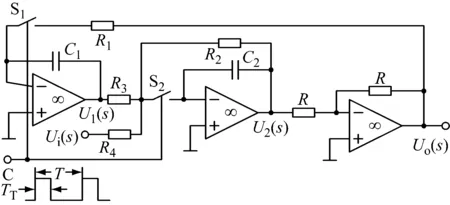
图3 基于开关电阻调制的带通跟踪滤波器

假设控制端C的信号周期为T，占空比为α，则在一个周期内，开关S1、S2闭合时间TT=αT，电阻R1受到开关S1的调制，R2～R4受到开关S2的调制，其等效电阻分别为

Rie=Ri/α=(T/TT)Ri,i=1,2,3,4

(4)

假设图3电路的作用是将频率为f以外的信号滤除，亦即带通的中心频率为f。为使得在一个周期内等效电阻的等效值尽量恒定，可取开关控制信号的频率为频率f的n倍(n为一较大的整数)。此时，式(4)可改写为:

(5)

式中:ω=2πf，为带通电路的中心角频率；fT=1/TT，称为全导通频率;ωT=2πfT，称为全导通角频率，为固定值。显然，当控制信号频率为fT时，Rie即为Ri。

由上面分析，可得图3电路的输入输出特性为

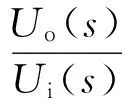
(6)

由式(6)可知，图3电路具有带通特性，且中心频率为

(7)

品质因数为

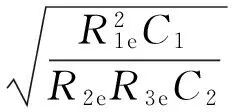
(8)

中心频率处的放大倍数为

(9)

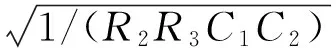
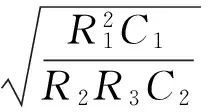
(10)

由式(10)可知，图3电路的带通中心频率处的放大倍数A与品质因素Q不随ω发生变化，为固定值，因此，图3电路具有带通跟踪滤波的功能。

3 基于Proteus的跟踪滤波性能测试

为验证跟踪滤波器的性能，采用电路仿真软件Proteus进行测试[13-14]。在Proteus环境中设计如图4所示的带通跟踪滤波器，电路采用双二次结构。该电路由1片四运放芯片AD713、2片模拟开关芯片DG418以及若干电阻、电容元件组成。图中参数：ωT=666.67 rad/s，TT=9.42 ms，品质因数Q=10，中心频率处的放大倍数A=1。

图4 带通跟踪滤波器实例

3.1 频率特性测试

取电路的带通中心频率f=40 Hz，倍频数n=100。在开关调制控制信号C端输入频率为4 kHz的矩形波开关控制信号，其脉宽为TT/n=94.2 μs。在输入信号端施加不同频率的正弦波，测量输出信号与输入信号的幅值比和相位差，绘制的频率特性曲线见图5。由图可见，电路具有良好的带通特性。

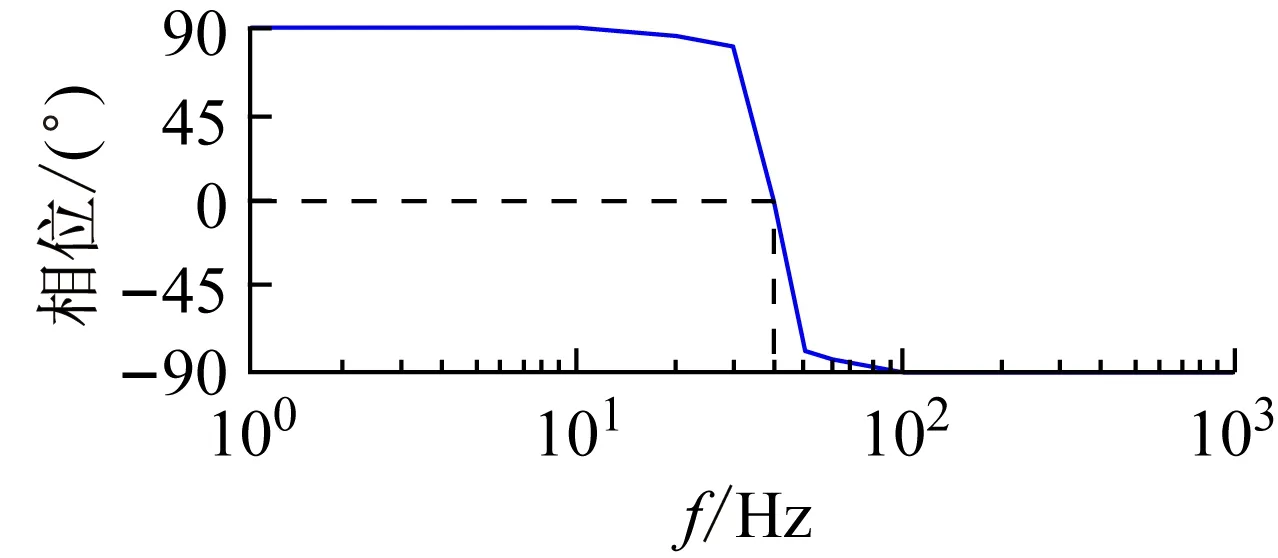
图5 带通中心频率f=40 Hz时的频率特性

3.2 倍频数n的选择

倍频数n的等效应合理选择，n太小，由于开关通断的切换导致波形光滑性差，出现锯齿波形；n太大，由于开关控制波形的脉宽与n呈反比，导致脉宽太窄，可能出现受模拟开关的响应时间限制而出现开关无法动作的情形。对图5电路，取电路的带通中心频率f=40 Hz，令n=20，则有TT/n=4.71 ms，在输入端施加振幅为10 V，频率为40 Hz的正弦波，其输出波形如图6(a)所示，可以明显看出波形中的锯齿成分；而令n=100时的输出波形如图6(b)所示，可以看出波形的光滑性得到较明显改善。在Proteus中通过改变n观察输出波形，发现当n=100左右时波形的光滑性和模拟开关的响应性能都比较满意。本文将该电路应用于转子动平衡测量系统中，取n=100得到了满意的效果[15]。

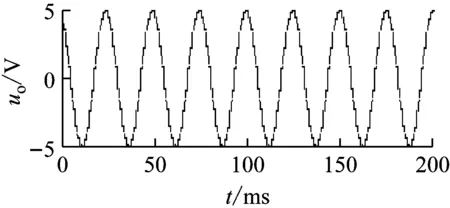
(a)n=20

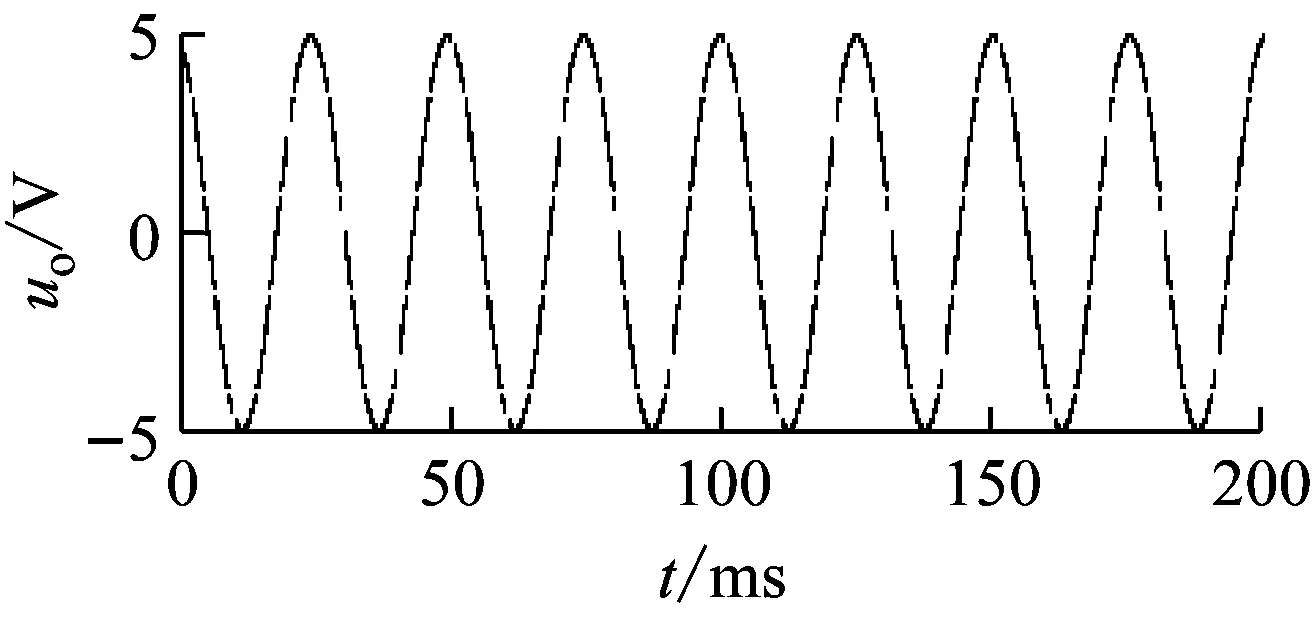
(b)n=100

图6 倍频数n的选择

3.3 滤波性能测试

带通滤波的目的是去除干扰信号，提取频率为滤波器中心频率的有用正弦信号。采用Proteus进行滤波性能测试的方法如下：在图4电路中的输入信号端[R4(1)]施加混有随机干扰的正弦波信号(通过合成理想正弦信号和正态分布噪声信号而得到的数据文件)，在输出信号端观察波形。

图7给出仿真测试结果，其中输入信号

ui=50sin(2π×40t)+n(t)

n(t)为均值为零，标准差为50的正态分布噪声，单位为mV，亦即输入信号的信噪比为0 dB。uo为输出信号。由图可以看出，由于电路的品质因数Q=10，为一较大值，故电路基本上可以完全滤除干扰信号，uo的振幅略低于50 mV，说明电路具有良好的带通滤波性能。

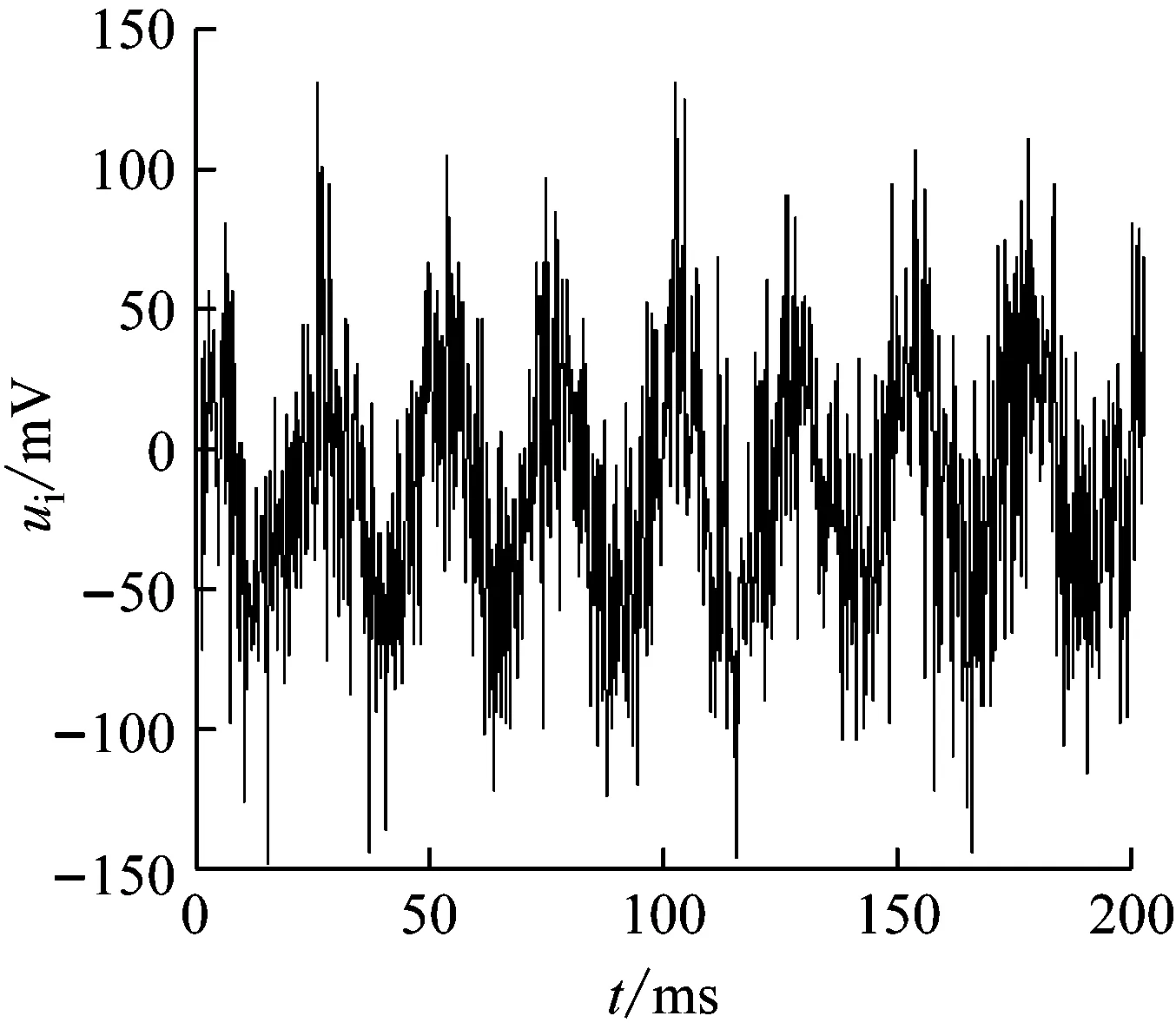
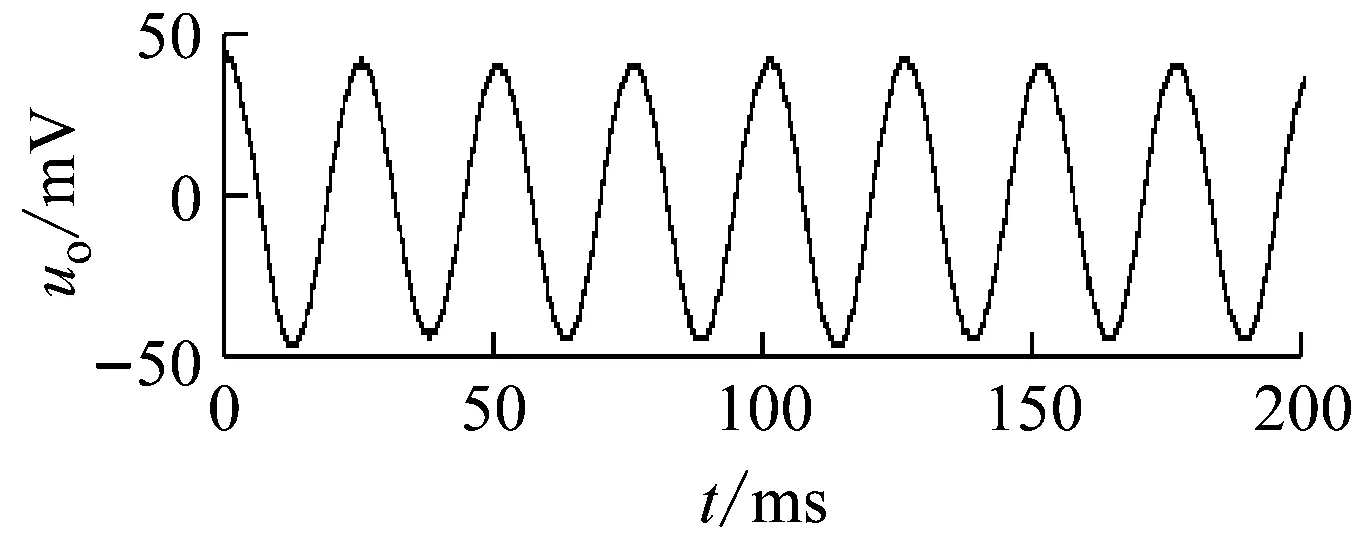
图7 滤波性能测试

4 结语

提出了一种基于开关电阻调制的带通跟踪滤波器的设计与实现方法，并采用Proteus软件对电路性能进行了仿真测算，极大地提高设计分析效率，为电路的实际应用奠定了坚实的基础。采用Proteus进行电路性能测试的优点在于电路设计过程简单，试验测量方便，而且仿真测试结果与电路实际应用结果也十分吻合。

[1] 张国雄. 测控电路[M]. 4版，北京：机械工业出版社， 2011.

[2] 李晓鹏，徐静, 李矩, 等. 压控跟踪滤波器原理与实现方法[J]. 现代制造工程，2006(6)：114-115.

[3] 彭永棒，孙奉娄，蓝加平，等. 基于CPLD 的开关电容组式跟踪滤波器设计与实现[J]. 微型机与应用，2013，32(3)：19-22.

[4] 陈怀超, 丛培田. 基于开关电容的自动跟踪滤波器的设计及研究[J]. 仪表技术与传感器，2003(10)：38-39.

[5] 林涛. 开关电容跟踪滤波器的研究[J]. 西安公路学院学报，1995，15(1)：97-99.

[6] 陈照章. 跟踪滤波器的设计及其应用[J]. 仪器仪表学报，2001，22(3)：244-246.

[7] 丛培田，华雷，田明德，等. 模拟乘法器式自动跟踪滤波器设计与研究[J].沈阳工业学院学报，1993，12(4)：25-29.

[8] 陶利民, 肖定邦, 温熙森. 用于动平衡测试的MDAC窄带跟踪滤波器[J]. 国防科技大学学报，2006，28(2)：102-105.

[9] 于巍巍, 颜德田, 杨樾. 基于MAX260 的自动跟踪滤波器的工程设计与应用[J]. 现代电子技术，2008，16(5)：76-78.

[10] 李旭涛，丁国清. 基于MAX268的自动跟踪滤波器的研究及应用[J]. 电测与仪表，2006，43(3)：62-64.

[11] 张建峡, 徐云, 张凯洪, 等. 自适应信号分解实验装置[J]. 实验技术与管理，2011，28(3)：66-68.

[12] 田社平，秦琳. 基于脉宽调制的双二次环跟踪带通积分电路及其控制方法[P]. 中国专利：ZL2010105011555.3，2014-05-21.

[13] 闫俊荣，崔霞，张彩荣. 滤波器的频率特性仿真实验研究[J]. 实验技术与管理，2012，29(1)：86-88.

[14] 刘德全. Proteus 8-电子线路设计与仿真[M]. 北京：清华大学出版社，2014.

[15] 俞水锋，杨珏，林晓娟，等. 基于数字陷波滤波器的转子不平衡量测量[J]. 计量技术，2011(10)：15-18.

ApplicationofProteusinModulationofSwitchingResistorsinTrackingFilterDesign

TIANSheping1,YANGJue2,FANGXiang2,ZHANGFeng1

(1. School of Electronic, Information and Electrical Engineering, Shanghai JiaoTong University, Shanghai 200240, China; 2. Shanghai Schiak Testing Machinery Co., Ltd.， Shanghai 201600， China)

The tracking filter with automatically adjustable center frequency is a widely used band-pass filter circuit. A realization method of the tracking filter circuitis is proposed based on modulation of switching resistors. The desired equivalent resistance can be obtained through appropriate circuitry and control of switch mode. The equivalent resistance can be computed through energy equivalence theory. The design of tracking filter based on modulated switching resistors is discussed. A tracking filter with biquadratic structure is designed. The filter is composed of a four op-amp chip (AD713), two single-pole/single-throw analog switch chips (DG418) and some resistors and capacitors. Proteus software is applied to measure the characteristics of the tracking filter, and the simulation results coincide with those of theoretical analysis.The method provides a reliable basis for the application of the tracking filter.

switching resistor; modulation; tracking filter; Proteus software