基于多密钥同态技术的安全多方计算协议*

王会勇 冯勇 赵岭忠 唐士杰

(1．中国科学院大学 成都计算机应用研究所， 四川 成都 610041； 2．桂林电子科技大学 数学与计算科学学院， 广西 桂林 541004；3．中国科学院重庆绿色智能技术研究院 自动推理与认知重庆市重点实验室, 重庆 400714；4．桂林电子科技大学 广西可信软件重点实验室， 广西 桂林 541004)

基于多密钥同态技术的安全多方计算协议*

王会勇1,2冯勇3赵岭忠4唐士杰4

(1．中国科学院大学 成都计算机应用研究所， 四川 成都 610041；
2．桂林电子科技大学 数学与计算科学学院， 广西 桂林 541004；
3．中国科学院重庆绿色智能技术研究院 自动推理与认知重庆市重点实验室, 重庆 400714；
4．桂林电子科技大学 广西可信软件重点实验室， 广西 桂林 541004)

为构造具有良好性能的多密钥安全多方计算(SMC)协议，对Gentry-Sahai-Waters(GSW13)全同态加密(FHE)方案的密钥同态性质进行了研究. 在此基础上提出了一个基于GSW13方案的层次型多密钥SMC协议，该协议构造方式简单，只需要3轮通信，且在半诚实与半恶意环境和公共随机串模型下，其安全性可以归结到容错学习问题(LWE)和它的一个变种问题；分析了该变种问题的困难性，并给出了半恶意模型下该协议的形式化安全证明. 该协议自然构成一个相同环境下的层次型多密钥全同态加密方案. 对比分析表明，文中协议在整体性能上优于已有方案.

安全多方计算；多密钥全同态加密；密钥同态；门限解密；GSW13

安全多方计算(SMC)概念来源于Yao[1]提出的安全两方数据比较问题(百万富翁问题)，旨在解决多个参与者联合保密计算某个函数的问题.

1987年，Goldreich等[2]提出了可计算任意函数的基于密码学安全模型的安全多方计算协议，并于1988年提出了SMC的安全性定义.目前，对SMC的研究主要集中在一般方案与特殊方案两个方向[3]，研究内容主要包括不同环境(半诚信、半恶意及恶意环境)和不同信道(同步或异步信道)下的方案，研究工具主要有可验证秘密共享(VSS)[4- 6]、不经意传输(OT)[7- 8]、同态加密(HE)[9- 11]和混合匹配[12]等.其中，同态加密技术在SMC设计中显示了良好的潜力，受到越来越多关注.

全同态加密(FHE)思想是由Rivest等[13]在1978年提出的.2009年，Gentry[14]构造出第一个FHE方案.其后出现了多种方案，如DGHV10方案[15]、BV11方案[16]、BGV12方案[17]、GSW13方案[18]、NK15方案[19]等.目前，学界针对基于FHE技术的SMC方案开展了大量的研究.

Lóopez-Alt等[9]提出了多密钥全同态加密(MFHE)概念，同时给出了一个“洋葱式”的MFHE构造思路，并利用该思路和改进的NTRU加密方案[20]构造了一个可以“离线”运行(On-the-fly)的MFHE协议.该方案的主要优点是构造过程不依赖于具体的FHE方案，缺点是加解密复杂度太高，且方案复杂度随用户数量呈指数增长.

文献[10,21]给出了构造MFHE方案和SMC协议的另一种方式.其基本思路是将GSW13方案的密文矩阵通过级联方式组成联合密文矩阵，同时将相应密钥组合成联合密钥进行加密与解密.其主要缺点是通过级联方式构造出的密文矩阵体积很大，且构造过程需要计算额外的掩盖信息.

Asharov等[11]提出了门限FHE的概念，并构造了一种只需两轮交互的MFHE方案和对应的SMC协议.与以前方案相比，其优点是加解密运算复杂度低.主要缺点是构造过程依赖于Bv11[16]与BGV12[17]方案，而这两个方案在进行同态乘法时的密文膨胀率很高且需要运行密钥.

为充分利用GSW13方案的优点，文中研究了其密钥同态性质，在此基础上构造了一个层次型多密钥SMC协议.该协议使用门限式解密，在半诚信、半恶意环境和公共随机串(CRS)模型下的安全性可以归结到容错学习问题(LWE)及该问题的一个变种问题(Some-are-errorless LWE)上.研究了该问题的困难性，并给出了半恶意环境下的形式化安全性证明.由该协议的构造过程可以自然抽象出一个多密钥FHE方案.

1 预备知识

1.1 符号与基础概念

1.1.1 符号

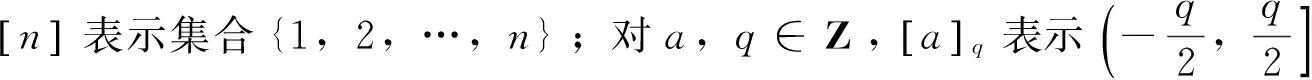
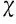
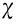
(1)

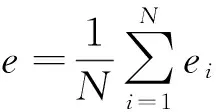
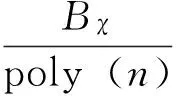
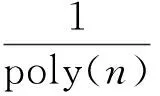
故知结论成立.

1.2 安全多方计算

1.2.1 一般定义

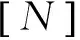
1.2.2 计算模型

SMC的计算模型分为半诚实、半恶意和恶意3种情况.在半诚实模型下，参与计算者会严格按照协议操作，不会主动更改协议或数据.但可能保留中间计算结果，用于推算其他用户的私有数据.

半恶意模型可以被看成一个交互式图灵机(ITM)，除拥有标准磁带外，还拥有一个证据磁带.在协议的任何时刻，半恶意敌手必须将它代表某个用户发出的任何信息记录到证据磁带上.该敌手根据输入和一定随机性来决定是否忠实履行原协议.

恶意模型是指模型中的参与方可以任意篡改、泄露协议和数据，甚至可以阻止协议的正常执行.

任意半恶意模型下的SMC协议都可以借助于非交换的零知识证明(NIZKs)等工具转化为恶意模型下的协议[11].因此，文中只在半诚实和半恶意模型下考虑所设计SMC协议的安全性.

2 Some-are-errorless LWE问题

LWE问题已经成为多个密码学源语的困难性基础.Regev[22]首先给出了该问题的一个量子规约.Brakerski等[23]首次给出了该问题的一个多项式规约，并讨论了带有一个等式约束的LWE问题(被称为First-is-errorless LWE)的困难性.将该概念进行扩展，考虑有多个等式约束的LWE问题的困难性.这是构建多密钥SMC协议的一个安全性基础.

定义1 Some-are-errorless LWE

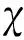
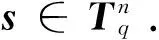
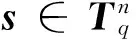
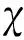
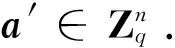
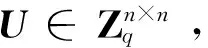
(1)利用扩展欧几里得算法构造一个幺模矩阵R，满足Ra′=(r,0,0,…,0)T.

(2)记U=R-1·diag(r,1,…,1).

由R为幺模矩阵且Ra′=(r,0,0,…,0)T，知R可逆且有：R-1Ra′=a′=R-1(r,0,0,…,0)T，即a′为矩阵R-1的最左一列乘r.

而U=R-1·diag(r,1,…,1)即为将R-1的最左一列乘r，其他元素不变.故U为满足条件的矩阵.

均匀选取l个元素s0,s1,…,sl-1∈Zq，然后按照如下步骤构建规约过程，其中i=0,1,2,…,l-1.

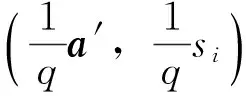
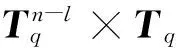
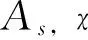
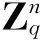
若q为素数，该规约最多将成功优势降低q-n.若q不是素数，则成功优势的损失最大为

(3)

这表明只要n足够大，该规约的成功优势损失是可忽略的，即LWEn,l,q,χ问题的困难性可以与LWEn-l,q,χ问题相同.

3 GSW13方案的密钥同态性质

Boneh等[24]对具有密钥同态性质的伪随机函数进行了研究，其基本定义如下.

3.1 密钥同态

定义2 (密钥同态伪随机函数[24]).设F:K×X→Y是一个伪随机函数(PRF)，其密钥空间K具有群结构并具有某种群运算⊕；X和Y分别是明文和密文空间.称F是密钥同态的，若对任意k1,k2∈K，由F(k1,x)和F(k2,x)能找到某有效算法计算F(k1⊕k2,x).

现对该定义进行扩展，并将密钥数量扩展到N.

定义3 对某公钥加密方案E，设(pki,ski)为有效的公钥/私钥对.若对pk=f(pk1,pk2,…,pkN)，能找到sk=g(sk1,sk2,…,skN)，使(pk,sk)也是E的有效密钥对，则称E具有密钥同态性质，其中f和g为可有效计算的函数.特别地，若f和g都是求和(乘积)函数，称E具有密钥加(乘)同态性质；若f和g都是线性函数，则称E具有密钥线性同态性质.

3.2 GSW13方案的密钥同态性质

3.2.1 GSW13方案

GSW13方案是基于容错学习(LWE)问题的FHE方案.文中将利用该方案作为构造多密钥SMC协议的基础.为了叙述的简洁性，文中使用文献[25]的方式来描述该方案.

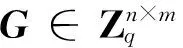
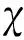
GSW.Encrypt：对明文μ，构造均匀随机矩阵R∈{0,1}m×m，计算C=AR+μG.

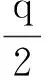
GSW.Evaluation：对两个输入密文C1和C2，其同态加法、乘法和与非门(NAND)运算可以定义为：

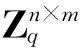
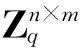
NAND(C1,C2): OutputG-C1G-1(C2).

正确性：由公钥的构造方式可知有tA=e≈0成立.故tC=tAR+μtG≈μtG.故有：

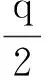
3.2.2 密钥同态性质

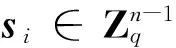
证明：可知有

成立.故仍有tC=tAR+μtG≈μtG.因此按原方案解密可得到明文μ.故在B不变的情况下，该方案是密钥线性同态的.

4 基于GSW13的SMC方案

4.1 基于层次型GSW13方案的SMC协议

GSW13方案的基础方案是层次型的，即只能做有限次同态运算.要去除此限制，目前只能借助于自举技术，但自举技术会破坏GSW13方案的大部分优势.因此文中将构造基于层次型GSW13方案的SMC协议.以下叙述中，i∈[N].

协议πf：分布式半诚实及半恶意环境和CRS模式下，安全计算单值函数f的协议.

输入：用户数量N(其中第i个用户的标识为Pi)；用户Pi拥有隐私数据μi∈{0,1}.一个确定性PPT可计算函数f:{0,1}N→{0,1}，被表示为一个仅包含与非门(NAND)的布尔电路Cir，其与非门电路最大深度为d.

输出：μ=f(μ1,μ2,…,μN).

步骤1 参数设置Setup(1λ,1d)，包含两个操作.

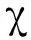
步骤2 密钥生成：用户Pi执行如下算法.

步骤3 联合公钥生成及加密：每个用户公开自己的公钥pki并接收他人公钥，执行如下操作：

(1)生成联合公钥.所有用户计算：

步骤4 同态运算：所有用户在得到其他用户的密文矩阵Ci后，执行同态计算：

其同态加法、乘法和与非门(NAND)运算定义与GSW13方案相同.

步骤5 门限式(Threshold)解密：所有用户执行如下操作.

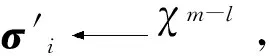
(2)得到所有ωi之后，计算：

其中t为隐含的公用私钥，不显式出现.

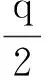
上述过程同时给出了一个MFHE方案.

4.2 正确性

该协议的正确性主要依赖于两个方面.

首先，GSW13方案的正确性已经得到证明，故只需考察所用参数是否正确.其次，由原方案知，按上述参数设置，该方案在进行d层与非门同态运算之后的噪音不超过((n+1)·l+1)dBχ.因此，只要q/Bχ>8((n+1)·l+1)d，就能保证进行d层与非门同态运算后的误差(由v=ωG-1(wT)得到的v与μ的距离)不超过q/8，从而可以通过模q得到正确结果.

其次，协议的加解密正确性主要涉及3个问题.

(1)公用密钥对的正确性.协议πf所用密钥对的有效性已经由定理1.1得到证明.

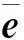
(3)联合解密的正确性.首先，联合密钥对的合法性已经得到证明，即若有C=Enc(pk,μ)，则必有μ=Dec(sk,C).其次，由步骤5知：

由此可得：

ωG-1(wT)=(tC+σ)G-1(wT)=

tCG-1(wT)+σG-1(wT)=

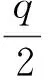
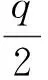
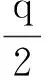
4.3 安全性

4.3.1 半诚实模型下的安全性

在半诚实模型和公共随机串(CRS)模式下，文中协议的安全性基于以下几个问题.

(1)在上述设置下，GSW13基本方案的安全性可以归结为容错学习问题LWEn,q,χ.

(2)部分解密结果的安全性.由步骤5可知，在等式ωi=ti·C+σi与ω=tC+σ中，ti和t为私钥，ti·C和t·C运算等价于向量内积运算，且σi和σ的前l个分量是服从Bχ-有界分布的，因此这两个等式构成了Some-are-errorless LWE问题，从而公布部分解密结果不会泄露用户隐私数据及私钥ti和隐含密钥t.

4.3.2 半恶意模型下的安全性

半恶意模型下的安全威胁主要来自于合谋(串谋)攻击，即多个用户合作利用其私有数据和公有数据，试图获得其他用户的私有数据.以下将考虑极端情况，即所有N个用户中只有一个诚实用户Ph，其他N-1个半恶意用户合作攻击Ph.

定理5 设f为一个具有N个输入和1个输出的多项式时间(PPT)可计算的确定性函数.则上述协议πf能够在存在一个俘获了N-1个用户的静态半恶意敌手A的情况下实现f.

证明：首先设计一个针对上述半恶意敌手A的PPT模拟器S.设唯一的诚实用户为Ph,该模拟器代表Ph执行如下操作.

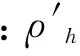
最后，模拟器S将上述模拟部分解密结果公布.

游戏REALπ,A,Z：该游戏即在具有一个半恶意敌手A的真实环境Z中对协议πf的忠实执行过程.

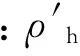
游戏IDEALF,S,Z：在该游戏中，用户Ph将对0加密得到的密文代替其私有数据的密文进行公布，其它操作与HYBπ,A,Z一样.

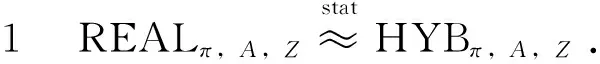
证明：模拟器S利用除Ph的真实部分解密结果之外的信息(包括最终计算结果μ)来模拟计算Ph的部分解密结果，因此若设v=μ「q/2⎤+e′，则其模拟算法应该为

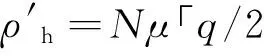
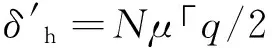
(4)

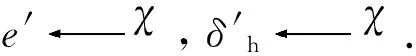
ρh=ωhG-1(wT)+δh=vh+δh

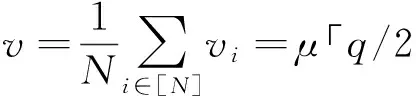
ρh=vh+δh=

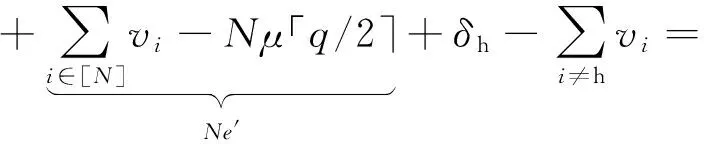
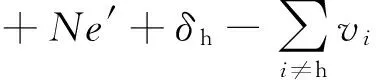
(5)

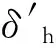
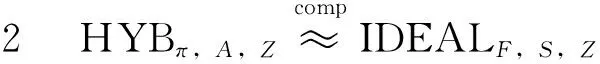
证明：这两个游戏的唯一区别在于Ph公布的密文Ch是对其真实私有数据的加密还是对0的加密.但其加密方式的语义安全性已经被证明[18]，故在这两种情况下的加密结果是计算上不可区分的，从而可以推断这两个游戏也是计算上不可区分的.

4.4 协议性能分析及对比

文中协议只需要3轮交互操作:第一轮是个人密钥对的生成、发布与接收； 第二轮是公用密钥对的生成、密文的发布与接收；第三轮是联合解密.

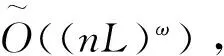
在空间效率上，由于GSW13方案的密文是矩阵，故在同态乘法中的密文膨胀率较小.而文献[11]方案的密文是向量，同态乘法会造成密文维数膨胀，对其空间效率造成极大影响.文献[10, 21]虽然也采用了GSW13方案作为基础，但其联合密文是用密文级联的方式构造的，因此需占用很大空间.

表1为几个基于FHE的SMC方案的性能对比.可以看出，文中方案在时间、空间效率等主要性能上优于已有方案.表中ε∈(0,1)，n为所用格的维数，q∈Z为模，Bχ∈Z为误差分布边界，N为参与计算的用户数，l=⎣logq」+1，U=(n+1)·l+1.

表1 几个基于全同态加密技术的安全多方计算方案主要性能对比

5 结语

基于GSW13全同态加密方案构造了一个层次型多密钥安全多方计算协议.该协议构造简单，只需要3轮通讯，且在半诚实与半恶意环境和公共随机串(CRS)模型下，其安全性可以归结到容错学习问题和它的一个变种问题(记为Some-are-errorless LWE)；将该协议与已有协议进行了对比，结果表明：该协议具有加解密复杂度低、密文膨胀率小、且不需要运行密钥等优点，整体性能优于现有基于FHE技术的SMC方案.

但该方案仍存在以下不足，值得深入研究.首先，GSW13方案的效率仍未达到实用要求，故可对其进行并行化处理[26]，以提高整体效率；其次，在网络协议的执行过程中，应采用合适的方式[27]保证数据的安全传输和会话的协同性要求.

[1] YAO A.Protocols for secure computations [C]∥Proceedings of the 23rd Annual Symposium on Foundations of Computer Science.New York:IEEE Computer Society,1982:160- 164.

[2] GOLDREICH O,MICALI S,WIGDERSON A.How to play any mental game [C]∥Proceedings of the 19th Annual ACM Symposium on Theory of Computing.New York:ACM,1987:218- 229.

[3] 范红,冯登国.安全协议理论与方法 [M].北京:科学出版社,2003.

[4] CRAMER R,DAMGARDI,MAURER U.General secure multi-party computation from any linear secret-sharing scheme [C]∥Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques.Bengaluru:Springer-Verlag,2000:316- 334.

[5] 唐韶华,马卫华.一种安全的分布式用户认证方案 [J].华南理工大学学报(自然科学版),1999,27(6):1- 5.

TANG Shao-hua,MA Wei-hua.A Distributed user authhentication schemes for security [J].Journal of South China University of Technology(Natural Science Edition),1999,27(6):1- 5.

[6] CHEN H,CRAMER R.Algebraic geometric secret sharing schemes and secure multi-party computations over small fields[C]∥Advances in Cryptology-CRYPTO 2006.California:Springer,2006:521- 536.

[7] CREPEAU C,vAN DE Graaf,TAPP A.Committed oblivious transfer and private multi-party computation [C]∥Advances in Cryptology-CRYPT0’ 95.California:Sprin-ger,1995:110- 123.

[8] DU W,ZHAN Z.A practical approach to solve Secure Multi-party Computation problems [C]∥Proceedings of the 2002 Workshop on New Security Paradigms.Virginia:ACM,2002:127- 135.

[10] CLEAR M,MCGOLDRICK C.Multi-identity and Multi-key leveled FHE from learning with errors [C]∥Advances in CRYPTO 2015.Berlin:Springer,2015:630- 656.

[11] ASHAROV G,JAIN A,LOPEZ-Alt A, et al Multiparty computation with low communication,computation and interaction via threshold FHE [C]∥Advances in Cryptology-EUROCRYPT 2012.Berlin:Springer,2012:483- 501.

[12] PANG L,SUN J F,LUO S S,et al.A research of the privacy preserving architecture of electronic auction [J].Journal of Convergence Information Technology,2012,7(1):172- 179.

[13] RIVEST R L,ADIEMAN L,DERTOUZOS M L.On data banks and privacy homomorphisms [J].Foundations of Secure Computation,1978,4(11):169- 180.

[14] GENTRY C.Fully homomorphic encryption using ideal lattices [C]∥The 41st ACM Symposium on Theory of Computing.Washington:ACM,2009:169- 178.

[15] VAN DIJK M,GENTRY C,HALEVI S,et al.Fully homomorphic encryption over the integers [C]∥Advances in Cryptology-EUROCRYPT 2010.Riviera:Springer,2010:24- 43.

[16] BRAKERSKI Z,VAIKUNTANATHAN V.Efficient fully homomorphic encryption from(standard) LWE [J].SIAM Journal on Computing,2014,43(2):831- 871.

[17] BRAKERSKI Z,GENTRY C,VAIKUNTANATHEAN V.(Leveled) Fully homomorphic encryption without bootstrapping [C]∥Proceedings of the 3rd Innovations in Theoretical Computer Science Conference.Massachusetts:ACM,2012:309- 325.

[18] GENTRY C,SAHAI A,WATERS B.Homomorphic encryption from learning with errors:conceptually-simpler,asymptotically-faster,attribute-based [C]∥Advances in CRYPTO 2013.California:Springer,2013:75- 92.

[19] NUIDA K,KUROSAWA K.(Batch) Fully homomorphic encryption over Integers for non-binary message spaces [C]∥Advances in Cryptology-EUROCRYPT 2015.Berlin:Springer,2015:537- 555.

[20] STEHLE D,STEINFELD R.Making NTRU as secure as worst-case problems over ideal lattices [C]∥Advances in Cryptology-EUROCRYPT 2011.Tallinn:Springer,2011:27- 47.

[21] MUKHERJEE P,WICHS D.Two round multiparty computation via multi-key FHE [C]∥Annual International Conference on the Theory and Applications of Cryptographic Techniques.Berlin:Springer,2016:735- 763.

[22] REGEV O.On lattices,learning with errors,random linear codes,and cryptography [J].Journal of the ACM,2009,56(6):1- 40.

[23] BRAKERSKI Z,LANGLOIS A,PEIKERT C.Classical hardness of learning with errors [C]∥ACM Symposium on Theory of Computing.New York:ACM,2013:575- 584.

[24] BONEH D,LEWI K,MONTGOMERY H,et al.Key homomorphic PRFs and their applications [C]∥Advances in Cryptology-CRYPTO 2013.California:Springer,2013:410- 428.

[25] ALPERIN-SHERIFF J,PEIKERT C.Faster bootstrapping with polynomial error [C]∥Advances in Cryptology-CRYPTO 2014.California:Springer,2014:297- 314.

[26] HIROMASA R,ABE M,OKAMOTO T.Packing messages and optimizing bootstrapping in GSW-FHE [C]∥Public-Key Cryptography-PKC 2015.Gaithersburg:Springer,2015:699- 715.

[27] 刘巍巍,周来水,庄海军,等.一种基于Internet的同步协同CAD/CAM系统的安全机制 [J].华南理工大学学报(自然科学版),2005,33(9):20- 24.

LIU Wei-wei,ZHOU Lai-shui,ZHUANG Hai-jun,et al.A security mechanism for internet-based synchronous collaborative CAD/CAM system [J].Journal of South China University of Technology(Natural Science Edition),2005,33(9):20- 24.

ASecureMulti-PartyComputationProtocolontheBasisofMulti-KeyHomomorphism

WANGHui-yong1,2FENGYong3ZHAOLing-zhong4TANGShi-jie4

(1. Chengdu Institute of Computer Applications, University of Chinese Academy of Sciences, Chengdu 610041, Sichuan, China; 2. School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China; 3. Chongqing Key Laboratory of Automatic reasoning and Cognition, Chongqing Institute of Green Intelligent Technology, Chinese Academy of Sciences, Chongqing 400714, China; 4. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China)

In order to build a multi-key secure multi-party computation (SMC) protocol with high performance, the key homomorphic properties of Gentry-Sahai-Waters (GSW13) fully-homomorphic encryption (FHE) scheme is investigated. Afterwards, a general multi-key SMC protocol with simple structure, which needs only 3 rounds of interactions, is proposed on the basis of leveled GSW13. In the semi-honesty and semi-malicious setting as well as in the common random string model, the security of the protocol relies on the learning with errors (LWE) problem and a variant of LWE. Then, the difficulty in solving the variant is analyzed, and a formalized security proof in semi-malicious setting is given. The proposed SMC protocol naturally constitutes a leveled multi-key FHE scheme in the same setting. Comparative analysis results show that the proposed protocol is superior to the existing schemes in terms of overall performance.

secure multi-party computation; multi-key fully-homomorphic encryption; key homomorphism; threshold decryption; GSW13

2016- 06- 05

国家自然科学基金资助项目(61262008,61462017)；广西密码学与信息安全重点实验室开放课题(GCIS201622)

*Foundationitems: Supported by the National Natural Science Foundation of China (61262008，61462017)

王会勇(1977-),男,博士,讲师，主要从事网络信息安全研究.E-mail:why608@163.com

1000- 565X(2017)07- 0069- 08

TP 309.7

10.3969/j.issn.1000-565X.2017.07.010