考虑机电耦合的电动轮系统纵向振动特性建模及验证
2017-12-15左曙光李多强邓文哲吴旭东
左曙光,李多强,毛 钰,邓文哲,吴旭东
考虑机电耦合的电动轮系统纵向振动特性建模及验证
左曙光,李多强,毛 钰,邓文哲,吴旭东※
(同济大学新能源汽车工程中心,上海 201804)
为了研究机电耦合对电动轮系统的纵向振动特性的影响,该文首先建立了电动轮纵扭耦合动力学模型,基于该模型分析了考虑机电耦合前后电动轮系统模态特征的变化,并通过轮毂电机驱动电动轮系统的振动特性试验,验证了该动力学解析模型的准确性;其次分析了机电耦合对电动轮系统纵向振动的影响,指出转矩波动引起定转子发生相对运动,导致电机发生偏心,从而产生不平衡磁拉力。不平衡磁拉力的作用导致非簧载部分纵向振动出现不同程度的恶化,当轴承刚度为12.5 MN/m时,在定子纵向平移模态频率下电机的定转子、轮胎纵向振动加速度分别恶化113.35%、105.69%、27.15%,影响其使用寿命和结构安全,而对于簧载部分纵向振动的影响较小。
车辆;振动;模型;机电耦合;电动轮;转矩波动;不平衡磁拉力
0 引 言
近年来,随着电动汽车的兴起,其关键部件电动轮系统成为开发研究的核心[1-3]。针对电动轮一悬架系统振动特性,目前的研究尚不充分,文献[4-6]考虑了轮毂电机与轮胎之间的耦合动力学关系但是分析对象是路面激励下考虑增加电机质量对垂向振动的影响,分析频率较低,采用的轮胎模型也较为简单,均不能反映轮毂电机高频转矩激励下的电动轮振动特性。
电动轮系统中的轮毂电机受到高频转矩波动的作用,导致纵向振动上的问题相对于垂向更显著[7]。张立军等[8]基于轮毂电机-轮胎总成非线性动力学模型分析了轮毂电机转矩波动引起的轮胎纵向接地力的阶次振荡。毛钰等[7]通过台架试验揭示了电动轮系统纵向振动的阶次特征和高频特性,基于刚性环理论的建立了电动轮系统的动力学模型,并进行了模态分析,通过理论解释了电动轮高频振动现象。上述文献在分析电动轮系统的纵向振动时,将电机作为一个整体进行建模,然而实际运行过程中电动轮系统是一个复杂的机电耦合系统。
电动轮系统的纵向振动引起轮毂电机的定转子发生相对运动,导致径向气隙不再均匀,进而产生不平衡磁拉力(unbalanced magnetic pull,UMP)直接作用于在电动轮系统电机的定转子上,这将导致电动轮系统的纵向振动特性发生改变。此外不平衡磁拉力会进一步加剧径向气隙不均匀性,因此考虑机电耦合产生的不平衡磁拉力对电动轮系统的振动影响尤为重要。
Tan 等[9-10]分析了由轮毂电机产生不平衡磁拉力对电动汽车的横向和垂向耦合动力学的影响,指出不平衡磁拉力不同程度恶化垂向和横向的振动,在设计轮毂电机驱动电动汽车时,不平衡磁拉力必须作为一个重要的考虑因素;Wang等[11-12]分析了开关磁阻电机(switched reluctance motor,SRM)不平衡磁拉力与路面激励相耦合下的车辆的垂向振动,指出SRM不平衡磁拉力与路面激励和开关磁阻电机气隙偏心高度耦合,这种耦合效应恶化了车辆垂向振动。文献[9-12]指出不平衡磁拉力对于电动轮系统的振动具有重要影响,然而他们都是针对机电耦合产生的不平衡磁拉力对垂向和横向振动特性的研究,鲜有学者考虑不平衡磁拉力对系统纵向振动特性的影响。因此研究考虑机电耦合产生的不平衡磁拉力对于电动轮系统的纵向振动的影响是十分必要的。
为研究机电耦合产生不平衡磁拉力对电动轮系统的纵向振动特性的影响,本文首先建立了电动轮纵扭耦合动力学模型,基于该模型分析了考虑机电耦合前后电动轮系统模态特征的变化,并通过轮毂电机驱动电动轮系统的振动特性试验,验证了该动力学解析模型的准确性;随后基于建立的动力学模型分析了机电耦合产生的不平衡磁拉力对电动轮系统纵向振动的影响。
1 考虑机电耦合的电动轮系统纵向动力学建模及模态分析
1.1 电动轮系统纵向动力学建模及模态分析
由前期研究可知[13]转矩波动会通过轮胎与路面的附着作用引起纵向接地力波动进而激发电动轮纵向振动,即电动轮在电机转矩波动激励下主要表现为扭转和纵向振动,又因为电机转矩波动具有明显的阶次特性[14-15]。因此为了能够反映轮毂电机高频转矩波动激励下的电动轮振动特性,建立电动轮系统纵扭耦合动力学模型如图1所示。轮胎和电机转子通过胎侧连接,胎侧等效为扭转刚度和纵向平移刚度;电机定子经悬架摆臂及衬套与车身在纵向连接;电机定子与转子通过轴承连接;轮胎扭转自由度和纵向平移自由度通过考虑轮胎松弛特性的瞬态刷子模型实现耦合。
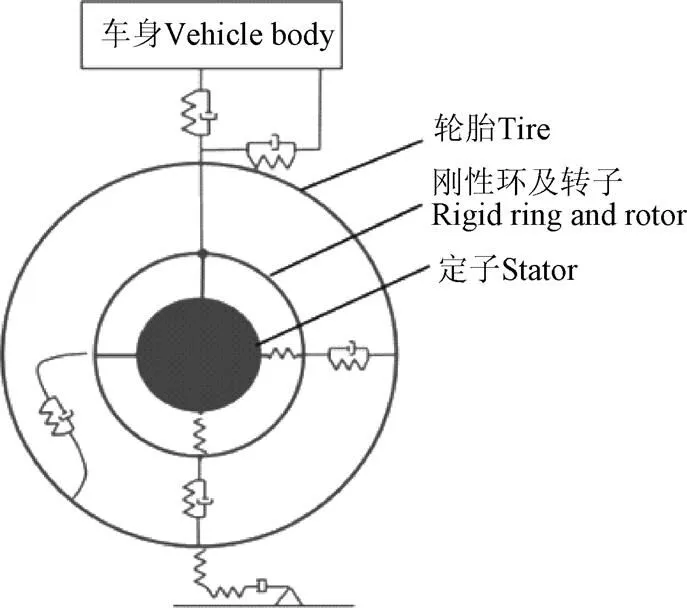
图1 电动轮系统纵扭耦合动力学模型
现有的文献在分析电动轮系统的纵向振动时时通常将电机的定转子视为整体[16-18]。而实际运行过程中电动轮系统是一个复杂的机电耦合系统。为了考虑电动轮系统的机电耦合特性,首先需要建立考虑定转子分开的电动轮纵向动力学方程,如式(1)所示。
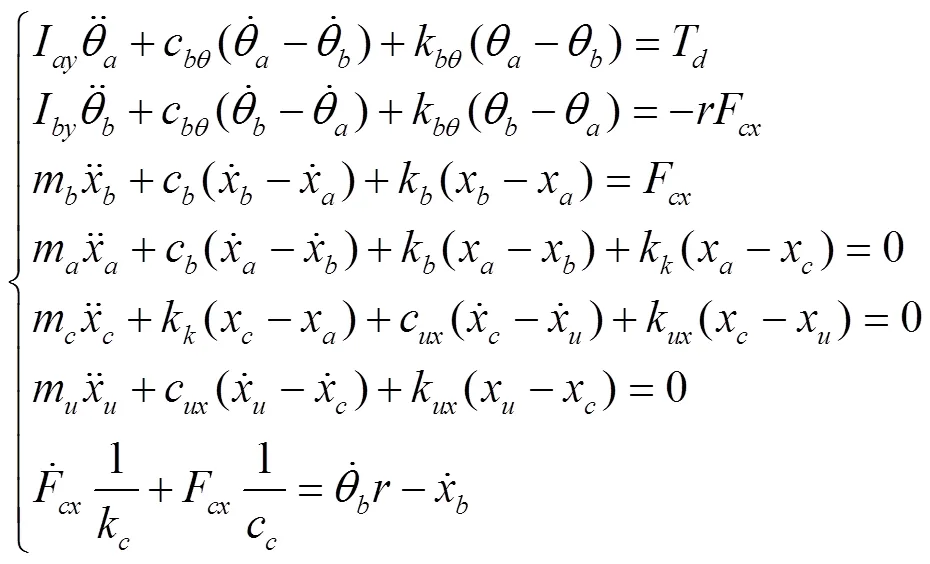
式中x、x、x为轮胎、轮辋/电机转子和电机定子纵向位移,m;θ、θ为电机转子和轮胎旋转角,rad;F为轮胎纵向力,N。电动轮模型参数如表1所示。
上述模型忽视了机电耦合产生的不平衡磁拉力。考虑机电耦合后,电动轮系统的纵向振动引起轮毂电机的定转子发生相对运动,导致径向气隙不再均匀,进而产生不平衡磁拉力直接作用于在电动轮系统电机的定转子上,导致电动轮系统的纵向动力学模型发生了变化。图2为轮毂电机纵向偏心的示意图。
因为铁芯材料的磁导率远远大于空气的磁导率,磁力线进出定子、转子铁芯时基本垂直于铁芯表面。因此对本文研究的径向电机,气隙磁通密度的切向分量远远小于径向分量,可以忽略不计。所以根据麦克斯韦张量方程,切向的电磁力f为0,径向电磁力f可近似表示为
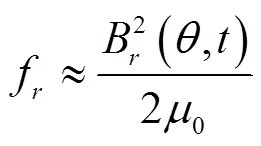
式中B(,)为电机的径向磁密,T;0为真空磁导率。
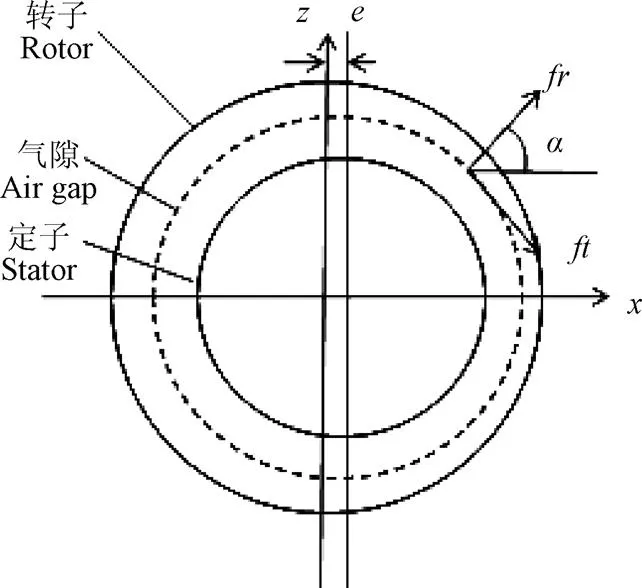
注:x、z表示坐标轴;e表示电机的偏心量,mm;α表示径向电磁力与x轴的夹角,rad。
将径向电磁力沿圆周积分后并化简得到总的不平衡磁拉力UMP为

式中l为电机轴向长度,m;为电机气隙半径,m。
该电动轮系统采用的轮毂电机为分数槽集中绕组的外转子永磁同步电机,其参数如表2所示。图3为有限元建立有限元模型仿真得出的不平衡磁拉力与纵向偏心间关系,可知该不平衡的磁拉力与偏心量的大小成正比,而偏心量等于定转子的相对位移。则不平衡磁拉力可以表示为

式中k为电磁刚度,其大小等于曲线的斜率3.25 MN/m。

表2 永磁同步电机参数
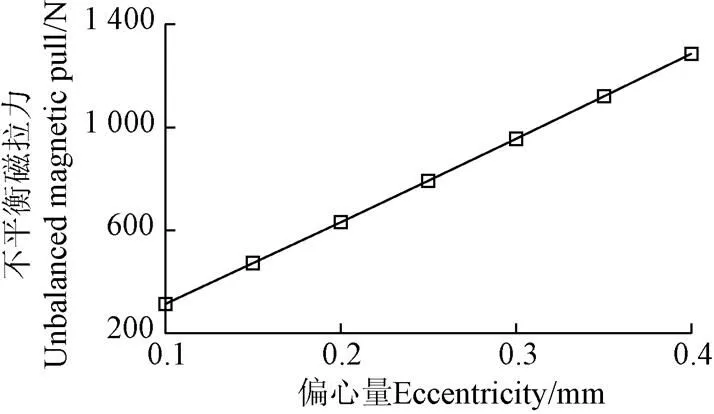
图3 不平衡磁拉力与纵向偏心的关系
在实际中,不平衡磁拉力以一对相互作用力的形式,作用在电机的定转子上。此时考虑机电耦合产生的不平衡磁拉力后的电动轮纵向动力学方程如式(5)所示。

将式(1)和(5)表达成状态空间形式,根据线性系统理论求解出特征值与特征向量,在Matlab中通过振型归一化和无量纲化判断振型特征,分析结果如表3所示。

表3 电动轮模态参数
由表3可以看出,考虑机电耦合产生的不平衡磁拉力后,电动轮系统的各阶振型特征不变,但表现为定子的纵向平移的第五阶模态频率下降,由130.08降为112.34 Hz,其余阶模态频率几乎保持不变。这是因为不平衡磁拉力对于电机的定转子来说是外力,对于车身和轮胎是内力,所以系统的第五阶模态即振型为定子的纵向平移对应的模态频率受影响较大。
1.2 试验验证
为验证轮毂电机驱动电动汽车在驱动电机转矩波动激励下振动特性研究所建解析模型的准确性,本文通过某电动汽车电动轮系统的台架试验进行了验证。该四分之一电动轮系统采用双横臂悬架,安装在课题组开发的悬架试验台架上[19],轮胎直接与转鼓相接触,如图4所示。试验过程中轮胎由轮毂电机驱动,并通过转鼓施加负载以模拟车辆行驶过程中的阻力。通过加速度传感器采集了轮胎的纵向加速度信号。

图4 电动轮台架试验布置
试验工况设定为电机驱动转矩60 N·m,转速在30 s内由0加速到300 r/min。图5为试验获取的轮胎纵向加速度的时频图。
由图5可知,轮胎振动表现出阶次特征,主要阶次为1、5、5.5、6、6.5等,其中6阶振动最为明显,主要是由于电机的6阶转矩波动引起的。汽车从0起步加速到30 km/h时,电机转速从0加速到300 r/min,转矩波动频率可以达到360 Hz,因此本文的激励频率超过了100 Hz。这里涉及的阶次均相对于电流基频(转频与极对数的乘积),6阶表示电流基频的6倍频。另外从图5中可以看出在整个频段内轮胎的纵向振动存在着3个明显的共振区。提取轮胎纵向振动时频图中6阶振动切片如图6所示,3个共振区对应的频率分别位于48、94及141 Hz,这与表3中通过解析模型计算获取的模态频率相接近,从而验证了电动轮系统纵向动力学解析模型的准确性。同时可以看出,轮胎振动显著的频段为0~150 Hz,高于150 Hz的频段内振动幅值较小。因此本文分析的主要频率在150 Hz以内,而所建解析模型能够反映该频段的振动特性,可进一步用于电动轮系统的纵向动力学分析。
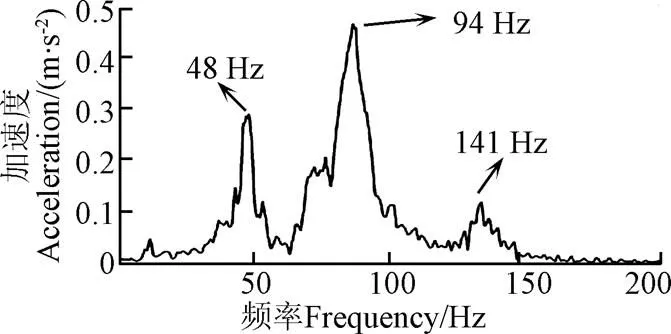
图6 轮胎6阶纵向振动加速度
2 考虑机电耦合的电动轮系统纵向振动特性分析
2.1 电动轮系统机电耦合下不平衡磁拉力
分析振动来源[20]可知,转矩波动具有明显的阶次特征。转矩波动包括电机绕组不通电时永磁体和定子开槽相互作用产生的齿槽转矩和由永磁体和电枢反应磁场共同作用产生的电磁转矩脉动两部分。由文献[21-23]可知齿槽转矩的脉动频率为电机极槽最小公倍数的整数倍转频,由文献[24-26]可知电磁转矩脉动频率为6(为极对数)的整数倍转频。对于本文研究的24极27槽电机来说,其齿槽转矩的频率为216f,电磁转矩波动的频率为72f(f为电机的转频、为整数)。由文献[14]可知,转矩波动的基波对纵向振动特性的影响较大,所以为便于后续分析考虑机电耦合产生的不平衡磁拉力对电动轮系统纵向振动的影响,电动轮系统输入激励为转矩

为反映电动轮系统在整个转速范围内的动力学特性,分析轮毂电机加速工况下气隙的变化如图7a所示,图7b展示了由气隙变化产生的不平衡磁拉力。
由图7可知,转矩波动引起定转子发生相对运动,即气隙发生变化,导致电机发生偏心,产生不平衡磁拉力。当轴承的刚度为12.5 MN/m时,轮毂电机气隙最大偏心率达3.5%,不平衡磁拉力的最大值达119 N。对比分析发现不平衡磁拉力亦会加剧气隙的变化,二者存在很强的正相关性;齿槽转矩与不平衡磁拉力共同作用是气隙在低频段变化的主要原因,高频段则主要受电枢与永磁体磁场相互作用产生的转矩波动与不平衡磁拉力的共同影响。

图7 轮毂驱动电机的气隙变化及不平衡磁拉力
2.2 不平衡磁拉力对电动轮系统纵向振动特性影响
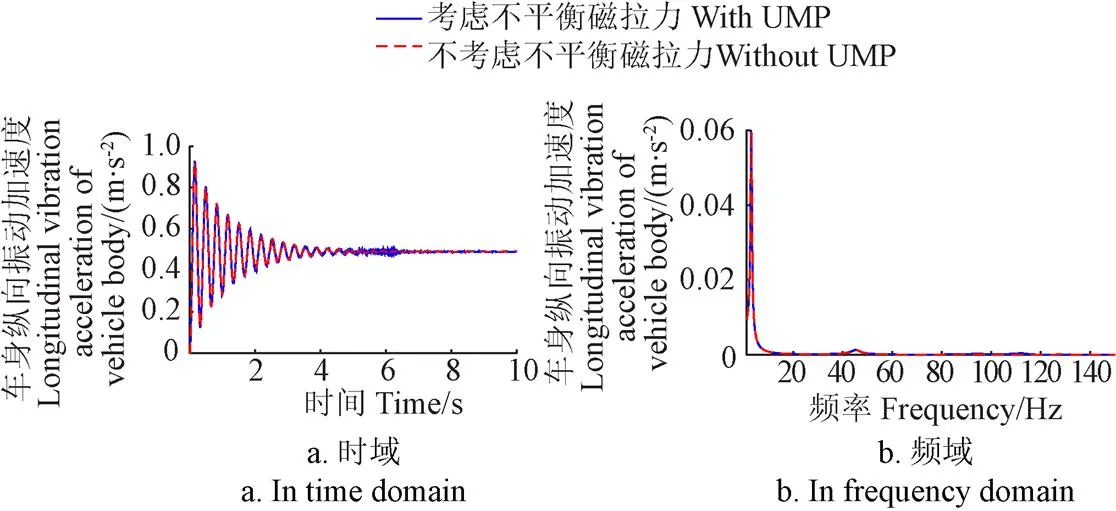
人体对低频的纵向振动较为敏感,因此车身在2~3 Hz附近的纵向振动将显著影响轮毂电机驱动电动汽车的乘坐舒适性。对于电动轮系统,由于转矩波动的作用,轮胎滑移率会在中高频附近出现显著波动,中频波动难以准确测量或估计,进而使滑移率的辨识的存在误差,对车辆纵向动力学控制(如ABS,TCS等)有显著影响[27-29]。在电机的诸多失效形式中,电机长时间工作在中高频激励下引起的结构件(诸如轴承、定转子等)疲劳破坏是主要贡献之一[30]。为分析考虑机电耦合产生不平衡磁拉力对车辆舒适性、电机结构稳定性、纵向滑移率辨识等影响,仿真得出加速工况下车身、电机定转子和轮胎纵向加速度时域图,进而通过短时傅里叶变换得到对应的频域结果如图8至图11所示。
注:图中两条曲线近似重合。
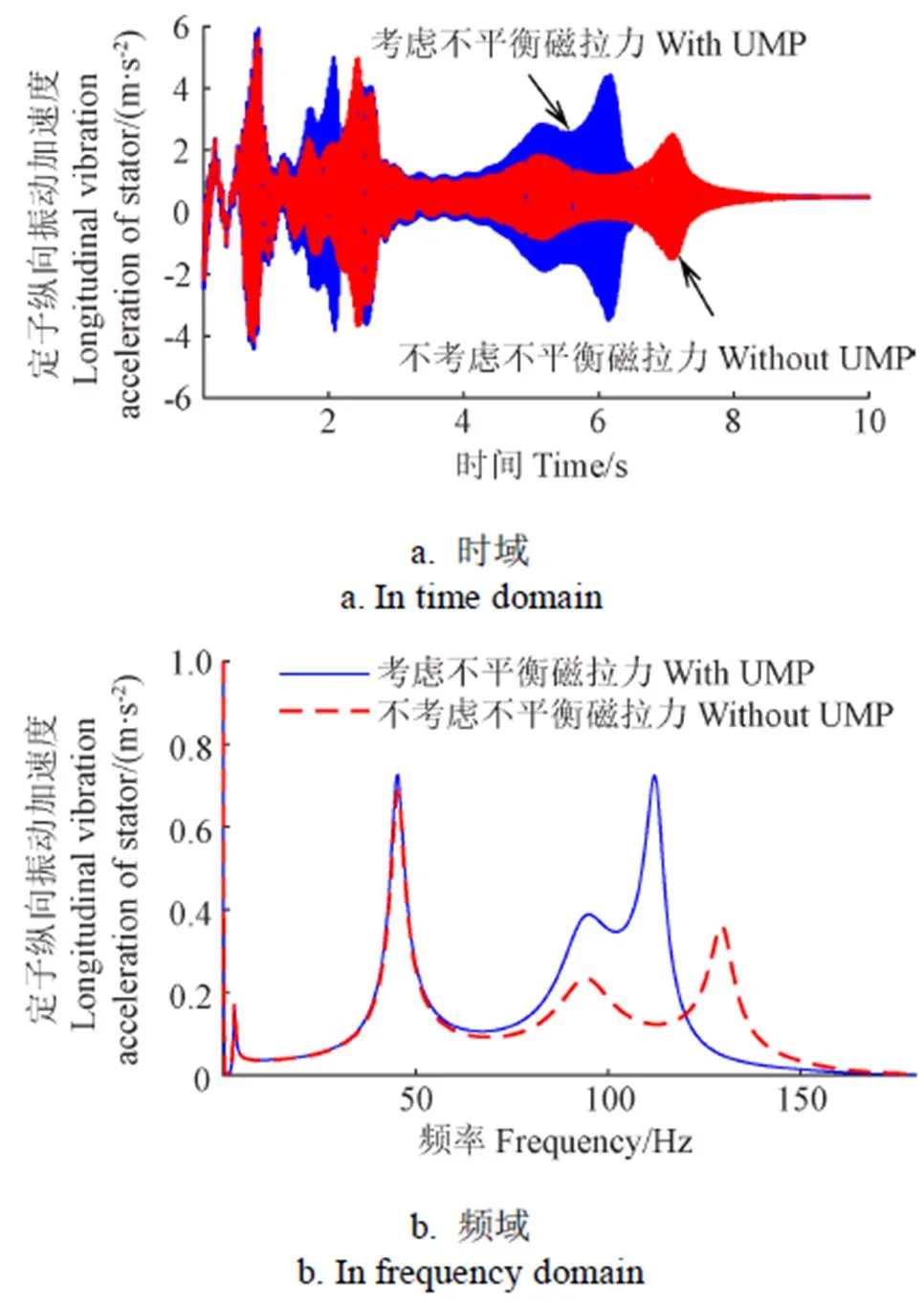
图9 定子纵向振动加速度
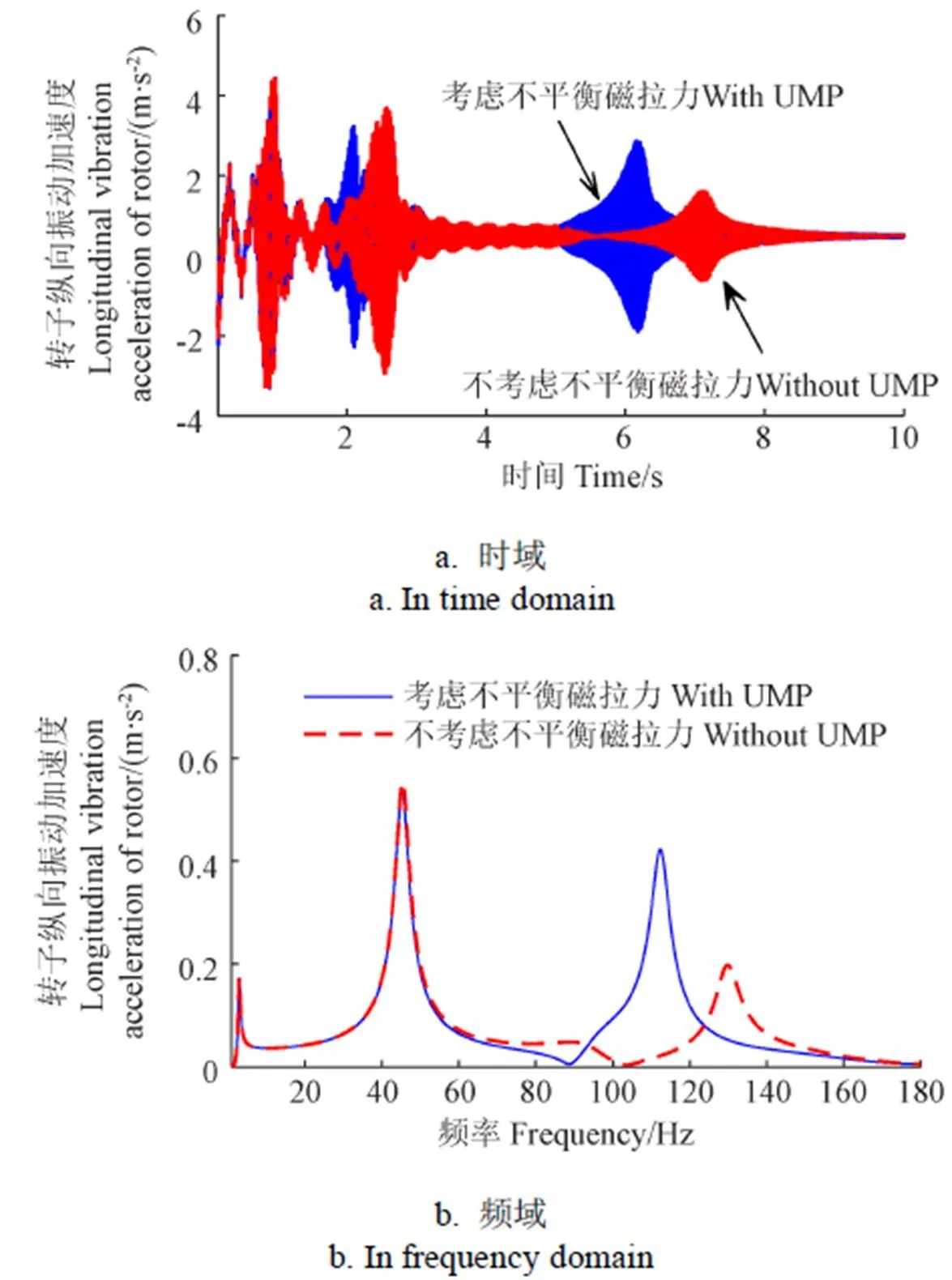
图10 转子纵向振动加速度
由图8到图11可知:考虑机电耦合产生的不平衡磁拉力对系统的第五阶模态影响较大,表现为频率下降,且电机定转子的振动幅值在此阶模态处增大许多,即电机及定转子的纵向振动由第五阶贡献增多,因为电动轮系统的第五阶模态表现为定子的纵向平移。而机电耦合产生的不平衡磁拉力对于车身及轮胎的纵向振动影响相对较小。为定量分析不平衡磁拉力对车身及簧下部件纵向振动的影响,分别取=108.4、93.62 r/min,此时转矩波动频率分别与考虑机电耦合产生不平衡磁拉力前后第五阶所对应的模态一致,仿真获取各响应量纵向振动加速度均方根值如表4所示。
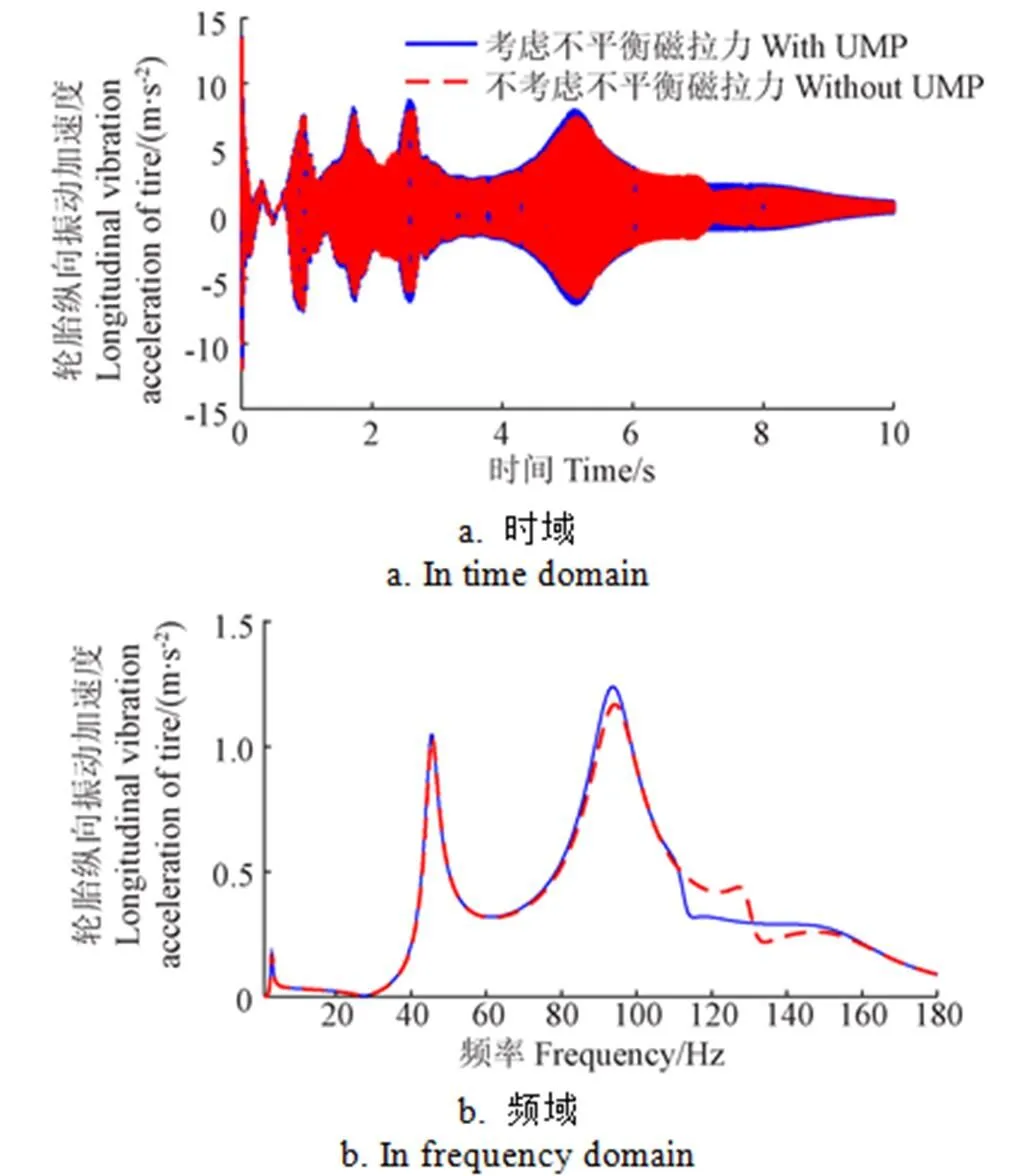
注:图11a中,仅在1.7、2.6、5.1 s时,考虑不平衡磁拉力略大于不考虑不平衡磁拉力的轮胎纵向振动加速度;其余时间段轮胎纵向振动加速度几乎相等。
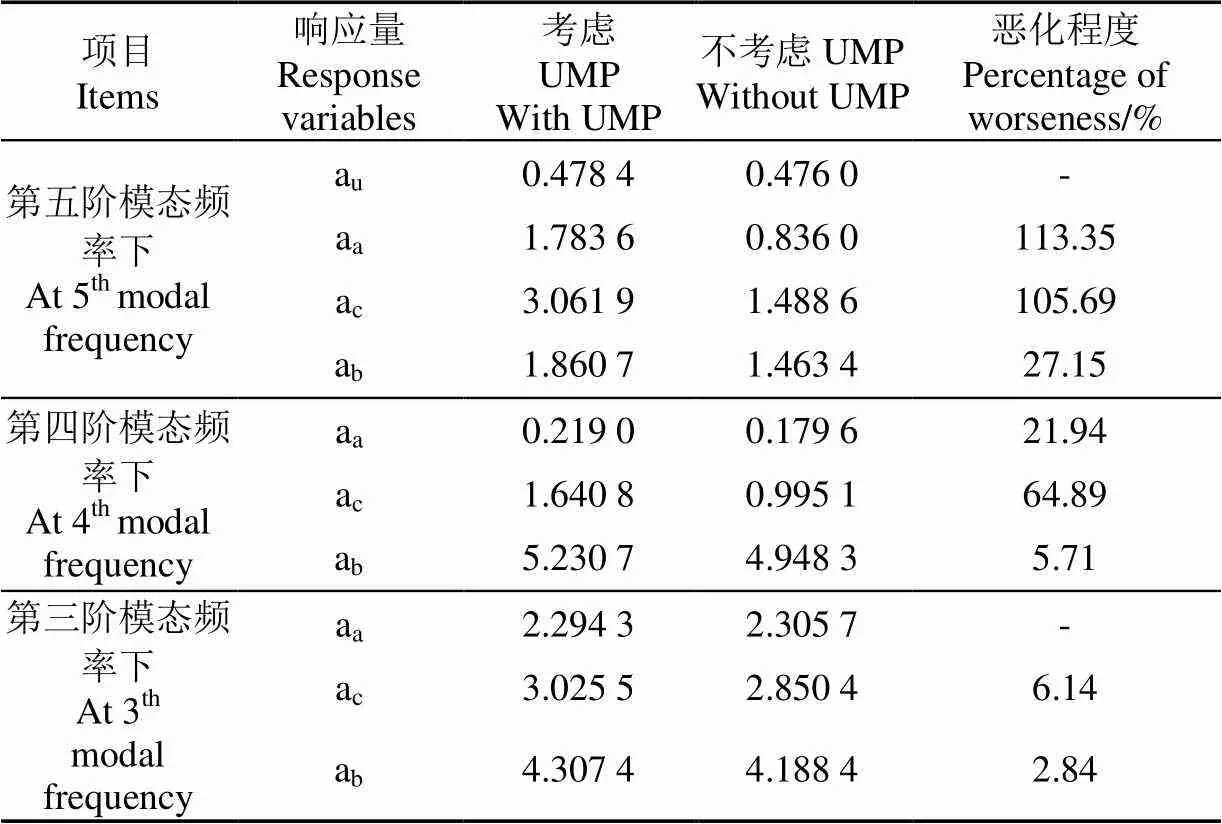
表4 纵向振动加速度恶化程度
注:a表示车身纵向振动加速度,m·s-2;a表示转子纵向振动加速度,m·s-2;a表示定子纵向振动加速度,m·s-2;a表示轮胎纵向振动加速度,m·s-2。
Note:aindicates longitudinal vibration acceleration of vehicle body, m·s-2;aindicates longitudinal vibration acceleration of rotor, m·s-2;aindicates longitudinal vibration acceleration of stator, m·s-2; aindicates longitudinal vibration acceleration of tire, m·s-2.
由表4可知,机电耦合产生的不平衡磁拉力使电机的定转子、轮胎在第五阶模态频率处的纵向振动加速度都不同程度的增大,分别增加113.35%、105.69%、27.15%,对于车身纵向振动加速度几乎无影响。
在电动轮系统中,由于轮毂电机驱动的轮胎/车轮等动力学结构存在柔性,反作用于电机的负载转矩在45.41及94.28 Hz处使定转子及轮胎纵向振动比较显著,且电机长时间工作下的中高频激励将引起结构件的疲劳破坏,故分析系统在第三、四阶模态下,即转速=37.85、78.75 r/min时,机电耦合产生的不平衡磁拉力对簧下部件纵向振动的影响。机电耦合产生的不平衡磁拉力使电机的定子、轮胎纵向振动加速度在第三阶模态频率处分别增加6.14%、2.84%,对转子纵向振动加速度几乎无影响;在第四阶模态频率处使电机的转子、定子、轮胎纵向振动加速度分别增加21.94%、64.89%、5.71%。
因为本文主要考虑机电耦合对电动轮系统的纵向振动特性影响,由模态频率分析发现只有在定子的纵向平移的振动特征的模态频率有所下降。这是因为不平衡磁拉力对于电机的定转子来说是外力,直接作用在定转子上,对于车身和轮胎是内力,所以振型为定子的纵向平移对应的模态频率变化较大。在电机结构中,定转子只由轴承这一物理结构直接相连,所以模型参数中只有轴承刚度的改变对于考虑机电耦合产生的不平衡磁拉力影响较大,进而影响该电动轮系统的纵向振动特性。由文献[31]可知,轴承的安装刚度一般在12.5~22.5 MN/m,因此在不同轴承刚度下,仿真获取了激励频率分别为考虑机电耦合前后定子纵向平移模态的频率时簧下质量纵向振动加速度的均方根值,分析了不同刚度下簧下质量纵向振动的恶化程度,结果如图12所示。
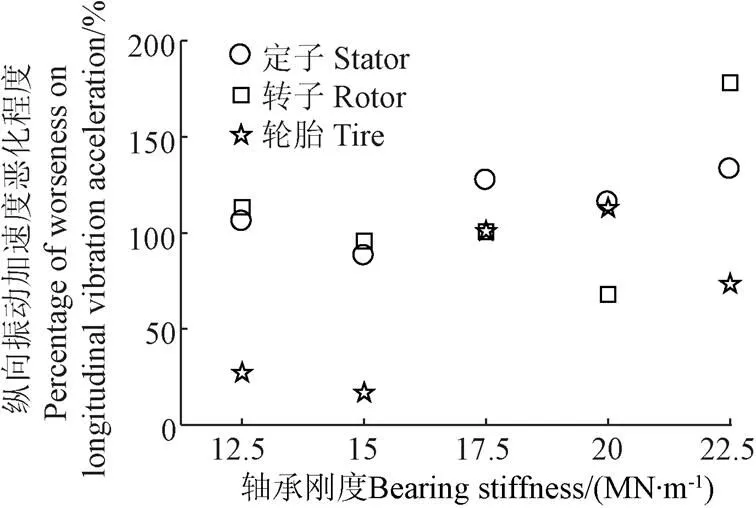
图12 不同轴承刚度下簧下质量纵向振动加速度恶化情况
由图12可知在实际轴承的安装刚度范围内,考虑机电耦合后,簧下质量的纵向振动加速度出现不同程度的恶化,影响其使用寿命和结构安全。
3 结 论
本文建立了考虑机电耦合产生不平衡磁拉力的电动轮纵向动力学模型,并分析了考虑前后模态特征的变化;研究了在转矩波动输入下,机电耦合产生不平衡磁拉力对电动轮系统纵向振动特性的影响,得出以下结论:
1)基于电动轮纵扭耦合动力学模型,分析考虑机电耦合后,电动轮系统各阶模态的变化规律:表现为定子的纵向平移的振动特征的模态频率下降,其余阶模态频率几乎保持不变。
2)当轴承刚度为12.5 MN/m时,机电耦合产生的不平衡磁拉力使定子纵向平移模态频率下电机的定转子、轮胎纵向振动加速度分别恶化113.35%、105.69%、27.15%;在其余轴承刚度下,机电耦合导致簧下质量的纵向振动亦出现了较大程度的恶化,使其控制难度加大,并严重影响其使用寿命和结构安全。因此在电动汽车的开发中考虑机电耦合产生的不平衡磁拉力很有必要。
[1] 电动汽车总体专项组. “十五”国家高技术研究发展计划(863计划)电动汽车重大专项进展[J]. 汽车工程,2003,25(6):533.
The Special Professioml Group of Electric Vehicle. National high-tech research and development program for tenth “Five-year Plan”(863 Torch Program): Significant progress of electric vehicle[J]. Automotive Engineering, 2003, 25(6): 533. (in Chinese with English abstract)
[2] Li X H, Qian H. The present status and future trends of in-wheel motors for electric vehicles[J]. Advanced Materials Research, 2012, 433: 6943-6950.
[3] Chen Y, Wang J M. Design and evaluation on electric differentials for overactuated electric ground vehicles with four independent in-wheel motors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1535-1542.
[4] Nagaya, Wakao Y, Abe A. Development of an in-wheel drive with advanced dynamic-damper mechanism[J]. Jsae Review, 2003, 24(4): 477-481.
[5] Jin L, Song C, Wang Q. Evaluation of influence of motorized wheels on contact force and comfort for electric vehicle[J]. Journal of Computers, 2011, 6(3): 497-505.
[6] 梁锐,余卓平,宁国宝. 基于吸振原理的轮边驱动电动车垂向振动负效应的抑制[J]. 机械设计,2008,25(1):28-30.
Liang Rui, Yu Zhuoping, Ning Guobao. Restraint of negative effect on vertical vibration of wheel rim driven motor vehicle based on shake absorption principle[J].Journal of Machine Design, 2008, 25(1): 28-30. (in Chinese with English abstract)
[7] 毛钰,左曙光,林福. 转矩波动下电动轮纵向阶次振动特性试验及理论分析[J].同济大学学报:自然科学版,2016,44(11):1735-1742.
Mao Yu, Zuo Shuguang, Lin Fu. Experimental and theoretical analysis of horizontal order vibration characteristics of electric wheel under torque ripple[J]. Journal of Tongji University: Natural Science, 2016, 44(11): 1735-1742. (in Chinese with English abstract)
[8] 张立军,钱敏,余卓平. 轮毂电机-轮胎总成非线性动力学特性仿真分析[C]//第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛优秀论文集(下册). 北京:电子工业出版社,2009:162-168.
[9] Tan Di, Lu Chao. The Influence of the magnetic force generated by the in-wheel motor on the vertical and lateral coupling dynamics of electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4655-4668.
[10] Luo Yutao, Tan Di. Study on the dynamics of the in-wheel motor system[J]. IEEE Transactions on Vehicular Technolog, 2012 , 61(8): 3510-3518.
[11] Wang Y, Li P, Ren G. Electric vehicles with in-wheel switched reluctance motors: Coupling effects between road excitation and the unbalanced radial force[J]. Journal of Sound & Vibration, 2016, 372: 69-81.
[12] Wang Y Y, Li N, Sun W, et al. Effect of the unbalanced vertical force of a switched reluctance motor on the stability and the comfort of an in-wheel motor electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering, 2015, 229(12): 1569-1584.
[13] 左曙光,段向雷,吴旭东. 电动轮刚性环耦合特性模型建模与分析[J]. 同济大学学报:自然科学版,2014,42(10):1578-1585.
Zuo Shuguang, Duan Xianglei, Wu Xudong. Modeling and analysis of rigid ring coupling model of electric wheel[J]. Journal of Tongji University: Natural Science, 2014, 42(10): 1578-1585. (in Chinese with English abstract)
[14] Islam M S, Islam R, Sebastian T. Experimental verification of design techniques of permanent-magnet synchronous motors for low-torque-ripple applications[J]. IEEE Transactions on Industry Applications, 2009, 47(1): 88-95.
[15] 林福,左曙光,吴旭东,等. 基于阶次分析的永磁同步电机噪声源识别[J]. 农业工程学报,2016,32(17):69-76.
Lin Fu, Zuo Shuguang, Wu Xudong, et al. Noise source recognition of permanent magnet synchronous motor based on order analysis[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2016, 32(17): 69-76. (in Chinese with English abstract)
[16] 毛钰,左曙光,林福. 转矩波动下电动轮系统机电耦合振动特性[J]. 吉林大学学报:工学版,2017,47(3):908-916.
Mao Yu, Zuo Shuguang, Lin Fu. Electromechanical coupled vibration characteristics of electric wheel under torque ripple[J]. Journal of Jilin University: Engineering and Technology Edition, 2017, 47(3): 908-916. (in Chinese with English abstract)
[17] Mao Yu, Zuo Shuguang, Wu Xudong. Longitudinal vibration analysis of electric wheel system in starting condition[J]. SAE International Journal of Vehicle Dynamics, Stability, and NVH, 2017, 1(2): 156-164.
[18] Mao Yu, Zuo Shuguang, Wu Xudong, et al. High frequency vibration characteristics of electric wheel system under in-wheel motor torque ripple[J]. Journal of Sound and Vibration, 2017, 400: 442-456.
[19] 同济大学. 一种可调式电动轮悬架系统振动噪声测试台: 201310125584. 0[P]. 2013-08-07.
[20] Zuo Shuguang, Duan Xianglei, Wu Xudong. Vibration test analysis of an electric wheel-suspension system on a test bed[J]. Journal of Vibration and Shock, 2014, 33(12): 165-187.
[21] Ge X, Zhu Z Q, Kemp G, et al. Optimal step-skew methods for cogging torque reduction accounting for three- dimensional effect of interior permanent magnet machines[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 222-232.
[22] Shin K H, Park H I, Cho H W, et al. Analytical calculation and experimental verification of cogging torque and optimal point in permanent magnet synchronous motors[J]. IEEE Transactions on Magnetics, 2017, 53(6): 1-4.
[23] Li Yanxin, Lu Qinfen, Zhu J Q, et al.Superposition method for cogging torque prediction in permanent magnet machines with rotor eccentricity[J]. IEEE Transactions on Magnetics, 2016, 52(6): 1-10.
[24] 王斯博,赵慧超,李志宇,等. 电动车永磁同步电机转矩波动分析及测试[J]. 电机与控制学报,2015,19(9):95-102.
Wang Sibo, Zhao Huichao, Li Zhiyu, et al. Analysis and test for torque ripple of permanent magnet synchronous motor for electric vehicle[J]. Electric Machines and Control, 2015, 19(9): 95-102. (in Chinese with English abstract)
[25] Farshadnia M, Cheema M A M, Dutta R, et al. Detailed analytical modelling of fractional-slot concentrated-wound interior permanent magnet machines for prediction of torque ripple[J]. IEEE Transactions on Industry Applications, 2017, 53(6): 5272-5283.
[26] Lai C, Feng G, Iyer L V, et al. Genetic algorithm based current optimization for torque ripple reduction of interior PMSMs[J].IEEE Transactions on Industry Applications, 2017, 53(5): 4493-4503.
[27] Song Ziyou, Li Jianqiu, Wei Yintao, et al. Interaction of in-wheel permanent magnet synchronous motor with tire dynamics[J]. Chinese Journal of Mechanical Engineering. 2015, 28(3): 470-478.
[28] Li Jianqiu, Song Ziyou, Wei Yintao, et al. Influence of tire dynamics on slip ratio estimation of independent driving wheel system[J]. Chinese Journal of Mechanical Engineering. 2015, 27(6): 1203-1209.
[29] 李波,赵又群,臧利国,等. 基于复合滑移理论的轮胎抓地状态建模与验证[J]. 农业工程学报,2014,30(16):68-74.
Li Bo, Zhao Youqun, Zang Liguo, et al. Construction and verification of tire grip state based on combined-slip theory[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2014, 30(16): 68-74. (in Chinese with English abstract)
[30] Matej B, Gorazd G, Damijian M, et al. Mechanical failure mode causes of in-wheel motors[J]. Journal of Mechanical Engineering, 2015, 61(1): 74-85.
[31] 史魁,岳永坚. 电动机转子深沟球轴承刚度的测试[J]. 现代制造工程,2013(12):77-80.
Shi Kui, Yue Yongjian. Stiffness measurement of deep- groove ball bearing using in electromotor rotor[J]. Modern Manufacturing Engineering, 2013(12): 77-80. (in Chinese with English abstract)
左曙光,李多强,毛 钰,邓文哲,吴旭东. 考虑机电耦合的电动轮系统纵向振动特性建模及验证[J]. 农业工程学报,2017,33(22):61-68. doi:10.11975/j.issn.1002-6819.2017.22.008 http://www.tcsae.org
Zuo Shuguang, Li Duoqiang, Mao Yu, Deng Wenzhe, Wu Xudong. Modeling and validation on longitudinal vibration characteristics of electric wheel system considering electromechanical coupling[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(22): 61-68. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.22.008 http://www.tcsae.org
Modeling and validation on longitudinal vibration characteristics of electric wheel system considering electromechanical coupling
Zuo Shuguang, Li Duoqiang, Mao Yu, Deng Wenzhe, Wu Xudong※
(201804,)
Recently, distributed-drive electric vehicle has become one of the development directions of future vehicle with the advantage of miniaturization and high performance. The electric wheel system is a key component of distributed-drive electric vehicle. The longitudinal dynamics of electric wheel system caused by torque ripple of the in-wheel motor is more significant than vertical. The existing studies on longitudinal vibration analysis of electric wheel system are always taking stator and rotor as a whole. Actually, the electric wheel is a complicated electromechanical coupling system. The longitudinal vibration of electric wheel system causes the relative displacement of rotor and stator, resulting in unbalanced magnetic pull (UMP) that acts on the surface of rotor and stator. The induced UMP by electromechanical coupling changes the characteristics of the longitudinal vibration and deteriorates the performance of the electric wheel system further. Therefore, it is important to consider the effects of UMP caused by electromechanical coupling on the longitudinal vibration of the electric wheel system. Longitudinal vibration characteristics of an electric wheel system considering electromechanical coupling was studied in this paper. Firstly, the electric wheel longitudinal-tensional coupling dynamic model was established, and the variation of the modal characteristics for the electric wheel system with and without electromechanical coupling was analyzed. It needs to indicate that the modal shapes of the electric wheel system are identical considering the UMP, but the fifth order modal frequency is decreased obviously. This mode was characterized as the longitudinal translation of the stator. The accuracy of the analytical dynamic model was verified through vibration test of a one-quarter electric wheel system. The electric wheel system adopted a double-wishbone suspension and was installed on the experiment bench developed by the research group. During the test, the tire was driven by the in-wheel motor and directly contacted with the drum. The load on the tire was exerted by the drum to simulate the resistance in the course of vehicle running. The longitudinal acceleration of tire was measured by an acceleration sensor. Time frequency map of the tire longitudinal vibration was then extracted. Three main resonance regions could be found near 48, 94 and 141 Hz, which were consistent with the modal frequencies obtained by the established analytical model. This verified the accuracy of the analytical model on longitudinal dynamics of electric wheel system. When longitudinal vibration frequency of the vehicle driven by in-wheel motor was near 2-3 Hz, it significantly affected the riding comfort as people are sensitive to low-frequency longitudinal vibration. While the high frequency longitudinal vibration is not favorable to the motor. Finally, the longitudinal vibration characteristic of the electric wheel system considering electromechanical coupling was studied. The time and frequency domain acceleration of vehicle body, stator, rotor and tire were obtained by simulation. It inferred from the quantitative analysis that torque ripple caused the relative displacement of stator and rotor, resulting in eccentric of the motor and UMP. The UMP is regarded as external force for the stator and rotor of the motor, while it is regarded as internal force for the vehicle body and tire. As a result, the unbalanced magnetic pull had little influence on the longitudinal vibration characteristic of sprung mass. However, it deteriorated the longitudinal vibration characteristic of unsprung mass sharply, which was harmful to the service life and structure safety. Therefore, it is necessary to consider the unbalanced magnetic pull caused by electromechanical coupling in the development of electric vehicle. This study provides guidance for the design of electric vehicles driven by in-wheel motor.
vehicles; vibrations; models; electromechanical coupling; electric wheel; torque ripple; unbalanced magnetic pull
10.11975/j.issn.1002-6819.2017.22.008
U461.1
A
1002-6819(2017)-22-0061-08
2017-06-23
2017-09-20
国家自然科学基金资助项目(51375343);上海市教委科研创新项目(15ZZ015)
左曙光,教授,博士生导师,研究方向为汽车系统动力学与控制。Email:sgzuo@tongji.edu.cn
吴旭东,助理教授,研究方向为汽车振动、噪声及系统动力学。Email:wuxudong@tongji.edu.cn
