差动轮系动态跟随性能研究

徐 琳 刘 凯 崔亚辉 孟培媛

西安理工大学机械与精密仪器工程学院，西安,710048

差动轮系动态跟随性能研究

徐 琳 刘 凯 崔亚辉 孟培媛

西安理工大学机械与精密仪器工程学院，西安,710048

以差动轮系为研究对象，分析了三个基本构件之间的转速、转矩以及功率关系，在此基础上提出了相应的灵敏度与贡献度概念并获得对应的表达式。进一步研究了灵敏度与贡献度的影响参数以及影响规律并展开了相关的对比实验。研究结果表明：转速灵敏度和转矩贡献度只与差动轮系特性参数相关；转速贡献度和功率贡献度由特性参数以及轮系转速匹配关系共同决定。灵敏度与贡献度反映了差动轮系在运动中的动态跟随性能，对差动轮系的选型与设计有参考作用。

差动轮系；灵敏度；贡献度；动态跟随性能

0 引言

差动轮系因体积小、传动比大、传动稳定、传动方式灵活以及效率高等优势而被广泛应用，是航空器、风力发电机、煤矿机械与汽车传动的重要组成部分[1-6]。

现有的差动轮系研究主要集中在轮系的运动学、静力学特性和动力学特性。在静力学分析方面，文献[7-9]对差动轮系的传动比与静力学特性进行了研究并加以试验验证;文献[2-5，10]对差动轮系组成的复合结构进行了运动学与静力学分析。以上文献主要研究差动轮系传动比在复合结构中带来的运动效果以及传动比变化产生的能量损失，并以此作为结构选型的依据。在动力学特性分析方面，国内外的研究人员分别考虑了轮系啮合刚度[11-13]、齿侧间隙[11，13]、轴承间隙[14]、齿间滑动摩擦[15]以及变载激励[16-17]等因素下的振动问题。这些研究的重要关注点在行星轮系的固有频率与振动模态，考察的是轮系在瞬态下的特性。

差动轮系在变速箱、分动箱和混合动力汽车等应用中，系统多处于不稳定状态，速度与载荷的变化迅速且复杂。如何快速有效地调整速度、转矩和功率,使得轮系能跟随工作情况的变化而正常运行也是设计选型中需要重点考虑的。本文就此问题提出了转速、转矩和功率三种特性的灵敏度及贡献度的概念。灵敏度反映的是轮系不同基本构件在运动过程中转速、转矩和功率三种特性的调整速度；贡献度反映的是不同基本构件在运动过程中这三种特性的调整效果。灵敏度与贡献度是差动轮系输入输出关系动态跟随性能的重要指标。

1 差动轮系运动学分析

图1所示为差动轮系的简化模型，图中X代表差动轮系，具有两个自由度，a、b、c为轮系结构的三个伸出端，称为三个基本构件。差动轮系通过a、b、c与外部机构连接，实现两个输入、一个输出(以下简称“两入一出”)或两个输出、一个输入(以下简称“一入两出”)的灵活应用。

图1 差动轮系的简化模型Fig.1 Simplified model of DGT

基于转化机构法，三个基本构件之间的转速关系满足Willis公式[18]：

(1)

(2)

因而，式(1)可以表示为

(3)

1.1 灵敏度分析

差动轮系的运动具有两个自由度，每个构件的转速皆受另两个构件转速的共同影响。在此，将任一个基本构件相对于另两个基本构件转速变化的灵敏性称为转速灵敏度，它反映了基本构件之间的速度跟随性的优劣，是机械传动的重要动态指标之一。

(4)

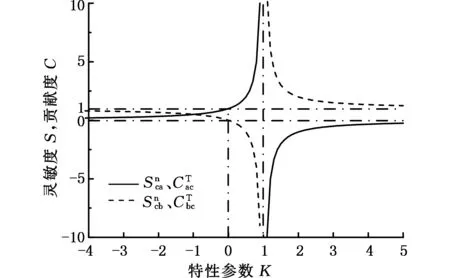
图2 转速灵敏度与转矩贡献度Fig.2 Speed sensitivity curves and torque contribution

当差动轮系基本构件a、构件b调速时，构件之间的转速变化量满足

(5)

1.2 贡献度分析

(6)

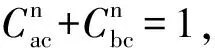
(7)

图3为构件a、构件b对构件c的转速贡献度随特性参数K变化的曲线，图3a为na/nb<0情况下的曲线，图3b为na/nb>0情况下的曲线。

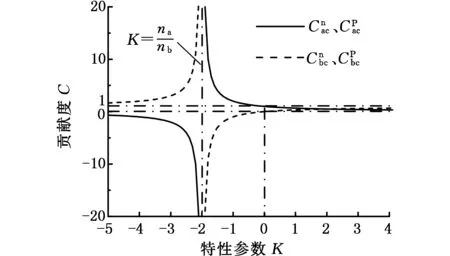
(a)na/nb<0

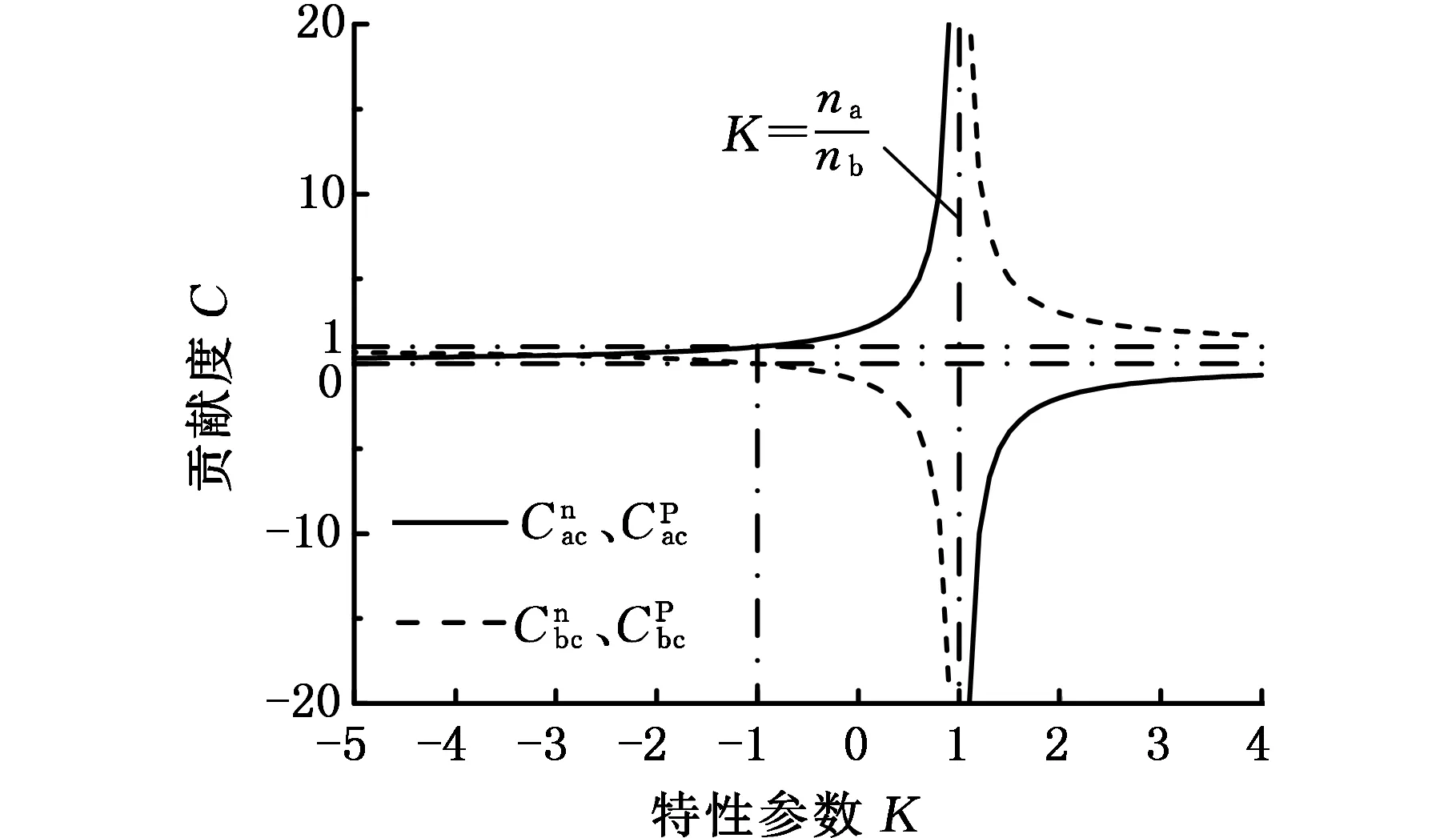
(b)na/nb>0图3 转速贡献度与功率贡献度Fig.3 Speed and power contribution curves

图3b与图3a曲线关于Y=0轴镜像，两者规律亦关于Y=0轴镜像。

2 差动轮系的力学分析

差动轮系的转矩关系满足下式：

Ta+Tb+Tc=0

(8)

Ta∶Tb∶Tc=1∶(-K)∶(K-1)

(9)

式中，Ti(i=a、b、c)为构件i的转矩。

式(8)、式(9)表明,差动轮系基本构件转矩和为零且三者之间满足的比例关系与特性参数K相关。

2.1 转矩灵敏度

若要将连接负载的构件c的带载能力提高到Tc+ΔTc(ΔTc为Tc的增加量)，有两种调节方式，分别是调节构件a与调节构件b的输入转矩。调节构件a的方式需要将Ta增大到Ta+ΔTa，根据式(8)、式(9)，调节后的转矩关系满足下式：

(Ta+ΔTa)∶(Tb+ΔTb)∶(Tc+ΔTc)=
1∶(-K)∶(K-1)

(10)

即

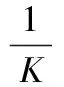
(11)

由式(9)有

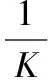
(12)

结合式(12)将式(11)中等式的每部分减去Ta，得到如下关系：

ΔTa∶ΔTb∶ΔTc=1∶(-K)∶(K-1)

(13)

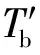
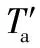
(14)

同理可得

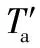
(15)

该结果说明对于差动轮系的转矩而言，无论哪种调节方式，轮系转矩的变化过程都一致，故而转矩灵敏度在差动轮系中不存在实际意义。此外构件之间的等比例增量说明构件之间不存在转矩的补偿关系，因此在设计中输入构件的转矩时应当分别按照各自转矩的最大需求设计，以满足工作负载要求。

2.2 转矩贡献度

(16)

对转矩贡献度的分析表明,差动轮系的三个基本构件的转矩必然有两个同向而与第三个反向。值得注意的是K=1以及K=0时的转矩贡献度情况。当某差动轮系的特性参数受无级调速控制变为1时，此时构件c的运动不确定且不受载，而构件a、构件b互为驱动负载。当K=0时，nc=na，Ta=-Tc，此时构件b的运动不确定且不受载，构件a、构件c互为驱动负载。

综上所述，差动轮系某一基本构件对另外两个基本构件的转矩灵敏度和转矩贡献度并不存在一致性。

3 差动轮系的功率分析

根据能量守恒定律，差动轮系的各基本构件a、构件b、构件c所传递的功率Pa、Pb、Pc满足如下关系：

Pa+Pb+Pc=0

(17)

根据基本构件之间的转速与转矩关系可得

(18)

3.1 功率灵敏度

(19)

由计算结果可知，在任意K的状况下，构件a、构件b的功率发生任何变化，都将在构件c上产生负变化，变化的大小与构件a、构件b初始变化的大小保持一致。

3.2 功率贡献度

(20)

假定构件c连接负载，Pc对应负载功率。当某基本构件功率贡献度的计算结果为负，即反映到构件c上为负功率时，该构件表现为与构件c同为负载，而功率贡献度为正的构件，则表现为动力源，起驱动作用。在图3a中，在K的整个负轴范围内，构件a、构件b中总有一个构件所贡献的功率反映到构件c上为负功率，而另一个构件所贡献的功率反映到构件c为正功率,即在该范围内，总有一个构件与构件c同为负载。在K的整个正轴范围内，构件a、构件b都为构件c贡献正功率。这说明在该K值范围内，构件a、构件b同为动力源，两者贡献功率的多少随K值而变。

图3b与图3a曲线关于Y轴镜像，曲线规律相反，说明当构件a、构件b有且只有一个转速反向时，功率贡献度关系将变为特性参数为-K时所对应功率贡献度关系。由此可见差动轮系三个基本构件功率的“两入一出”或“一入两出”不仅与特性参数K有关，还与转速匹配关系有关。结合转矩贡献度还可知功率概念的“两入一出”(或“一入两出”)与转矩概念的“两入一出”(或“一入两出”)并不一致。

此外，上述研究还说明差动轮系某一基本构件对另外两个基本构件的功率灵敏度和功率贡献度也不存在一致性。

4 实验验证

为了验证上文分析，选择转速灵敏度作为研究对象，在差动轮系实验台上进行了实验分析。图4所示为差动轮系实验台及其结构简图。

(a)实验台

(b)实验台结构简图图4 差动轮系实验台及其结构简图Fig.4 Picture and schematic of DGT test rig

实验台中，传动机构由差动轮系部分以及定轴轮系部分组成，由两个电机驱动，一个磁粉加载器作为负载输出，实现“两入一出”功能。在简图中，Z3、Z4、Z5、Z8、Z9、Z10、Z11组成差动轮系部分，其余为定轴轮系部分。其相应齿数分别为z1=29，z2=20，z3=24，z4=30，z5=24，z6=30，z7=60，z8=82，z9=18，z10=36，z11=18，z12=24，z13=24。令差动轮系的太阳轮Z4为基本构件a，由电机1调速，差动轮系的行星架Z8为基本构件b由电机2调速，另一个太阳轮Z10为基本构件c，通过齿轮Z13与磁粉加载器相连。

由以上条件可得差动轮系的特性参数:

在该参数下，理论转速灵敏度分别为

为验证构件c对构件a的转速灵敏度，在实验过程中，保持电机2转速不变，调整电机1的转速，观察磁粉加载器的转速状况。为验证转速状态对转速灵敏度的影响，任意选取电机2的7个不同转速进行实验，得到图5a所示的转速关系，图中，nD1、nD2、nL分别为电机1、电机2与磁粉加载器的转速。同理，为验证构件c对构件b的转速灵敏度，保持nD1不变，调整nD2，得到图5b所示的磁粉加载器随电机2变化的转速关系。

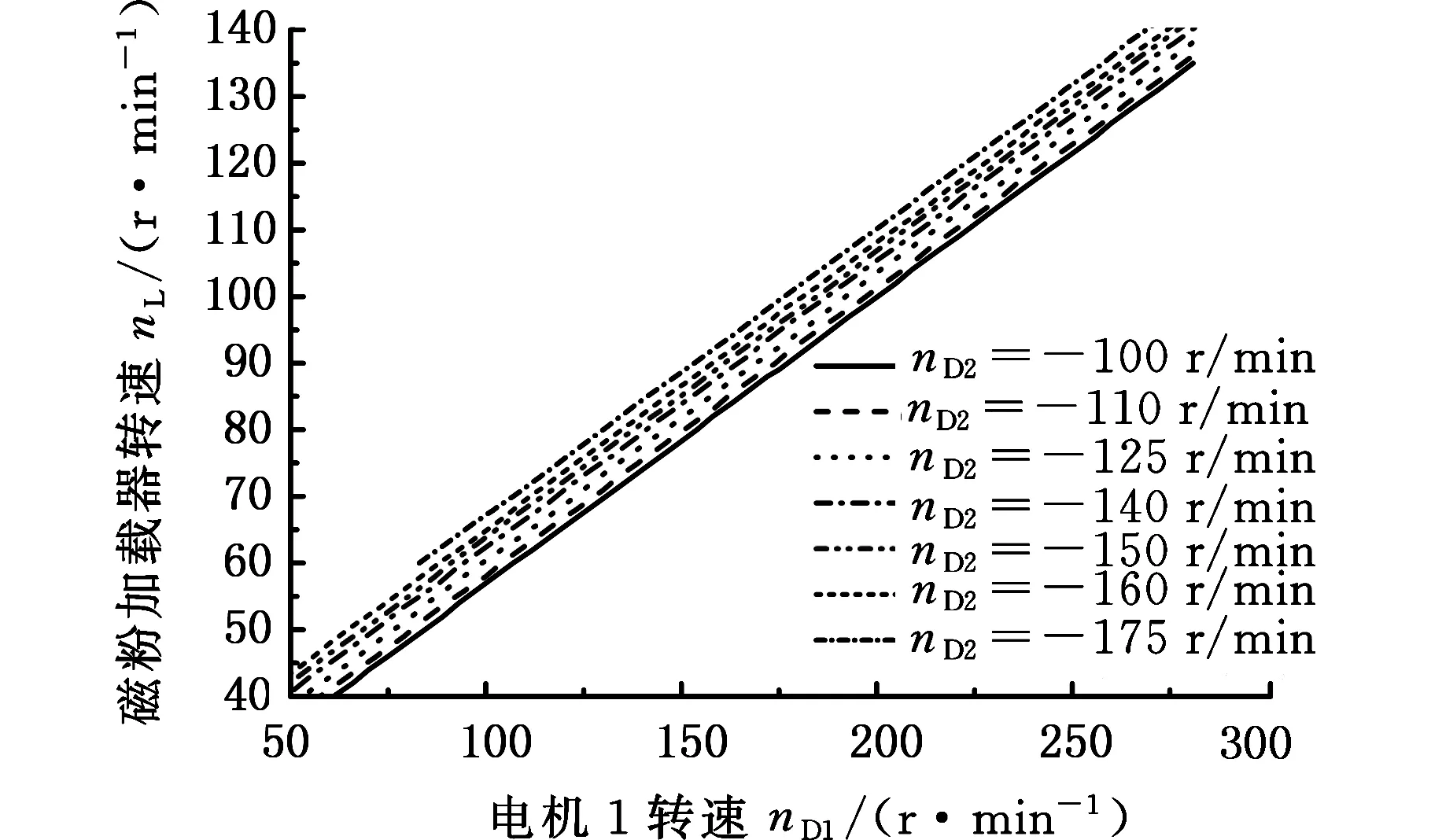
(a)负载随电机1转速变化曲线

(b)负载随电机2转速变化曲线图5 实验测量转速关系图Fig.5 Experimental measured speed curves

由图5可知，nL随nD1(nD2)的变化并不受nD2(nD1)速度状态的影响。将nD1、nD2与nL分别换算到轮系的三个基本构件上，可求得调速过程中构件c对构件a、构件b的转速变化速率即转速灵敏度，得到图6所示的转速灵敏度理论值与实验值对比图，以及表1、表2所示各组实验所得的转速灵敏度与均方根误差。

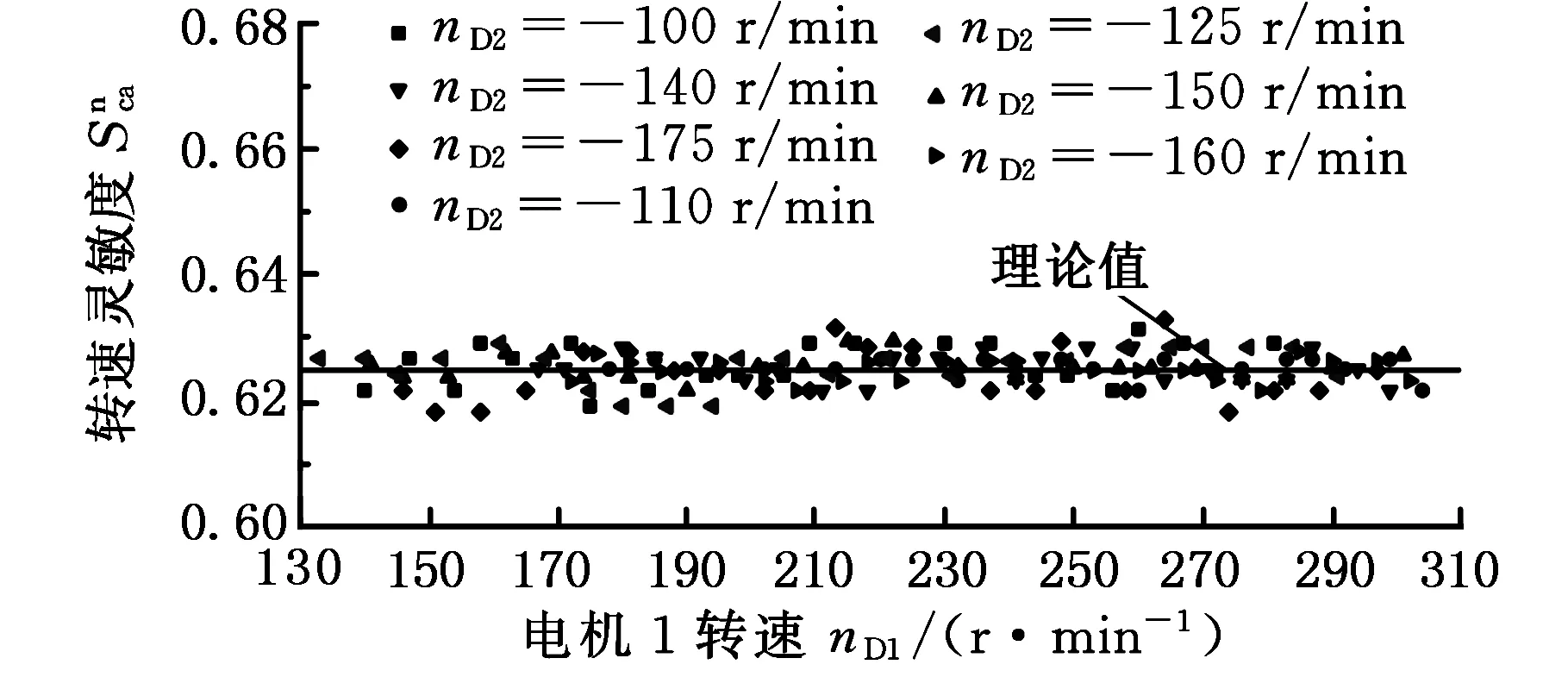
(a)构件c对构件a的转速灵敏度

(b)构件c对构件b的转速灵敏度图6 差动轮转速灵敏度理论与实验值对比图Fig.6 Comparison graph of DGT’s theory sensitivity value with experimental values

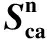
表1 实验所得与均方根误差

表2 实验所得与均方根误差Tab.2 Experimental and root mean square errors

5 差动轮系的动态跟随性能规律与意义

将差动轮系的转速灵敏度以及转速贡献度公式中的K用相对传动比表达，得到构件c随构件a、构件b的转速灵敏度：

(21)

构件a、构件b对构件c的转速贡献度：

(22)

同理，对构件a、构件b的转速灵敏度以及转速贡献度进行分析并以相对传动比进行表达。进而，也可以用相对传动比表达转矩灵敏度、转矩贡献度、功率灵敏度、功率贡献度。由此得到表3所示的差动轮系三个基本构件之间灵敏度与贡献度表达式的总结。观察表3中参数，得出以下规律：

(1)转速灵敏度的下角标与相对传动比的下角标一致。功率灵敏度的数值为-1，转矩灵敏度无意义。

(2)转速贡献度与功率贡献度表达式一一对应，且表达式具有一致的格式：相对传动比的下角标都不出现被分析对象，并以a、b、c逆序排列。

(3)转矩贡献度的下角标与相对传动比的下角标一致但是顺序相反。

行星轮系的相似定理[18]：具有相同特性参数K的行星轮系，所对应基本构件的运动关系和力学关系类似。上述结论与规律对行星轮系通用。

表3 差动轮系动态跟随性能表达式汇总

在差动轮系的设计过程中，研究人员应根据应用需求参照表格选择合适的特性参数以及合理的速度配比。以混合动力汽车为例，若差动轮系分别以发动机与电机作为动力输入，那么应当在静力学分析的基础上，选择能使发动机具有较大转矩贡献度的特性参数并结合转速配比关系使其同时具有较大的功率贡献度。其中转速的配比关系通过综合考虑转速灵敏度以及转速贡献度，结合发动机以及电机的转速特性合理选择以及调节。综上所述，当轮系对动态跟随性能有要求时，在设计过程中应当在静力学分析的基础上综合考虑这6个性能指标，结合轮系负载的特性与原动机的机械特性，找出最优的参数解。

6 结论

(1)深入研究了差动轮系理想模型中各灵敏度与贡献度受转速与特性参数K的影响，总结了各基本构件的转速、转矩、功率状况下的灵敏度与贡献度的表达与规律,并进行了实验验证，得出了各性能指标参数用相对传动比表达的方程。

(2)对转速灵敏度与贡献度的分析说明,各构件之间的转速响应与特性参数有关，而转速的大小与速度配比以及特性参数同时关联。构件之间的转速灵敏度与贡献度不一定一致。功率灵敏度的分析表明，差动轮系各构件对功率变化反应速度恒定。对转矩贡献度与功率贡献度的研究揭示了轮系在工作状态下各基本构件所提供的转矩与功率规律，为载重机械的力矩与功率分配设计提供指导。

(3)本文初次提出差动轮系动态跟随性的研究，这是对轮系运动学分析、静力学分析与动力学分析的补充与完善。在实际应用中，还存在齿轮材料、齿廓形状、加工精度以及安装误差等影响因素，这些因素也是本课题在进一步研究中所需要考虑的。对运动和力的相关影响因素的全面考虑可以使系统在工况突变时能更加快速精确地得到调整。

[1] 郑方焱,张争艳,陈定方,等.新型非圆齿轮分度装置[J].中国机械工程,2014,25(22):2997-3002.

ZHENG Fangyan, ZHENG Zhengyan, CHEN Dingfang, et al. A New Type of Non-circular Gear Index Device[J]. China Mechanical Engineering,2014,25(22):2997-3002.

[2] BOTTIGLIONE F, MANTRIOTA G. Effect of the Ratio Spread of CVU in Automotive Kinetic Energy Recovery Systems[J]. Journal of Mechanical Design,2013,135:061001.1-9.

[3] BOTTIGLIONE F, de PINTO S, MANTRIOTA G. Infinitely Variable Transmissions in Neutral Gear: Torque Ratio and Power Re-circulation[J]. Mechanism and Machine Theory,2014,74:285-298.

[4] 董泳,周绪强,毕强.风力机与液力变速传动装置匹配工作特性研究[J].中国机械工程,2012,23(6):660-666.

DONG Yong, ZHOU Xuqiang, BI Qiang. Research on Working Characteristics about Wind Rotor Matching with HydrodynamicVariable Speed Drive Unit[J]. China Mechanical Engineering,2012,23(6):660-666.

[5] 莫愁,陈吉清,兰凤崇.混合动力汽车动力集成传动机构的设计与分析[J].汽车工程,2016,38(1):36-41.

MO Chou, CHEN Jiqing, LAN Fengchong. Design and Analysis of a Power-integrated Transmission Mechanism for Hybrid Electric Vehicle[J]. Automotive Engineering,2016,38(1):36-41.

[6] 杨阳,马鹏程,秦大同,等.采煤机差动2K-H行星轮系固有特性分析[J].煤炭学报,2016,41(2)：507-512.

YANG Yang, MA Pengcheng, QIN Datong,et al.Analysis of Natural Characteristics of Differential 2K-H Epicyclic Gear Train for Coal Shearer[J]. Journal of China Coal Society,2016,41(2):507-512.

[7] 孙振中.并联HEV用差动轮系特性分析与试验研究[D]. 西安：西安理工大学,2010.

SUN Zhenzhong. Theoretical Analysis and Experimental Study of Differential Gear Train for Parallel Hybrid Electric Vehicle[D].Xi’an: Xi’an University of Technology,2010.

[8] CHEN Chao, CHEN Jiabin. Efficiency Analysis of Two Degree of Freedom Epicyclic Gear Transmission and Experimental Validation[J]. Mechanism and Machine Theory,2015,87(5):115-130.

[9] SALGADO D R, DEL CASTILLO J M.Analysis of the Transmission Ratio and Efficiency Ranges of the Four-, Five-, and Six-link Planetary Gear Trains[J]. Mechanism and Machine Theory,2014,73:218-243.

[10] 马雅丽,张永珍.复杂轮系基本单元的运动特征状态数学建模[J].中国机械工程,2014,25(15):1999-2003.

MA Yali, ZHANG Yongzhen. Kinematic Characteristic State Models for Basic Units of Compound Gear Train[J]. China Mechanical Engineering,2014,25(15):1999-2003.

[11] 孙智民,季林红,沈允文.2K-H行星齿轮传动非线性动力学[J].清华大学学报(自然科学版),2003,43(5):636-639.

SUN Zhimin, JI Linhong, SHEN Yunwen. Nonlinear Dynamics of 2K-H Planetary Gear Train[J]. J.Tsinghua Univ.(Science and Technology),2003,43(5):636-639.

[12] LUO Y T, TAN D. Dynamic Modeling of Planetary Gear Set Considering Meshing Stiffness Based on Bond Graph[J]. Procedia Engineering,2011,24:850-855．

[13] 刘振皓,巫世晶,王晓笋,等.基于增量谐波平衡法的复合行星齿轮传动系统非线性动力学[J].振动与冲击,2012,31(3):117-122.

LIU Zhenhao, WU Shijing, WANG Xiaosun, et al. Nonlinear Dynamics of Compound Planetary Gear Sets Based on Incremental Harmonic Balance Method[J]. Journal of Vibration and Shock,2012,31(3):117-122.

[14] GUO Y, PARKER R G. Dynamic Analysis of Planetary Gears with Bearing Clearance[J]. Journal of Computationl and Nonlinear Dynamics,2012,7(4):041002-041016.

[15] 卫一多,刘凯,崔亚辉,等.齿间滑动摩擦对行星齿轮非线性振动的影响[J].西安理工大学学报，2011,27(3):253-260.

WEI Yiduo, LIU Kai, CUI Yahui, et al.Impacts of Sliding Friction on Planetary Gear Train Nonlinear Vibration[J]. Journal of Xi'an University of Technology,2011,27(3):253-260.

[16] 秦大同,杨军,周志刚,等.变载荷激励下风电行星齿轮系统动力学特性[J].中国机械工程,2013,24(3):295-301.

QIN Datong, YANG Jun, ZHOU Zhigang, et al. Dynamics Characteristic of Planetary Gear System of Wind Turbines under Varying Load[J]. China Mechanical Engineering,2013,24(3):295-301.

[17] 王振,崔亚辉,刘凯,等. 装备单环路系统的整车行驶动力学研究[J]. 中国机械工程,2016, 27(8):1123-1129.

WANG Zhen, CUI Yahui, LIU Kai, et al.Research on Driving Dynamic for Vehicles Equipped with a Single Loop System[J]. China Mechanical Engineering,2016,27(8):1123-1129.

[18] 崔亚辉．功率分汇流行星传动的研究[D]. 西安：西安理工大学,1998.

CUI Yahui.Study on the Bifurcated Power Planetary Transmission[D]. Xi’an: Xi’an University of Technology,1998.

DynamicTrackingPerformanceAnalysisofDifferentialGearTrains

XU Lin LIU Kai CUI Yahui MENG Peiyuan

School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an,710048

The speed, torque and power of three DGT’s basic components were analysed, and the concepts of sensitivity and contribution were studied. The parameters and rules that affected the sensitivity and the contribution were analyzed, and corresponding expressions were obtained in the end. In order to verify the speed sensitivity calculation method the tests were completed. The research results show that, sensitivity of speed and contribution torque of three basic components are only associated with the characteristic parameters of DGT, contribution expressions of speed and power are determined by the characteristic parameters and speed matching relationship of differential gear systems. Sensitivity and contribution reflect the dynamic tracking performances of DGT，and provide guidances for selection and design of DGT.

differential gear train(DGT); sensitivity; contribution; dynamic tracking performance

TH132.41

10.3969/j.issn.1004-132X.2017.23.014

2016-11-25

国家自然科学基金资助项目(51175419)

(编辑袁兴玲)

徐琳，女，1987年生。西安理工大学机械与精密仪器工程学院博士研究生。主要研究方向为行星齿轮传动功率流分析。刘凯，男，1957年生。西安理工大学机械与精密仪器工程学院博士研究生导师。崔亚辉，男，1963年生。西安理工大学机械与精密仪器工程学院博士研究生导师。孟培媛，女，1986年生。西安理工大学机械与精密仪器工程学院博士研究生。