基于空间填充法的刀具路径生成算法及其仿真
2017-12-15隋秀凛陈晓奇
隋秀凛 陈晓奇 焦 艳 廉 冲
哈尔滨理工大学机械动力工程学院,哈尔滨,150080
基于空间填充法的刀具路径生成算法及其仿真
隋秀凛 陈晓奇 焦 艳 廉 冲
哈尔滨理工大学机械动力工程学院,哈尔滨,150080
针对空间填充曲线法的网格只具有正则矩形,生成的刀具路径存在频繁转向、长度冗长、生成时间长等缺点,提出一种基于空间填充法的刀具路径生成算法。选用T样条曲面为造型曲面,生成具有非正则矩形的网格并进行回路的规划;用改进的Hamiltonian算法初步生成刀具路径;用改进的倒圆角算法进行拐角优化,获得最终的刀具路径。开发出了基于该算法的仿真系统,对算法进行了仿真验证和实际的加工实验,结果表明所提出算法有效可行,生成的刀具路径长度及生成时间都得到缩短。
空间填充曲线; T样条曲面;Hamiltonian算法;倒圆角算法
0 引言
机械、航空等领域技术的飞速发展对产品的性能和外形提出了更高的要求,被加工的曲面也随之变得越来越复杂。目前数控机床或者加工中心多采用行切法、环切法以及空间填充曲线(space-filling curve,SFC)法进行加工制造,而空间填充曲线法在复杂曲面加工上的应用优于其他两种加工方法[1-3]。空间填充曲线法是一种降低空间维度的方法,它将数据从高维度向低维度映射,使用经典线性索引结构存储数据。常用的空间填充曲线有Hilbert 曲线、Gray曲线和Z曲线。虽然国内外学者对空间填充曲线法在刀具路径规划中的运用进行了不同程度的研究,但是空间填充曲线法还是存在着许多问题有待解决,例如:刀具路径从参数空间到实际加工表面的映射问题;由于网格的划分均采用正则的矩形,面对复杂曲面如何进行合理的细化和分割问题;生成的刀具路径均存在的刀具频繁转向问题[4-6]。
T样条曲面是一种具有水密性的造型曲面,在构建模型时不需进行面片裁剪和拼接,是一个单一的全曲面,具有统一的数学表达式[7-8],并且T样条曲面具有的参数空间和欧氏空间存在一一映射的关系,数据的拓扑结构和网格的结构完全相同,因此可以极大地降低刀具路径从空间到实际加工表面的映射难度[9]。同时,由于T样条曲面在构建网格时允许T节点的存在,所以其划分存在非正则矩形,从而可以更好地表达曲面[10-11]。因此本文提出一种基于空间填充曲线法的刀具路径生成算法。首先,选用T样条曲面作为造型曲面,对工件进行建模,根据设置的限定残高等切削参数,在参数空间生成具有非正则矩形的网格,进行回路的规划;然后,制定回路合并所产生的代价策略,用改进的Hamiltonian算法对回路进行合并处理,初步生成刀具路径;最后,用改进的倒圆角算法进行拐角优化,得到参数空间的整体刀具路径,最终映射到实际空间得到指导实际加工的整体刀具路径。
1 T样条曲面的网格和回路
1.1 网格的划分与生成
以T样条曲面为造型曲面,对实际加工的工件进行建模,确定工件的欧氏空间与参数空间。选取参数空间为刀具路径的规划空间,将参数空间的刀具路径映射到欧氏空间内,即可得到实际的刀具路径。在参数空间内,依据等残留高度法原理[12-14],以限定残高为条件,进行网格的划分与生成。
设参数空间网格曲面的表达式为
S=S(u,v)
(1)
给定限定残高ε,当曲面为凹曲面时,ε与曲面曲率半径ρ、刀具有效半径Re以及切削宽度l满足如下关系:
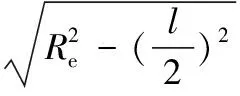
(2)
当曲面为凸曲面时,满足如下关系:

(3)

根据同样原理,在u方向上也可以生成一系列的偏置参数线,将u方向的参数线与v方向的参数线相互交叠,就得到参数域上的网格,所得的交点即设定为网格的网格点。
1.2 回路的规划
若将可形成矩形的相邻4个网格点连接在一起,那么连接后的矩形即为一个回路,其中网格点之间的连线称之为回路的边。图1所示灰色区域为参数空间中工件的形状。依据1.1节方法生成网格,图1a所示为网格点构成的无向图G。以初始参数线上的网格点为初始网格点,寻找相邻的其余三个网格点,并且对非法的回路进行合理的处理,可生成图1b所示的用于刀具路径生成的对偶图G′。

(a)无向图G (b)对偶图G′图1 回路生成示意图Fig.1 Diagram of loop generation
与传统的张量积曲面不同,由于T样条曲面在建模时是单一的全曲面,所以会覆盖工件上不规则的边界与孔洞。在构建网格时,网格内的网格点可能落入孔洞之中或不规则边界之外,在回路生成时会有不同的影响。图1a中A、B、C、D 4种情况可能无法生成回路,针对这些情况,本文制定了4种处理规则,如图2所示。

(a)情况A (b)情况B

(c)情况C (d)情况D图2 非法回路处理规则Fig.2 Rules of illegal loop
(1)情况A。造成此情况的原因是在生成网格时存在奇数列或行,使得边界部分不包含在网格内,无法构成回路。针对此情况,遵循图2a所示的处理规则:设Pa1、Pa2为奇数列或行上的网格点,在边界曲线上取两点Pa3、Pa4,并且规定Pa1Pa3、Pa2Pa4与Pa1Pa2垂直,使Pa3、Pa4满足构成回路的4个网格点的条件,与Pa1、Pa2组成新的回路。


(4)情况D。造成此情况的原因是在生成网格时构成回路的4个网格点完全落在孔洞之内。针对此情况(图2d),在进行后续的刀具路径规划时可以舍弃,不作处理。
2 刀具路径的规划
2.1 刀具路径的生成
2.1.1回路的合并代价
如何对回路进行合并,将决定怎样生成刀具路径,因此确定回路合并的代价函数是十分重要的。设合并的代价函数为Cost(*),影响Cost(*)的因素包括刀具的姿态、刀具路径的长度以及当前状态的加工条件等,根据已确定的影响因素,由下式获得Cost(*)的大小:
Cost(*)=(VwV+LwL+CwC+…)
(4)
其中,V表示刀具的姿态;wV为刀具姿态的影响权重;L为刀具路径的长度,wL为刀具路径长度的影响权重;C为当前状态的加工条件;wC为当前状态加工条件的影响权重。这些影响因素可以根据实际加工的要求进行人为设定,在这里仅考虑影响因素V和L,并且设定wP=wL=1,即认定V与L是同样重要的影响因素。
如图3a所示,回路A与回路B、C、D、E相邻。以回路A与B合并为例(其中e、f为回路A与B相对的实边,g、h为合并时需要连接的虚边),在回路A时刀具的姿态为VA,在回路B时刀具的姿态为VB。根据下式可得回路A与B合并时所付出的代价Cost(A,B):
(5)
同样,依据式(5)可获得回路A与回路B、C、D、E进行合并时各自的合并代价,并通过Cost(A,B)、Cost(A,C)、Cost(A,D)与Cost(A,E)相互比较,确定回路A与哪个回路的合并代价最小。假如回路A与B的合并代价值最小,那么将回路A与B进行合并,生成图3b所示的新回路A″。

(a)合并之前 (b)合并之后图3 回路合并Fig.3 Coalition of loops
2.1.2改进的Hamiltonian算法
Hamiltonian算法是一种简单且高效的轨迹解决算法,该算法是一种覆盖合并算法,可以在任何矩形网格中得到拓展应用[1-2,16]。但是该算法是以生成的网格存在奇数列或行为基础进行演算的,并且构建网格的行或列都是正则的,而根据第1节中网格的生成特点以及回路的生成方法,以及2.1.1节确定的合并代价算法,生成的回路无向图G覆盖在工件表面,整体形状如工件形状,生成的行或列需要进行不同程度的修剪,使得原Hamiltonian算法不能完全适应生成的回路无向图G,因此本文对Hamiltonian算法进行改进,具体实现步骤如下(图4,其中,图4a表示无向图G,图4b表示对偶图G′,图4c为生成的刀具路径):
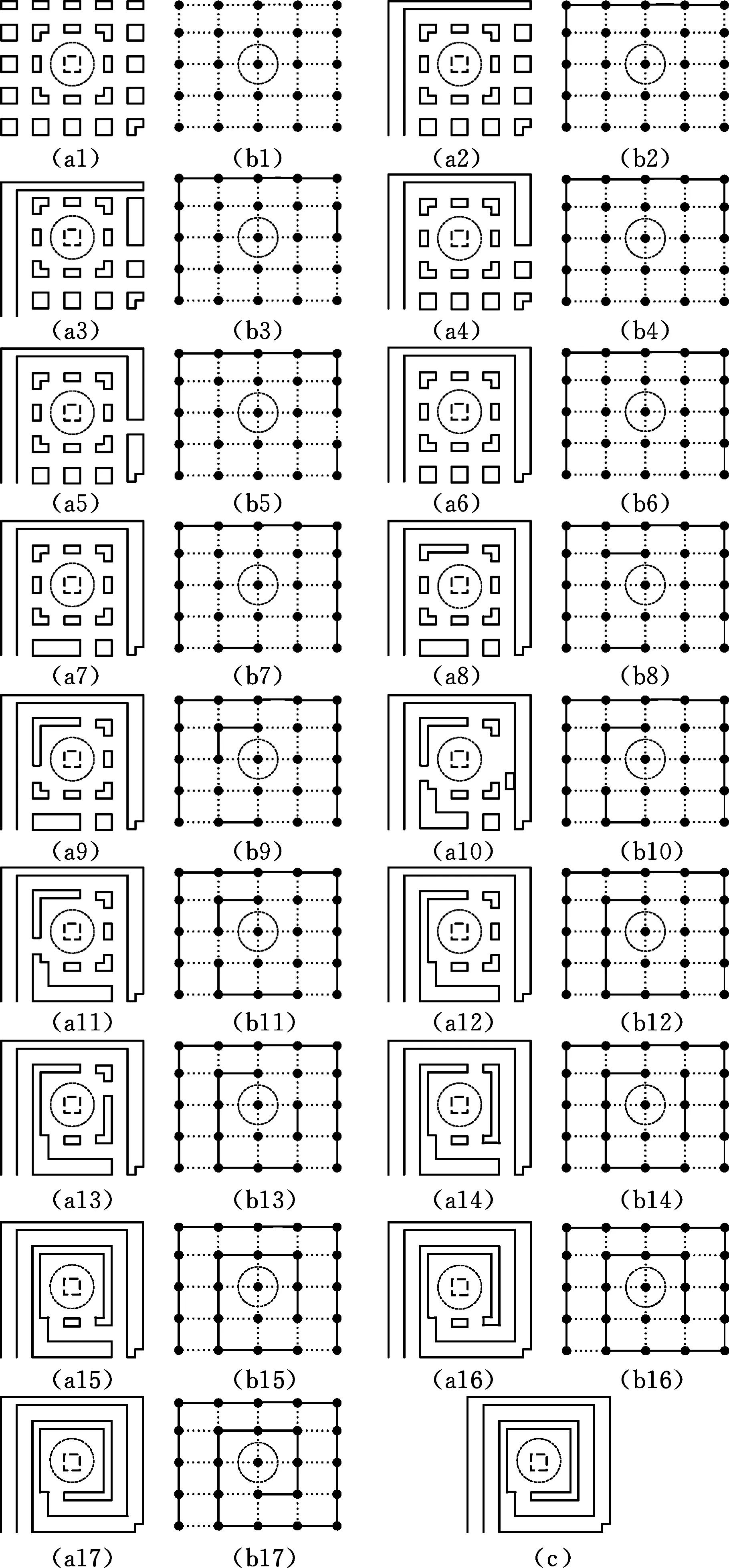
图4 刀具路径生成示意图Fig.4 Schematic diagram of toolpath generation
(1)设集合M为刀具路径的最小生成树集合,并规定M为空集。针对非正则的行或列,在对偶图G′中取外围的节点为边界点,设边界点数为m。如图4b2所示,取图中某一节点,以逆时针方向取m/4~m/2个边界点,不考虑这些回路的合并代价,将这些边界点进行连接,相应回路进行合并,生成初始的特殊回路(图4a2)并放入集合M中。
(2)对于图4b所示的对偶图G′,将剩余的节点都作拟合并处理,得到每条边的合并代价,以合并代价的数值大小为依据进行升序的排序。
(3)根据步骤(2)所得的边的序列,将第1个元素的2个回路进行合并,得到图4b3所示的新边,即合并代价最小的边,若该边两端的节点与集合M内其他节点相连接,在其对偶图G′中不构成回路,并且满足合并代价的要求,则将该边以及相应的节点加入到集合M中;若构成回路,则此条边以及相应的节点不能加入到集合M中。
(4)若将边放入集合M中,存在于M中的两个节点就相互连接,即对偶图G′中的两个节点相互连接,图4a3所示的相应的无向图G中两个回路相连接生成新的回路,则进入步骤(5),否则返回步骤(3)。
(5)如果集合M内存在n-1条边线(其中n为对偶图G′中节点的数量),则停止回路的合并,此时的集合M即为刀具路径的生成结果集合,将集合M进行输出即可生成图4c所示的刀具路径,否则返回步骤(3)。
2.2 刀具路径的优化
尽管采用了改进的Hamiltonian算法进行刀具路径的规划,但是生成后的刀具路径依旧存在很多90°的直角拐角,这在实际的加工过程中会导致进给方向频繁转向,对机床和刀具都带来极大的冲击,同时还会导致加工表面质量下降,因此需要对改进的Hamiltonian算法生成的刀具路径进行优化处理。
倒圆角过渡算法的原理就是把直角过渡替换成相切圆的圆弧过渡,使拐角处的直线部分与圆弧相切,在进行加工时实现圆弧过渡,从而减小冲击[6]。但是倒圆角过渡算法是应用在正则矩形的网格上,而本文生成的网格具有非正则的矩形,因此本文提出了一种改进的倒圆角过渡算法。
根据倒圆角算法的原理,需要寻找相切点,因此本文提出了一种寻找相切点的方法来改进倒圆角过渡算法,其具体实现如下:
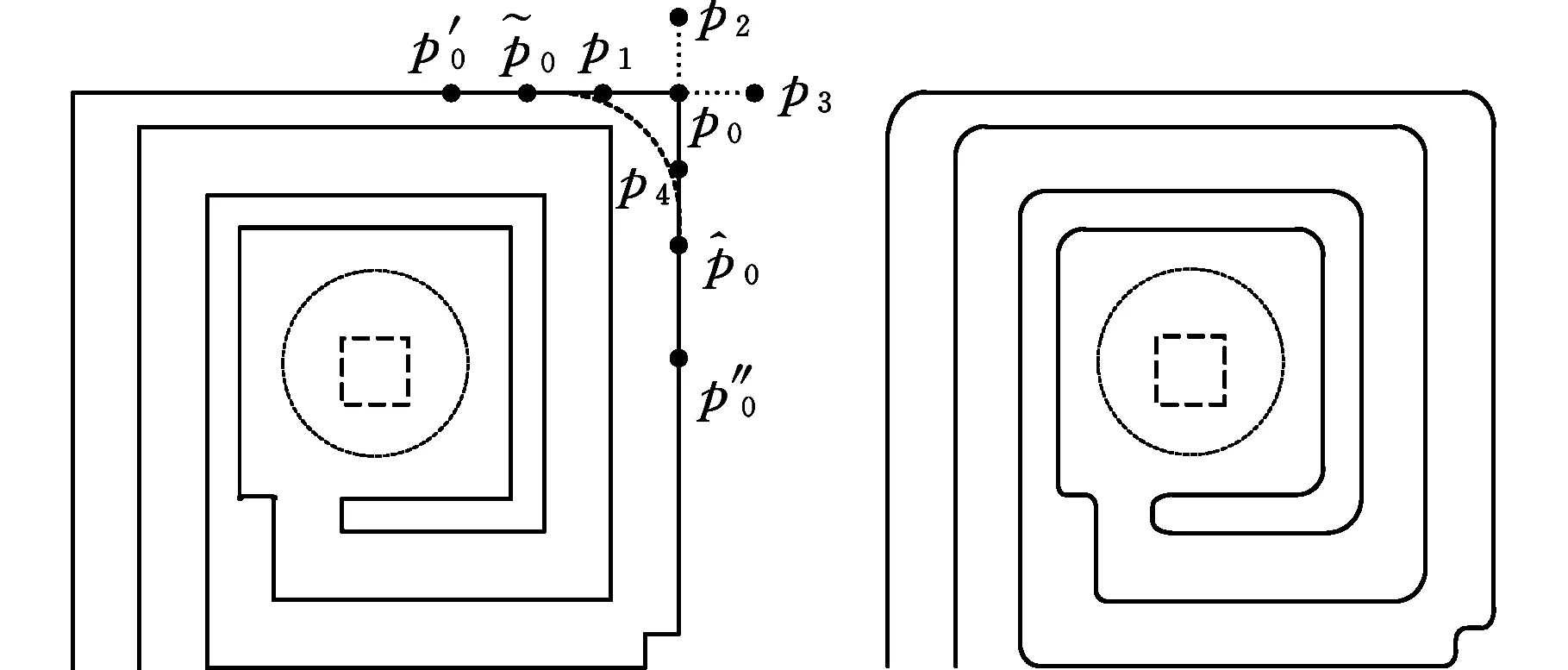
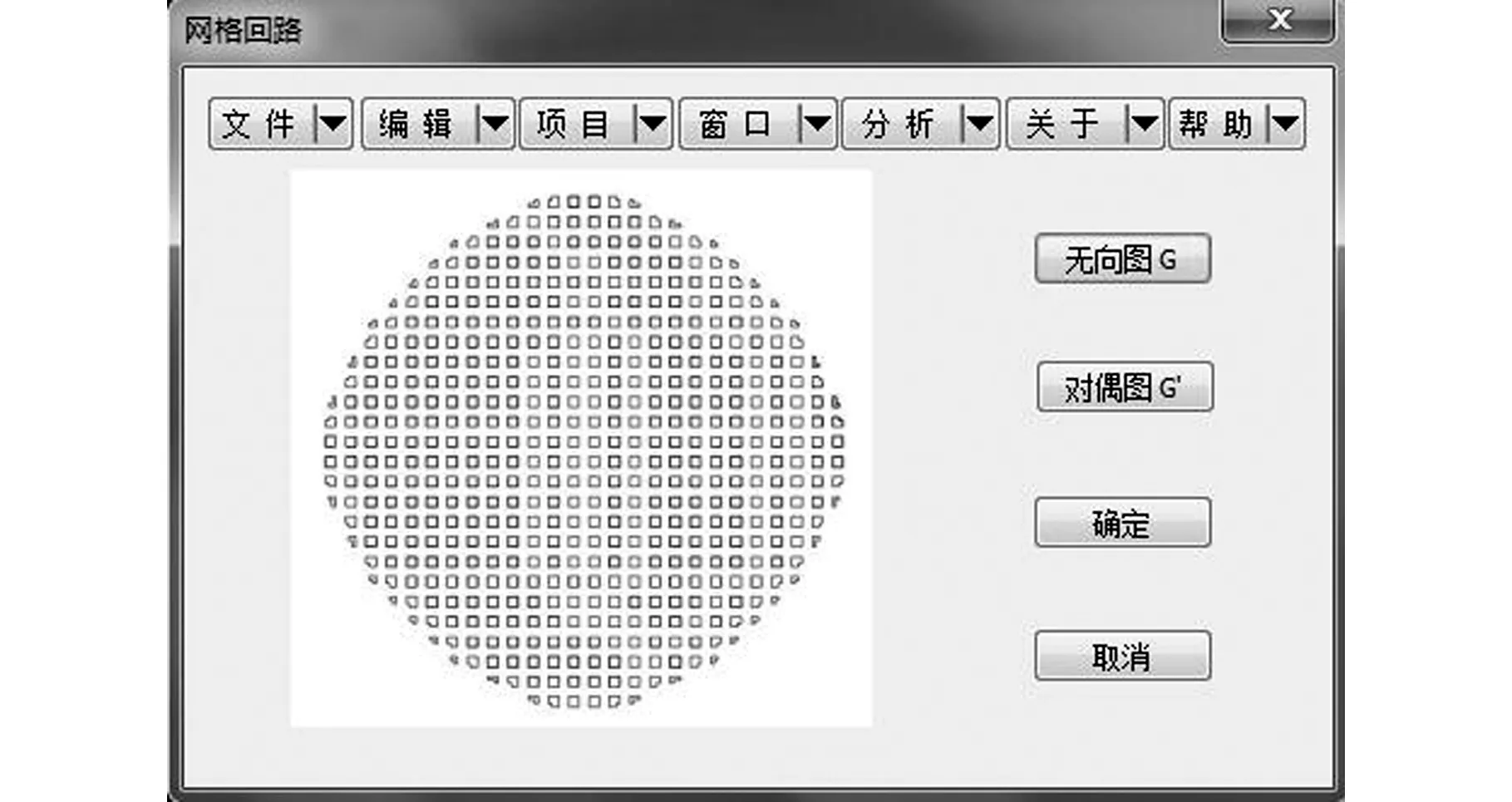
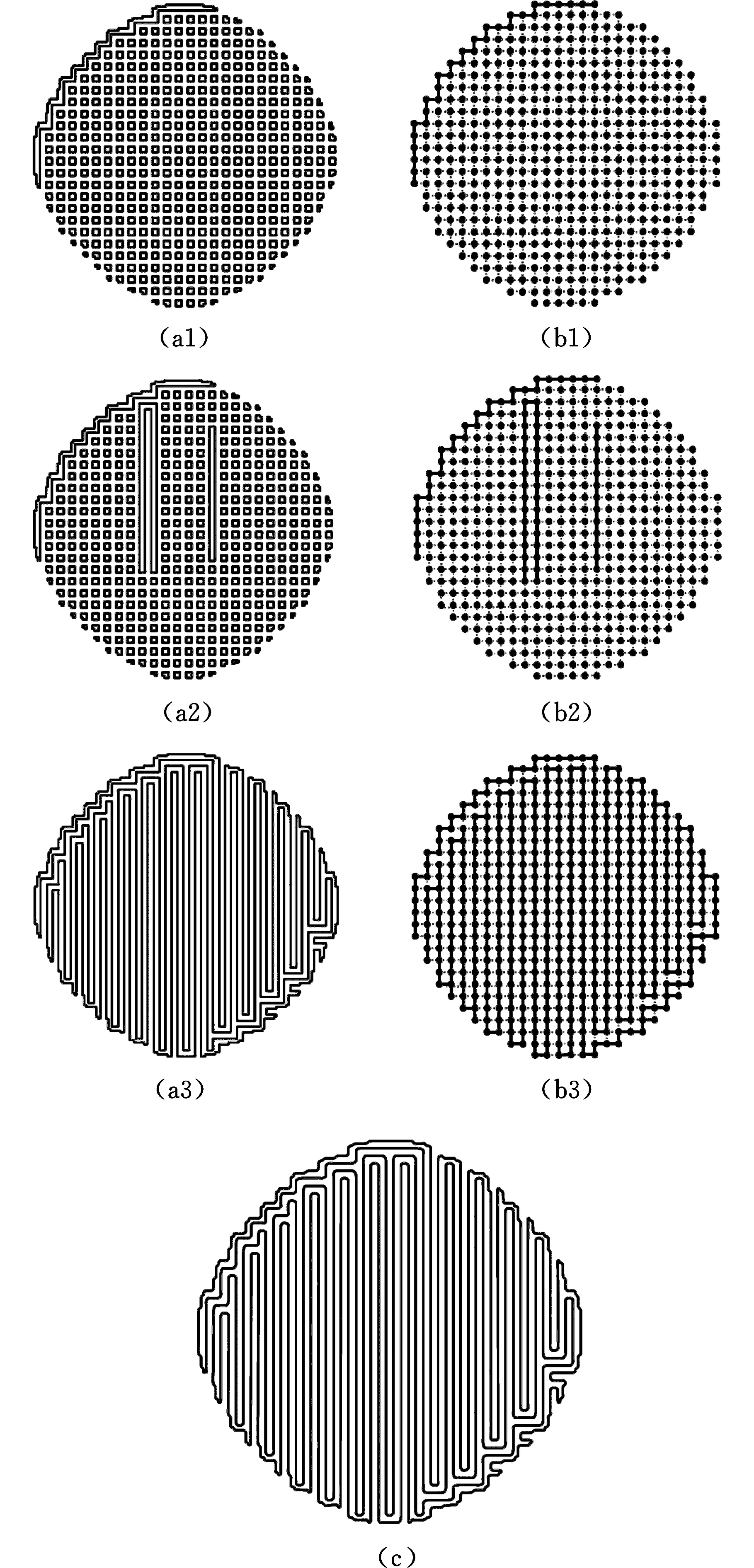
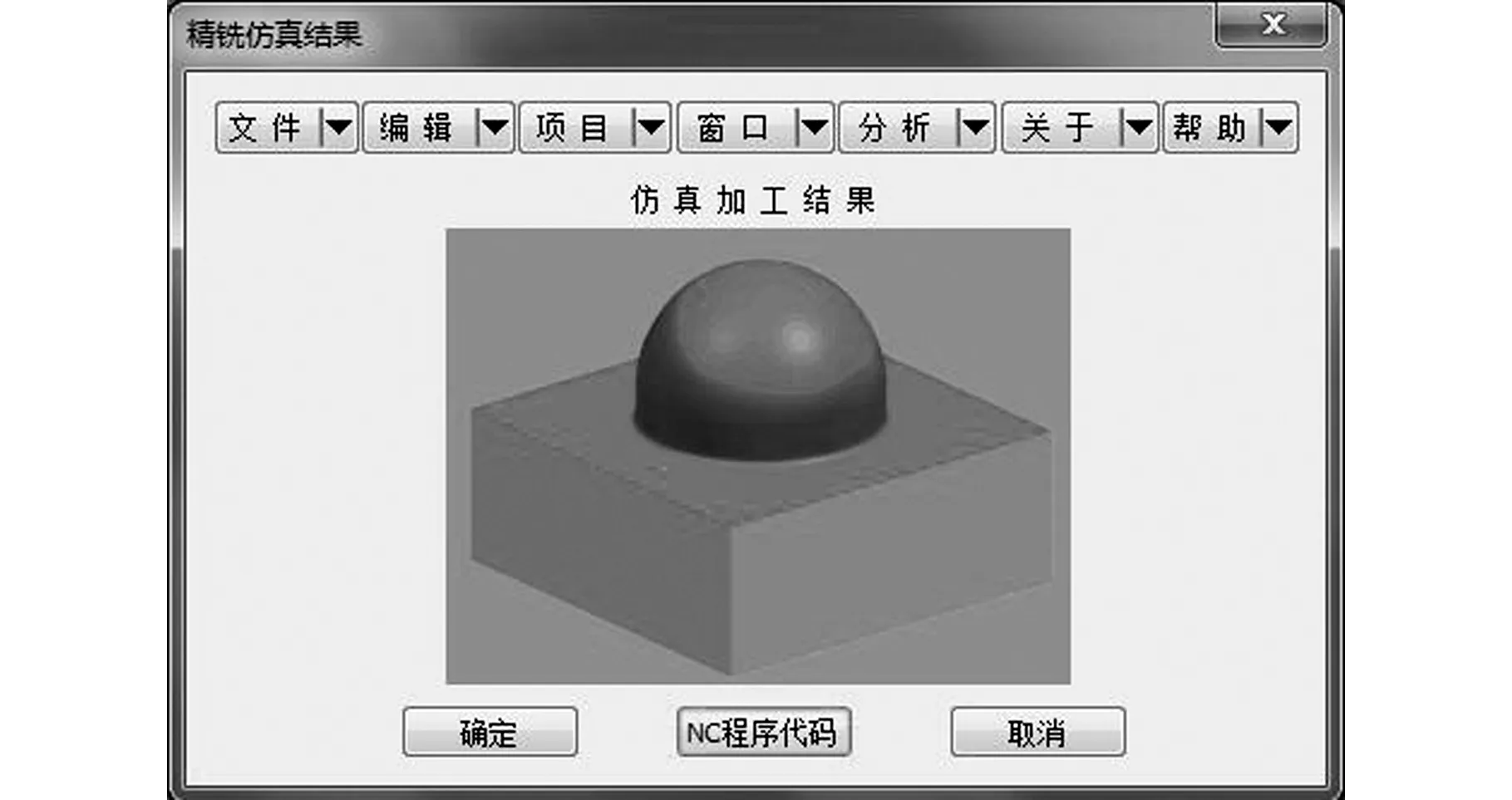
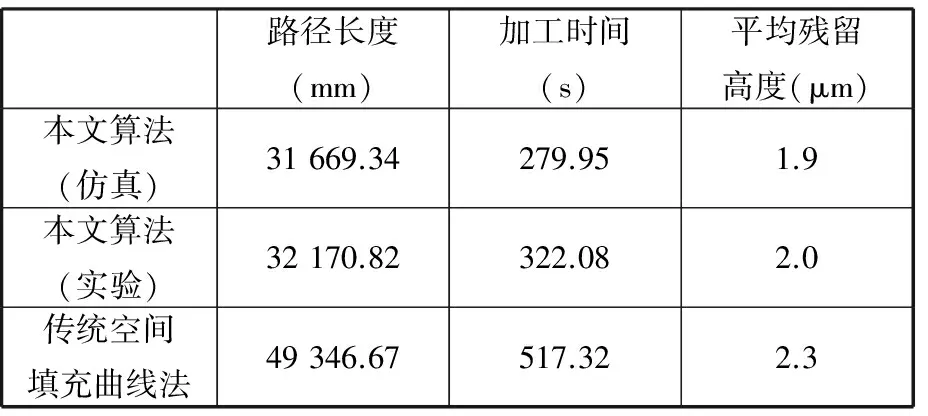
(1)根据第1节构建网格时生成u、v方向的参数线不同的偏置距离lu和lv,设定偏置距离d,并且满足0 (2)如图5a所示,p0为某一网格点,根据步骤(1)中的偏置距离d分别向4个方向进行偏置得到4个点p1、p2、p3和p4。根据生成的4个偏置点p1、p2、p3、p4的坐标信息,判断其是否在已生成的刀具路径上面。 (3)根据刀具路径的生成情况,偏置点最多有2个存在于刀具路径上。若只存在1个偏置点在刀具路径上,则表明该点是刀具路径的起始点或者终点;若2个偏置点的纵坐标相同(如图5a中的p1与p3)或者2个偏置点的横坐标相同(如图5a中的p2与p4),则表明在网格点p0处不存在拐角,此处的刀具路径是直线型的。若2个偏置点的横坐标与纵坐标均不相同(如图5a中的p1与p4),则表明在网格点p0处存在拐角,此处的刀具路径呈直角型转向。 (6) 依据上述改进算法,对生成的网格中的网格点从上到下、从左到右进行遍历,进行拐角的判断与优化,最终可获得图5b所示的优化后的刀具路径。 (a)优化策略(b)优化后的刀具路径图5 刀具路径的优化Fig.5 Optimization of toolpath 此时生成的刀具路径存在于T样条曲面的参数空间内,依据参数空间与欧氏空间一一映射的关系,将得到的刀具路径从参数空间向欧氏空间映射,即可得到存在于欧氏空间中的工件表面实际的加工刀具路径。 本文采用Microsoft Visual Studio 2010 为开发平台,以Open GL为图形引擎核心,依据上述方法,开发出基于空间填充曲线法的数控精铣仿真系统,图6为会员登陆后系统的主要操作界面。 图6 系统主要操作界面Fig.6 Interface of simulation system 在标题栏中“文件”处可以导入待加工的工件信息文件;图6左侧的空白矩形窗口可以显示导入的工件模型;参数窗口可以设置切削参数和刀轴参数;网格窗口是依据前面设置的参数信息生成的网格信息,可以查看u方向的v参数线、v方向的u参数线以及生成的整体网格;回路窗口是依据回路的处理规则进行规划后的回路情况,可以查看回路的无向图G和对偶图G′;刀具路径窗口是依据前面得到的回路信息和工件信息进行刀具路径的规划,可以查看回路合并时不同序列的无向图G与对偶图G′、整体刀具路径的无向图G与对偶图G′,以及采取优化算法生成的优化后的刀具路径;仿真加工窗口是依据前面得到的优化后的刀具路径,将其映射到实际欧氏空间,在工件表面进行仿真加工,可查看加工的仿真结果,并可以得到相应的可用于实际加工的NC程序代码。 本文以钢盔为加工工件进行仿真实验。首先在“文件”处导入钢盔的信息文件,然后在参数窗口设置表1所示的切削参数。对刀轴参数进行设置,如表2所示。 表1 切削参数 表2 刀轴参数 根据表1和表2设置的参数,在网格窗口生成相应的网格,然后根据生成的网格信息和所获得工件信息,对回路进行规划,规划后的回路情况如图7所示。 (a)无向图G (b)对偶图G′图7 规划后的回路Fig.7 The planned loop 图7a所示为依据回路处理原则生成的无向图G,通过对回路的划分和重新生成,构建了一个圆形区域的无向图;图7b为相应的对偶图G′,可以看出其形状也近似为一个圆形。 刀具路径窗口将根据图7所生成的回路,运用改进的Hamiltonian算法对刀具路径进行规划,生成图8所示的刀具路径,其中,图8a为无向图G,图8b为对偶图G′,图8c为优化后的刀具路径。 图8 刀具路径生成规划示意图Fig.8 Generation of toolpath 图8a1所示为相邻边界上不计代价进行回路合并而生成的初始路径,并且该路径并非是封闭的回路曲线,其起始点与终点是分开的,成一条单独的路径,其拐角处呈90°直角;图8b1为相应的对偶图,代表相应回路的对偶节点已经通过边线连接起来;图8a2为第43次回路合并后的刀具路径图,除了初始路径外,根据合并代价的大小,已经生成了2个新的不同的回路,在其对应的对偶图(图8b2)中,相应的对偶节点也通过边线连接起来,但无论初始路径还是新生成的回路路径,其拐角处依旧是90°的直角;图8a3所示为生成的整体刀具路径,此时的路径是一条单连通、无回路的复杂曲线,其对偶图(图8b3)所有的对偶节点都通过边线连接起来,并且不构成回路,但是生成的刀具路径在拐角处仍然均是90°的直角;如图8c所示,经过改进的倒圆角过渡算法的优化,生成后的刀具路径在拐角处呈圆弧过渡,不存在90°的直角拐角。 图8c所示的优化后的刀具路径存在于空间填充曲线的参数空间中,将其映射到实际欧氏空间进行仿真加工,其仿真结果如图9所示。由图9可知,所开发的仿真系统可以实现本文提出的基于空间填充曲线法刀具路径的生成算法,并且可以进行完整的仿真操作。 图9 仿真加工结果Fig.9 Simulation result of machining (a)加工过程 (b)加工结果图10 实际加工图Fig.10 Actual processing 依据表1与表2的加工参数,在XH715立式加工中心上进行了实际的加工实验,如图10所示。如图10a所示,使用激光测量仪对加工时的路径长度进行监测,并同时记录加工所用的时间,加工后的结果如图10b所示。随机测量加工后的工件上200个采样点处的残留高度,得到的平均残留高度、加工时间及路径长度结果如表3所示。 表3 实验结果 由表3结果可知,使用本文开发的仿真系统的仿真结果与实际加工所获得的结果数值相差不大,生成的刀具路径长度、加工时间以及平均残留高度的相对误差不超过10%,表明本文开发的仿真系统能够满足实际加工要求,符合实际加工的标准,本文算法是有效可行的。同时表3结果表明:与传统的空间填充曲线法相比较,运用本文提出的刀具路径生成算法生成的刀具路径总长度减小17 175.85 mm,缩短了加工长度;加工时间缩短195.24 s,提高了加工效率;生成的平均残留高度减小了0.3 μm,提高了加工精度。 本文提出了一种基于空间填充曲线法的刀具路径生成算法:选用T样条曲面为造型曲面,依据限定残高,生成具有非正则矩形的网格,并进行回路的规划;依据回路的合并代价,用改进的Hamiltonian算法初步生成刀具路径;用改进的倒圆角算法进行拐角优化,获得最终的刀具路径。利用VS2010和OpenGL开发了基于该算法的仿真系统,并进行了仿真实验,同时进行了实际的加工验证。结果表明,仿真结果与实际加工结果的刀具路径长度、加工时间以及平均残留高度相对误差在10%以内,证明了本文算法的有效性,同时表明开发的仿真系统可以满足实际加工的要求;与传统空间填充曲线法相比,本文算法生成的刀具路径长度减小17 175.85 mm,加工的时间缩短195.24 s,生成的平均残留高度减小0.3 μm,表明本文方法生成的刀具路径长度更短,生成时间更短,同时还能满足加工精度要求。 [1] 黄象珊. 基于适应性空间填充曲线生成刀具路径的技术研究[J]. 组合机床与自动化加工技术, 2014(1): 53-56. HUANG Xiangshan. Research of Technology Tool Path Based on the Adaptability Space Filling Curve Comes into being Cutter Route’s[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014(1): 53-56. [2] 淡卜绸,张锋涛,雷改丽. 基于网格曲面上空间填充曲线刀具路径生成算法研究[J]. 机械设计与制造, 2011(7):93-95. DAN Bochou,ZHANG Fengtao,LEI Gaili. Arithmetic Research for Generating Tool Path of Space-filling Curves Basedon Subdivision Meshes Surface[J]. Machinery Design & Manufacture,2011(7):93-95. [3] XU Rufeng, CHEN Zhitong, CHEN Wuyi. Tool Positioning Algorithm Based on Smooth Tool Paths for 5-axis Machining of Sculptured Surfaces[J]. Chinese Journal of Mechanical Engineering, 2011,24(5):851-858. [4] CHEN Z C, KHAN M A. A New Approach to Generating Arc Length Parameterized NURBS Tool Paths for Efficient Three-axis Machining of Smooth, Accurate Sculptured Surfaces [J]. The International Journal of Advanced Manufacturing Technology, 2014,70(5/8): 1355-1368. [5] 李万军. 基于分形中Hilbert曲线的复杂曲面加工刀具轨迹规划算法研究[D].南京:南京航空航天大学,2012. LI Wanjun. Research on Algorithms of Tool Path Generation of Complex Surface Machining Based on the Hilbert Curve in Fractal Theory[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. [6] 李德信,焦俊鹏. Hilbert填充曲线用于刀具路径生成的算法及改进研究[J]. 中国机械工程, 2011,22(22): 2739-2743. LI Dexin, JIAO Junpeng. Research on Tool Path Generation Algorithm and Improvement Based on Hilbert Space-filling Curves[J]. China Mechanical Engineering ,2011,22(22): 2739-2743. [7] 李新. T样条和T网格上的样条[D].合肥:中国科学技术大学,2008. LI Xin. T-splines and Splines Over T-meshes[D]. Hefei: University of Science and Technology of China, 2008. [8] NASRI A, SINNO K, ZHENG J. Local T-spline Surface Skinning [J]. The Visual Computer,2012, 28 (6): 787-797. [9] 彭小新,唐月红. 自适应T样条曲面重建[J]. 中国图象图形学报, 2010,15(12): 1818-1825. PENG Xiaoxin, TANG Yuehong. Automatic Reconstruction of T-splines Surfaces[J]. Journal of Image and Graphics, 2010, 15(12): 1818-1825. [10] WANG Aizeng, ZHAO Gang. The Analysis of T-spline Fairness[J]. Computer-aided Design and Applications, 2013, 10 (5):817-825. [11] 乔桂新,温维亮,郭新宇,等. 基于T样条拼接的彩椒果实可视化研究[J]. 系统仿真学报, 2012,24(6): 1227-1231. QIAO Guixin , WEN Weiliang , GUO Xinyu, et al. Research on Visualization of Bell Pepper Fruit Based on T-Splines Merging[J]. Journal of System Simulation , 2012, 24(6): 1227-1231. [12] 杨旭静,王小芳,郑娟,等. 基于包络面的网格曲面等残留高度路径规划[J]. 湖南大学学报(自然科学版), 2013,40(10):38-42. YANG Xujing, WANG Xiaofang, ZHENG Juan, et al. Constant Scallop-height Tool Path Generation for Mesh Surface Based on Tool Envelope Surface. Journal of Hunan University (Natural Sciences). 2013,40(10):38-42. [13] DUVEDI R K, BATISH A, BEDI S,et al. Scallop Height of 5-axis Machining of Large Triangles with a Flat End Mill[J]. Computer -Aided Design and Applications,2015, 12 (6):710-716. [14] 韦尧兵,廖波,李运. 基于等残留高度的自由曲面加工刀具轨迹规划[J]. 新技术新工艺, 2013(12):63-65. WEI Yaobing, LIAO Bo, LI Yun. Toolpath Plan for the Free-form Surfaces Machining Based on ISO-scallop[J]. New Technology & New Process, 2013(12):63-65. [15] 庄鑫. T样条局部细分算法的改进[D].大连:大连理工大学,2010. ZHUANG Xin. The Improvement on the T-spline Local Refinement Algorithm[D]. Dalian: Dalian University of Technology, 2010. [16] 李万军,牛敏. 多岛屿曲面的刀具轨迹规划算法研究[J]. 组合机床与自动化加工技术,2015(5):123-126. LI Wanjun,NIU Min. Research on Tool Path Planning Algorithm of Multi-island Surface.[J] Modular Machine Tool & Automatic Manufacturing Technique, 2015(5): 123-126. ToolpathGeneratingMethodandSimulationBasedonSpace-fillingCurves SUI Xiulin CHEN Xiaoqi JIAO Yan LIAN Chong School of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin,150080 In view of grids for space-filling curve were regular rectangles, and toolpath constructed on space-filling curve had defects such as frequent turns, tediously long lengths, long generation time, etc. A tool path generation algorithm was proposed based on space-filling curve. T-spline surfaces were regarded as modeling surfaces for generating grids with irregular rectangles, and a loop planning was performed. And then an improved Hamiltonian algorithm was used for generating tool path preliminarily. At last, the whole tool paths which could be obtained based on optimized corner by using an improved fillet algorithm. A simulation system was developed to verify the tool paths generation algorithm, and the algorithm was also tested by the actual machining. The results show that the algorithm is effective and feasible, and it will reduce lengths and time costs of tool-path’s generatons. space-filling curve; T-spline surface; Hamiltonian algorithm; fillet algorithm TH164 10.3969/j.issn.1004-132X.2017.23.010 2016-08-09 哈尔滨市科技创新人才研究专项基金优秀学科带头人项目(2013RFXXJ064) (编辑苏卫国) 隋秀凛,女,1962年生。哈尔滨理工大学机械动力工程学院副院长、教授。主要研究方向为计算机集成制造技术、虚拟制造技术、数控技术。发表论文20余篇。E-mail:xiulinsui@163.com。陈晓奇,男,1989年生。哈尔滨理工大学机械动力工程学院硕士研究生。焦艳,女,1990年生。哈尔滨理工大学机械动力工程学院硕士研究生。廉冲,女,1989年生。哈尔滨理工大学机械动力工程学院硕士研究生。
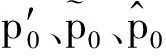
3 仿真与实验
3.1 仿真系统的开发

3.2 仿真实验与分析



3.3 实验验证与分析


4 结语
