致密油储层水平井体积压裂套管变形失效机理数值模拟研究

刘伟，陶长洲，万有余，池晓明，李扬，林海，邓金根

1 中国石油大学(北京)油气资源与工程国家重点实验室，北京 102249 2 中国石油大学(北京)石油工程学院，北京 102249 3 川庆钻探长庆井下技术作业公司，西安 710018 4 青海油田分公司钻采工艺研究院，敦煌 736202

致密油储层水平井体积压裂套管变形失效机理数值模拟研究

刘伟1,2*，陶长洲3，万有余4，池晓明3，李扬1,2，林海4，邓金根1,2

1 中国石油大学(北京)油气资源与工程国家重点实验室，北京 102249 2 中国石油大学(北京)石油工程学院，北京 102249 3 川庆钻探长庆井下技术作业公司，西安 710018 4 青海油田分公司钻采工艺研究院，敦煌 736202

本文对国内某致密油区块4口水平井体积压裂套管变形失效情况进行了统计分析，运用有限元方法对体积压裂过程中3类因素引起的套管变形规律进行了数值模拟。现场数据统计与数值分析结果表明：(1)该区块体积压裂套管缩径变形量较大，可达1～3 cm；(2)压裂引起的套管外挤力及其非均匀性增加可能导致套管屈服，但是缩径变形量较小，一般不超过3 mm；(3)压裂改造区域在套管两侧分布不对称可能导致套管发生整体弯曲变形，但套管横截面形状与尺寸几乎不变；(4)该区块水平地应力差较大，天然裂缝/小型断层容易剪切激活，裂缝面错动量可达3～5 cm，导致套管受强烈剪切而变形，缩径量达1 cm以上，且变形特点与铅印探测的套管变形特点吻合。综合现场数据统计与数值计算结果，认为与套管相交的天然裂缝/小型断层在压裂过程中激活与错动是引起目标致密油区块体积压裂套管变形失效的主要原因。本文研究结果可为体积压裂套管变形失效防治提供理论参考。

体积压裂；套管变形；水平井；天然裂缝；有限元分析

0 引言

体积压裂技术是近年来国内外为有效开发非常规油气藏而发展的一项新技术，广泛应用于致密砂岩、页岩等非常规油气储层的改造[1-3]。国内外压裂施工实践表明，体积压裂作业在实现储层有效改造的同时也可能带来套管变形失效问题。公开文献显示，国内青海油田致密油区块[4]、四川须家河致密气、川中侏罗系致密油、威远-长宁页岩气示范区等区块[5]的致密油气、页岩气储层体积压裂过程中均存在不少套管变形失效现象，导致桥塞、磨鞋下入困难，压裂作业无法按原计划顺利进行，严重影响开发进程，造成经济损失。

国内外研究人员针对这一问题已经开展了一些研究[6-12]。蒋可等人[7]分析了水泥环缺失、套管偏心等固井质量问题对页岩气水平井套管损坏的影响。于浩等人、Lian等人[5,8-9]通过数值模拟，认为压裂过程中套管损坏是改造区域内地层岩石性能降低、改造区域不对称、施工压力过大以及地应力场重新分布共同作用的结果。Shen等人[10-11]认为固井质量差与压裂改造区域不对称共同作用导致压裂过程中套管发生变形失效，提出控制施工压力以防治套损。Yan等人[12]对四川长宁威远地区页岩气套管损坏情况进行计算分析，认为水泥环孔隙压力降低可能是该地区套管损坏的主要原因。总体来看，目前对于体积压裂套管变形失效的机理尚未形成统一认识，对于套管变形失效的主要机理认识尚不清楚。此外，现场施工数据表明压裂过程中套管变形失效呈现缩径变形量大的特点，需要结合这一特点对体积压裂套管变形失效机理开展进一步深入研究。

本文针对国内某致密油区块4口水平井体积压裂过程中的套管变形失效问题开展研究。首先对现场套管实际变形失效情况进行了统计分析，在此基础上，运用有限元数值方法对该区块典型体积压裂施工过程中3类因素对套管变形的影响规律进行分析，探索该区块体积压裂过程中套管变形失效的主要机理，为体积压裂套管变形失效防治提供一定的理论参考。

1 国内某致密油区块体积压裂套管变形失效统计分析

国内某致密油区块位于西北地区，属于断层切割的断鼻构造。该构造目前具有NF-SS(正断层-走滑断层)特征应力状态，最大水平地应力和上覆岩层压力接近。该区块致密油储层垂深约为3 200～3 300 m，储层厚度约为20 m。

为探索致密油效益开发技术，近年来在该区块布置了X1、X2、X3和X4共4口水平井，采用射孔-桥塞联作方式进行分段多簇体积压裂。每一压裂段一般有2～3个射孔簇，簇间距约为20～30 m。压裂施工过程中，4口井均出现了不同程度套管变形失效，具体表现为压裂完某一段之后进行下一段压裂时，由于套管发生严重变形而导致桥塞或管柱无法顺利下入指定位置。以X1井为例，该井水平段采用P110套管，套管壁厚为10.54 mm，设计开展10段压裂。第3段压裂结束后，由于套管变形导致桥塞无法下入，第4和第5段采用砂塞方式完成压裂，剩余5段压裂施工未能完成。考虑到X1井的情况，X2-X4井采用了钢级更高的Q125套管并将套管壁厚增加至12.7 mm，同时在施工过程中注意平稳变化排量以避免压裂压力大起大落，然而施工过程中仍然发生了套管变形失效问题。

表1汇总了X1-X4井压裂过程中记录的套管变形失效数据，对此进行总结和分析，可以大致推断套管变形破坏的位置以及套管变形程度。以X1井第4段压裂为例：第4段压裂结束后，下114 mm磨鞋在3 394 m遇阻，ϕ73 mm喷嘴可通过，下ϕ100 mm通井规在3 959 m遇阻。考虑到套管原始内径为118.62 mm，大致可以估计该处套管缩径变形量大于18.62 mm而小于45.62 mm。利用这一方法，我们对X1-X4井套管变形情况进行了统计分析，见表1。表1的统计结果表明，X1-X4井体积压裂过程中，套管缩径变形量的下限值大约为1～3 cm，呈现出缩径量较大的特点。

X2井在3 805.70 m处套管变形后，通过下入铅印进行了套管变形情况探查。图1所示为铅印起出后的变形情况，从图中可以看到，铅印端面变为不规则椭圆形，呈现一侧发生变形而另一侧几乎没有变形的特点。

2 体积压裂套管变形失效影响因素分析

国内外已有研究与现场施工分析表明，体积压裂套管变形失效的潜在影响因素包括：(1)体积压裂改造区域内地应力场发生变化，套管外挤力及其非均匀程度增加；(2)大量压裂液进入地层，引起压裂改造区域孔隙压力增大，导致套管外挤力增大；(3)黏土遇水膨胀导致套管外挤力增大；(4)固井质量存在缺陷，放大套管外挤力的非均匀程度；(5)压裂改造区域在井筒两侧分布不对称；(6)体积压裂激活与井筒相交的天然裂缝或小型断层，使其发生剪切滑移。总的来看，影响因素(1)-(4)本质上都体现为套管外挤力及其非均匀程度增加，因此本文将因素(1)-(4)归纳为一类因素，从而将上述影响因素简化为3类：(a) 套管外挤力及其非均匀性增加，造成套管发生屈服与变形，示意图如图2(a) 所示；(b) 压裂改造区域在井筒两侧分布不对称，作用在套管两侧外挤力不均衡，造成套管弯曲变形，如图2(b)所示；(c) 压裂液进入地层后，与井筒相交的天然裂缝/小型断层内压力升高，摩擦力减小，裂缝/断层激活，发生滑移，使套管受剪切变形，如图2(c)所示。

本文基于有限元数值分析方法，利用ABAQUS通用非线性有限元软件，建立力学分析模型，开展上述3类因素对于体积压裂套管变形失效的影响规律分析，揭示该致密油区块体积压裂套管变形失效的主要机理。

通过室内三轴岩石力学实验与测井数据分析，得到如下基础参数：储层岩石弹性模量约为20 GPa，泊松比约为0.20，水泥弹性模量和泊松比分别为8 GPa和0.25。上覆岩层压力约为80 MPa，最大水平地应力约为82 MPa，最小水平地应力约为55 MPa，地层孔隙压力约为38 MPa，最大水平地应力方位在NE 30º～40°之间。

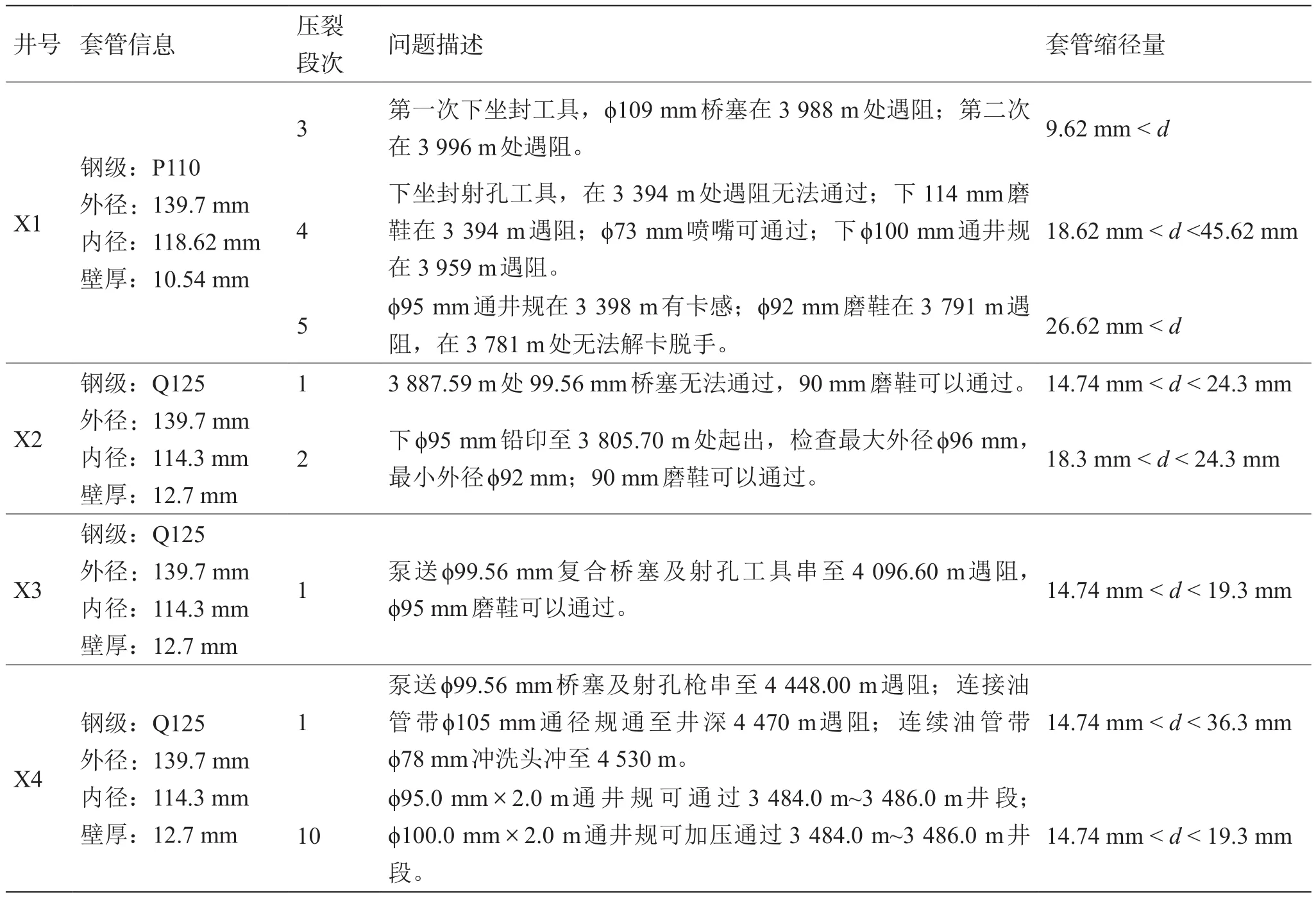
表1 国内某致密油区块4口水平井体积压裂套管变形概况Table 1 Descriptions of casing deformation during hydraulic fracturing of 4 horizontal wells in a tight-oil reservoir in China

图1 下入X2井3 805.70 m处的铅印变形情况Fig. 1 Deformation of the Lead Impression Block (LIB) run to 3 805.70 m of X2 well

2.1 套管外挤力及非均匀程度增加对套管变形失效的影响

体积压裂引起的近井筒区域应力场变化、孔隙压力变化、黏土吸水膨胀以及固井质量缺陷的影响可以归结为套管外挤力及其非均匀程度增加。为研究这一因素的影响，建立如图3所示套管-水泥环-地层组合体系二维平面应变模型，分别考虑完整水泥环和部分缺失水泥环的2种情况，开展套管受力与变形分析。

图3所示的计算模型整体尺寸为3 m×3 m，套管的内径和外径分别为114.3 mm和139.7 mm，水泥环的外径为215.9 mm。套管钢级为Q125，弹性模量和泊松比分别为210 GPa和0.3，屈服强度为864 MPa。考虑最小地应力σmin为50 MPa和 80 MPa两种情况，分析地应力差值(∆σ=σmax−σmin)逐渐从0 MPa增加到100 MPa条件下的套管受力与变形规律。压裂施工过程中停泵后，套管内压力下降，对此本文在计算中考虑了较为极端的工况，假设套管内部完全掏空，套管内表面无压力作用。此外，为反映固井质量的影响，计算过程中考虑了水泥环完整以及水泥环存在部分缺失两种情况，如图3的局部放大图所示。

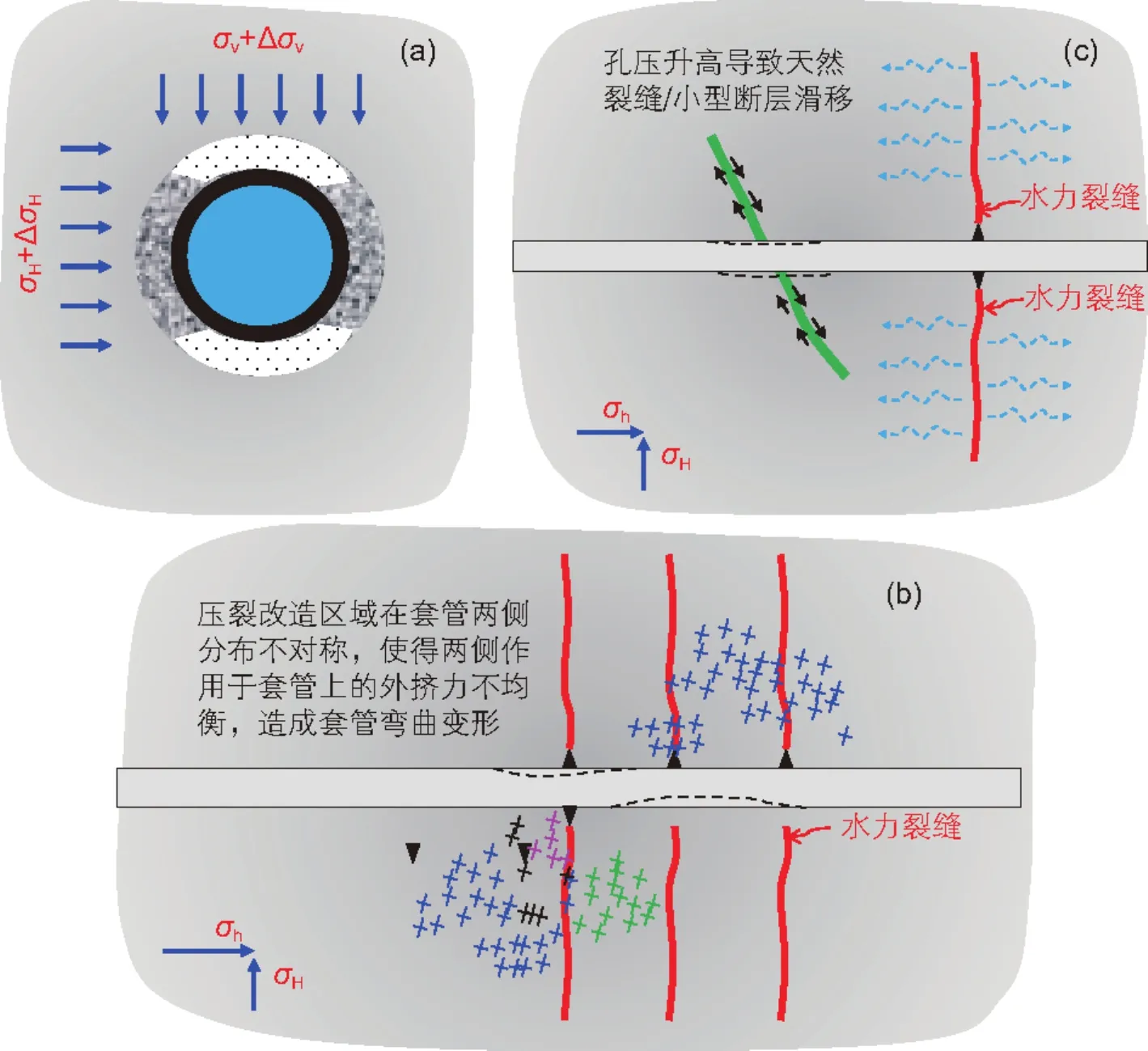
图2 体积压裂套管变形失效的3类影响因素：(a) 套管外挤力及其非均匀性增加；(b)压裂改造区域在套管两侧分布不对称；(c)天然裂缝/小型断层激活、滑移Fig. 2 Three factors influencing the casing deformation during hydraulic fracturing treatment: (a) amplified non-uniform loading on the casing; (b) asymmetric distribution of stimulated reservoir volume about the wellbore; (c) shear reactivation of pre-existing natural fractures and/or minor faults

图3 非均匀载荷作用下套管受力与变形计算模型Fig. 3 Schematic of the numerical model for analyzing the stresses and deformation of casing under non-uniform loading

图4给出了最小地应力为80 MPa、水泥环完整、地应力差值分别为0 MP，30 MP，60 MP，90 MPa条件下，套管-水泥环-地层组合系统的Mises应力分布情况。结果显示，随着地应力差值增大，套管中Mises应力的最大值增加。图4(d)中的结果表明，地应力差值增加到90 MPa，套管中的Mises应力约为817.9 MPa，未发生塑性屈服。

图5所示为最小地应力为80 MPa、水泥环存在部分缺失、地应力差值分别为0 MP，30 MP，60 MP，90 MPa条件下，套管-水泥环-地层组合系统的Mises应力分布情况。和图4相比，套管部分的Mises应力急剧增加，地应力差值达到30 MPa时，套管上最大Mises应力已超过屈服强度。上述计算结果表明，水泥环的缺失会放大套管载荷的非均匀性，可能使套管局部部位发生塑性屈服。

图4 套管-水泥环-地层组合体系Mises应力分布(水泥环完整，σmin = 80 MPa)Fig. 4 Distribution of Mises stress within the casing-cement-formation system (high-quality cement, σmin = 80 MPa)

图5 套管-水泥环-地层组合体系Mises应力分布(水泥环部分缺失，σmin = 80 MPa)Fig. 5 Distribution of Mises stress within the casing-cement-formation system (low-quality cement, σmin = 80 MPa)

目标致密油区块现场施工情况表明，体积压裂套管变形失效呈现缩径变形量大的特点，因此不能仅考察套管是否发生塑性屈服，需要分析套管在不同条件下的缩径变形量。图6所示为不同最小地应力与固井质量条件下套管缩径变形量随地应力差值变化的计算结果。从图6可以看出，总体上套管缩径变形量随着地应力差值增大而增加。水泥环完整的条件下，地应力差值达到100 MPa，套管缩径变形量不超过1 mm，水泥环缺失放大套管外挤力非均匀性的条件下，地应力差值达到100 MPa对应的套管缩径变形量也不超过3 mm。

上述计算分析中，考虑了体积压裂引起的地应力差值高达100 MPa、套管无内压以及最小应力方向水泥环缺失等较为极端的工况。从分析结果来看，体积压裂引起的近井区域地应力及非均匀程度增加可能导致套管发生局部塑性屈服，然而套管缩径变形量较小，远小于压裂施工中检测到的实际变形量，因此这一因素不是导致目标致密油区块压裂过程中套管变形失效的主要原因。

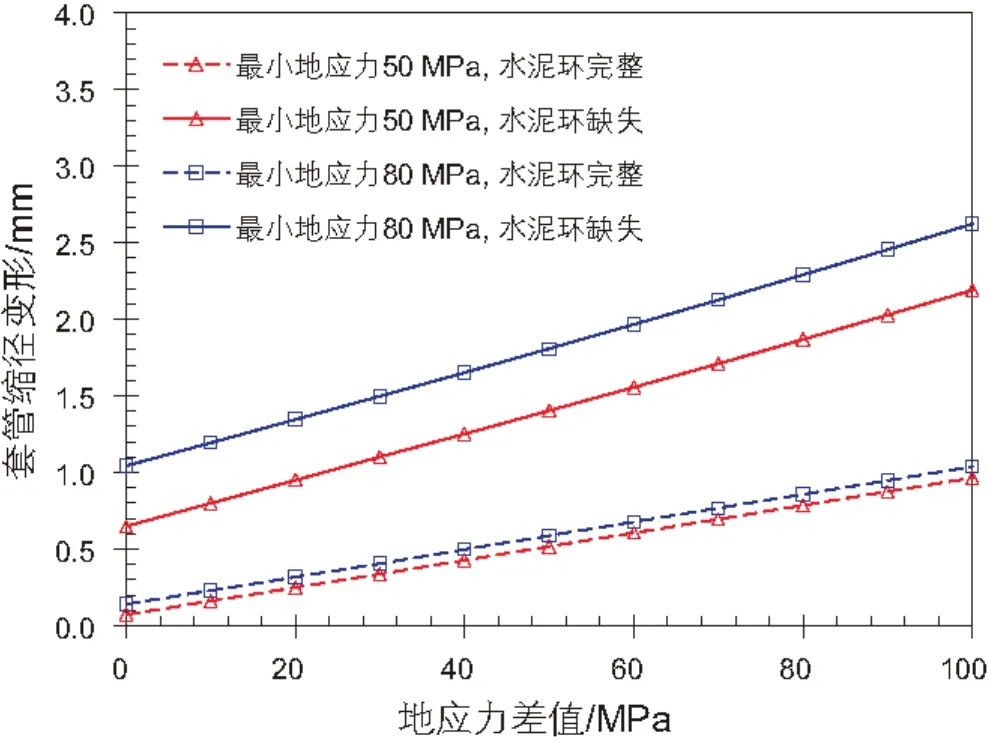
图6 套管缩径变形量随地应力差值的变化Fig. 6 Reduction of casing radius versus stress difference

2.2 压裂改造区域在套管两侧分布不对称对套管变形失效的影响

非常规储层体积压裂过程中，受天然裂缝、层理面的影响，压裂形成的水力裂缝往往不是简单的对称双翼缝，而是分布式裂缝网络。天然裂缝空间分布的非均匀性以及地应力与地层性质的非均质性导致体积压裂改造区域在井筒两侧的分布一般是非对称的。图7(a)所示为目标致密油区块X4井第1段压裂的微地震监测信号，显示微地震信号在井筒两侧分布明显不对称，反映出压裂改造区域在井筒两侧分布不对称。已有研究认为[8,10-11]，改造区域内岩石力学性质劣化、孔隙压力升高，将导致改造区域内地应力重分布，某些区域应力水平升高而另一些区域应力水平降低。这种压裂改造区域在套管两侧分布的不对称，将导致作用在套管两侧的推挤力不均衡，可能引起套管发生侧向弯曲变形以及截面形状和尺寸的变化。本文利用有限元方法对这一因素造成的套管受力变形规律进行分析。

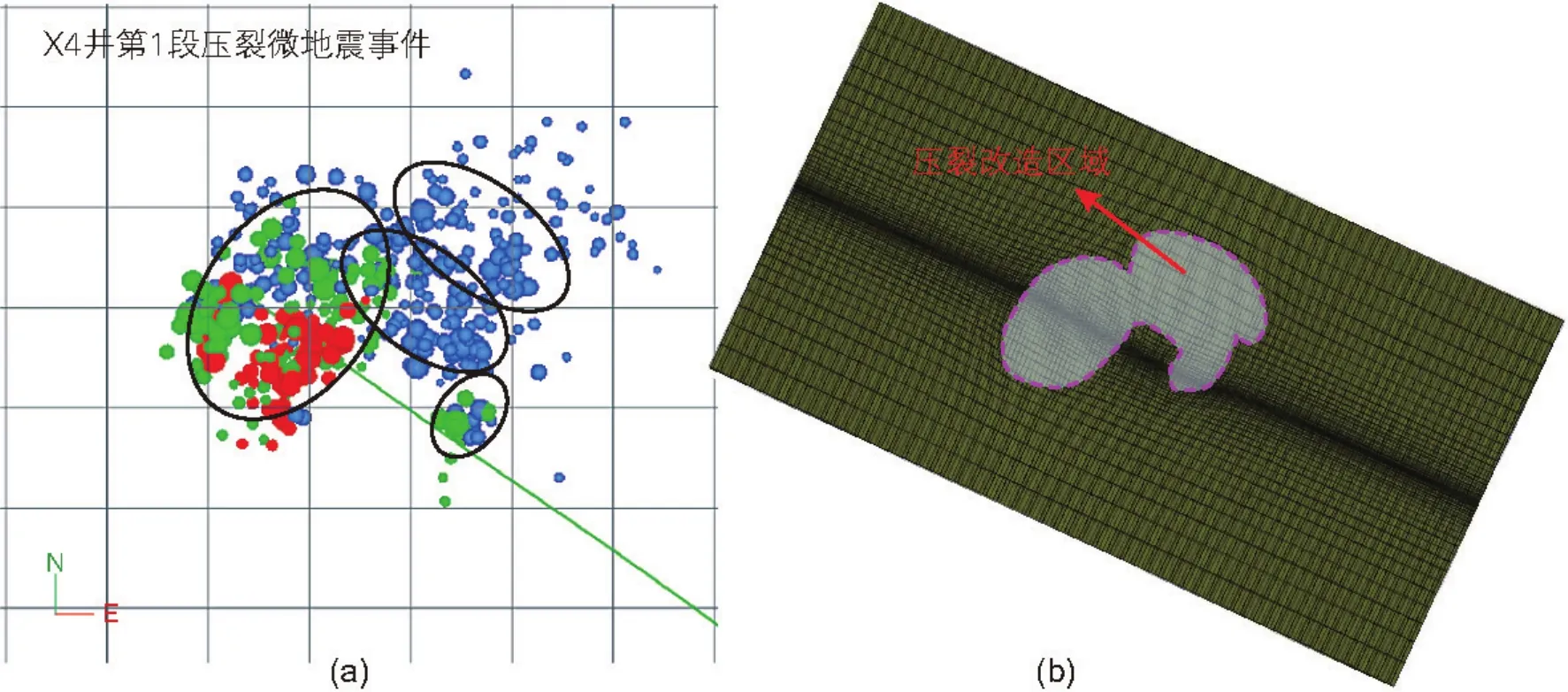
图7 (a)X4井第1段压裂微地震事件分布；(b)全局模型中的改造区域Fig. 7 (a) Map view of microseismic events during the first stage fracturing of X4 well; (b) stimulated reservoir volume in global model

X4井第1段压裂结束后，泵送桥塞至井深4 448 m遇阻，图7(a)显示该段压裂改造区域在井筒两侧分布不对称，因此以该段压裂为典型工况进行分析。计算过程中，利用文献[13-14]中常用的“子结构”方法分析套管的受力变形。具体思路与计算过程如图8所示。首先建立图8(a)所示尺寸为1 500 m×600 m×200 m的储层三维整体模型，分析压裂改造引起的储层应力重分布、储层岩石的变形以及套管的整体变形，随后建立如图8(b)所示尺寸为200 m×10 m×10 m的包含套管、水泥环、近井筒储层岩石的子模型，同时从全局模型的计算结果中提取得到子模型边界上的应力和位移作为边界条件，详细分析套管受力与变形的情况。全局模型中套管与水泥环组合体系简化为梁，采用三维梁单元进行描述，其等效截面面积、抗弯刚度等性质可由水泥环与套管的截面尺寸和材料参数进行估计。

全局模型中压裂改造区域的范围利用微地震监测结果进行估计，如图7(a)所示。同时参考文献[8,10]中的做法，认为改造区域内裂缝激活，岩石发生损伤，其等效弹性模量相比于损伤前岩石弹性模量会有一定程度的劣化，为此本文计算中利用ABAQUS软件二次开发功能USDFLD将图7(b)所示改造区域内的岩石弹性模量弱化为原始岩石地层弹性模量的10%。改造区域通过裂缝网络与井筒连通，认为其孔隙压力接近井筒内流体压力，结合施工数据，将改造区域内的孔隙压力设置为75 MPa，非改造区域则为原始孔隙压力38 MPa。计算过程中的其它参数如地应力、套管与水泥环的力学性质参数等与前文相同。

图9所示为全局模型计算得到的X4井第1段压裂过程中套管整体侧向位移分布。结果表明，体积压裂改造区域非对称使得压裂后作用在套管两侧的推挤力不平衡，导致套管在较大长度范围发生整体侧向位移与弯曲变形，最大侧向位移约为8 cm。图10所示为子模型计算所得X4井第1段压裂过程实测套损位置4 448 m附近的套管变形计算结果，显示套管侧向位移大约为7 cm左右，然而从图中所示套管弯曲变形比较集中的两个部位的放大图可以看到，套管仅发生整体侧向位移和弯曲变形，截面形状变化很小，提取相关计算结果表明截面缩径变形量仅为0.1～1.0 mm的量级。

上述针对X4井第1段压裂的典型工况计算与分析结果表明，压裂改造区域在套管两侧分布不对称，将引起套管整体发生侧向位移与弯曲变形，而套管变形部位的截面形状与尺寸变化非常小，远小于压裂施工中检测到的套管缩径变形量，因此认为这一因素也不是引起目标致密油区块体积压裂套管变形破坏的主要因素。

图8 压裂改造区域在套管两侧分布不对称引起套管变形失效分析:(a)全局模型；(b)子模型Fig. 8 (a) Global model and (b) sub-model for analyzing the casing deformation induced by asymmetric distribution of stimulated reservoir volume about the casing

图9 压裂改造区域在井筒两侧分布不对称导致的套管整体侧向变形Fig. 9 Overall deflection of casing induced by asymmetric distribution of stimulated reservoir volume with respect to the wellbore

2.3 与井筒相交的天然裂缝/小型断层滑移对套管变形失效的影响

体积压裂过程中，大量压裂液注入地层，导致天然裂缝面或断层面内压力升高、法向应力降低、裂缝面摩擦强度降低，原先在地下处于平衡状态的天然裂缝或断层可能被激活并发生错动，该现象在压裂微地震监测中已经得到证实[15]。当与井筒相交的天然裂缝/小型断层激活并错动时，将使套管受剪切变形。油气开采过程中超压注水、储层衰竭等因素引起地层弱面、断层滑移错动导致的套管变形破坏问题已经得到广泛的关注，经过多年的研究，已经取得了一定的研究成果和认识[16]，压裂过程中的天然裂缝/小型断层错动导致的套管变形则研究较少。本文利用有限元数值方法对于不同条件下的天然裂缝错动特征与规律、裂缝错动导致的套管变形程度与规律开展研究。

目标区块的地应力具有走滑断层特征，发育高角度天然裂缝，其剪切滑移主要与水平地应力差值、裂缝长度、裂缝方位(与最大水平地应力方位夹角)、以及压裂引起的缝内流体压力升高有关。建立如图11所示的天然裂缝剪切滑移分析平面应变模型，模型整体尺寸为400 m×400 m，裂缝长度l范围取5～50 m, 裂缝与最大水平地应力之间夹角θ取15°、30°和45°3种情况，裂缝面摩擦系数取为0.6。考虑两组地应力进行对比分析情况：(1)本文的目标致密油区块(σH= 82 MPa，σh= 55 MPa)，地应力差值为 27 MPa；(2)国内西北地区某致密砂岩气区块(σH= 60 MPa，σh= 50 MPa)，地应力差值为10 MPa。

图12所示为不同裂缝内流体压力、裂缝长度和裂缝方位条件下裂缝面中点处的错动量的计算结果。图12(a)-(c)是目标致密油区块较高差应力(27 MPa)条件下的错动量变化情况，图12(d)-(f)则是相对较低差应力(10 MPa)条件下的错动量变化情况。可以看出，总体上裂缝长度越长、缝内流体压力越高，天然裂缝错动量越大。对比来看，本文所考虑的致密油区块具有较高差应力，原始状态下天然裂缝/小型断层错动趋势较为强烈，压裂引起缝内流体压力升高，天然裂缝/小型断层比较容易发生激活、错动，且错动量较容易达到3～5 cm的量级；相比之下，较低应力差情况下，原始状态天然裂缝/小型断层的错动趋势较弱，激活后天然裂缝错动量相对较小，一般不超过2 cm。

图 10 子模型中套管位移(单位，m)Fig. 10 Displacement of casing in the sub-model (unit, m)

图11 天然裂缝滑移错动计算的模型示意图Fig. 11 Sketch of the model for analyzing the slippage of natural fracture

图 12 不同裂缝长度、缝内流体压力、裂缝方位条件下的天然裂缝滑移错动位移Fig. 12 Slippage of natural fracture for different length, pressure and direction conditions

为分析与井筒相交的天然裂缝/小型断层发生激活、错动导致的套管受力变形规律，建立如图13所示地层-水泥环-套管三维有限元模型，模型整体尺寸为10 m×10 m×60 m。水泥环和地层之间、套管与水泥环之间以及裂缝面之间设置摩擦接触，摩擦系数均为0.6。其余材料参数、地应力参数与前文计算中所用参数相同。利用该模型，对不同天然裂缝角度和裂缝错动量条件下的套管变形规律进行分析。

图14给出了天然裂缝/小型断层与最大水平地应力夹角为30°(井眼沿最小水平地应力方向钻进，因此裂缝与井筒夹角为60°)、裂缝面错动位移为5 cm情况下套管的变形情况。从图中所示结果来看，天然裂缝/小型断层发生错动时，套管会受到强烈的剪切作用，发生局部急剧缩径变形。该典型工况的计算结果表明，5 cm的裂缝错动位移导致的套管缩径量可达到2.28 cm。

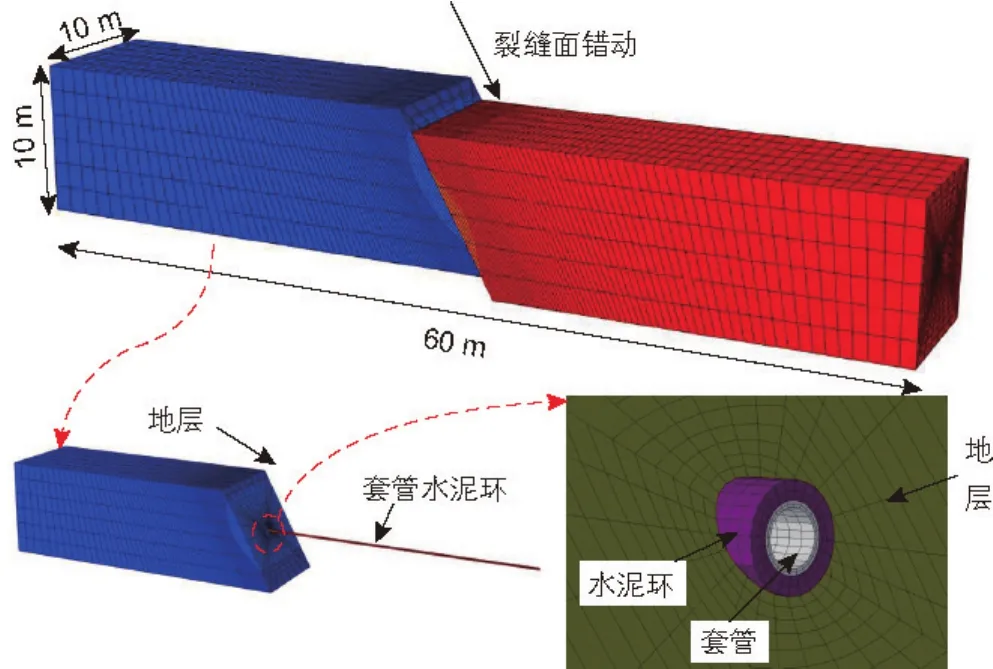
图13 天然裂缝/小型断层错动导致套管受力变形分析有限元模型Fig. 13 Finite element model for casing deformation analysis induced by natural fracture slippage

图15为目标致密油区块中不同天然裂缝/小型断层方向以及不同裂缝错动量条件下的套管缩径变形量。结果表明，总体上套管的缩径量随裂缝错动量的增大而增大。天然裂缝错动位移超过一定临界值(约2～3 cm)后，套管缩径量快速增大，3～4 cm的天然裂缝错动位移产生的套管缩径变形可到达1～2 cm，这一变形量级与目标致密油区块体积压裂施工中实际检测到的套管缩径量级一致。此外，仔细观察图14中的套管变形特点，可以发现套管在缩径变形处呈现出“一侧急剧变形、另一侧几乎保持平直”的特点，与图1中所示现场铅印端面“一侧发生变形而另一侧几乎没有变形”特点吻合。因此认为与套管相交的天然裂缝在压裂过程中发生错动是引起该致密油区块体积压裂过程中套管变形失效的主要原因。

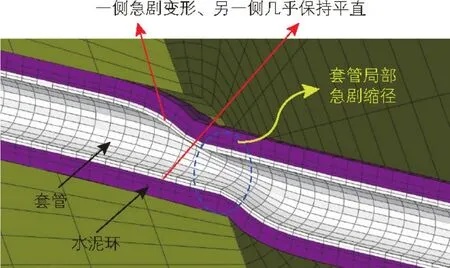
图14 天然裂缝/小型断层滑移错动导致套管变形的典型工况计算结果Fig. 14 Typical simulation results of the casing deformation induced by natural fracture slippage

3 结论

本文对国内某致密油区块水平井体积压裂套管变形失效的现场数据进行了统计分析，在此基础上运用有限元数值方法对该区块典型体积压裂施工过程中各类因素对套管变形的影响规律进行了分析，得到如下认识：

(1)目标致密油区块体积压裂过程中套管失效变形较大，缩径量可达1～3 cm。

(2)体积压裂引起套管外挤力及其非均匀性增加可能导致套管发生屈服，然而套管缩径变形量较小，一般不超过3 mm。体积压裂改造区域在套管两侧分布不对称可能导致套管发生整体侧向弯曲变形，然而套管横截面形状与尺寸几乎不变，缩径量较小。这两类因素导致的套管变形量都远小于压裂施工中检测到的套管实际变形量。

图15 不同天然裂缝/小型断层方向与错动位移条件下的套管缩径变形量Fig. 15 Reduction of casing radius for different directions and slippage of natural fractures

(3)该区块水平地应力差较大，压裂液进入天然裂缝或断层后容易使其激活并发生错动，裂缝面错动量可达到3～5 cm，导致的套管缩径量达1 cm以上，与实际套管缩径量级一致，且天然裂缝/断层错动导致的套管变形特点与铅印反映的套管实际变形特点吻合。

综合现场数据与数值模拟分析，认为与套管相交的天然裂缝在压裂过程中发生滑移是引起该致密油区块体积压裂过程中套管变形失效的主要原因。本文的研究结果可为该致密油区块及类似非常规储层体积压裂套管变形失效防治提供一定的参考。

[1] 曾凡辉, 郭建春, 刘恒, 等. 北美页岩气高效压裂经验及对中国的启示[J]. 西南石油大学学报(自然科学版), 2013, 35(6): 90-98.[ZENG F H, GUO J C, LIU H, et al. Experience of efficient fracturing of shale gas in North America and enlight enment to China[J].Journal of South-west Petroleum University(Science & Technology Edition), 2013, 35(6): 90-98.]

[2] 吴奇, 胥云, 王晓泉, 等. 非常规油气藏体积改造技术——内涵, 优化设计与实现[J]. 石油勘探与开发, 2012, 39(3): 352-358.[WU Q, XU Y, WANG X Q, et al. Volume fracturing technology of unconventional reservoirs: Connotation, design optimization and implementation[J]. Petroleum Exploration and Development, 2012, 39(3): 352-358.]

[3] 吴奇, 胥云, 王腾飞, 等. 增产改造理念的重大变革——体积改造技术概论[J]. 天然气工业, 2011, 31(04): 7-12.[WU Q, XU Y,WANG T F, et al. The revolution of reservoir stimulation: An introduction of volume fracturing[J]. Natural Gas Industry, 2011, 31(4):7-12.]

[4] 万有余, 郭子义, 林海, 等. 体积压裂在青海油田扎哈泉致密油中的应用[J]. 中国化工贸易, 2015, (9): 122-123. [WAN Y Y, GUO Z Y, LIN H, et al. Application of massive hydraulic fracturing in Zhahaquan tihgt-oil reservoir of Qinghai oil field[J]. China Chemical Trade, 2015, 9: 122-123.]

[5] 于浩. 体积压裂过程中套管失效机理研究[D]. 成都: 西南石油大学, 2015.[YU H. Investigation of casing failure mechanism during volumetric fracturing[D]. Chengdu:Southwest Petroleum University, 2015.]

[6] 田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J]. 天然气工业, 2015, 35(9): 70-76.[TIAN Z L, SHI L, QIAO L.Research of and countermeasure for wellbore integrity of shale gas horizontal well[J]. Natural Gas Industry, 2015, 35(9): 70-76.]

[7] 蒋可, 李黔, 陈远林, 等. 页岩气水平井固井质量对套管损坏的影响[J]. 天然气工业, 2015, 35(12): 77-82.[JIANG K, LI Q, CHEN Y L, et al. Influence of cementing quality on casing failures in horizontal shale gas wells[J]. Natural Gas Industry, 2015, 35(12): 77-82.]

[8] LIAN Z, YU H, LIN T, et al. A study on casing deformation failure during multi-stage hydraulic fracturing for the stimulated reservoir volume of horizontal shale wells[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 538-546.

[9] 于浩, 练章华, 林铁军. 页岩气压裂过程套管失效机理有限元分析[J]. 石油机械, 2014, 42(8): 84-88.[YU H, LIAN Z H, LIN T J.Finite element analysis of failure mechanism of casing during shale gas fracturing[J]. China Petroleum Machinery, 2014, 42(8): 84-88.]

[10] SHEN X, SHEN G, STANDIFIRD W. Numerical estimation of upper bound of injection pressure window with casing integrity under hydraulic fracturing[C]. 50th US Rock Mechanics/Geomechanics Symposium, Houston, Texas, USA, June 26-29, 2016.

[11] SHEN X. Numerical estimation of casing integrity under injection pressure for fracturing of shale gas formation [C]. Shale Energy Engineering, Pittsburgh, Pennsylvania, USA, July 21-23, 2014.

[12] YAN W, ZOU L, LI H, et al. Investigation of casing deformation during hydraulic fracturing in high geo-stress shale gas play[J]. Journal of Petroleum Science and Engineering, 2016, 150: 22-29.

[13] RIGHETTO G, LAUTENSCHLÄGER C, ALBUQUERQUE R, et al. A smart way to build geomechanical models and analyze casing collapse during the petroleum field development[C]. 48th US Rock Mechanics/Geomechanics Symposium, Minneapolis, Minnesota,USA, June 1-4, 2014.

[14] HILBERT JR L, GWINN R, MORONEY T, et al. Field-scale and wellbore modeling of compaction-induced casing failures[J]. SPE Drilling & Completion, 1999, 14(02): 92-101.

[15] ZOBACK M D, KOHLI A, DAS I, et al. The importance of slow slip on faults during hydraulic fracturing stimulation of shale gas reservoirs[C]. SPE Americas Unconventional Resources Conference, Pittsburgh, Pennsylvania, USA, June 5-7, 2012.

[16] DUSSEAULT M B, BRUNO M S, BARRERA J. Casing shear: causes, cases, cures[C]. SPE International Oil and Gas Conference and Exhibition in China, Beijing, China, November 2-6, 1998.

Numerical analysis of casing deformation during massive hydraulic fracturing of horizontal wells in a tight-oil reservoir

LIU Wei1,2, TAO Changzhou3, WAN Youyu4, CHI Xiaoming3, LI Yang1,2, LIN Hai4, DENG Jingen1,2
1 State Key Laboratory of Petroleum Resource & Engineering, China University of Petroleum-Beijing, Beijing 102249, China 2 College of Petroleum Engineering, China University of Petroleum-Beijing, Beijing 102249, China 3 Changqing Downhole Technology Treatment Company, Xi’an 710018, China 4 Research Institute of Drilling and Production, Qinghai Oilfield Company, Dunhuang 736202, China

Casing failures have been frequently encountered during multi-stage hydraulic fracturing of horizontal wells drilled in unconventional reservoirs, resulting in failure to install bridge plugs of subsequent stages to the design depths, or even abandonment of all the remaining fracturing stages. In this paper, we performed an integrated study of casing failures during the fracturing of four horizontal wells drilled in a tight-oil reservoir in Northwest China, by analyzing the field data as well as numerically investigating the influence of various factors on the casing deformation. The results show that: (1) fracturing induced casing failures in this reservoir feature excessive localized radial deformation, and the reduction of diameter generally amounts to 1～3 cm; (2) fracturing-induced non-uniform loading on the casing together with a poor cement sheath may lead to localized yielding, while the reduction of diameter is small, generally not more than 3 mm; (3) asymmetric distribution of the stimulated reservoir volume with respect to the wellbore can cause overall bending deformation of the casing, however, the cross-sectional shape and size does not change noticeably; (4) the high contrast between the two in-situ horizontal principal stresses in this reservoir makes shear activation of pre-existing fractures or faults during the fracturing highly possible, which can deform the casing severely if the pre-existing fracture or fault intersect the casing, resulting in a reduction of diameter larger than 1 cm.By comparison of modeling-obtained deformation magnitude with the field-data, it is concluded that casing impairment during the hydraulic fracturing in this tight-oil reservoir is mainly due to the slip of pre-existing fractures/faults activated during the fracturing. Insights obtained in this study can be helpful for mitigating casing impairments during future fracturing jobs in similar unconventional reservoirs.

massive hydraulic fracturing; casing impairment; horizontal wells; shear slippage of pre-existing fracturing; finite element modeling

*通信作者, liuwei@cup.edu.cn

2017-02-08

刘伟, 陶长洲, 万有余, 池晓明, 李扬, 林海, 邓金根. 致密油储层水平井体积压裂套管变形失效机理数值模拟研究. 石油科学通报, 2017, 04: 466-477

LIU Wei, TAO Changzhou, WAN Youyu, CHI Xiaoming, LI Yang, LIN Hai, DENG Jingen. Numerical analysis of casing deformation during massive hydraulic fracturing of horizontal wells in a tight-oil reservoir. Petroleum Science Bulletin, 2017, 04: 466-477.doi:10.3969/j.issn.2096-1693.2017.04.043

10.3969/j.issn.2096-1693.2017.04.043

(编辑 马桂霞)