致密地层井壁失稳的孔隙弹性动力学机理研究

滕学清，陈勉，金衍，卢运虎*，夏阳1 中国石油大学(北京)石油工程学院，北京 1049 油气资源与探测国家重点实验室，北京 1049 中国石油塔里木油田公司，库尔勒 841000

致密地层井壁失稳的孔隙弹性动力学机理研究

滕学清1,2,3，陈勉1,2，金衍1,2，卢运虎1,2*，夏阳1,2
1 中国石油大学(北京)石油工程学院，北京 102249 2 油气资源与探测国家重点实验室，北京 102249 3 中国石油塔里木油田公司，库尔勒 841000

传统井壁失稳力学机制研究主要采用弹塑性静力学和孔隙弹性模型，忽略了井眼钻开瞬间引起的孔隙弹性动力学效应，无法解释超低渗透地层井壁围岩破坏的本质。本文基于Biot多孔介质弹性动力学理论，建立了多孔弹性地层各向异性应力场中井壁瞬时失稳力学模型，借助傅里叶变换将二维非均匀地应力场控制方程组分解为两个一维问题，分析了数值求解的收敛条件，模拟了井壁瞬时破坏动态演化过程及多孔弹性无因次参数对瞬时破坏的影响。研究表明，新模型计算出的井周孔隙压力场、有效应力场及切向与径向的有效应力差比经典孔隙弹性力学解大，在最小地应力方位井壁围岩易发生剪切破坏且破坏区域随时间增大，岩石孔隙流体饱和度对井壁瞬时失稳影响最大，饱和流体越多，井壁围岩失稳风险越高。本文所建立的孔隙弹性动力学模型为井壁失稳机理分析、井筒液柱压力设计提供了科学基础，并对超低渗透致密储层井壁失稳控制具有重要的工程意义。

多孔弹性；动力学；井壁失稳；致密地层

致密地层井壁失稳是迄今尚未得到有效解决的钻井复杂问题。从力学角度来讲，井壁失稳的诱因在于井眼凿开后井周产生应力集中，井筒内液柱压力未能与地层应力建立新的平衡，这种应力平衡受钻井液密度、性能、钻井工艺及地质条件等因素的影响。从时间尺度来讲，井壁稳定的力学模型分为小尺度的多孔弹性动力学模型、中等尺度的多孔弹性力学模型和大尺度的弹塑性静力学模型，国内外学者主要采用弹塑性静力学和孔隙弹性模型来研究井壁失稳的力学机制。弹塑性力学模型基于连续机制和小变形假设，结合平衡方程、几何方程、本构方程，根据相应边值问题，采用位移法、应力法求解位移场与应力场[13]，忽略了多孔介质中的流体运移及变形，认为受力体系任一微元都处于静力学平衡，应力、应变和位移只是空间坐标的函数，与时间无关，其给出的应力解可看作井眼凿开一定时间后的“平衡解”，由于求解方便，该力学模型在井壁稳定的力学研究中得到广泛应用[4-7]。孔隙弹性模型是基于Biot理论和多孔介质理论而建立的。1941年Biot提出多孔弹性力学理论[8]，而后Detournay& Chen将多孔弹性力学引入井壁稳定力学分析，推导出了各向异性地应力场中井周多孔弹性应力解与孔隙压力解[9]。而后众多学者结合井壁失稳工程情况进一步发展了多孔弹性力学，例如耦合钻井液溶质扩散[10-13]、耦合温度场[14-17]、考虑含天然裂隙的双重介质模型[18-19]及大斜度井井壁稳定性模型[20-21]，并获得井眼破坏的临界条件及动态演化过程。孔隙弹性力学模型计算出的井周应力场和孔隙压力场随时间和空间位置发生变化，孔隙压力在井壁内部达到最大值，且井壁围岩的破坏发生在近井壁处[22-23]。经过多年发展，孔隙弹性力学模型已经较为成熟，其给出的应力解可看作达到“平衡解”前流固耦合的一个动态演化过程，但孔隙弹性力学模型忽略了井眼打开瞬间井周应力扰动过程，无法揭示应力波动现象。

对于致密地层钻井而言，特别是高应力条件下井眼凿开瞬间井周应力分布实际上是一个应力扰动的问题，应力扰动的传播会形成弹性波，应力波动时常会引起井壁围岩的瞬时破坏，此时的力学行为属于弹性动力学研究范畴[24]。弹性动力学在地震勘探领域应用十分成熟，但在井壁失稳力学模型中应用较少，并且常规弹性动力学未考虑流体作用，不能应用于饱和流体的多孔弹性体应力瞬时扰动问题的研究。Biot基于孔隙弹性力学研究了弹性波在多孔弹性体中的传播[25-27]，计算出无旋波和等容波在介质中的传播速度，但并未给出位移和应力随时间的变化规律。Senjuntichai & Rajapakse采用势函数法得到了轴对称条件下井周瞬时应力解[28]，但目前几乎还没有关于非均匀应力场中考虑弹性波的井周应力解[29]。本文在Biot波动理论的基础上，系统分析非均匀地应力场中井眼凿开瞬间载荷变化和对应边界条件，将二维非轴对称问题分解为一维轴对称和非轴对称两部分进行求解，建立模型的数值求解方法，通过数值模拟，获得井周应力、孔隙压力随时间的动态变化规律，结合D-P准则，建立基于孔隙弹性动力学的井壁失稳预测模型，分析多孔弹性参数对井壁瞬时失稳的影响规律，为复杂地层钻井液密度设计提供理论依据。

1 基本控制方程

本文模型基于以下假设：

1)岩石是连续介质体，忽略裂缝、层理带来的非连续性；

2)岩石是均匀且各向同性的；

3)小变形，且变形处于线弹性状态。

岩石应力、孔隙压力与应变之间的关系为：

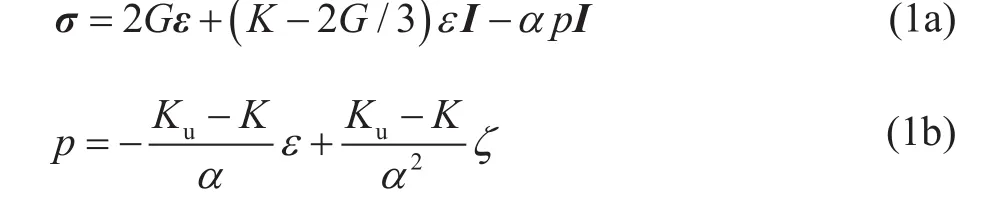
其中σ为应力张量，MPa ，以拉为正；ε为应变张量；ε为体积形变。K,G为体积模量和剪切模量，GPa；α为Biot系数，通常情况下α=1−K/Ks；p为孔隙压力，MPa；ζ为单位多孔介质的流体体积增量；Ku,Ks,K分别为不排水多孔介质、固体颗粒、排水多孔介质体积模量，GPa。Ku可由下式计算：

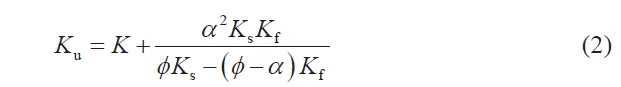
其中Kf为流体体积模量，φ为多孔介质孔隙度。岩石和流体的运动方程如下所示：

其中ρ为饱和多孔介质质量密度，且ρ= (1 −φ)ρs+φρf，ρf为流体密度，g/cm3；ρs为固体颗粒密度，g/cm3；q为流体流速矢量，cm/s；κ为孔隙介质渗透率，mD；η为流体黏度，mPa⋅s；a为表征流体附加质量的参数。将(2)式代入(3)式可得到岩石和流体在直角坐标系下的控制方程组：

式中各参数为无因次量，其中位移以井筒半径rw为单位，时间以rw为单位，其它无因次参数为

2 模型分解

初始应力场与孔隙压力场可表示为：

偏应力，σH为最大水平地应力，σh为最小水平地应力，为初始无因次孔隙压力。

井眼钻开瞬间，井筒处的边界条件为：

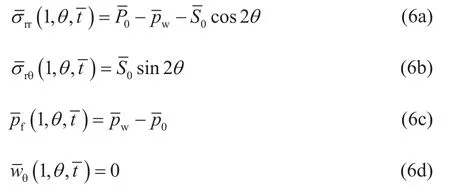
可将位移展开为傅里叶级数并仅保留2θ的正弦或余弦项，如下形式：

此时位移的解可看作傅里叶级数展开保留常数项与2θ余弦(或正弦)项之和，其中常数项代表了轴对称问题的解，而2θ余弦(或正弦)项代表了非轴对称问题的解。在轴对称问题中，不存在切向位移，因此切向位移中不存在常数项，仅在非轴对称问题中出现。将式(7)代入控制方程(4)中可得轴对称问题的控制方程为：

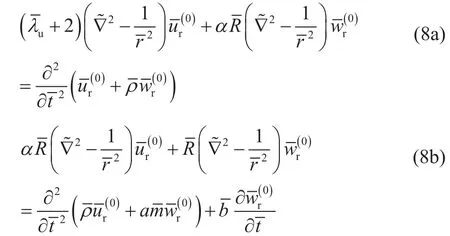
非轴对称问题的控制方程为：

经过模型分解，原二维问题变成了2个一维问题，数值求解难度降低。

3 数值模拟

轴对称模式与非轴对称模式控制方程均含有惯性项与黏滞项，因此方程是具有耗散项的波动方程，数值求解前需要对方程收敛性进行分析。本文基于MATLAB编程环境，对偏微分方程进行数值求解。在轴对称问题中，仅存在固体和流体的径向位移2个待求解变量，井筒处边界条件为定井底压力与径向应力。在非轴对称问题中，存在固体和流体的径向、切向位移4个待求解变量，井筒处边界条件为定井底压力、径向应力与切应力，以及井筒流体无旋，满足方程组的封闭性。实际地层参数取值见表1。

由于Senjuntichai & Rajapakse给出了轴对称问题的解析解，本文首先利用表1数据计算井壁处的固体、流体径向位移，并与Senjuntichai & Rajapakse给出的Laplace空间解析解进行对比，图1显示解的精确度较高，与解析解吻合度高。

4 结果及讨论

4.1 孔隙压力分布

分析了无因次时间为0.5，1.5，10时井周孔隙压力分布云图(图2)，图中的值表示孔隙压力与初始孔隙压力的比值，θ=0代表最小地应力方向。研究发现，井眼凿开瞬间在最大地应力方向井周形成低孔隙压力“环”，与初始状态相比，孔隙压力下降了50%以上；在最小水平地应力方向孔隙压力升高，主要是由于井壁围岩瞬间卸载，偏应力的存在使得最小地应力受压明显，引起局部孔隙压力升高，短时间内孔隙压力受围岩变形影响，流体扩散作用不明显。随着时间增加，受流体扩散作用影响，最小地应力方向孔隙压力先增大后减小，但始终高于原始孔隙压力，最大水平地应力方向孔隙压力逐渐恢复并趋于原始孔隙压力(图2(c))。最大(最小)孔隙压力在井壁内，且该位置随着时间不断向储层内部移动(图2(d))。显然孔隙压力这一短暂的变化过程对有效应力的影响不可忽略。

图3对比了相同时刻基于孔隙弹性力学计算的井周孔隙压力与基于孔隙弹性动力学计算的孔隙压力分布差异，结果显示加入流固惯性项后井周孔隙压力明显增大，特别在最小地应力方向，这使得井壁更易失稳。

4.2 应力分布

分析了径向有效应力与切向有效应力随时间的演化(图4和5)。在井眼凿开初期，井壁围岩瞬间卸载，引起井壁径向应力迅速降至井底压力，图4(a)中显示在最小地应力方向井壁内部存在一个低应力区，且该低应力区迅速向储层内部“传播”，而最大地应力方向径向应力较初始状态也明显减小，经过短暂的变化，当t>5时应力变化变得缓慢(图4(c)、(d))。图5所示井眼凿开后最小地应力方向有效切向应力逐渐变大，井壁处切向应力增大十分明显，例如在最小地应力方向原始切向有效应力为22 MPa，井眼形成后井壁处最大切向应力可达到55 MPa，可瞬间增大1倍，极易造成井壁的瞬时失稳。

表1 数值模拟参数取值Table 1 Values of parameters in the simulator

图1 本文数值计算结果(轴对称问题)与解析解对比：井壁处 (a) 固体径向位移；(b) 流体径向位移Fig. 1 Comparable results between numerical and analytical methods at the wellbore surface: (a) radial displacement of solid;(b) radial displacement of fluid

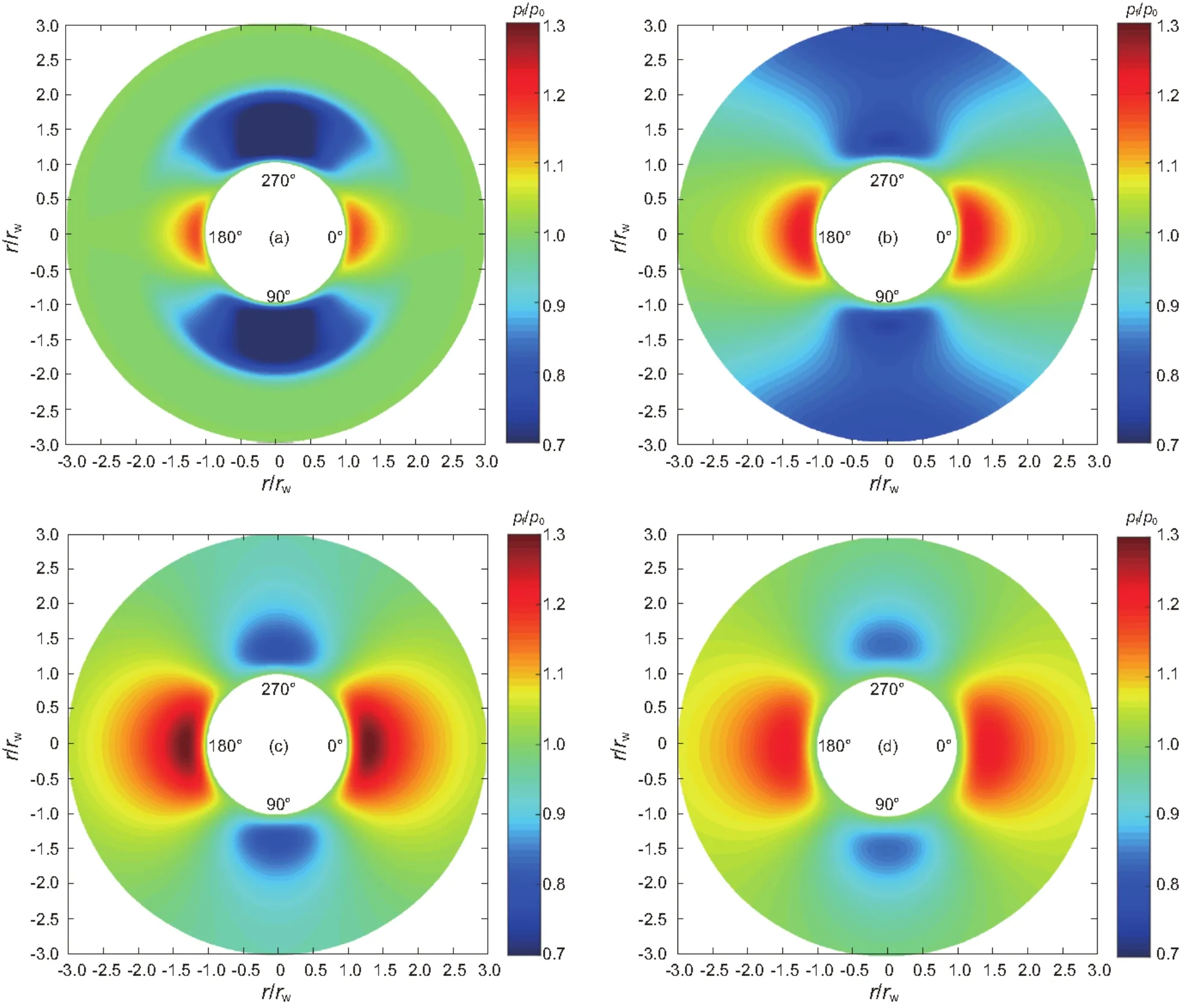
图2 井周孔隙压力随时间的变化：(a)=0.5; (b)=1; (c)=5; (d)=10Fig. 2 Distributions of pore pressure near the borehole at different times: (a)=0.5; (b)=1; (c)=5; (d)=10

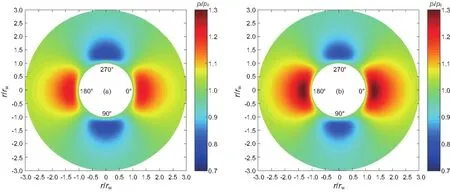
图3 井周孔隙压力在=2时分布规律对比：(a) 孔隙弹性力学解 (Detournay & Chen (1988))；(b) 孔隙弹性动力学解Fig. 3 Distributions of pore pressure near the borehole at =2: (a) poroelastodynamic solution; (b) poroelastic solution

图6和图7分别对比了采用孔隙弹性力学与孔隙弹性动力学模型得到的井周径向有效应力和切向有效应力。研究发现，在最小地应力方向，采用孔隙弹性力学模型，计算出的径向有效应力大于孔隙弹性动力学模型计算结果(特别是最小地应力方向靠近井壁处)，而切向有效应力小于孔隙弹性动力学模型计算结果。由此可知，采用孔隙弹性动力学模型获得的井周差应力 (切向应力与径向应力之差) 更大，井壁围岩更容易发生破坏。

4.3 井壁瞬时失稳分析

本文基于平面应变假设，轴向无位移，但轴向有效应力由下式给出：

其中σzz为轴向有效应力，σv为上覆应力，ν为泊松比，α为Biot系数。本文采用D-P准则[30][31]分析井壁瞬时失稳动态演化过程，表示如下：

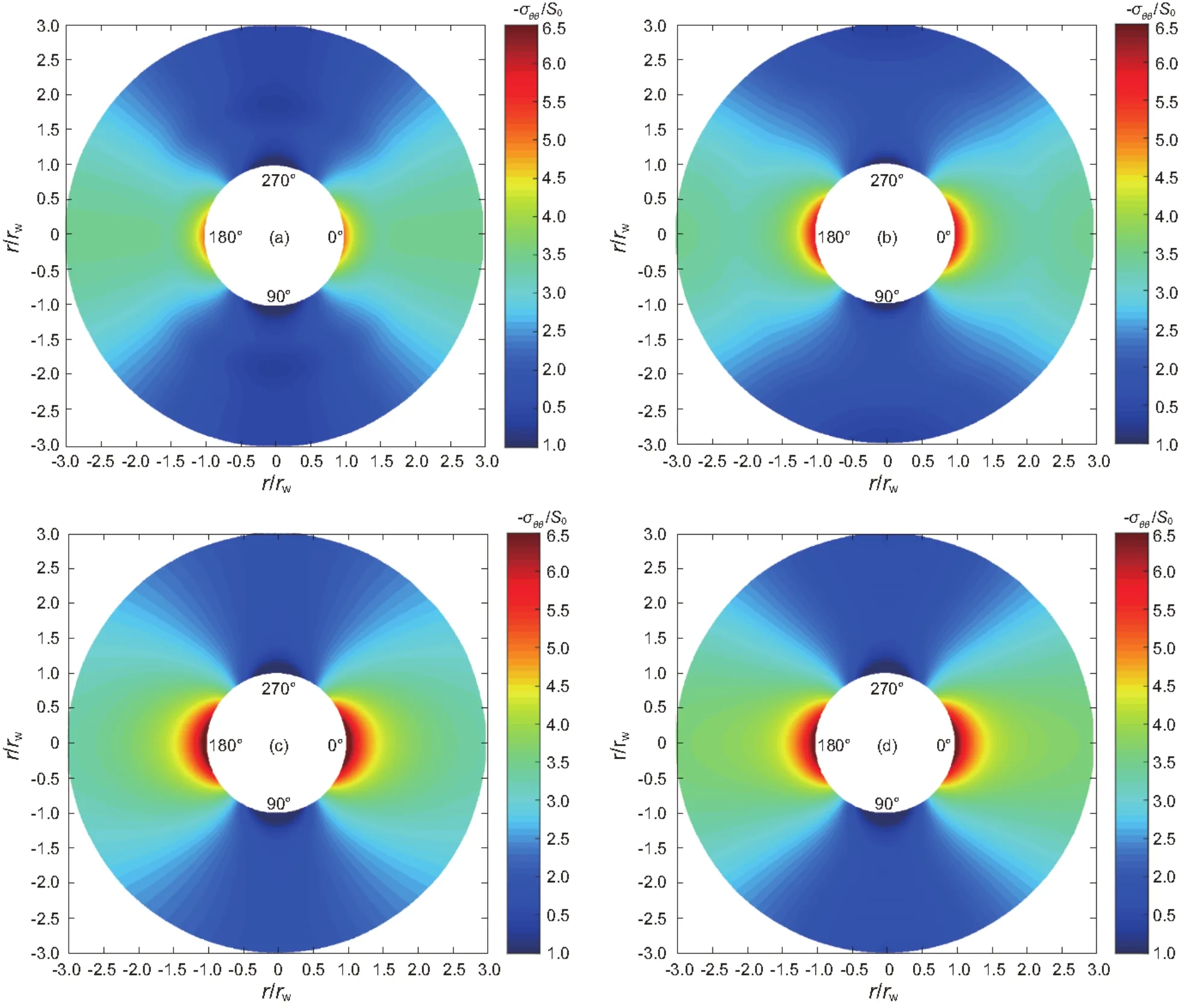
图5 井周有效切向应力随时间的变化：(a)=0.5; (b)=1; (c)=5; (d)=10Fig. 5 Distributions of effective hoop stress near the borehole at different times: (a)=0.5; (b)=1; (c)=5; (d)=10

图6 井周径向有效应力在=2时分布规律对比：(a) 孔隙弹性力学解 (Detournay & Chen (1988)); (b) 孔隙弹性动力学解Fig. 6 Distributions of effective radial stress near the borehole at=2: (a) poroelastodynamic solution; (b) poroelastic solution

图7 井周切向有效应力在=2时分布规律对比：(a) 孔隙弹性力学解 (Detournay & Chen (1988)); (b) 孔隙弹性动力学解Fig. 7 Distributions of effective hoop stress near the borehole at=2: (a) poroelastodynamic solution; (b) poroelastic solution

图8 井壁瞬时失稳过程 (F >0代表岩石已发生剪切破坏)：(a)=1; (b)=5Fig. 8 Transient failure of the wellbore (F >0 represents a shear failure): (a)=1; (b)5

其中A与D为材料常数，本文分别取值为A=0.1,D=15 MPa[17]，为平均剪应力，Sp为平均压应力，与Sp由下式计算：

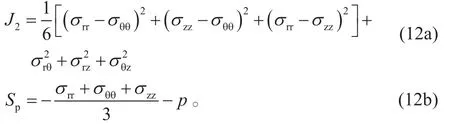
若令F=−3ASp+D为剪切破坏指数，可知当F>0时岩石发生剪切破坏，F越大代表越危险，岩石越容易发生剪切破坏。计算了井周剪切破坏指数的分布随时间的变化，结果如图8所示，在最小地应力方向井壁易失稳，这是由于最小地应力方向差应力最大，且破坏区域随着时间增长而增大，呈现动态破坏过程。

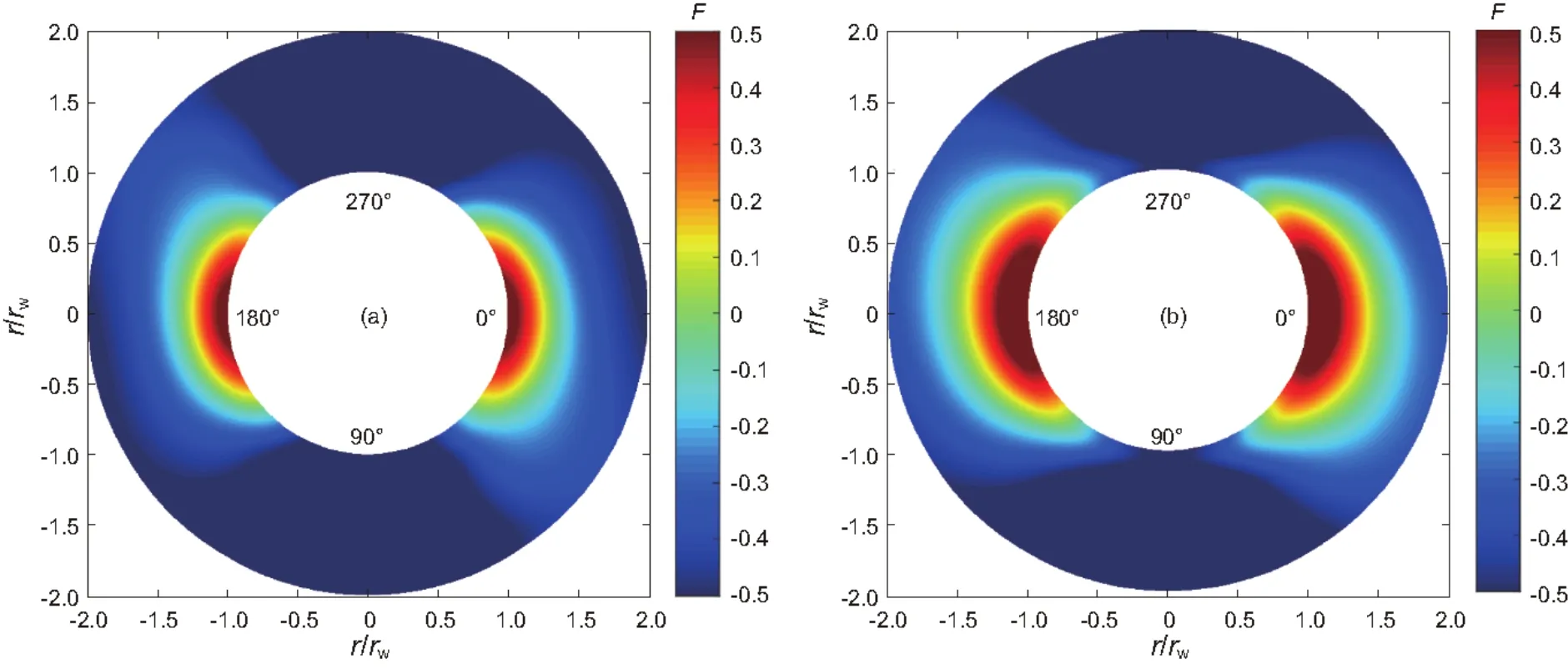
图9 多孔弹性无因次参数对井壁瞬时失稳的影响(a)=10; (b)=100Fig. 9 Effect of dimensionless poroelastic parameter on the transient failure of the wellbore: (a)=10; (b)=100

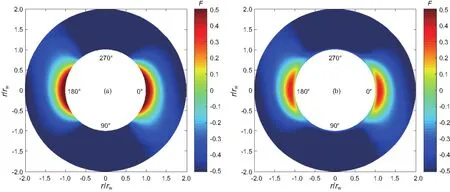
图10 多孔弹性参数α对井壁瞬时失稳的影响：(a)α=0.5; (b)α=0.8Fig. 10 Effect of dimensionless poroelastic parameter α on the transient failure of the wellbore: (a)α=0.5; (b)α=0.8

图11 多孔弹性无因次参数对井壁瞬时失稳的影响：(a)=100; (b)=1 000Fig. 11 Effect of dimensionless poroelastic parameteron the transient failure of the wellbore: (a)=100; (b)=1 000

分析了3个无因次多孔弹性参数对井壁瞬时失稳的影响：,α,，其中代表了多孔介质饱和流体量，当为0时，代表介质未饱和流体，当→∞，代表多孔介质完全饱和流体且流体不可压缩。α可看作单位体积多孔介质受挤压时排出流体体积，α越小代表多孔介质越易变形。例如，土体介质α值显著小于岩石介质α值。无因次参数常作为衡量多孔介质渗透率的参数，储层渗透率越大，参数越小。由计算结果可知，无因次参数对井壁瞬时失稳影响最大，即地层流体饱和度越大(或流体越不易压缩)，则井壁越易失稳且破坏面积越大；无因次参数α越小，井壁越易瞬时失稳；无因次参数b越大，即储层渗透率越小，井壁越易瞬时失稳。

5 结论

本文基于Biot饱和多孔介质弹性动力学理论，考虑孔隙流体、固体颗粒的压缩性及惯性、黏滞耦合作用建立了多孔弹性地层非均匀应力场井壁瞬时失稳动力学模型，研究了多孔弹性参数对井壁稳定瞬时失稳的影响规律，获得如下结论：

(1)井眼凿开瞬间，在最大地应力方向井周形成低孔隙压力“环”，在最小水平地应力方位孔隙压力升高；随着时间增加，受流体扩散作用影响，最小地应力方向孔隙压力先增大后减小，但始终高于原始孔隙压力，最大水平地应力方向孔隙压力逐渐恢复并趋于原始孔隙压力。

(2)在井眼凿开瞬间，在最小水平地应力方向，井壁径向应力迅速降至井底压力，井壁围岩内部存在低应力区且向内部移动，有效切向应力逐渐增大；而最大地应力方向，径向应力较初始状态也明显减小。

(3)相同时刻下，在最小地应力方向，采用孔隙弹性力学模型，计算出的径向有效应力大于孔隙弹性动力学模型计算结果(特别是最小地应力方向靠近井壁处)，而切向有效应力小于孔隙弹性动力学模型计算结果。由此可见，采用孔隙弹性动力学模型获得的井周差应力 (切向应力与径向应力之差) 更大，井壁围岩更容易发生破坏。

(4)井壁瞬时失稳动态过程显示破坏区域随时间不断增大，多孔岩石流体饱和度对井壁瞬时失稳影响最大。流体饱和度越高，井壁越易失稳，尤其是高应力超低渗透致密储层井壁围岩稳定性应考虑孔隙弹性动力学问题。

[1] 杨桂通. 弹塑性力学引论[M]. 北京: 清华大学出版社, 2004 [YANG G T. Introduction to elasticity and plasticity[M]. Beijing:Tsinghua University Press, 2004.]

[2] 陈勉, 金衍, 张广清. 石油工程岩石力学[M]. 北京: 科学出版社, 2008 [CHEN M, JIN Y, ZHANG G Q. Petroleum engineering rock mechanics[M]. Beijing: Science Press, 2008.]

[3] 金衍, 陈勉. 井壁稳定力学[M]. 北京: 科学出版社, 2012 [JIN Y, CHEN M. Wellbore stability mechanics[M]. Beijing: Science Press,2012.]

[4] 温航, 陈勉, 金衍, 等. 硬脆性泥页岩斜井段井壁稳定力化耦合研究. 石油勘探与开发, 2014, 41(6): 748-754 [WEN H, CHEN M, JIN Y, et al. A chemo-mechanical coupling model of deviated borehole stability in hard brittle shale[J]. Petroleum Exploration and Development, 2014, 41(6): 748-754.]

[5] 金衍, 齐自立, 陈勉, 等. 水平井试油过程裂缝性储层失稳机理. 石油学报, 2011, 32(2): 295-298 [JIN Y, QI Z L, CHEN M, et al. A mechanism study on the fractured reservoir instability during well testing of horizontal wells[J]. Acta Petrolei Sinica, 2011, 32(2): 295-298.]

[6] 陈勉, 赵海峰, 金衍, 等. 非连续介质力学模型预测煤层井眼稳定性. 石油学报, 2013, 34(1): 145-150 [CHEN M, ZHAO H F, JIN Y, et al. A discontinuous medium mechanical model for the sidewall stability prediction of coal beds[J]. Acta Petrolei Sinica, 2013,34(1): 145-150.]

[7] 卢运虎, 陈勉, 袁建波, 等. 各向异性地层中斜井井壁失稳机理. 石油学报, 2013, 34(3): 563-568 [LU Y H, CHEN M, YUAN J B,et al. Borehole instability mechanism of a deviated well in anisotropic formations[J]. Acta Petrolei Sinica, 2013, 34(3): 563-568.]

[8] BIOT. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12: 155-164.

[9] DETOURNAY E, CHENG A H D. Poroelastic response of a borehole in a non-hydrostatic stress field[J]. International Journal of Rock Mechanics and Mining Sciences, 1988, 25: 171-182.

[10] HUYGHE J M, JASSEN J D. Thermo-chemo-electro-mechanical formulation of saturated charged porous solids[J]. Transport in Porous Media, 1999, 34: 129-141.

[11] NGUYEN V X, ABOUSLEIMAN Y N. Incorporating electrokinetic effects in the porochemoelastic inclined wellbore formulation and solution[J]. Anais da Academia Brasileira de Ciências, 2010, 82: 1-28.

[12] TRAN M H, ABOUSLEIMAN Y N. Anisotropic porochemoelectroelastic solution for an inclined wellbore drilled in shale-Special Issue Olivier Coussy[J]. Journal of Applied Mechanics, 2013, 80: 020 912.

[13] NGUYEN V X, ABOUSLEIMAN Y N, HOANG S K. Analyses of wellbore instability in drilling through chemically active fractured rock formations[J]. SPE Journal, 2009, 14: 283-301.

[14] CHEN G, CHENEVERT M E, SHARMA M M, et al. A study of wellbore stability in shales including poroelastic, chemical, and thermal effects[J]. Journal of Petroleum Science and Engineering, 2003, 38: 167-176.

[15] WANG Y, DUSSEAULT M B. A coupled conductive-convective thermos-poroelastic solution and implications for wellbore stability[J].Journal of Petroleum Science and Engineering, 2003, 38: 187-198.

[16] YU M, CHEN G, CHENEVERT M E, et al. Chemical and thermal effects on wellbore stability of shale formations. In: SPE Annual Technical Conference and Exhibition, 30 September-3 October, New Orleans, Louisiana, 2001.

[17] CHEN G, RUSSELL T. Thermoporoelastic effect on wellbore stability[J]. SPE Journal, 2005, 10: 121-129.

[18] ZHANG J, MAO B, ROEGIERS J C. Dual-porosity poroelastic analyses of wellbore stability[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40: 473-483.

[19] ZHANG J, MAO B, ROEGIERS J C. On drilling directions for optimizing horizontal well stability using a dual-porosity poroelastic approach[J]. Journal of Petroleum Science and Engineering, 2006, 53: 61-76.

[20] ABOUSLEIMAN Y N, CHEN S. Poromechanics response of an inclined borehole subject to in-situ stress and finite length fluid discharge[J]. Journal of Mechanics of Materials and Structures, 2010, 5: 47-66.

[21] CUI L, CHENG A H D, ABOUSLEIMAN Y. Poroelastic solution for an inclined borehole[J]. Journal of Applied Mechanics, 1997, 64:32-38.

[22] ABOUSLEIMAN Y, CUI L. Poroelastic solutions in transversely isotropic media for wellbore and cylinder[J]. International Journal of Solids and Structures, 1998, 35: 4 905-4 929

[23] ABOUSLEIMAN Y, SHAILESH E. Solutions for the inclined borehole in a porothermoelastic transversely isotropic medium[J]. Journal of Applied Mechanics, 2005, 72: 102-114.

[24] 刘喜武. 弹性波场论基础. 青岛: 中国海洋大学出版社, 2008 [LIU X W. Foundation of Elastic Wave Field-theory[M]. Qingdao:Ocean University of China Press, 2008.]

[25] BIOT M A. Propagation of elastic waves in a cylindrical bore containing a fluid[J]. Journal of Applied Physics, 1952, 23: 997-1 005.

[26] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28: 168-178.

[27] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28: 179-191.

[28] SENJUNTICHAI T, RAJAPAKSE R K N D. Transient response of a circular cavity in a poroelastic medium[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17: 357-383.

[29] XIA Y, JIN Y, CHEN M, et al. Poroelastodynamic response of a borehole in a non-hydrostatic stress field[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 93: 82-93.

[30] BRADLEY W B. Failure of inclined boreholes[J]. ASME Journal of Energy Resources Technology, 1979, 101: 232-239

[31] DESAI C S, SIRIWARDANE H J. Constitutive laws for engineering materials, with emphasis on geologic materials[M]. London:Prentice-Hall, 1984.

Poroelastic dynamics mechanisms of wellbore instability in tight formations

TENG Xueqing1,2,3, CHEN Mian1,2, JIN Yan1,2, LU Yunhu1,2, XIA Yang1,2
1 School of Petroleum Engineering, China University of Petroleum-Beijing, Beijing 102249, China 2 State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China 3 PetroChina Tarim Oilfield Company, Kuerle 841000, China

At present, the elastoplastic statistical and poroelastic models are often used to explain the mechanism of wellbore instability. The effect of poroelastic dynamics induced by the wellbore excavation in tight formations in the early times is ignored.In this paper the transient model of wellbore instability in a porous formation with an anisotropic stress field was established.A Fourier transform technique was employed to decompose the governing equation for the 2D heterogeneous stress field into two one-dimensional problems. Meanwhile, the numerical convergence criteria were analyzed, and the effect of poroelastic dimensionless parameters on the transient failure was also included in the modelling process. The results show that: the pore pressure field, effective stress field, tangential stress field and radial stress field near the wellbore calculated by the new model are larger than those calculated by the traditional poroelastic model. Furthermore, shear failure is more likely to occur along the direction of minimum in-situ stress and the failure area increases with time. The fluid saturation in the porous media has the greatest influence on the transient wellbore instability. The wellbore tends be more likely to have higher instability with a higher fluid saturation. The new model established in this paper provides a new method for the wellbore instability mechanism analysis of tight formations and the evaluation of wellbore hydrostatic pressure. Also, it is significant for the management of wellbore stability in tight formations with an extra low permeability.

poroelastic; dynamics; wellbore instability; tight formation

* 通信作者，luyunhu20021768@163.com

2017-05-19

国家自然科学基金面上项目(51774305)、国家自然科学基金重大项目(51490651)和国家杰出青年科学基金项目(51325402)联合资助

滕学清, 陈勉, 金衍, 卢运虎, 夏阳. 致密地层井壁失稳的孔隙弹性动力学机理研究. 石油科学通报, 2017, 04: 478-489

TENG Xueqing, CHEN Mian, JIN Yan, LU Yunhu, XIA Yang. Poroelastic dynamics mechanisms of wellbore instability in tight formations. Petroleum Science Bulletin, 2017, 04: 478-489. doi: 10.3969/j.issn.2096-1693.2017.04.044

10.3969/j.issn.2096-1693.2017.04.044

(编辑 马桂霞)