基于量子遗传算法的电网限流优化措施及应用

谢旗辉

(上海合泽电力工程设计咨询有限公司，上海 200433)

基于量子遗传算法的电网限流优化措施及应用

谢旗辉

(上海合泽电力工程设计咨询有限公司，上海 200433)

短路电流水平过高的站点往往集中在少数的几个区域，可以通过等值减少限流措施配置优化问题的变量数和约束数，在此基础上提出了一种经济有效的综合限流措施配置优化方法。利用Ward等值方法对需要配置限流措施的电网进行等值，减小限流措施配置优化中的计算量，同时为了平衡有效限流和投资的经济性，分析了限流措施的经济成本和限流效果，建立了考虑限流效果和投资成本的限流措施配置优化多目标数学模型。介绍量子遗传算法的原理，提出了基于量子遗传算法求解限流措施配置优化模型的方法。以某地区电网为例，验证了所提方法的正确性和有效性。

短路电流；限流措施；Ward等值；量子遗传算法

随着近几年电网建设的飞速发展，电网物理规模不断扩大。这使得电网各元件间的电气联系加强，短路电流水平日益增大，短路电流已成为电网的热点研究问题之一[1-3]。但在实际电网中，节点的电压方程、功率平衡方程等均涉及全网的变量和约束，但短路电流水平过高的站点往往集中在少数的几个区域，因此可通过等值减少限流措施配置优化问题的变量数和约束数。

本文基于Ward 等值方法，对需要配置限流措施的电网进行等值。在此基础上，为了达到有效而经济的控制电网短路电流水平的目的，分析了限流措施的经济成本和限流效果。综合多种限流措施，建立限流措施配置优化数学模型，寻找限流效果和投资成本最优的综合限流方案[4-7]。介绍量子遗传算法的原理和特点，提出基于量子遗传算法求解限流措施配置优化模型的方法。最后，以某地区电网为例，验证所提方法的正确性。

1 电力网络Ward等值

实际大电网中往往是少数的几个区域存在短路电流水平过高的站点。由于节点电压方程、功率平衡方程等均涉及全网的变量和约束，在优化配置限流措施时若考虑整个电网所有部分，那么其数学模型将会十分复杂，也难以求解。一种可行的办法是将与短路电流水平过高相关性不大的电网部分进行Ward等值[8-9]，留下和短路电流水平相关性大的部分，可以减少模型的变量数和约束数，从而提高短路电流计算和限制措施优化的求解速度。

二区域互联系统等值前后的网络图如图1所示，通过内网边界节点Bi…Bj以及外网边界节点Bm…Bn相连。其中，内网为和短路电流水平过高相关性大的电网部分，也即优化配置限流措施时需考虑的电网部分，外网为和短路电流水平过高相关性不大的电网部分，也即优化配置限流措施时可等值的电网部分。

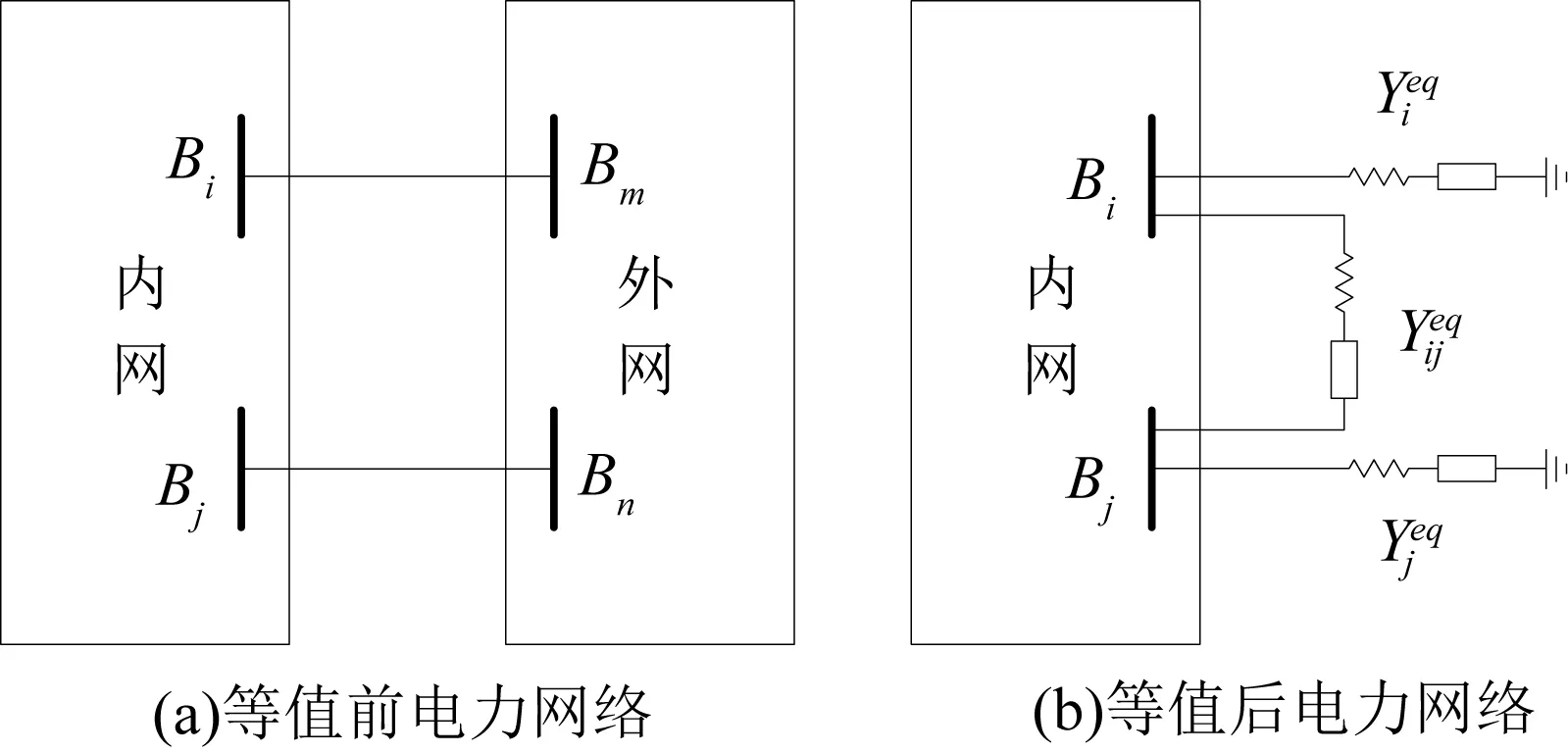
图1 二区域互联电网等值前后的网络图

(1)

(2)

2 限流措施网络分析

假设电网经Ward 等值后保留n个节点，本节将分析等值后电网各限流措施对应的自阻抗变化量计算过程。

2.1 线路开断

如图2所示，节点a和节点b之间相连线路的阻抗为Zab，该线路开断可以用在原运行网络的节点a和节点b之间并联一条阻抗为-Zab的线路来表示，相当于在原网络的节点a和节点b之间追加一条阻抗-Zab为的支路。

图2 线路开断等效示意图

节点a和节点b之间相连线路开断后，短路点节点k自阻抗为：

(3)

2.2 线路出串

线路出串运行可采用追加支路法来处理。如图3所示，初始运行方式下阻抗为Zce的线路ce和阻抗为Zde的线路de在节点e处连接，当线路ce和de出串运行时，相当于先分别开断线路ce和de，然后再在节点c和d之间接入一条阻抗为Zce+Zde的线路。

图3 线路出串运行等效示意图

线路出串运行后短路点节点k自阻抗计算过程为：

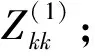
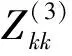
(4)

2.3 加装限流电抗器

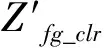
(5)

图4 线路加装限流电抗器的等值图与等效电路图

和线路开断相似，节点f和节点g之间装设限流电抗器也等效于在节点f和节点g之间并联一条支路。因此，节点f和节点g之间装设限流电抗器后，短路点节点k自阻抗为

(6)

2.4 采用高阻抗变压器

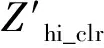
(7)

图5 高阻抗变压器的等值图与等效电路图

和线路开断相似，节点h和节点i之间采用高阻抗电压器也等效于在节点h和节点i之间并联一条支路。因此，节点h和节点i之间采用高阻抗电压器后，短路点节点k自阻抗为

(8)

3 限流措施优化配置模型

为了限制短路电流，假设一共有N条线路可开断、M条线路可出串、H个限流电抗器、G个高阻抗变压器。

3.1 限流措施效果分析

限流措施的最主要目的就是减小电网的短路电流，因此限流措施优化配置模型的目标函数必定要体现短路电流减小效果。本文用施加限流措施前后的短路电流变化作为短路电流减小效果：

(9)

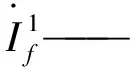
短路电流可根据前一节所提方法求取。因此，对于前述的各种限流措施，其电流减小效果可具体描述为：

(1)对于线路开断，短路电流减小效果为

(10)

式中xl——是否开断线路，开断为1，否则为0。

(2)对于线路出串，短路电流减小效果为

(11)

式中xll——是否实施线路出串运行，实施出串运行为1，否则为0。

(3)对于装设限流电抗器，短路电流减小效果为

(12)

式中xclr——是否装设限流电抗器，装设限流电抗器为1，否则为0。

(4)对于采用高阻抗变压器，短路电流减小效果为

(13)

式中xtra——是否采用高阻抗变压器，采用高阻抗变压器为1，否则为0。

3.2 限流措施经济成本分析

(1)线路开断。若只考虑运行人员的操作成本，线路开断和闭合的成本相同，只跟断路器动作的次数相关，可表示为

C1=xlA1

(14)

式中A1——常数。

若只考虑开关的开合成本，A1为很小值，主要取决于人工费和断路器的损耗成本等，但往往线路的开合需要考虑更多因素，比如经济运行、稳定运行等问题。当线路的开断不影响系统稳定性和可靠性时，本文简单的认为它是一种最经济最简单的限流措施，此时，它的成本可以取较小值。

(2)线路出串。线路出串问题中涉及的线路倒闸操作，本质是线路的开断与闭合。因此，和线路开断类似，其成本可表示为

C2=xuA2

(15)

式中A2——常数。

(3)限流电抗器。限流电抗器的造价和安装等费用跟其阻值大小有关，阻值越大，相关费用就越高。加装的投资成本可以计算为

C3=xclr(A3+B3Zclr)

(16)

式中A3和B3——成本系数，与接入的电压等级相关。

(4)采用高阻抗变压器。内置电抗器型高阻抗变压器的投资成本与内置电抗器的阻抗大小有关，阻值越大，投资成本越高

C4=xtra(A4+B4Ztra)

(17)

式中A4和B4——成本系数，与接入的电压等级相关。

3.3 限流措施配置多目标优化模型

根据上面各限流措施的限流效果和成本分析，建立限流措施配置多目标优化模型如下。

目标函数

(18)

约束条件

(19)

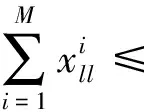
(20)

(21)

(22)

4 基于量子遗传算法求解

量子遗传算法(QGA)是基于传统的遗传算法而改进得到的一种基于量子计算原理的概率优化方法。

4.1 初始种群

xj(w)表示为w代第j个染色体。种群中全部染色体的所有基因概率幅 (αij,βij) 的初值，全部为 (1/sqrt(2),1/sqrt(2))，其平方和为1。

4.2 个体测量

测量过程为：随机产生一个0～1之间的数，若它大于概率幅的平方，则测量结果取值为1，否则取值为0。

4.3 个体评价

用适应函数对R(w)中的每个个体进行评价，若获得了满意的解或达到结束条件，中止迭代；否则转下一步。

4.4 种群更新

使用恰当的量子门U(w)，即旋转门更新X(w)，更新种群。

基于量子遗传算法的限流措施配置优化流程如图 6所示。

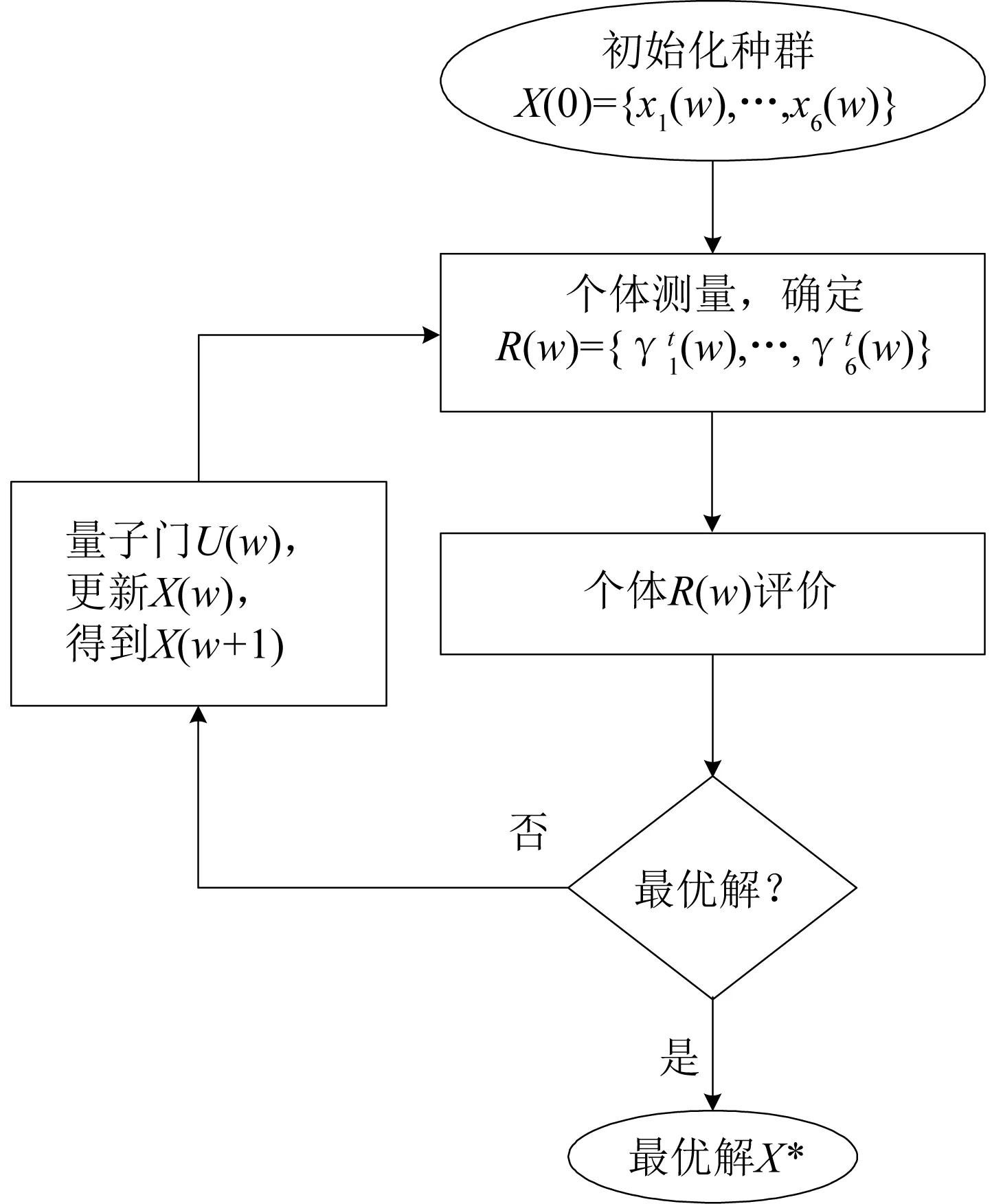
图6 基于量子遗传算法的限流措施优化流程图

5 算例

对该地区电网进行Ward 等值，简化后共19个节点，如图7所示，其中750 kV节点3个，330 kV8个，220 kV节点8个。由于750 kV联网和大机组群(G1、G4等)的接入，使得系统短路电流显著提高，而节点GA220的短路电流达到了51.3 kA，超过了所安装断路器(额定遮断电流为50 kA)的遮断能力，其他节点的短路电流都不高于断路器的遮断电流。

限流措施考虑线路开断、出串运行、加装限流电抗器和采用高阻抗变压器。开断线路备选集为：7；出串运行备选集为：线路1和8、线路2和9；可安装限流电抗器的线路备选集为：1、2、7、8、9；可采用高阻抗电压器的备选集为：GA变电站内变压器。各限流措施对应的成本系数在表1中给出。

图7 Ward等值后系统图

表1 限流措施成本系数

根据本文提出方法，综合考虑投资费用最小化和短路电流降低，以短路电流、优化变量不越限为约束条件优化限流措施。量子遗传算法设置种群数目为100，目标函数权重系数和取为0.01和0.99，进行10次重复仿真，每次最优方案均为线路1和8出串运行，且量子遗传算法收敛次数在45到60之间。

为了说明投资费用和系统最大短路电流之间的关系，以10次仿真中某一次为例，图8给出了迭代过程中投资费用和系统最大短路电流之间的关系曲线。从图8中可以看出，投资费用和系统最大短路电流呈反比例关系，即投资成本越少则限流效果越差，投资成本越多则限流效果越好。在实际选用限流措施时，应综合考虑限流实际需求和经济性。

图8 限流措施成本与短路电流关系曲线

如果电网不经过Ward等值而直接进行限流措施配置优化，其各限流措施备选集空间将大大增加。同样利用则量子遗传算法求解，设置种群数目为500，经过50次重复仿真，结果统计如表2所示。从表中可以看出，未经Ward等值，由于电网物理规模较大，潜在限流措施较多，算法易陷入局部收敛。

表2 电网不经过Ward等值时限流措施配置优化50次仿真结果统计

6 结语

本文提出了基于量子遗传算法的限流措施配置优化方法。通过对需要配置限流措施的电网进行等值，减小了限流措施配置优化中的计算量。为了平衡有效限流和投资的经济性，给出了限流措施的经济成本和限流效果数学表达式，建立了限流措施多目标配置优化数学模型。提出了基于量子遗传算法求解限流措施配置优化模型的方法，大大提高了搜索限流措施配置优化最优解效率。最后，以某地区电网为例，验证了所提方法的正确性。

[1] 龚贤夫，高崇，龙志，等. 500 kV 自耦变压器中性点加装小电抗限制不对称短路电流原理[J]. 电力建设, 2013, 34(11): 56-60.

GONG Xianfu, GAO Cong, LONG Zhi, et al. Principle of limiting asymmetric short-circuit current by installing small reactance at 500 kV autotransformer neutral point[J]．Electric Power Construction，2013，(11)：56-60．

[2]罗涛，刘丽霞，王魁，等. 特高压接入对天津500 kV 电网短路电流影响及限制措施[]J]. 电力建设, 2015, 36(8):79-83.

LUO Tao, LIU Lixia, WANG Kui, et al. Influence of UHV grid on short-circuit current of Tianjin 500 kV Grid and its restrictive measures[J]．Electric Power Construction，201 5，36(8)：79-83．

[3]孙毅卫，王志文，汪雨辰，等. 含高密度分布式电源的配电网短路电流快速计算方法[J]. 电力建设, 2016, 37(5):118-124.

SUN Yiwei, WANG Zhiwen, WANG Yuchen, et al. A fast calculation method for short circuit current of distribution network with numerous distributed resources[J]．Electric Power Construction，2016，37(5)：118 -124．

[4]唐君华，涂春鸣，姜飞，等.限流式动态电压恢复器及其参数设计[J].电力系统保护与控制,2015,43(24):115-121.

TANG Junhua, TU Chunming, JIANG Fei, et al. Dynamic voltage restorer with current limiting function and its parameter design[J]. Power System Protection and Control，2015，43( 24)：115-121．

[5]杨杉，同向前，王海燕，等.换流器限流状态下的配电网潮流计算方法[J].电力系统保护与控制,2017,45(3):1-6.

YANG Shan, TONG Xiangqian, WANG Haiyan, et al. Power flow calculation for distribution network under the current limiting status of grid-connected inverter[J].Relay,2017,45(3):1-6.

[6]杨雄平，李力，李扬絮，等. 限制广东500 kV电网短路电流运行方案[J]. 电力系统自动化, 2009, 33(7): 104-107.

YANG Xiongping, LI Li, LI Yangxu, et al. Research on short-circuit current exceeding limit of 500kV power network in Guangdong in 2009[J]. Automation of Electric Power Systems，2009，33(7)：104-107．

[7]陈丽莉，黄民翔，张弘，等. 电网限流措施的优化配置[J]. 电力系统自动化, 2009, 33(11):38-42.

CHEN Lili, HUANG Minxiang, ZHANG Hong, et al. An optimization strategy for limiting short circuit current[J]. Automation of Electric Power Systems，2009，33 (11)：38-42．

[8]邵玉槐，李肖伟，程晋生. REI 等值法用于多节点配电系统短路电流计算的研究, 中国电机工程学报[J]. 2000,20(4):64-67.

SHAO Yuhuai, LI Xiaowei, CHENG Jinsheng. Studies on applying rei method to computing short-circuit fault current of distribution system of many nodes[J].Proceedings of the CSEE,2000,20(4):64-67,88.

[9]孙奇珍，蔡泽祥，朱林，等. 互联电网的多端等值方法及其误差分析, 电网技术[J]. 2008, 32(23): 67-71.

SUN Qizhen, CAI Zexiang, ZHU Lin, et al. Multi-terminal equivalence method of interconnected power system and improvement based on its error analysis [J]. Power System Technology, 2008，32(23)：67-71．

CurrentLimitingOptimationMeasureofPowerGridBasedonQuantumGeneticAlgorithmandItsApplication

XIE Qihui

(Shanghai Heze Electric Power Engineering Design Consulting Co., Ltd., Shanghai 200433, China)

The locations of excessively high short-circuit current level are often concentrated in a few areas, and the number of problematic variables and constraints can be configured and optimized by the current limiting measures of the equivalent reduction. Thereupon, an economical and effective comprehensive current limiting measure is proposed. Configure the equivalent by means of Ward equivalent method for power grid current limiting, reduce the amount of calculation in current limiting measure configuration and optimization; meanwhile analyze the economic cost and current limiting effect of current limiting measures in order to balance between the current limiting effect and the investment economy; establish the multi-objective mathematical model considering current limiting effect and the investment cost. It also introduces the principle of quantum genetic algorithm (QGA) and proposes a QGA-based method to solve the current limiting measure optimation model. The correctness and validity of the proposed method are verified by the example of the power grid in a certain region.

short circuit current; current limiting measures; Ward equivalent; quantum genetic algorithm (QGA)

10.11973/dlyny201705015

谢旗辉(1983—)，男，硕士，从事配电网研究分析工作。

TP18；TM73

A

2095-1256(2017)05-0554-06

2017-06-18

(本文编辑：赵艳粉)