离心率求解策略例谈

河北 朱建国

离心率求解策略例谈

河北 朱建国

圆锥曲线作为比较重要的一种曲线类型，由于其特殊的形式和性质而频繁出现在高考试题中.而离心率是描述圆锥曲线形状特征的一个重要概念，是三类二次曲线(椭圆、双曲线、抛物线)统一定义的桥梁和纽带.离心率问题内涵丰富且综合性强，历年来是高考中的考查重点和热点.

对于求圆锥曲线离心率的问题，通常有两类：一是求椭圆和双曲线的离心率；二是求椭圆和双曲线离心率的取值范围.本文结合实例，分析求解离心率的常用策略.

一、借助定义(或第二定义)求离心率

【解析】由双曲线的定义可知||PF2|-|PF1||=2a,

又|PF1|=4|PF2|，所以|PF1|-|PF2|=2a.

【评注】点P在椭圆或双曲线上，左、右焦点分别为F1，F2，椭圆的定义|PF2|+|PF1|=2a；双曲线的定义||PF2|-|PF1||=2a.

( )

A.(1,2) B.(2,+∞)

C.(1,5) D.(5,+∞)

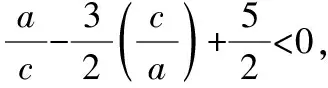
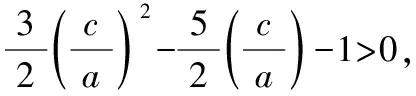
所以3e2-5e-2gt;0，即(3e+1)(e-2)gt;0.

又egt;1,所以egt;2.故选B.

【评注】由圆锥曲线的第二定义可知，圆锥曲线的离心率e是平面上动点到焦点的距离和该动点到对应准线的距离之比，特别适用于条件中含有焦半径的问题.

由圆锥曲线的统一定义知，

由|PF1|是P点到准线l的距离d与|PF2|的等比中项知|PF1|2=d×|PF2|，

由于P是双曲线左支上一点，故有x0≤-a，

整理得a2=3c2，

二、利用方程思想求离心率

( )

【评注】根据题设条件，借助a，b，c之间的关系，列出关于a，c的方程关系式，进而得到关于离心率e的方程，从而通过解方程来得到离心率e，关键是构造相应的方程，但解方程时要注意对应圆锥曲线的离心率的特征.

( )

三、数形结合求离心率

【解析】如图，设OF的中点为T，

【评注】离心率具有明确的几何意义，在某些问题中，借助数形结合，由“数”到“形”加以转化，画出合适图形，找出a，b间的关系，则双曲线的离心率的求解过程会相对便捷很多，能够大大提高解题速度和正确率.

【变式4】已知A，B为双曲线E的左、右顶点，点M在E上，△ABM为等腰三角形，且顶角为120°，则E的离心率为

( )

四、利用焦点三角形求离心率

【解析】 根据正弦定理，

因为egt;1，所以PF1gt;PF2，点P在双曲线的右支上．

又PF1-PF2=ePF2-PF2=PF2(e-1)=2a，

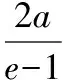
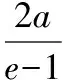
椭圆的焦点三角形是指以椭圆的两个焦点F1，F2与椭圆上任意一点P为顶点组成的三角形，灵活运用其定义和性质也可求解离心率.

( )

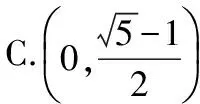
【简解】本题可以用焦点三角形求解,

由对称性AF2=BF2，只要∠AF2Blt;90°⟹∠AF2F1lt;45°即可满足△ABF2为锐角三角形，

五、利用函数思想求离心率

( )

【解析】根据双曲线离心率公式，显然

【评注】当所求离心率转化为某参数的二次函数(或类二次函数)时，可以利用二次函数的性质确定离心率的范围；如果能够构造出现夹角，就可以将离心率转化为角的函数，再利用三角函数求最值，进而求得离心率.

( )

A．(1,3) B．(1,3]

C．(3,+∞) D．[3,+∞)

六、利用向量求离心率

( )

【简解】设双曲线的右焦点为F1，连接PF1，

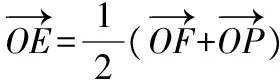
又O是FF1的中点，所以OE∥PF1，

由|PF|2+|PF1|2=|FF1|2，|PF1|=a，

|PF|=2a+|PF1|=3a，所以9a2+a2=(2c)2，

由上可见，离心率的求解方法多种多样，我们在处理有关离心率的问题时，必须注意分析判断问题的类型，以选择合适的方法进行求解.

七、结合直线与圆锥曲线的位置关系求离心率

【解析】设点A(x1，y1)，点B(x2，y2)，点M是线段AB的中点，

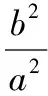
【评注】如果题中给出直线与圆锥曲线的位置关系，可以根据相关的条件建立含a,b,c的方程，也可以进一步求得离心率.

( )

河北省衡水市第一中学)