解三角形的几个技巧

山西 李有贵

解三角形的几个技巧

山西 李有贵

解三角形问题的常规解法是利用正余弦定理，以及三角函数公式求解.孰不知勾股定理是余弦定理的特殊情形，锐角三角函数的定义方法是在直角三角形中定义的，因而解三角形的问题，可以通过作高得到直角三角形，利用三角函数的定义、勾股定理,以及特殊直角三角形来解题.

一、构造特殊直角三角形解题

【解析】如图，作AE⊥BC于E,CF⊥AB于F.

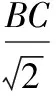
由勾股定理得

所以∠BAC=60°.

二、利用三角函数的定义解题

【例2】已知在△ABC中，若C=120°,tanA=3tanB，sinA=msinB,则实数m=________.

【解析】如图，

作AD⊥BC交BC延长线于D，设CD=1，

【评注】过A作三角形的高AD.由C=120°为特殊角，既可以利用特殊直角三角形中三边之间的关系，又可以利用三角函数的定义得到tanA,tanB的表达式，因而可以利用方程求解.利用两角和的正切公式求出x后，利用正弦定理求出m.

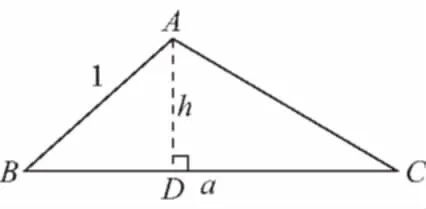
【简解】如图，作AD⊥BC于D，

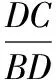
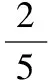
在△ABD中，

三、转化为方程(组)解题

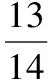
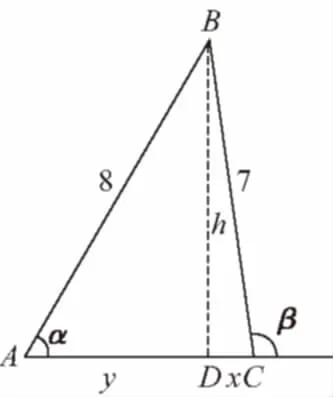
在△BCD，△ABD中，由勾股定理得

x2+h2=49②,y2+h2=64③,

③-②得y2-x2=15,即(y+x)(y-x)=15,

②+③-2×①得(y-x)2=9，即y-x=3.

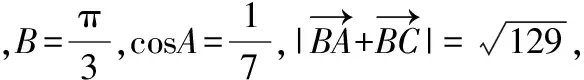
【简解】如图，作平行四边形BADC，

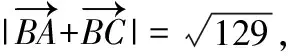
作CE⊥AB，DF⊥AB，垂足为E,F.

所以△BCE≌△ADF.

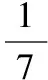
所以AF=BE=4x.在△BDF中，

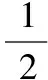
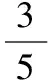
四、构造相似三角形解题

【例4】已知△ABC，AB=AC=4,BC=2，点D为AB延长线上一点，BD=2，连接CD，则△BDC的面积是________，cos∠BDC=________．

【评注】求三角形面积最常用的公式是底与高的积的一半，求角的余弦值用三角函数定义求解.因而想到作AB边上的高CE，BC边上的高AF，利用等腰三角形性质，构造相似三角形求解.

山西省临县第一中学)