抛开线性规划，不等式运算搞定

江苏 王安寓

抛开线性规划，不等式运算搞定

江苏 王安寓

有一些函数题目，往往易于联想到运用线性规划知识方法求解，殊不知，有些题目不是考查线性规划的，而是考查不等式运算的．如果运用线性规划求解，那么，费时费力不说，还有可能求解不出，或因运算过程复杂而致错．以线性规划的样子呈现，并不意味着让你运用线性规划知识求解．首先，条件简单翻译后是不等式组(或者条件直接就是不等式组)，不等式组本身就是不等式，何不用不等式运算求解？其次，不等式运算包括：①不等式的定义；②不等式的性质；③基本不等式或柯西不等式等公式．

一、巧妙换元，分离参数，不等运算，各个击破

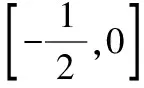
分析：我们注意到a，b与x是两组自由的量，因此我们可以分开处理．通过换元，将这种关系显化．

∴a-2b=t∈[0，1]．

评注：本题极易想到用线性规划求解，这样做势必会造成运算量的大大增加(要讨论要转化为不等式组要画图要识图)．该解析采用的是各个击破的策略．先解决s，再解决u．解题既有层次性，又不互相干扰．这是计算策略的选择对解题过程的影响．这样就达到了小题少算，小题巧做的目的．但是这需要平时解题时进行解题后的反思，提高认识，从中感悟．这样才能在应试中巧法妙算应运而生，信手拈来．

二、变换主元，比例相等，构建方程，回代求解

【题目2】(2017·南通二模·14)已知对任意的x∈R，3a(sinx+cosx)+2bsin2x≤3(a,b∈R)恒成立，则当a+b取得最小值时，a的值为________．

分析一：将目标与条件结合，可视条件为a，b的不等式，而目标也是关于a，b的不等式，可以认为条件与目标之间存在倍数关系，由此引入比例得方程，得解t，再回代求得a+b的最值及取得最值时a，b的值．

解析一：

条件化为3at+2b(t2-1)≤3，①

令a+b=-2，得b=-a-2，

代入①式得2(-a-2)t2+3at+(2a+1)≤0，

∵方程2(-a-2)t2+3at+(2a+1)=0有一根

∴(2t+1)[(-a-2)t+(2a+1)]≤0恒成立，

评注：解析一是小题巧做，是目标意识的具体体现．解题要先明确解题目标，再寻求实现解题目标的方向和合适的解题步骤的过程．解题的关键步骤是：(1)视a，b为主元；(2)条件与目标整合，由系数成比例构造方程．解析一脱离x，研究a，b，得到的是直线或二元不等式．

分析二：方法一由a+b的最小值求a时回代，验证恒成立，计算稍显繁琐．实际上，二次函数最小值的取得往往在对称轴处，因此，可简化计算．

条件化为3at+2b(t2-1)≤3，

评注：解析二是解析一的改进，区别在于a+b取最小值时，a，b的值的求法不同．解析一是通过回代、不等式与方程的关系、完全平方的非负性；解析二是对称轴、最小值构建方程组．解析一是逐步消元(蚕食)，解析二是联立方程组(吞枣)．

【变式1】设函数f(x)=2ax2+bx-3a+1．当x∈[-4，4]时，f(x)≥0恒成立，则5a+b的最小值是________．

【变式2】(2009·北约自主招生)已知对x∈R，acosx+bcos2x≥-1恒成立，求a+b的最大值．

三、适当分离，函数位置，比例截距，识图运算

通过上述解析，我们看到：目标的合理确定对运算的途径设计有很大的影响，一个合理的运算不仅要求运算正确，而且要求运算过程中的每一步都有依据，要合乎算理．

四、导数转移，不等运算，基本公式，和积互化

( )

A.16 B.18

分析：函数单调性往往转化为导数的符号判定，进而转化为不等式组，但不要用线性规划，目标是求乘积的最大值，这与基本不等式有关，因此要考虑条件中的和，进而运用基本不等式求解．

∴f′(x)≤0，

∵m≥0，n≥0，∴0≤m≤6．

当2lt;m≤6时，由②得2m+n≤12，

当且仅当m=3，n=6时取等号．

当0≤mlt;2时，由①得m+2n-18≤0，

综上mn的最大值为18，当且仅当m=3，n=6时取得最大值．

评注：待求目标的几何意义不明显，但是其形式显然——两个正数的积，应与两个正数的和相关．因此，该解法才是最本质的求解方法，而不用线性规划．

五、形式线性，实质不等，不等运算，轻松最值

解析：∵x-y-1lt;0，∴xlt;y+1．

此时不可能达到最大值；

∵4x-y-3≥0，∴4x-y-1≥2．

评注：这种方法涉及的都是基础知识(基本的不等式运算和两个正数的均值公式)，一点也不超纲．看到不等式组的条件，就一定用线性规划吗？思维不能僵化．要用慧眼识别雾中花，基础知识搞定它．

江苏省南京市六合区实验高级中学)