商榷2017年高考题中表述欠严谨的几道题
2017-12-14北京甘志国
北京 甘志国
商榷2017年高考题中表述欠严谨的几道题
北京 甘志国
一年一度的高考是考生、老师、家长、学校乃至全社会关注的重点话题.2017年的高考已尘埃落定,笔者作为一名高中数学老师,也抓紧时间认真钻研了本年度的高考数学真题(文理共计15套,其中上海、浙江文理同卷,江苏文理除附加题外同卷),发现了它们有试题常规、情景新颖、杜绝偏怪、难度在较大幅度的降低、文理相同题或姊妹题在增多等特点,这也与新课改的精神、教育乃培养人的活动、数学本来应当是人人能够喜爱的美的科学合拍.
但笔者发现有少量高考题在表述上欠严谨:虽然原题不会太影响考生正确答题,但作为高考题的权威性及引用的广泛性,还是要注意表述上的严谨.
笔者分别对2016、2015、2014年的高考题在表述上欠严谨之处也作了商榷.

(Ⅰ)求f(x)的导函数;

题2(2017·江苏卷·20)已知函数f(x)=x3+ax2+bx+1(agt;0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(Ⅰ)求b关于a的函数关系式,并写出定义域;
(Ⅱ)证明:b2gt;3a;

商榷普通高中课程标准实验教科书《数学·选修2-2·A版》(人民教育出版社,2007年第2版)第9页写到:“当x变化时,f′(x)便是x的一个函数,我们称它为f(x)的导函数(derivative function)(简称导数)”.既然教科书中已写到“导函数简称导数”,数学表述应以简洁为标准,所以建议把题1中的“(Ⅰ)求f(x)的导函数”改为“(Ⅰ)求f(x)的导数”或“(Ⅰ)求f′(x)”;建议把题2中的“导函数f′(x)”改为“导数f′(x)”或“f′(x)”.
题3(1)(2017·天津卷文·2)设x∈R,则“2-x≥0”是“|x-1|≤1”的
( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件

( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
(3)(2017·浙江卷·6)已知等差数列{an}的公差为d,前n项和为Sn,则“dgt;0”是“S4+S6gt;2S5”的
( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
(4)(2017·北京卷·理6,文7)设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·nlt;0”的
( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
商榷普通高中课程标准实验教科书《数学·选修2-1·A版》(人民教育出版社,2007年第2版)(下简称《选修2-1》)第11页写到:“……此时,我们说,p是q的充分必要条件,简称充要条件(sufficient and necessary condition)”.既然教科书中已写到“充分必要条件简称充要条件”,数学表述应以简洁为标准,所以建议把本题第(3),(4)小题选项C中的“充分必要条件”均改为“充要条件”.建议把《选修2-1》第30页第2(3)题末的“充分必要条件”也改为“充要条件”.
与《选修2-1》配套使用的《教师教学用书》(人民教育出版社,2007年第2版)第11页给出的《选修2-1》第12页第3题的答案是“(1)充分条件,或充分不必要条件;(2)充要条件;(3)既不是充分条件,也不是必要条件;(4)充分条件,或充分不必要条件.”所以建议把本题第(1),(2),(4)小题选项A,B中的“而”字均去掉.
题4(2017·山东卷理·18)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的频率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
商榷建议把题末的“EX”改为“E(X)”,这样才与现行教材一致.
题5(2017·全国卷Ⅱ理·13)一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则DX=________.
解由题可得X~B(100,0.02),所以DX=100×0.02×0.98=1.96.
商榷建议把题中的“DX”改为“D(X)”,这样才与现行教材一致.
题6(2017·上海卷·15)已知a,b,c为实常数,数列{xn}的通项xn=an2+bn+c,n∈N*,则“存在k∈N*,使得x100+k,x200+k,x300+k成等差数列”的一个必要条件是
( )
A.a≥0 B.b≤0
C.c=0 D.a-2b+c=0
商榷建议把题中的“通项”改为“通项公式”,这样才与现行教材一致.
普通高中课程标准实验教科书《数学5·必修·A版》(人民教育出版社,2007年第3版)第29页写到“如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.”

题7(2017·全国卷Ⅰ文·17)记Sn为等比数列{an}的前n项和.已知S2=2,S3=-6.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列.
商榷题末的句号应改为问号.
题8(2017·全国卷Ⅰ理·19)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(Ⅰ)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(Ⅱ)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:

9.9510.129.969.9610.019.929.9810.0410.269.9110.1310.029.2210.0410.059.95

附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σlt;Zlt;μ+3σ)=0.997 4.

商榷普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社2009年第3版,2015年第2次印刷)第73页给出的数据是
P(μ-σ≤X≤μ+σ)=0.682 6
P(μ-2σ≤X≤μ+2σ)=0.954 4
P(μ-3σ≤X≤μ+3σ)=0.997 4
而该书“2016年第3次印刷”时给出的数据是
P(μ-σ≤X≤μ+σ)=0.682 7
P(μ-2σ≤X≤μ+2σ)=0.954 5
P(μ-3σ≤X≤μ+3σ)=0.997 3
这次高考题中给出的数据又是“P(μ-3σ≤X≤μ+3σ)=0.997 4”.建议给出权威、统一的数据.
题9(2017·北京卷文·15)已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求和:b1+b3+b5+…+b2n-1.
解(Ⅰ)(过程略)an=2n-1.
(Ⅱ)设等比数列{bn}的公比为q,由题设可得
b2b4=b1q·b1q3=(q2)2=9,q2=±3.
①当q2=3时,b2n-1=b1(q2)n-1=3n-1,

②当q2=-3时,b2n-1=b1(q2)n-1=(-3)n-1,

评注该解法(在复数范围内求解)显然不是出题者的初衷,但是目前的文科、理科高三学生都学习了复数,所以以上解法并无不妥.

解答题10时也会遇到这样题9的情形.所以建议把题9及题10中的“等比数列”都改成“各项都是实数的等比数列”.



证明设P(x,y)(x≤-a),
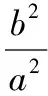
由x≤-a,可得|PF|的取值范围是[c-a,+∞).
同理可证,|QF|的取值范围是[c+a,+∞).


( )
A.1033B.1053C.1073D.1093

北京市丰台二中)
