基于压缩感知的图像重构关键技术研究

刘效勇，卢佩*，曹海宾，田敏

（1石河子大学理学院，新疆 石河子832003；2石河子大学信息科学与技术学院，新疆 石河子832003）

基于压缩感知的图像重构关键技术研究

刘效勇1，卢佩2*，曹海宾1，田敏2

（1石河子大学理学院，新疆 石河子832003；2石河子大学信息科学与技术学院，新疆 石河子832003）

图像在信息领域应用的重要性使人们对快速成像技术提出了更高需求，压缩感知理论为图像处理提供了一种新途径。本文研究了压缩感知理论应用于图像重构的关键技术，重点分析对比了各种因素对重构图像质量的影响。实验结果表明：通过小波变换基对信号稀疏，以哈达玛矩阵作为测量矩阵，使用正交匹配追踪算法时仅需50%的采样率即可获得较高质量的图像，有效减少了传统方法中冗余数据过多问题，在重构图像视觉效果和PSNR值上均有所提高，同时提高了恢复效率。本研究为应用压缩感知寻求最优化图像恢复方法在理论和技术上提供了有力依据和支撑。关键词：压缩感知；图像重构；稀疏信号；测量矩阵；重构算法

现实世界的虚拟仿真以及对处理信号数字化，决定了从模拟信号源获取数字信息时必须通过信号采样。但是在数字图像以及语音视频的获取过程中，按照传统的奈奎斯特采样定理进行采样容易导致采样数据过多；另外，随着人们对信息需求数量的不断增长，要求信息载体的带宽愈来愈宽，采集速率以及信号处理速度也会愈来愈高，这给信号的采集、处理、传输以及存储等带来了很大的挑战。

学者们[1-3]提出了一种新颖的信息获取理论，即压缩感知（compressed sensing，CS）[1-3]，该理论指出：当信号具有稀疏性或可压缩性时，采集少量数据就可精确或近似精确地重构原始信号。压缩感知突破了传统的信号采样瓶颈，能够以远低于奈奎斯特采样频率采样和恢复信号，因而可以更加有效存储和传输信息。该理论一经提出就受到国内外科研人员的高度关注。目前，压缩感知技术已被广泛应用在计算机图形学、天文学、医学成像、高光谱成像、远距离遥感、模拟-信息转换、地球物理学数据分析、生物传感、分布式压缩感知等领域中[4-6]。此外，多种压缩感知硬件相继出现，如美国麻省理工大学L.Wald等人研制的MRJ RF脉冲设备，W.Freeman等人研制的编码孔径相机、美国莱斯大学研制的单像素照相机、美国伊利诺伊州立大学Milenkovic等人研制的DNA微阵列传感器、美国耶鲁大学研制的超光谱成像仪、中科院李廉林等人研制的CS滤波器和混沌腔等[7-11]。这些压缩感知硬件仪器的实现使压缩感知理论向实用化前进了一大步。

应用压缩感知，可以有效地提高应用系统的性能、缩短数据获取的时间、降低数据获取的耗能、减少数据的存储空间、提高数据的传输速度等。压缩感知与信号的稀疏重构尤其是在图像的压缩与重建方面有着非常大的应用价值。然而，由于缺乏有效的压缩传感矩阵判别理论，重构算法需要迭代运算，造成复杂度高速度慢，算法过程不可控，参数敏感等问题。另外，实际应用时也容易出现压缩比太大，恢复出的图像效果严重模糊，无法使用。为此，本文从多个方面对影响压缩感知信号重构的因素做了初步探索研究，以便从中找到压缩感知重构图像的最优化方法，从而提高重构信号的效率和质量。

1 压缩感知基本理论框架

压缩传感理论主要包括信号的稀疏表示、编码测量和重构算法等三方面[12-15]。

考虑长度为N的一维实值离散时间信号x，可看作RN空间N×1维的列向量，元素为x[n]，n=1，2，...，如果是图像或高维数据矢量，则转化成一个长的一维向量。RN空间的任何信号都能用N×1维的正交基的线性组合表示。把向量"作为列向量形成N×N的基矩阵ψ=ψ1,ψ2,…ψN，则任意信号x都可以表示为：

其中α为N×1列向量的加权系数，T表示转置操作，x和α是同一个信号的等价表示，x是信号在时域的表示，α则是信号在ψ域的表示。如果式（1）中α只有 K（KN）个非零（或绝对值较大）的系数，x称为K稀疏信号。信号的可稀疏性表示是压缩感知的先验条件，在已知信号是可压缩的前提下，压缩感知过程可分为两步：

（1）设计1个与变换基不相关的M×N（M N）维测量矩阵对信号进行观测，得到M维的测量向量。

（2）由M维的测量向量重构信号。

用1个与变换矩阵不相关的测量矩阵φ对信号进行线性投影，得到线性测量值y：

其中φ是个M×N的随机测量矩阵，=φψ。构造合理有效的测量矩阵是压缩感知研究的核心问题。Candès等[2]指出，高斯随机变量形成测量矩阵可以作为普适的CS观测矩阵。

因为y的维数小于x的维数，所以公式(2)有无穷解，重构原始信号比较困难。既然x为K稀疏，可以利用下面的优化问题求解x：

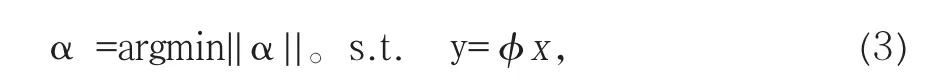
当M≥cKlog(N)时，φ具有有限等距性(RIP)，x[n]能被重构，此处c是个小常系数。

上面的问题可以通过贪婪迭代算法解决，其中最常用的是使用正交匹配追踪算法(OMP)。

最后，当稀疏系数α被精确重构后，通过ψ的逆矩阵重构信号x：

压缩感知指出：当信号在某个变换域是稀疏的或可压缩的，可以利用与变换矩阵非相干的测量矩阵将变换系数线性投影为低维观测向量，同时这种投影保持了重建信号所需的信息，通过进一步求解稀疏最优化问题就能够从低维观测向量精确地或高概率精确地重建原始高维信号。在该理论框架下，采样速率不再取决于信号的带宽，而在很大程度上取决于2个基本准则：稀疏性和非相干性，或者稀疏性和等距约束性。

2 影响压缩感知重构信号质量的关键技术研究

压缩感知能够依据少量采样数据，从低维观测向量精确地重建原始高维信号。该理论包含3个关键部分：稀疏变换基、测量矩阵和重构算法。因此，通过压缩感知理论对原始信号进行采样与重构，在重构过程中信号自身的稀疏程度，信号采样率、选用的测量矩阵和重构算法等不可避免地影响重构信号的质量，为此，本研究从以上几个重要方面对影响信号压缩感知信号重构的因素做了初步探索研究。为了更能直观地判断各算法的恢复效果，以重构图像和原始图像的峰值信噪比(PSNR)、信噪比(SNR)、均方差（MSE）值以及运算速度(Run-Time，RT)作为评判重构图像效果的客观评价标准。

2.1 采样率对重构信号质量的影响

实验中选用256*256像素的经典灰度图像“lena”进行测试，测量矩阵使用高斯随机矩阵构造，重构图像时采用正交匹配追踪算法。图1为采样率(Sampling Rate，SR)分别为20%至80%时图像的重构效果图。由实验结果可见，在测量矩阵和恢复算法相同的情况下，信号的采样率越高重构图像的质量越好。采样率大于50% 时恢复结果比较清晰；采样率为40% 时，仍能较好的重构图像；在采样率为30% 时，恢复的效果很差，出现了较多噪声，图像大部分细节信息丢失。这也验证了压缩感知的测量值与信号稀疏度的关系，只有当测量值大于某个固定范围时，即满足测量值M≥cKlog(N)时，才能较好的构建出原始图像。当然，随着采样率的增大，采样的测量值就越多，运算所需时间就越长。

图1 采样率不同时图像重构效果对比Fig.1 Results contrast under different sampling rate

2.2 稀疏变换基对重构信号质量的影响

应用压缩感知理论对信号处理性能分析，必须保证该信号在某个特定正交空间上是稀疏的。由于1个信号的稀疏性与所选取的正交空间特性密切相关，因而，选用1个最合适的稀疏变换域将其表示出来非常重要。为此，此处对同一个信号数据矩阵稀疏变换基分别采用离散余弦变换 (DCT)，快速傅里叶变换(FFT)和小波变换(DWT)[16-18]，对比重构信号的质量和性能。在重构过程中，测量矩阵使用高斯矩阵，重构算法使用正交匹配追踪算法。

实验中的测试图像仍然选用256*256像素的“lena”灰度图像，原始图像的采样率(M/N)分别为40%、50%、60%时，各种情况下重构质量如表1所示。比较分析结果（表1）可见，相同的采样率下，采用小波变换时重构图像质量最好，并且运行时间最快。采用离散余弦变换时恢复图像质量效果最差，而采用快速傅里叶变换所需时间最长。因而，对信号进行稀疏时应以使用小波变换为宜。

表1 稀疏变换基不同时图像重构效果对比Tab.1 Results contrast under different sparse transform basis

接表1

2.3 测量矩阵对重构信号质量的影响

测量矩阵是压缩感知中最重要的部分，在原始信号抽样的获取与信号重建过程中起着关键性作用。因此，测量矩阵的选择和构造是压缩感知的核心内容，在测量矩阵设计时应首先考虑到2个基本准则：具有有限等距性、测量矩阵和稀疏矩阵间具有不相关性。

测量矩阵之间性能各有差异，实际使用时尽量选用性能尽可能好的测量矩阵。此处选择了目前经常使用的已被发现且具有较好性质的高斯矩阵(Gauss Matrix)、哈达玛矩阵 (Hadamard Matrix)、伯努利矩阵 (BernouliMatrix)、部分正交矩阵(Partial OrthogonalMatrix)以及诺斯莱特矩阵(Noiselets Matrix)作为测量矩阵时重构信号的效果[19-21]，实验中使用256*256像素的灰度图像“flower”做为测试图像，通过小波变换基对信号稀疏，正交匹配追踪(OMP)算法进行信号重构。由实验结果（图2）可见，相同采样率下，使用高斯矩阵、哈达玛矩阵和部分正交矩阵作为测量矩阵时重构图像运行时间较短，而将伯努利矩阵和诺斯莱特矩阵用作测量矩阵时恢复图像耗时较长；使用诺斯莱特矩阵作为测量矩阵图像重构效果最为理想，使用哈达玛矩阵和部分正交矩阵时恢复重构效果差别不是很大，采样率较低时，使用伯努利矩阵重构效果最不理想。

图2 测量矩阵不同时图像重构效果对比Fig.2 Results contrast under different measurement matrix

图3 为采样率取50%时选用不同测量矩阵的重构效果图，通过图像视觉和PSNR值也可以比较重构图像质量优劣。

图3 相同采样率时各测量矩阵图像重构效果Fig.3 Results contrast under different measurement matrix

2.4 重构算法对重构信号质量的影响

在相同条件下，压缩感知不同重构算法有不同特点，应用时尽量采用效果最优化算法，此处对3种常用的基追踪算法(BP)算法、正交匹配追踪(OMP)算法和阶段正交匹配追踪(StOMP)算法做了对比研究[22-25]。实验中，对256*256的灰度图像“Barbara”进行重构，使用小波对图像进行变换，使用效果比较好速度较快的结构化随机矩阵作为测量矩阵。

(1)相同采样率时各算法的性能比较。实验中设定图像的采样率（M/N）恒为80%时，得到的对比结果如图4所示。由图4可见，3种算法采样率相同时，BP算法重构图像效果最好，OMP重构图像效果较好，而StOMP算法重构图像效果最差。3种算法中，BP算法运行时间最长，StOMP算法运行时间最短。

图4 相同采样率不同算法时的性能比较Fig.4 Results contrast under different algorithms

(2)采用率不同时各算法的性能比较。为了进一步比较各算法的性能，对原始图像在不同采样率情况下重构结果进行了比较，原始图像的采样率（M/N） 分别为 80%、70%、60%、50%、40%、30%时，各算法对应的重构图像效果对比如图5所示。

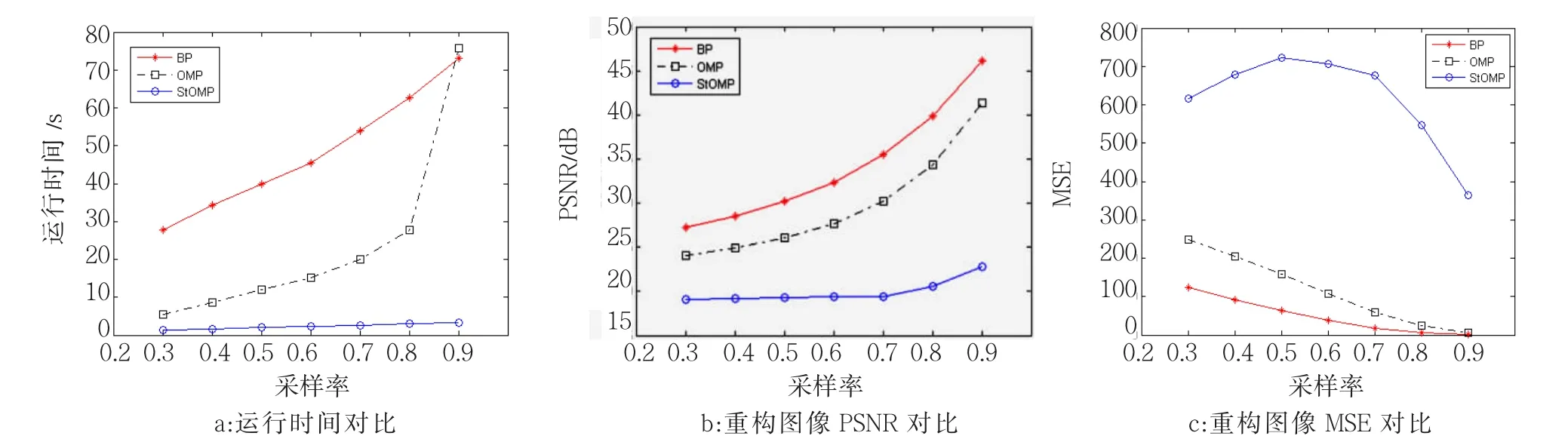
图5 不同算法时图像重构效果Fig.5 Results contrast under different algorithms

由图5可见，3种算法均是随着采样率的增加，重构图像与原始图像的峰值信噪比PSNR增大，如图5b。说明信号的采样率越高，重构图像质量越高，效果越明显。相同采样率下，BP算法重构图像质量最好，StOMP算法重构图像的质量最差；当采用率低于70%时，StOMP算法重构图像的质量基本不变，但效果比较不理想。3种算法下，重构图像和原始图像的均方差总体趋势下都是随采样率的增加而减小；相同采样率条件下，BP算法均方差最大，StOMP算法均方差最小，如图5c。

综合上面所得的结果可知，OMP算法同时能够兼顾重构时间和重构质量，是一种相对比较实用的重构算法。

3 结论

本文研究了应用压缩感知理论进行图像重构的关键技术，分析对比了信号稀疏表示所选取的正交变换基、编码所构造的测量矩阵和重构算法等不同时对重构图像质量的影响。实验结果表明：应用压缩感知理论，仅需30%的采样率即可有效恢复图像，当采样率达到50%时能够获得较高质量的图像，相较于传统图像重构方法中要求采样率至少为原始信号的2倍，大大降低了采样过程中冗余数据过多，信息处理过慢的问题，同时保证了图像信号恢复的质量。

一般情况下，以相对较大的采样率进行采样，使用小波变换基对信号稀疏，以诺斯莱特矩阵作为测量矩阵，以OMP算法进行重构能够有效兼顾图像恢复效率和恢复质量。该研究对当前应用压缩感知理论进行图像处理时在大大降低硬件采集系统的复杂度和耗费成本的前提下，进一步提高重构图像的速度和质量，具有重要的应用意义。

[1]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory，2006，52(4):289-1306.

[2]Candès E J，Romberg J，Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006，52(2):489-509.

[3]Liu X，Yao X，Wang C，et al.Quantum limit of photoncounting imaging based on compressed sensing[J].Optics Express，2017，25(4):3286-3296.

[4]Lu P，Xu Z，Lu X，et al.Digital image information encryption based on compressive sensing and double randomphase encoding technique[J].Optik-International Journal for Light and Electron Optics，2013，124(16):2514-2518.

[5]Sui X B，Chen Q，GU G H，et al.Infrared super-resolution imaging based on compressed sensing[J].Infrared Physics&Technology,2014，63:119-124.

[6]Feng L，Axel L，Chandarana H，et al.XD‐GRASP:Golden angle radial MRI with reconstruction of extra motion state dimensions using compressed sensing[J].Magnetic Resonance in Medicine，2016，75(2):775-788.

[7]Lustig M，Donoho D，Pauly J M.Sparse MRI:The application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine，2007，58(6):1182-1195.

[8]Tavakoli A，Pourmohammad A.Image denoising based on compressed sensing[J].International Journal of Computer Theory and Engineering，2012，4(2):266.

[9]Zhou W P，Li Y，Liu Q S，et al.Fast compression and reconstruction of astronomical images based on compressed sensing[J].Research in Astronomy and Astrophysics，2014，14(9):1207-1214.

[10]Cetin M，Stojanovic I，Onhon O，et al.Sparsity-driven synthetic aperture radar imaging:Reconstruction，autofocusing，moving targets，and compressed sensing[J].IEEE Signal Processing Magazine，2014，31(4):27-40.

[11]Radwell N，Mitchell K J，Gibson G M，et al.Single-pixel infrared and visible microscope[J].Optica，2014，1(5):285-289.

[12]Chen X，Du Z，Li J，et al.Compressed sensing based on dictionary learning for extracting impulse components[J].Signal Processing，2014，96:94-109.

[13]Zhang Y，Dong Z，Phillips P，et al.Exponential wavelet iterative shrinkage thresholding algorithm forcompressed sensing magnetic resonance imaging[J].Information Sciences，2015，322:115-132.

[14]Bigot J，Boyer C，Weiss P.An analysis of block sampling strategies in compressed sensing[J].IEEE Transactions on Information Theory，2016，62(4):2125-2139.

[15]Paleo P，Desvignes M，Mirone A.A practical local tomography reconstruction algorithm based on a known subregion[J].Journal of Synchrotron Radiation，2017，24(1):257-268.

[16]Kher R，Patel Y.Medical image compression framework based on compressive sensing，DCT and DWT[J].Biol，2017，2(2):1-4.

[17]Krzakala F，Mézard M，Sausset F，et al.Probabilistic reconstruction in compressed sensing:algorithms，phase diagrams，and threshold achieving matrices[J].Journal of Statistical Mechanics:Theory and Experiment，2012(8):P08009.

[18]卢佩，田敏，张锐敏.基于IS模型的视觉显著性分析及算法改进[J].石河子大学学报(自然科学版)，2015，33(3):385-390.Lu P，Tian M，Zhang R M.Visual saliency analysis and algorithm advance based on IS model[J].Journal of Shihezi University(Natural Science)，2015，33(3):385-390.

[19]Zhang T，Zhong S，Zhu Z，et al.Reconstruction algorithm based on compressed sensing[J].Journal of Mechanical&Electrical Engineering，2014，31(6):805-818.

[20]程涛.信号重构中测量矩阵性能的判据[J].探测与控制学报，2016，38(4):72-76.Cheng T.Performance criteria of measurement matrices in signal reconstruction[J].Journal of Detection& Control，2016，38(4):72-76.

[21]Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Trans-Actions on Information Theory，2007，53(12):4655-4666.

[22]石光明，刘丹华，高大化，等.压缩感知理论及其研究进展[J].电子学报，2009，37(5):1070-1081.Shi G M，Liu D H，Gao D H，et al.Advance s in theory and application of compressed sensing[J].Acta Electronica Sinica，2009，37(5):1070-1081.

[23]Tan J，Carmon D，Baron D.Signal estimation with additive error metrics in compressed sensing[J].IEEE Transactions on Information Theory，2014，60(1):150-158.

[24]Liu Y，Song T，Zhuang Y，et al.Compressed sensing signal recovery via creditability-estimation based matching pursuit[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2015，98(6):1234-1243.

[25]Massa A，Rocca P，Oliveri G.Compressive sensing in electromagnetics-a review[J].IEEE Antennas and Propagation Magazine，2015，57(1):224-238.

Research on key techniques of image reconstruction based on compressed sensing

Liu Xiaoyong1,Lu Pei2*,Cao Haibing1,Tian Min2
(1 College of Science,Shihezi University,Shihezi,Xinjiang 832003,China;2 College of Information Science and Technology,Shihezi University,Shihezi,Xinjiang 832003,China)

The rapid imaging technology put forward higher demand due to the importance of image application in information,and compressed sensing providesanew way forimageprocessing.Thispaperstudiesthekey technologiesof image reconstruction based on compressed sensing,comparative analysis of the influences on the quality of reconstructed image is emphases.The experimental results show that only 50%of the sampling rate we can obtain high quality images using wavelet transform based on signal sparse,Hadamard matrix as the measurement matrix and orthogonal matching pursuit algorithm.The method availably reduces the redundant data and the visual effects,PSNR values and recovery efficiency of reconstructed image are improved.This research provides a strong basis and support on the theory and technology for the application of compressed sensing to seek optimal image restoration method.

compressed sensing;image reconstruction;sparse signal;measurement matrix;reconstruction algorithm

TP391.41

A

10.13880/j.cnki.65-1174/n.2017.05.020

1007-7383(2017)05-0641-07

2017-02-24

国家自然科学基金项目（61465011）；石河子大学高层次人才项目（RCZX201420、RCZX201436）作者简介：刘效勇(1976-)，男，博士，从事信息安全和三维传感研究,e-mail:llxxyy1017@shzu.edu.cn。

*通信作者：卢佩(1979-),女,副教授,从事信号与信息处理、目标识别研究,e-mail:lupei0@163.com。