基于CFD方法的低速潜航器光体及精细体模型受力计算分析

徐 畅,黄 荐,王亚兴,余 超,王一伟,黄晨光

(1.中国科学院力学研究所流固耦合系统力学重点实验室,北京100190; 2.中国科学院大学工程科学学院,北京100049; 3.中国科学院沈阳自动化研究所,沈阳110016)

基于CFD方法的低速潜航器光体及精细体模型受力计算分析

徐 畅1,2,黄 荐1,2,王亚兴3,余 超1,2,王一伟1,2,黄晨光1,2

(1.中国科学院力学研究所流固耦合系统力学重点实验室,北京100190; 2.中国科学院大学工程科学学院,北京100049; 3.中国科学院沈阳自动化研究所,沈阳110016)

利用CFD计算方法预测潜航器在额定工况下受力一直是工程上的热点问题。通过计算给出实现预期运动所需要的各个推进器提供的静推力,可以为相应的总体方案设计评估和推进器选型提供支撑。利用SST k-ω湍流模型结合笛卡尔网格划分方法,对低速潜航器的光体及精细体模型进行了受力计算,并进行了网格无关性分析。分别比较了两组模型的摩擦阻力及压阻力计算结果,给出了模型表面压力分布、模型周围速度分布及流线形态,并分析了由模型外壳沟槽造成的边界层速度分布变化。

低速潜航器;受力计算;CFD;精细体模型

0 引言

低速潜航器在海洋勘探、海洋工程、水下救助及水下勘测和检测等方面应用广泛,近年来得到了大量的研究发展。用于一般潜水技术不可能达到的深度或区域进行综合考察和研究并能完成多种作业任务的水下机器人,首先要求有较高的航行和作业能力[1-2]。由于要实现全海深覆盖,潜航器也应具备很好的垂直面深度控制与变化能力[3-5]。因而对于低速潜航器的总体方案设计评估和推进器选型而言,受力计算的方法与精度是非常重要的[6-10]。作为一种高效的阻力预报方法,计算流体力学 (CFD)方法在航行器水动力计算方面得到了广泛应用[11-13]。深潜器相对于一般水下航行器来说,外形往往更为复杂,航行器表面存在着大量沟槽及作业设备,因此水动力计算结果与光体模型结果差异较大。如何评估精细体模型与设计中给出的光体模型计算结果之间的差异,分析其带来的影响规律就成为了不可忽视的问题。

本文通过对典型的低速潜航器的水下航行额定工况(水平直航2kn、水平翼角90°的垂直上浮和下潜1kn、水平侧移0.5kn)受力进行计算,分析了光体模型及表面带沟槽的精细体模型的直航阻力计算结果差异。分别通过两组模型表面压力分布、模型周围速度分布及沟槽附近局部速度分布云图,讨论了造成压阻力及摩擦阻力计算结果差异的原因,并给出了不同工况下艇体表面压力分布及流线图。

1 数值计算方法

1.1 控制方程

本文控制方程采用雷诺平均N-S方程(RANS),即将流动变量用平均值与脉动值之和来代替,即:

其中,U=(U,V,W)代表3个方向的速度对时间的平均值,上标 “′”代表脉动值。

连续方程:

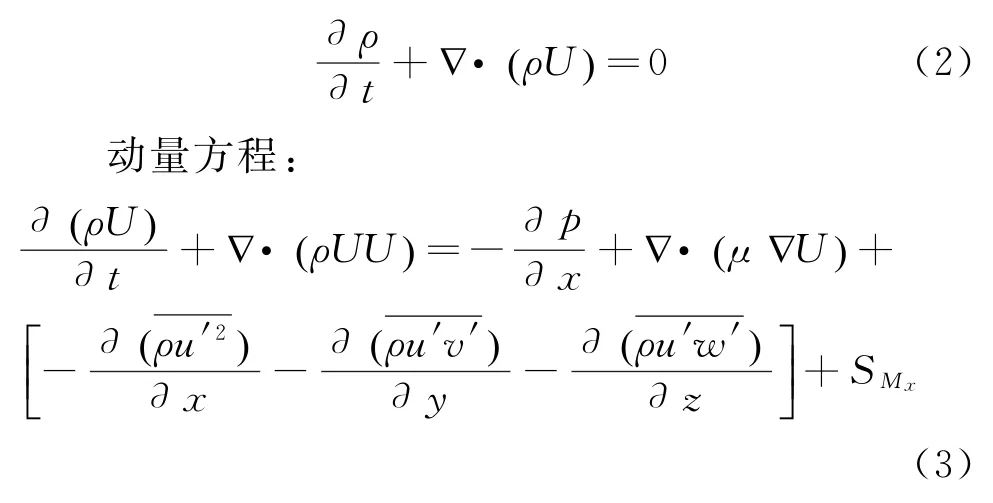
其中,x、y、z表示3个方向,ρ为流体密度, P为压力,t为时间,μ为黏度系数,SMx、SMy、SMz是动量方程的源项。

利用Boussinesq的涡黏假定,引入涡黏性系数μt,建立Reynolds应力相对于平均速度梯度的关系,即Reynolds应力可以表述为:

在应用过程中添加新的变量输运方程,涡黏性系数可以表达为不同变量表达式,FLUENT软件中应用Boussinesq涡黏假定的湍流模型有S-A模型、k-ε模型和k-ω模型,3种模型分别采用不同方法对涡黏系数进行求解[14]。本文中采用SST k-ω湍流模型。

1.2 SUBOFF标模验证

为验证上述方法的正确性,特采用SUBOFF全附体模型进行验证。SUBOFF潜艇主艇体为回转体,艇体总长为4.356m,其中进流段的长度为1.016m,平行中体的长度为2.229m,去流段长1.111m。回转体最大直径为0.508m,特征长度为4.261m[15]。SUBOFF标模的笛卡尔网格划分结果如图1所示,网格数量为192万。在包括指挥台围壳和平衡尾翼等区域进行了网格加密处理。

图1 SUBOFF标模笛卡尔网格划分结果(网格数192万)Fig.1 Cartesian cut-cell mesh of SUBOFF calibration model(cell number 1.92 million)

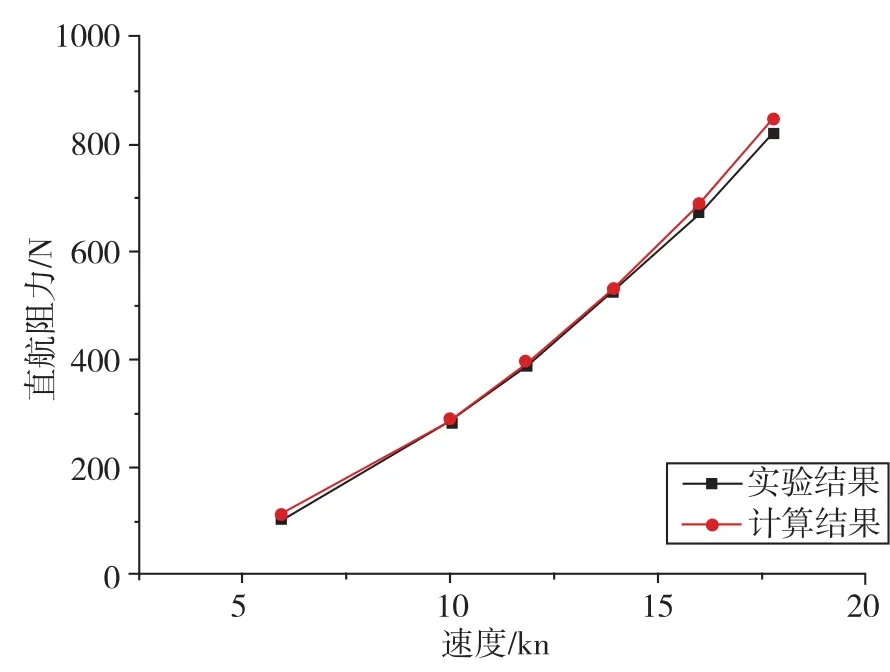
图2 SUBOFF标模直航阻力计算结果与实验对比Fig.2 Comparison between the simulated results and experimental data for SUBOFF calibration model

计算时采用的湍流模型是SSTk-ω模型,压力和速度的耦合采用SIMPLE算法。采用标准方法对压力项进行离散,速度、湍动能和湍动能扩散率等均采用2阶迎风格式进行离散。计算与实验结果比较如图2所示。由图2可以看出,计算结果与实验吻合良好,验证了数值模拟方法的准确性。

1.3 边界条件及网格划分

计算中定义的边界条件包括速度入口、压力出口以及无滑移壁面。整个三维计算域如图3所示,计算域尺寸长为60m,宽和高都为16m。

图3 计算域与边界条件设置Fig.3 Calculation domain and boundary conditions

计算域网格划分时采用了笛卡尔网格方法,对尾部水翼和舵板进行了局部加密,第一层边界层高度为3×10-4m,边界层数15层,总网格量约为585万。网格划分结果如图4所示。

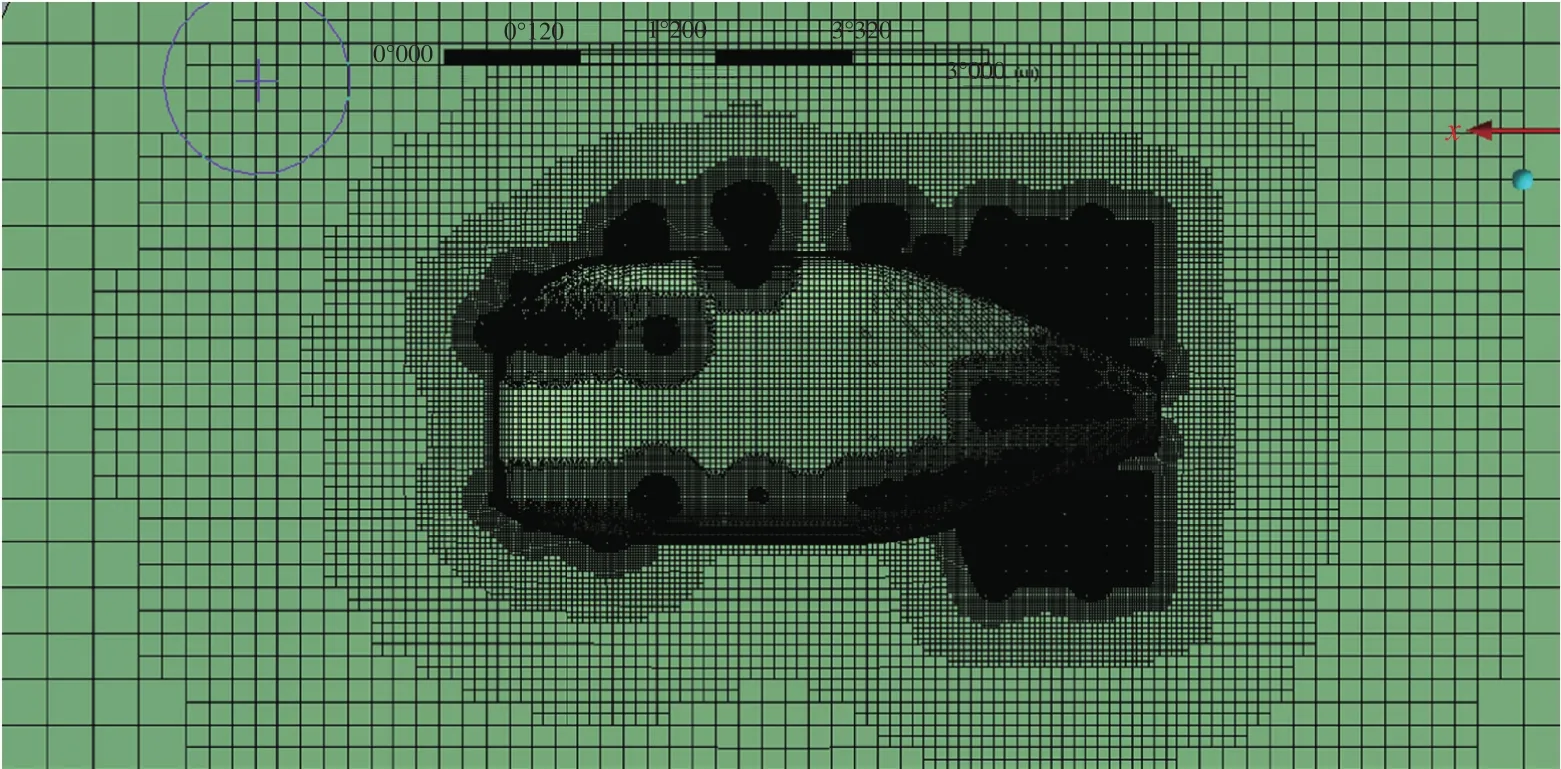
图4 网格划分结果(总网格数585万)Fig.4 Cartesian cut-cell mesh around the underwater vehicle(total cell number 5.85 million)

1.4 网格无关性验证

网格无关性验证中包括了两套网格,一套粗网格的网格数量为180万,划分时同样采用了笛卡尔网格方法,没有对网格进行局部加密,没有添加边界层。网格划分结果如图5所示。

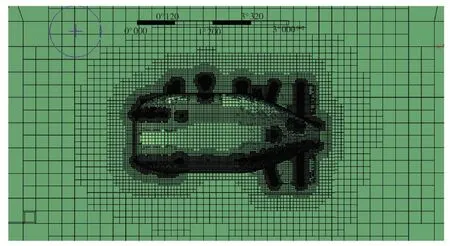
图5 网格划分结果(粗网格,总网格数180万)Fig.5 Cartesian cut-cell mesh around the underwater vehicle(coarse mesh,total cell number 1.8 million)

另一套细网格的网格数量为975万,划分时同样采用了笛卡尔网格方法,并对计算域中间圆形区域及尾部流场进行了加密。网格划分结果如图6所示。

图6 网格划分结果(细网格,总网格数975万)Fig.6 Cartesian cut-cell mesh around the underwater vehicle(refined mesh,total cell number 9.75 million)

验证计算中一共包括3套网格,网格数量分别为180万、585万和975万。计算对直航0.5kn、1kn及2kn的阻力结果进行了对比,结果如表1所示。从表1中可以看出,随着网格数量的增加,计算结果趋于收敛。由于中间网格与细网格计算结果相差很小,因此后续采用了585万网格进行分析计算。

表1 3套不同网格阻力计算结果对比Tab.1 Comparison of the simulated drag of the coarse mesh,original mesh and refined mesh

2 计算结果与分析

2.1 光体模型受力计算

首先计算了水平直航2kn、水平翼角90°垂直上浮和下潜1kn、水平侧移0.5kn这4个工况下航行器各方向受力和力矩情况,结果如表2所示。

表2 直航、垂直上浮及下潜、水平侧移4个工况潜航器光体模型受力和力矩结果Tab.2 Simulated results of the 4 cases for the original model (direct route,vertically float and dive,horizontally side-to-side)

2.2 精细模型受力计算

典型的精细潜航器模型表面分布了3mm沟槽及艇上配件,计算方法与之前相同。整个三维计算域的示意图如图7所示,计算域尺寸约为长60m、宽30m和高40m。网格划分时对尾部水翼、舵板以及模型表面沟槽进行了局部加密,总网格量约为2657万。网格划分结果如图8所示。水翼及沟槽附近局部网格划分如图9所示。

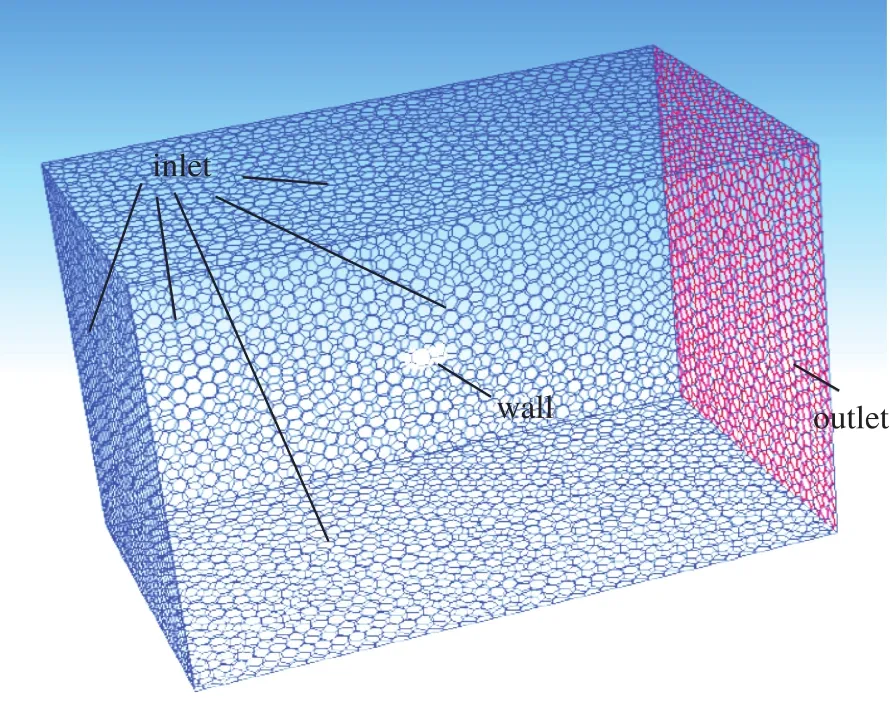
图7 计算域与边界条件设置Fig.7 Calculation domain and boundary conditions

图8 网格划分结果(2657万)Fig.8 Cartesian cut-cell mesh around the underwater vehicle(26.57million)

图9 水翼及沟槽附近局部网格划分图Fig.9 Cartesian cut-cell mesh around the foil and grooves

同样对水平直航2kn、水平翼角90°垂直上浮和下潜1kn、水平侧移0.5kn等4个工况航行器各方向受力和力矩进行计算,结果如表3所示。

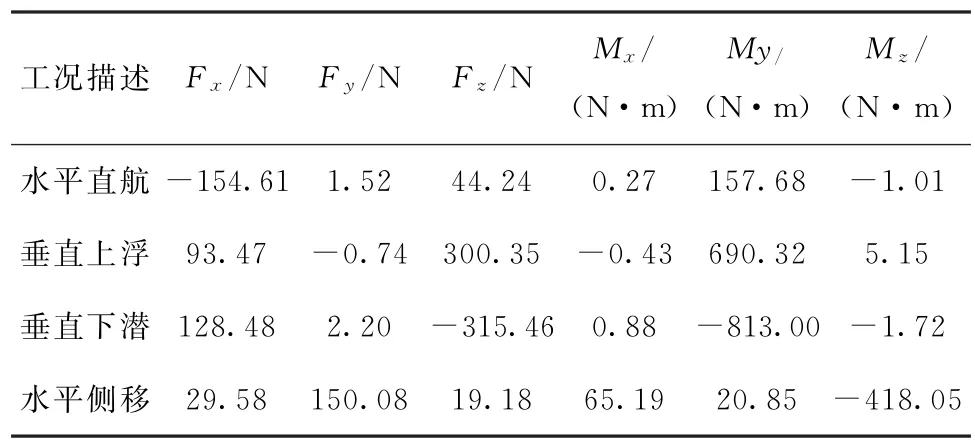
表3 直航、垂直上浮及下潜、水平侧移4个工况潜航器精细体模型受力和力矩结果Tab.3 Simulated results of the 4 cases for the detailed model (direct route,vertically float and dive,horizontally side-to-side)

2.3 不同模型计算结果比较与分析

在详细设计阶段得到的精细体模型与初步设计阶段得到的光体模型相比,计算所需的网格数量显著增多,对计算资源要求较高,计算量较大。光体与精细体模型受力计算结果的差异会影响总体方案设计评估中的推力分配方案设计和推进器选型。按照潜航器所受作用力的方向分类,潜航器阻力包含了摩擦阻力和压阻力两种阻力成分。以水平直航阻力结果为例,表4中比较了光体及精细体模型计算结果中总阻力、摩擦阻力和压阻力的差异。

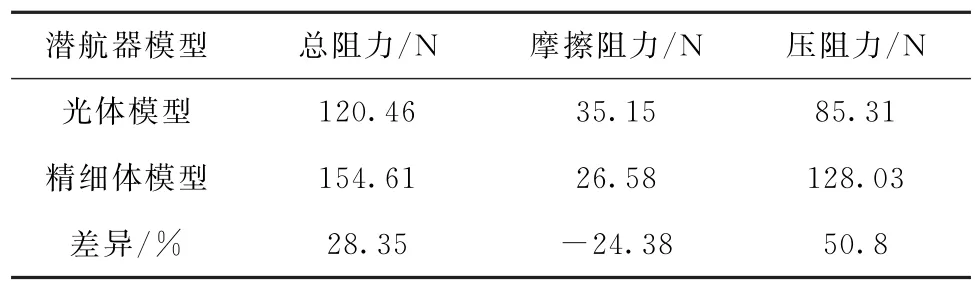
表4 直航2kn工况潜航器光体及精细体模型中总阻力、摩擦阻力和压阻力对比Tab.4 Comparison of the total resistance,frictional resistance and pressure resistance between the original and detailed model of the underwater vehicle

由表4比较结果可以看出,精细体模型总阻力计算结果大于光体模型。其中,精细体模型摩擦阻力计算结果小于光体模型,压阻力计算结果大于光体模型。压阻力计算结果差异较大。图10给出两组计算结果中模型表面的局部压力分布云图,可以看出精细体模型与光体模型相比压力分布更为复杂,模型表面沟槽处压力变化剧烈,因而会造成整体计算结果压阻力大幅增加。

图11对比了潜航器光体及精细体模型周围速度分布云图。由图11可以看出两组模型计算结果中,造成速度分布差异的主要因素是由于精细体模型整体外形与光体相比更为细长,水动力性能更优,因而导致计算结果中精细体模型摩擦阻力较小。图12中精细体模型局部沟槽附近速度分布显示,精细体模型表面存在的沟槽并不会显著改变边界层厚度及其内部的速度分布,因而不会显著影响作用在艇体表面上的切向力,即摩擦阻力。

图10 潜航器光体及精细体模型表面局部压力分布云图(为方便观测,静压显示范围-500Pa~500Pa)Fig.10 Pressure contour charts of the original and detailed model of the underwater vehicle (static pressure display range-500Pa~500Pa for observation)

图11 潜航器光体及精细体模型周围速度分布云图(为方便观测,速度显示范围0m/s~2m/s)Fig.11 Velocity contour charts of the original and detailed model of the underwater vehicle (velocity display range 0m/s~2m/s for observation)

图12 潜航器光体及精细体模型 (沟槽附近)周围局部速度分布云图(为方便观测,速度显示范围0m/s~2m/s)Fig.12 Velocity contour charts near the grooves of the original and detailed model of the underwater vehicle (velocity display range 0m/s~2m/s for observation)

水平直航2kn、水平翼角90°垂直上浮1kn、水平侧移0.5kn的数值计算结果中潜航器模型表面的压力分布及流线图如图13~图15所示。图13中航行器尾部的流线分布很平坦,图14和图15中流线则呈现出明显的旋涡结构,旋涡会增加能量耗散。

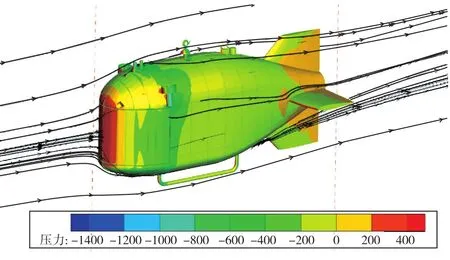
图13 潜航器水平直航2kn模型表面的压力分布及流线计算结果Fig.13 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(direct route 2kn)

图14 潜航器垂直(水平翼角90°)上浮1kn模型表面的压力分布及流线计算结果Fig.14 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(vertically float 1kn)

图15 潜航器水平侧移0.5kn模型表面的压力分布及流线计算结果Fig.15 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(horizontally side-to-side 0.5kn)

3 结论

本文针对潜航器在额定工况下受力问题,利用了SSTk-ω湍流模型结合笛卡尔网格划分方法,对低速潜航器的光体及精细体模型进行了受力计算,并进行了网格无关性分析,得到了较为一致的计算结果。

以水平直航阻力结果为例,比较了光体及精细体模型计算结果中总阻力、摩擦阻力和压阻力的差异。精细体模型总阻力计算结果大于光体模型,精细体模型与光体模型相比压力分布更为复杂,模型表面沟槽处压力变化剧烈,因而会造成整体计算结果压阻力大幅增加。精细体模型表面存在的沟槽并不会显著改变边界层厚度及其内部的速度分布,因而不会显著影响作用在艇体表面上的摩擦阻力。

本文针对全海深ARV设计的关键力学问题开展研究,通过数值模拟手段对航行器的受力特性分析及流动规律进行研究,希望能够支撑工程研制并推动低速潜航器水动力学基础研究的发展。

[1] 朱克强,朱海洋,于春令,等.深海遥控潜水器多体系统非线性耦合动力特性模拟 [J].海洋工程, 2008,26(1):83-87.

[2] 范士波.深海作业型ROV水动力试验及运动控制技术研究[D].上海:上海交通大学,2013.

[3] 封锡盛,李一平.海洋机器人30年[J].科学通报,2013(S2):2-7.

[4] 封锡盛.从有缆遥控水下机器人到自治水下机器人[J].中国工程科学,2000,2(12):29-33.

[5] 封锡盛,刘永宽.自治水下机器人研究开发的现状和趋势[J].高技术通讯,1999,9(9):55-59.

[6] 施生达.潜艇操纵性[M].北京:国防工业出版社,1995.

[7] Gertler M,Hagen G R.Standard equations of motion for submarine simulation[R].Dabid W Taylor Naval Ship Research and Development Center Bethesda MD,1967.

[8] Fureby C,Anderson B,Clarke D,et al.Experimental and numerical study of a generic conventional submarine at 10°yaw[J].Ocean Engineering,2016, 116:1-20.

[9] Shen Z,Wan D,Carrica P M.Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering[J].Ocean Engineering,2015,108: 287-306.

[10] Toxopeus S L,Atsavapranee P,Wolf E,et al. Collaborative CFD exercise for a submarine in a steady turn[C].31stInternational Conference on O-cean,Offshore and Arctic Engineering(OMAE), OMAE2012-83573,2012:761-772.

[11] Stern F,Yang J,Wang Z,et al.Computational ship hydrodynamics:nowadays and way forward[C]. 29thSymposium on Naval Hydrodynamics,2013, 60(1-4):3-105.

[12] Stern F,Wang Z Y,Yang J M,et al.Recent progress in CFD for naval architecture and ocean engineering[J].水动力学研究与进展B辑,2015,27(1): 1-23.

[13] Kim H,Akimoto H,Islam H.Estimation of the hydrodynamic derivatives by Ra NS simulation of planar motion mechanism test[J].Ocean Engineering, 2015,108:129-139.

[14] Pope S B.Turbulent flows[J].Turbulent Flows, 2000,12(11):806.

[15] Roddy R F.Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model(DTRC MODEL 5470)from captive model experiments[R].Ship Hydromechanics Department Departmental Report,David Taylor Research Center,1990.

Force Calculation and Analysis of the Original and Detailed Model of Low-speed Underwater Vehicle Based on CFD Method

XU Chang1,2,HUANG Jian1,2,WANG Ya-xing3,YU Chao1,2,WANG Yi-wei1,2,HUANG Chen-guang1,2
(1.Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China; 2.School of Engineering Science,University of Chinese Academy of Sciences,Beijing 100049,China; 3.Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China)

Force calculation of underwater vehicles based on CFD method is one of the mostly discussed topics within the engineering community.By calculating the required static thrust provided by the various propellers to achieve the desired motion,it is possible to support the corresponding overall design evaluation and propeller selection.In this paper,the SST k-ωturbulence model with the Cartesian cut-cell mesh method is used to calculate the force of the original and detailed model of the low speed underwater vehicle.Moreover,mesh independence study is also carried out.The results show the pressure distribution on the model.The velocity distribution around the model and the result of the streamlines in the flow field are given.Results of the velocity distribution inside the boundary layer around the vehicle caused by the grooves are analysed.

Low-speed underwater vehicle;Force calculation;CFD;Detailed model

TV698.239

A

2096-4080(2017)04-0014-08

2017-9-15;

2017-11-01

国家重点研发计划课题(2016YFC0300802)

徐畅(1992-),女,实习研究员,主要研究方向为空泡流动。E-mail:xuchang@imech.ac.cn