时变干扰下欠驱动AUV水平面轨迹跟踪的反步滑模控制

严浙平,杨泽文,贾鹤鸣,周佳加,王 璐

(1.哈尔滨工程大学自动化学院,哈尔滨150001;2.东北林业大学机电工程学院,哈尔滨150040)

时变干扰下欠驱动AUV水平面轨迹跟踪的反步滑模控制

严浙平1,杨泽文1,贾鹤鸣2,周佳加1,王 璐1

(1.哈尔滨工程大学自动化学院,哈尔滨150001;2.东北林业大学机电工程学院,哈尔滨150040)

针对水下自主航天器AUV水平面的轨迹跟踪问题,建立时变外界干扰条件下的运动学模型以及动力学模型,将地面误差变量转换为艇体坐标变量,并推导得出其误差方程。基于Lyapunov稳定性理论研究反步滑模控制的相关算法,设计出时变干扰下的欠驱动AUV水平面轨迹跟踪控制器,最后分析了闭环控制系统中误差信号受到扰动时跟踪误差的敛散性。利用MATLAB/Simulink软件进行仿真实验,得出时变干扰作用下AUV对期望轨迹的跟踪情况,经实验验证本文设计的反步滑模控制器能有效地跟踪复杂轨迹,具有较强的稳定性和鲁棒性。

欠驱动AUV;轨迹跟踪;反步法;滑模控制

0 引言

水下自主航行器(Autonomous Underwater Vehicle,AUV)是实现海洋科学调查、海下煤油勘探、深水探查和海洋目标探查的重要工具。因其应用范围广,对AUV的深入研究已变成各国深海技术的必要课题[1-6]。研究水下自主航行器的轨迹跟踪控制具有很强的现实意义,但在外界 (如海浪、洋流)干扰的影响下会造成轨迹跟踪的偏离[7-8]。由于实际外界扰动具有时变性,所以在AUV轨迹跟踪控制系统中其抗干扰性就需要着重研究。

近年来,相对于使用PID控制、自适应控制、滑模控制等一些简单的理论,高剑等[9-11]结合几种算法对AUV的水平面轨迹跟踪进行控制。利用粒子群寻优算法,将非线性动力学方程伪线性化,以求解其控制器[12]。Repoulias等[13-14]对水平面航迹跟踪的控制器设计采用反步法以及Lyapunov稳定性相关理论。李欣等[15]对AUV航行角的控制采用了基于灰度预测模糊自适应的控制算法。王一云等[16]在控制算法中加入滤波器,有效解决滑膜变结构控制中常见的颤振现象。

基于上述文献的综述分析,为了进一步提高AUV在时变干扰作用下控制系统的精度和抗扰性能,本文研究欠驱动AUV在水平面的运动规律,并建立其航行误差方程。模拟AUV在实际航行中所受到的干扰问题,基于反步法、滑模控制以及Lyapunov理论设计出有效的控制器,实现对轨迹的精确跟踪,提高轨迹跟踪系统的稳定性和鲁棒性。

1 欠驱动AUV水平面误差方程的建立

在外界的时变扰动下,欠驱动AUV的运动学模型与动力学模型分别如式(1)、式(2)所示。

运动学模型:

其中,x、y和ψ分别是建立在地球坐标系中AUV的位置和艏摇角,u、v、r分别代表AUV在船体坐标系中的纵向速度、横荡速度及艏摇角速度。

动力学模型:

其中,X为纵向作用力,Y为横向作用力,N为偏航力矩。m11=m-X u·,m22=m-Y v·,m33=m-N r·,X u、X u|u|、Y v、Y v|v|、N r、N r|r|为水动力参数。ω1、ω2、ω3为有界时变扰动在AUV运动系各自由度的分量。

为了方便控制器的设计,通过坐标转换将地面误差变量E1(t)=[x e,y e]T转换为船体坐标变量,得到了两个船体坐标位置误差变量E B(t)= [e x,e y]T,并得到完全由期望轨迹表达的期望航向角在地面坐标系下定义位置和姿态误差为:

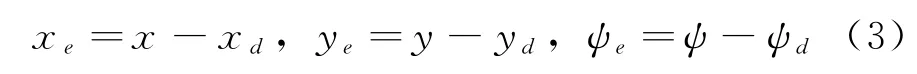
船体坐标下的位置误差公式在坐标转换后表示为:

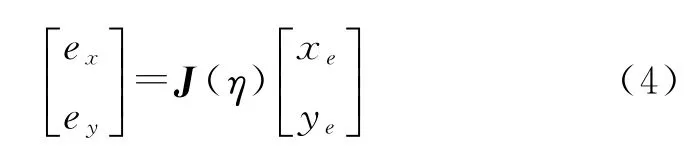
结合式(3)对式(4)求导得水平面误差方程:

2 反步滑模控制器设计

本文中欠驱动AUV水平面轨迹跟踪控制器基于Lyapunov相关理论和反步滑模控制理论(见图1)。

2.1 步骤1

为了使欠驱动AUV的实际位置P(t)跟踪期望的位置P d(t),首先构造Lyapunov函数:

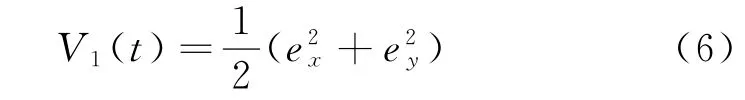
对式(6)求导,同时代入误差方程式(5)可得:

图1 反步滑模控制系统框图Fig.1 System block diagram of backstepping sliding mode control

其中,k1、k2为正常数,

考虑到u d、αd不是真实的可控变量,于是定义误差变量:

结合式(7)和式(8),得到:

2.2 步骤2

构造Lyapunov函数并推导出实际控制力距u1:

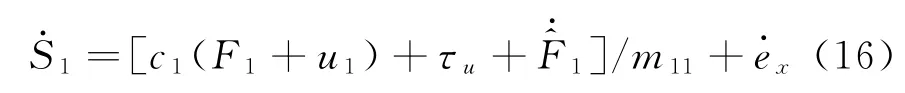
对V2(t)求导可得到:

2.3 步骤3

构造Lyapunov函数:

将式(19)代入式(20)可重新得到:

2.4 步骤4

设计控制器使eα稳定。由式(8)和式(9)可得:

为了使V·3(t)为负,且避免设计r d时在分母中出现cos(ψe),重新定义选取r的期望值为:

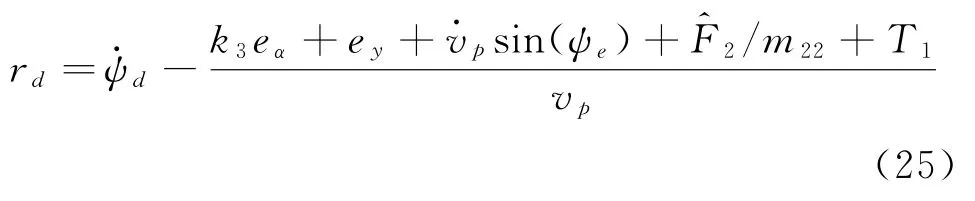
因为rd并非真实的可控变量,定义误差变量:

可以重新得到:

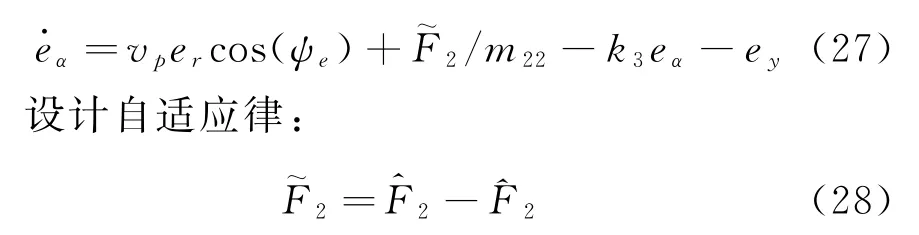
将eα视为虚拟控制输入,构造Lyapunov函数:

对式(29)求导可得:

2.5 步骤5

同理,设计控制器使er稳定:

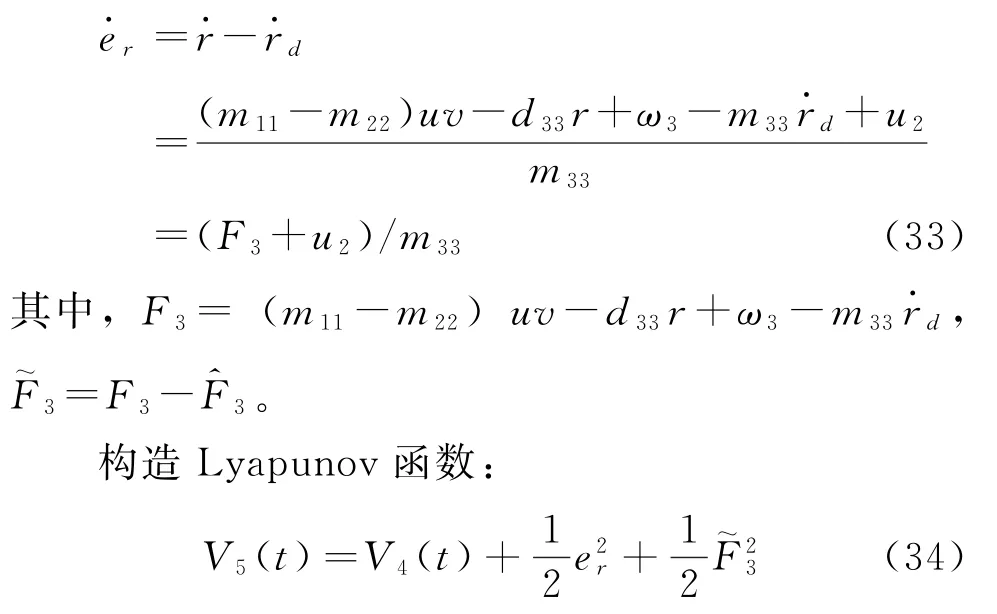
设计滑模函数:

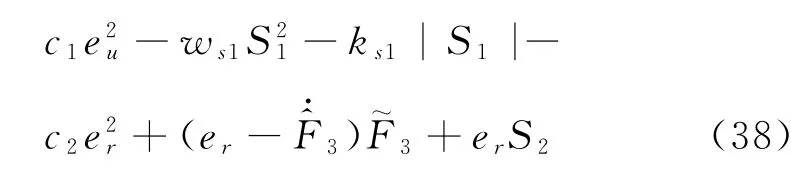
2.6 步骤6

构造Lyapunov函数

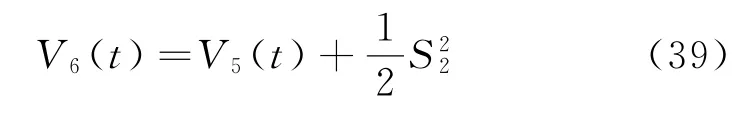
对式(39)求导可得:

最终V6(t)的微分为:

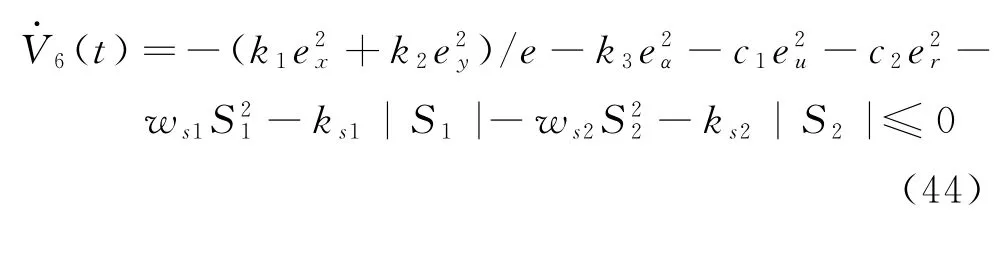
3 稳定性分析

定理:针对欠驱动无人水下航行器的运动学与动力学模型(1)-(2),如果系统采用式(20)和式 (41)的控制力和控制力矩,则闭环控制系统中的误差信号在外界时变扰动下全局一致性是趋于稳定的,且跟踪误差收敛。

证明:定义

其中,γ=min{k1,k2,k3,k4,k5},由于Δ有界,根据Lasalle不变性原理,有:

式(48)表明,跟踪误差z最终收敛到0,即整个AUV闭环跟踪控制系统的全局一致性趋于稳定。

4 时变干扰下反步滑模控制仿真研究

为了验证本文设计的反步滑模控制器是否有效,从实际工程的角度设计了一种 “5”字形的时变轨迹跟踪曲线。所设计的欠驱动AUV水平面轨迹跟踪控制器的MATLAB/Simulink仿真结构图如图2所示。

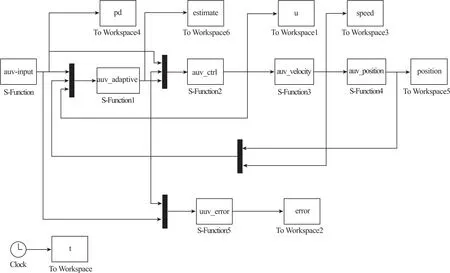
图2 轨迹跟踪控制器Fig.2 Controller of trajectory tracking

为了证明本文设计控制器能够跟踪较复杂的曲线 (即 “5”字形时变轨迹曲线,它包含了直线、半圆和斜线的曲线),以及解决当艏向角误差ψe=±π/2时存在奇异值的情况,在设计平面跟踪时考虑了此种情况。其中半圆部分选取轨迹为:

起始点为(x,y)=(0,160),即选取的初始位置误差为(x e,y e)=(0,-10),第一个直角切换a点选取为(x,y)=(200,150),几个轨迹直角拐点分别选取为:b:(x,y)=(200,100),c: (x,y)=(100,100),d:(x,y)=(100,50)。直线与半圆的切换点分别为e:(x,y)=(150, 50),f:(x,y)=(150,-150)。初始姿态和航速均为0,控制增益为:

Simulink仿真实验的结果如图3~图7所示。外界时变扰动为:

如图3所示,欠驱动AUV的水平面跟踪能完成较复杂的期望轨迹。图4表示各项跟踪的速度误差与角速度误差都足够小,且最终趋于0,其中4个艏向角误差ψe=±π/2也清晰可见,说明本文所提控制方法的有效性和鲁棒性。图5为欠驱动AUV线速度响应曲线和角速度响应曲线,曲线表明即使在角度突变的情况下,速度变化依然较缓,说明所提方法很好地抑制了速度突变的问题,虽然在角度突变时有较大的变化,但依然能实现对跟踪误差的控制。各项位置误差变化可从图6可以看出,曲线较快趋于0。图7为AUV的实际控制输入相应的变化情况。

图3 欠驱动AUV平面“5”字形轨迹跟踪效果图Fig.3 The underactuated AUV trajectory tracking for“5”glyph rendering

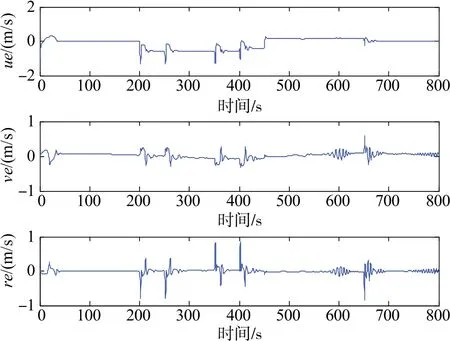
图4 欠驱动AUV轨迹跟踪速度误差响应曲线Fig.4 Response curve of the underactuated AUV trajectory tracking velocity error

图5 欠驱动AUV速度与角速度响应曲线Fig.5 Response curve of the underactuated AUV velocity and angular velocity

从图3~图7可以看出本文所设计的欠驱动AUV反步滑模轨迹跟踪控制器能够实现在外界时变扰动下,对时变平面轨迹的精确跟踪。

图6 欠驱动AUV轨迹跟踪位置误差响应曲线Fig.6 Response curve of the underactuated AUV position error

图7 欠驱动AUV的控制输入Fig.7 Control input of the underactuated AUV

5 结论

本文设计的基于Lyapunov理论以及反步自适应滑模算法的控制器,可以有效抑制外界时变干扰对控制系统的影响,保证了AUV水平面的轨迹跟踪,可以满足期望的工程要求。根据Lasalle不变性原理,验证了误差信号函数在外界时变扰动下全局一致渐近稳定,且跟踪误差收敛至0,说明在该控制律下的闭环控制系统是稳定的。通过MATLAB仿真,验证了AUV能够跟踪直线、半圆和斜线的复杂曲线,各项跟踪的速度与角速度误差很小,并且各项位置误差很快趋于0。因此本文设计的反步滑模控制器具有有效性、稳定性以及鲁棒性,且跟踪误差可以较快地收敛,可以实现在时变干扰下的AUV水平面轨迹跟踪的精确控制。

[1] 赵杰梅.离散非线性系统的预测控制方法研究[D].哈尔滨:哈尔滨工程大学,2013.

[2] 毕风阳.欠驱动自主水下航行器的非线性鲁棒控制策略研究[D].哈尔滨:哈尔滨工业大学,2010: 10-20.

[3] Liu L Q,Dai Y T.3D space path planning of complex environmental underwater vehicle[C].International Joint Conference on Computational Sciences and Optimization,2009:204-209.

[4] 郝燕玲,张京娟.基于遗传算法的AUV三维海底路径规划[J].中国工程科学,2003,5(11):56-60.

[5] Nathan E B.Three-dimensional route planner using A*algorithm application to autonomous underwater vehicles[D].Louisiana State University,2008: 1-15.

[6] 武善杰,郑征,蔡开元.基于行为协同和虚拟目标相结合的无人机实时航路规划 [J].控制理论与应用,2011,28(1):131-136.

[7] 施淑伟,严卫生,高剑,等.常值海流作用下的AUV水平面路径跟踪控制[J].兵工学报,2010 (3):375-379.

[8] 张辉.海洋环境下AUV目标跟踪控制研究[D].哈尔滨:哈尔滨工程大学,2012.

[9] 高剑.自主式水下航行器的建模与自适应滑模控制[D].西安:西北工业大学,2004.

[10] 吴小平,冯正平,朱继懋.模糊PID策略在AUV控制中的应用[J].舰船科学技术,2007,29(1): 95-98.

[11] 曹永辉,石秀华,许晖.水下航行器水平面运动的滑模控制[J].弹箭与制导学报,2005,25(4): 337-338.

[12] 严浙平,张彦超,高鹏,等.水下无人航行器水平面路径跟踪控制方法研究 [J].计算机测量与控制, 2011,19(12):2985-2988.

[13] Repoulias F,Papadopoulos E.Trajectory planning and tracking control design of underactuated AUVs [C].Proceedings of the 2005 IEEE International Conference on IEEE,2005:1610-1615.

[14] Repoulias F,Papadopoulos E.Planar trajectory planning and tracking control design for underactuated AUVs[J].Ocean Engineering,2007,34(11-12): 1650-1667.

[15] 李颀,石秀华,康智强.基于灰色预测的AUV水平面轨迹跟踪控制研究 [J].西安工业大学学报, 2012,32(5):384-387.

[16] 王一云,严卫生,高剑,等.基于滑模变结构控制滤波的水下机器人水平面轨迹跟踪控制 [J].计算机测量与控制,2013,21(2):382-385.

Backstepping Sliding Mode Control of the Underactuated AUV in Horizontal Plane Trajectory Tracking Under the Time-varying Disturbance

YAN Zhe-ping1,YANG Ze-wen1,JIA He-ming2,ZHOU Jia-jia1,WANG Lu1
(1.Harbin Engineering University,College of Automation,Harbin 150001,China;
2.Northeast Forestry University,College of Mechanical and Electrical Engineering,Harbin 150040,China)

According to the AUV(Autonomous Underwater Vehicle)in the horizontal plane trajectory tracking problem,based on time-varying interference the condition of the kinematics model and dynamics model is defined,transforming the ground error variables into hull coordinates,and finding out the error equation.Based on the Lyapunov theory and the algorithm of backstepping sliding mode control,horizontal underactuated AUV trajectory tracking controller in a timevarying interference is designed.Finally,the convergence or divergence of the tracking error in closed loop control system under the error signal disturbance is analyzed.Simulation studies are conducted by MATLAB/Simulink software,and the simulation experiment of AUV on the desired trajectory under time-varying interference is obtained.The experimental results show that the back-step sliding mode controller can effectively track the complex trajectory and has strong stability and robustness.

Underactuated AUV;Trajectory tracking;Backstepping method;Sliding mode control

TP273

A

2096-4080(2017)04-0001-07

2017-09-09;

2017-10-26

国家自然科学基金(51679057);黑龙江自然科学基金(E2017014)

严浙平 (1972-),男,工学博士,教授,研究方向为水下无人航行器的总体设计、智能控制和运动控制。E-mail:yangzewen@hrbeu.edu.cn