基于分子动理论算法的三电平逆变器谐波优化

易灵芝 ，李真贵 ，范朝冬 ，梁湘湘 ，马文斌

（1.智能计算与信息处理教育部重点实验室（湘潭大学），湘潭 411105；2.南车株洲电机有限公司，株洲 412001；3.湖南省“风电装备与电能变换”2011协同创新中心，湘潭 411105）

基于分子动理论算法的三电平逆变器谐波优化

易灵芝1，3，李真贵1，范朝冬1，梁湘湘2，马文斌2

（1.智能计算与信息处理教育部重点实验室（湘潭大学），湘潭 411105；2.南车株洲电机有限公司，株洲 412001；3.湖南省“风电装备与电能变换”2011协同创新中心，湘潭 411105）

在许多大功率交流传动场合下，开关损耗大。为了降低开关损耗，提高逆变器效率，开关频率一般限制在1 kHz以下，导致牵引逆变器中含有大量的谐波。以应用于大功率电力机车的三电平逆变器为特定的研究对象，建立了三电平逆变器最小相电流总谐波畸变率谐波优化模型。采用分子动理论优化算法求解模型时施加了消除窄脉冲算法，完成全调制范围、多种脉波条件下优化函数的求解。与传统SPWM和SHEPWM比较，MMTPWM具有良好的谐波优化效果。最后，通过仿真实验和硬件实验结果验证了理论分析的正确性。

牵引逆变器；谐波优化；分子动理论优化算法；脉宽调制（PWM）；总谐波畸变率

在大功率牵引逆变器中，受较低的开关频率及较高的电机定子频率限制，牵引逆变器在启动后都工作在很低的载频比状态下[1-2]。低载频比工作状态导致逆变器输出电流谐波含量较大、牵引电机附加损耗增加[3-4]。这些谐波会使牵引电机转矩脉动加大，运行温度升高，同时还会产生机械震动和噪声[5]。为了提高逆变器低载频比下的电流输出质量，有必要采用优化正弦脉宽调制SPWM（sinusoidal pulse width modulation）方法来进行牵引逆变器的输出谐波优化，提高其驱动性能[6-7]。

优化PWM是基于目标函数最优值求解的优化调制方法。文献[8]研究了特定谐波消除脉宽调制SHEPWM（selective harmonic elimination PWM）的开关状态求解，其优点是求解时不需要具体的电路参数，优化函数具有通用性。相对于传统的SPWM，SHEPWM在一定调制度以上有更好的电流谐波抑制能力[9]。SHEPWM虽然能消除特定的低次谐波，但其余谐波含量大，输出电流总谐波畸变率THD（total harmonic distortion）较大[10]。文献[11]以最小电流THD为优化目标，对两电平逆变器输出电流THD进行了优化，谐波电流最小同步优化策略比SHEPWM策略具有更好的谐波抑制能力，不足的是该文没有考虑到可能会出现的窄脉冲问题；文献[12]将粒子群智能算法PSO（particle swarm optimization）用于求解复杂的PWM谐波优化问题，取得了较好的效果。在这以后，更多的学者致力于研究智能算法解决PWM优化问题[13-14]。文献[15]首次提出了分子动理论优化算法MMT-OA（optimization algorithm based on molecalar motion theory），经过测试函数的测试，证明了该算法的综合能力优于PSO和神经网络等其他智能算法，能快速且准确地求出最优解，更适合PWM优化问题的求解。

本文以大功率三电平牵引逆变器为研究对象，将MMT-OA应用于PWM问题的求解，建立了最小电流THD谐波优化模型，并施加消除窄脉冲算法。在Matlab仿真实验和硬件实验中验证MMT-PWM方法的谐波优化效果。

1 三电平牵引逆变器电机驱动系统谐波优化模型的建立

1.1 三电平牵引逆变器-电机驱动系统

三电平牵引逆变器-电机驱动系统的主电路结构如图1所示。

可编程优化PWM几乎都是基于1/4周波对称、半波反相的电压波形[16-17]，假定图1中的三电平逆变器输出相电压是1/4周期对称，1/2周期反对称的，如图2所示。由波形的对称性可知，只要确定第1个1/4周期内的N个脉冲开关角度，三电平逆变器的输出电压脉冲序列就能唯一地确定。

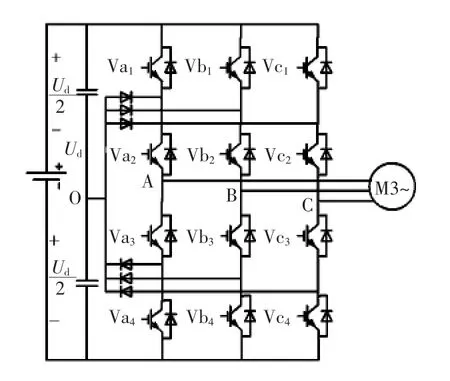
图1 牵引逆变器-电机驱动系统主电路结构Fig.1 Main circuit structure of traction inverter-motor drive system

图2 uao波形Fig.2 Waveform of uao

图2中，A相电压uao的傅里叶变换式为

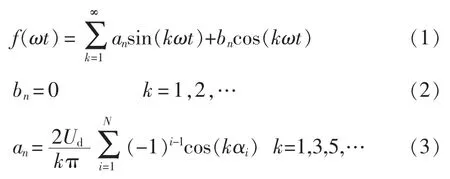
可得uao的表达式为

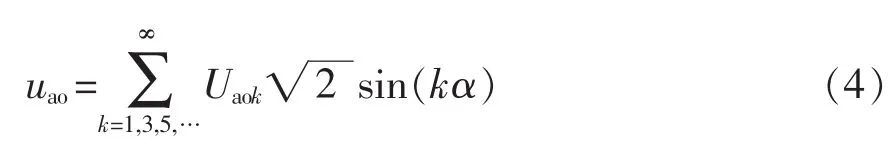
式中Uaok为uao的第k次谐波分量有效值，表示为

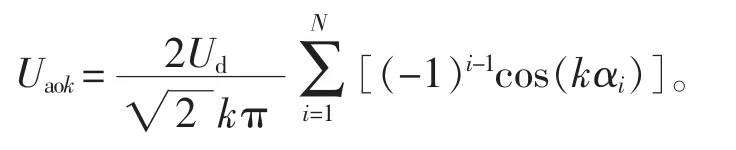
1.2 谐波电流最小优化模型建立

三相电机负载可以等效成一个三相RL网络，相电流的谐波成分由相电压的谐波成分决定。当异步牵引电机基波频率较高时，其k次谐波电流的有效值近似为

式中：Uk为 k次谐波相电压的有效值；Xls、Xlr为基波频率下的定子漏电抗和转子漏电抗。

设异步牵引电机的基波电力为I1，则逆变器输出电流的总谐波畸变率THDi为

根据工程应用的要求，计算THD时最高次谐波取到50次即可。在负载Y型连接对称负载且中心点不接地的情况下，逆变器输出相电压不含有3k次谐波，只含有6k±1次。优化问题可描述如下

1.3 窄脉冲消除方法

在利用MMT算法求解优化PWM问题时，开关角变量的约束条件一般为：0＜α1＜α2＜…＜αN＜π/2，相邻开关角的间距无限定，可能出现较小值，即求得的优化脉冲序列可能包含窄脉冲。窄脉冲会导致开关器件不能正常导通或关断，大大增加开关器件的开关损耗，同时还会影响变流器的输出性能，增加谐波含量。因此，必须采取措施消除窄脉冲。

图3为uao在第1个1/4周期内的波形。根据开关器件的手册数据，开关器件最小脉冲宽度时间可设置为50 μs。当逆变器的输出频率为f1时，最小脉冲宽度所对应的电角度为：δ=2π（50×10-6f1）≈0.000 314 f1rad。

窄脉冲消除方法是在每个脉冲宽度中插入一个最小的脉宽δ[18]，保证每个脉冲的宽度都大于δ，即可避免出现窄脉冲。将脉冲宽度Δαi分解为δ和新变量之和，即：Δαi=δ+βi，i=1，2，…，N。 那么 αi=以 βi代替 αi后，为避免产生窄脉冲，βi应满足的条件为

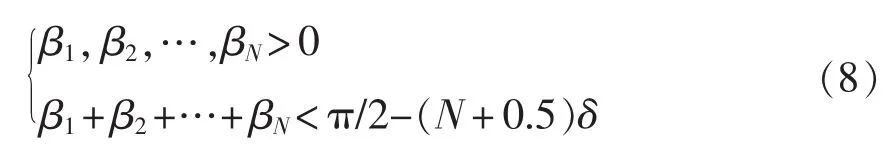
2 MMT-OA及优化模型的条件极值求解

2.1 MMT-OA

MMT-OA是范朝冬博士在受分子热运动启发后于2013年提出来的一种优化算法。分子间存在着相互作用的引力和斥力，分子间引力和斥力随着分子间距离的增大而减小，随着分子间距离的减小而增大，且斥力比引力变化快。

分子引力产生条件：rand＜p1，rand 为 0～1 的随机数。定义引力计算公式为

式中：Fi为个体Xi所受的引力；G为引力常量；Mi和MBest分别为个体Xi和最优个体XBeset的质量。

根据牛顿定理，由式（9）可知，个体Xi的引力加速度αi计算公式为

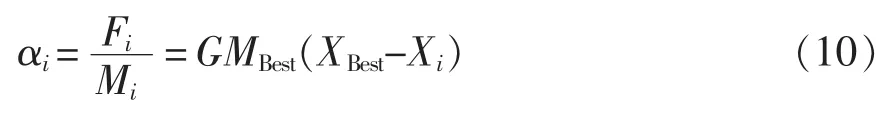
最优个体XBest对Xi产生斥力的条件为：rand＜p2。定义斥力计算公式为

个体Xi的斥力加速度αi计算公式为

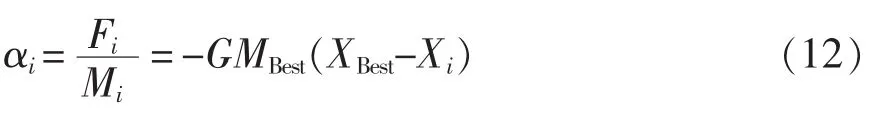
个体的随机扰动加速度定义为

式中：αij为个体 Xi的 j维加速度；pc为变异率，pc∈[0,1]；Xmaxj、Xminj分别为解空间第 j维的上、下界；A为振动幅度，随着温度的降低，振动剧烈程度降低，取其中，t为当前迭代次数，T为总迭代次数；N（0,1）为服从正态分布的随机数。

定义第t+1次迭代时，个体Xi的速度为

第t+1次迭代时，个体Xi的位置为

步骤1初始化。初始化算法参数，生成随机种群，包括种群的初始位置及初始速度。

步骤2计算个体适应值，选出最优个体XBest。

步骤3判断引力产生条件是否满足。如满足，则按式（10）计算引力加速度；否则，判断斥力产生条件是否满足，如满足，则按式（12）计算引力加速度；否则，进行分子热运动操作，按式（13）计算扰动加速度。

步骤4根据式（14）计算个体的速度，并按照式（15）进行个体移动。

步骤5对种群最优个体进行精英保留操作。

步骤6判断算法结束条件是否满足。如不满足，返回步骤2；否则，输出计算结果。

2.2 三电平牵引逆变器电机驱动系统谐波优化模型求解

在脉波数确定后，每个调制比M都对应一组开关角度，这样就可借助Matlab等数学处理工具进行离线数学求解。非线性方程组的收敛点不会太多，可采用大量赋随机初值的方法，结合式（8）的约束条件进行筛选，可以比较顺利地得到符合条件的解。在条件极值求解之时，需要指定调制深度M、开关角个数N，与求解矢量迭代求解初始值α0。从调制输出鲁棒性考虑，开关角对于调制比变化的波形应该具有一点的连续性，因此可将M对应的解αM作为M+ΔM解的初值。

3 仿真研究

根据第2.2小节中的描述的方法，用MMT-OA对第2节中建立的模型进行求解，分子个体数为50个，最大迭代次数T=1 000。图4所示为全调制范围所得到的谐波电流最小MMT-PWM优化开关角和总谐波含量（WTHD）计算结果。图4（a）是9脉波的计算结果，此时N=4，1/4周期内有4个开关角，且载频比为2N+1，由图可知求得的开关角符合式（7）的约束条件，并且没有出现两个开关角特别相近的情况，满足式（8）中的约束条件，没有出现窄脉冲。图 4（b）～（d）分别为 11、13、15 脉波的计算结果。

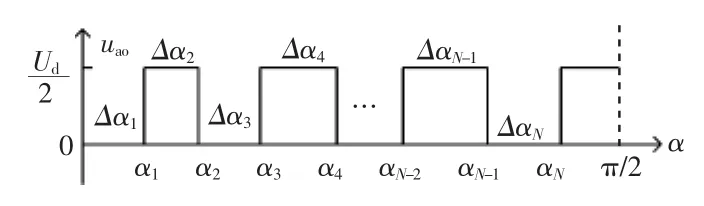
图3 ua0在[0,]内的波形Fig.3 Waveform of ua0among[0,]

图4 全调制范围计算结果Fig.4 Full modulation range results

9脉波、11脉波、13脉波、15脉波WTHD计算结果如图5所示。由图5可知：当调制比M在0～0.5之间变化时，逆变器输出电流的WTHD逐渐减小且减小的幅度很大；调制比M在0.5～1.1附近变化时，输出电流的WTHD变化不同，但整体处于较低的水平；当调制比M在1.1～2变化时，逆变器输出电流的WTHD都增加且增大的幅度比较大。比较图5中N取不同值的结果还可知，在调制比M较小时，开关角个数N越大，WTHD越小，且N为奇数时性能优于偶数时。当开关角确定时优化波形WTHD存在最小点，随着开关键个数的增加，最小点对应的WTHD值逐渐减小，但减小的幅度越来越不明显。同时该点对应的调制比M也有逐渐减小的趋势。针对这一特点，在变流系统工作在较小载频比时，尽量通过各种手段使得系统工作在WTHD最小点附近，可充分利用其谐波抑制性能。

为验证MMT-PWM方法的谐波优化效果，在Matlab/Sinmulink平台搭建了三电平牵引逆变器-电机驱动系统的仿真模型，仿真时间0.2 s。仿真采用的负载为大功率电力拖动系统，其额定有功功率P=2.5×103 kW，电动机额定电压UL=6 kV，功率因子 cos α=0.86。 求得其等效阻抗为：R=10.4 Ω，L=20.5 mH。牵引逆变器直流侧电压Ud=6 kV。以一个工作点f1=50 Hz、M=4、N=7为例，开关角取值如表1所示，对比传统PWM和MMT-PWM两种方法控制下牵引逆变器的输出电流，波形如图6所示，由图可见，与SPWM方法相比，采用MMT-PWM方法得到的电流THD明显降低。

图5 9、11、13、15脉波 WTHD 计算结果比较Fig.5 WTHD comparison among 9，11，13，15 pulses

表1 开关角取值Tab.1 Switching angle values

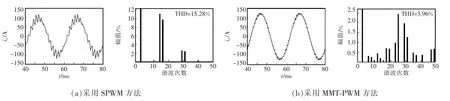
图6 2种PWM方法输出电流THD比较Fig.6 Output current THD comparison of two methods of PWM

文献[18]采用PSO算法对三电平逆变器输出谐波进行优化，文献[11]中给出了15脉波情况下采用SHEPWM方法得到的输出相电流THD。结合这两篇文献，3种方法的仿真结果对比如表2所示。SHEPWM方法虽能消除低次谐波，但其余的谐波含量较大。本文以THD为优化目标而不是特定的谐波，所以会比SHEPWM得到的THD更低。由表2可知，MMT-PWM得到的电流波形更接近正弦波，验证了该方法具有良好的谐波优化效果。

表2 3种方法的性能比较Tab.2 Performance comparison among algorithms of MMT-PWM,PSO-PWM and SHEPWM

4 实验验证

在实验室条件下，以一台额定频率为50 Hz的1.5 kW鼠笼式异步电机作为实验对象，该电机的定子电压为380 V，功率因数为0.79，采用三电平逆变器，DSP控制器选用TMS320F2812，将第3节中求得的结果制成表格，当给定电压基波幅值时就可确定调制比M，查表可得到该时刻的开关角取值。直流母线电压620 V，给定电压基波幅值为375 V，基波频率50 Hz，验证15脉波下PWM调制策略和MMT-PWM调制策略相电流波形。

图7为示波器测得的硬件实验波形，图7（a）为采用PWM策略下相电流输出波形，THD=20.32%，图7（b）为采用MMT-PWM调制策略下相电流输出波形，THD=4.97%。采用SPWM方法和MMT-PWM方法时相电压输出如图8所示。由图可见，硬件实验与仿真实验结果吻合，与理论分析一致。验证了所提出MMT-PWM策略的优化效果。

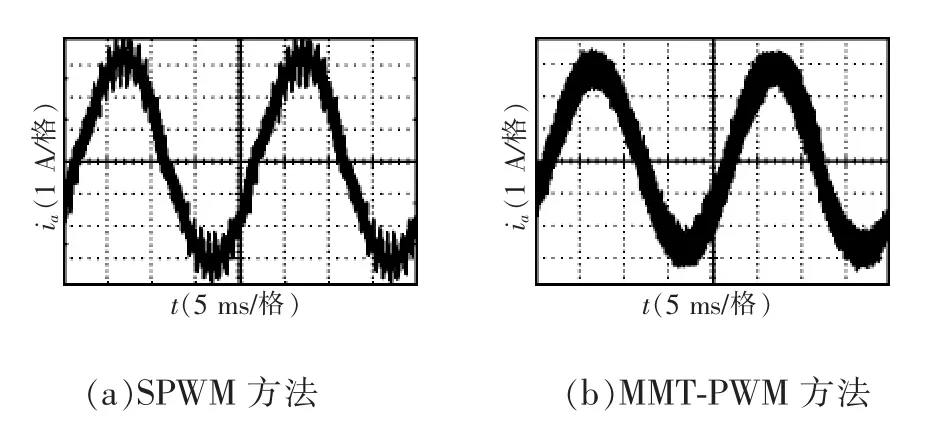
图7 谐波优化效果的实验对比Fig.7 Experimental comparison of harmonic optimization effect

图8 2种方法相电压输出对比Fig.8 Output voltages comparison of two methods of PWM

5 结语

针对大功率场合下电流谐波抑制问题，本文将分子动理论优化算法应用于优化PWM问题的求解，提出一种MMT-PWM优化方法，同时考虑窄脉冲的问题，求出了全调制范围的最优开关角。仿真和实验结果表明，所提出的优化方法能有效减少相电流中的谐波含量。此方法也可用于其他变频装置的谐波优化。

[1]Schweizer M,Friedli T,Kolar J W.Comparative evaluation ofadvanced three-phase three-levelinverter/converter topologies against two-level systems[J].IEEE Transactions on Industrial Electronics,2013,60（12）:5515-5527.

[2]唐凡森,林辉品,王鹿军,等.电网谐波背景下风电并网逆变器的PR I控制方法[J].电源学报,2015,13（4）:8-14.Tang Fansen,Lin Huipin,Wang Lujun,et al.PRI control methodology for wind power grid-connected inverters in harmonic distorted grid utility[J].Journal of Power Supply,2015,13（4）:8-14（in Chinese）.

[3]乐胜康,宋文祥,姜书豪,等.异步电机低开关损耗的模型预测直接转矩控制[J].电源学报,2016,14（5）:68-75.Le Shengkang,Song Wenxiang,Jiang Shuhao,et al.Model predictive direct torque control for low switching losses control of induction motor[J].Journal of Power Supply,2016,14（5）:68-75（in Chinese）.

[4]Zhang Zhaoyang,Feng Xiaoyun,Xu Junfeng.Closed-loop control of PMSM based on optimal synchronous pulse patterns[C].IEEE Electronics and Application Conference and Exposition（PEAC）,Shanghai,2014:687-692.

[5]Liu Shengxue,Sheng Yifa.Efficiency optimization of IPMSM for urban rail traction based on switching frequency optimization control[C].IEEE Control Conference,2011:1997-2001.

[6]Bruzzese C.Minimization of harmful cage torsional resonances in traction motors by a combined mechanic-electronic optimization[C].IEEE Power Electronics and Drives,2009:1-7.

[7]刘斌,薛毓强.消除偶次谐波的三电平NPC逆变器调制方法[J].电力系统及其自动化学报,2011,23（1）:80-85.Liu Bin,Xue Yuqiang.Even order harmonic elimination method of three-level neutral point clamped inveter[J].Proceedings of the CSU-EPSA,2011,23（1）:80-85（in Chinese）.

[8]Maswood A I,Rashid M H.Input current harmonic reduction in high power AC/DC rectifiers[C].Proceedings of the Industrial Electronics,Control and Instrumentation.1991:593-599.

[9]Martinez C,Lazaro A,Quesada I,et al.THD minimization for railway applications through harmonic spectrum optimization[C].Proceedings of the Applied Power Electronics Conference and Exposition（APEC）.IEEE,2012:1609-1614.

[10]黄瀚,纪延超,张辉,等.优化特定消谐PWM技术[J].中国电机工程学报,1997,17（5）:344-347.Huang Han,Ji Yanchao,Zhang Hui,et al.The optimal technique for selected harmonics elimination[J].Proceedings of the CSEE,1997,17（ 5）:344-347（in Chinese）.

[11]马逊,李耀华,葛琼璇,等.谐波电流最小同步优化脉宽调制策略研究[J].中国电机工程学报,2015,35（5）:1211-1220.Ma Xun,Li Yaohua,Ge Qiongxuan,et al.Research on synchronous minimum harmonic current optimized pulse width modulation strategies[J].Proceeding of the CSEE,2015,35（5）:1211-1220（in Chinese）.

[12]娄慧波,毛承雄,陆继明,等.基于微粒群算法的三电平正弦脉冲宽度调制开关时刻优化[J].中国电机工程学报,2007,27（33）:108-112.Lou Huibo,Mao Chengxiong,Lu Jiming,et al.Optimum SPWM switching pattern for three level voltage inverter usingparticleswarmoptimization[J].Proceedings of the CSEE,2007,27（33）:108-112（in Chinese）.

[13]江志平,钱苗旺.基于粒子群算法的三相PWM整流器H2/H∞混合控制研究[J].华东电力,2013,41（12）:2479-2483.Jiang Zhiping,Qian Miaowang.Mixed H2/H∞control of three-phase PWM rectifier based on particle swarm optimization algorithm[J].East China Electric Power,2013,41（12）:2479-2483（in Chinese）.

[14]伏祥运.基于改进PSO算法的优化特定消谐PWM技术[J].东北电力技术,2009,30（2）:7-9.Fu Xiangyun.Optimization of selective harmonic elimination PWM technology based on improved PSO algorithm[J].Northeast Electric Power Technology,2009,30（2）:7-9.（in Chinese）

[15]Fan Chaodong,Ouyang Honglin,Zhang Yingjie,et al.Optimization algorithmbased on kinetic-molecular theory[J].Journal of Centr al South University,2013,20（12）:3504-3512.

[16]Grahame D,Holmes T A L.Pulse width modulation for power converters:principles and practice[M].New Jersey:A John Wileyamp;Sons,Inc.Publication,2002.

[17]Holtz J,Krah J O.Adaptive optimal pulse-width modulation for the line-side converter of electric locomotives[J].IEEE Transactions on Power Electronics,1992,7（1）:205-211.

[18]周伟,韩坤,王顺亮,等.一种消除窄脉冲的三电平粒子群优化PWM方法[J].电力电子技术,2015,49（3）:22-24.Zhou Wei,Han Kun,Wang Shunliang,et al.A three-level PSO-PWM method of narrow pulse elimination[J].Power Electronics,2015,49（3）:22-24（in Chinese）.

易灵芝

易灵芝（1966-），女，通信作者，硕士，教授，研究方向：交流调速与电力电子装置，新能源发电与直流微网等，E-mail：ylz wyh@xtu.edu.cn。

李真贵（1990-），男，硕士研究生，研究方向：电力电子变换，E-mail：zhengui426@qq.com。

范朝冬（1984-）， 男， 博士，讲师，研究方向：智能优化，E-mail：ylzwyh@xtu.edu.cn。

梁湘湘（1978-），男，本科，高级工程师，研究方向：新型功率变换器，E-mail：ylz wyh@xtu.edu.cn。

马文斌（1989-），男，硕士，工程师，研究方向：变压器，E-mail：ylzwyh@xtu.edu.cn。

Optimization of Phase Current Harmonic for Three-level Inverter Based on MMT-OA

YI Lingzhi1,3,LI Zhengui1,FAN Chaodong1,LIANG Xiangxiang2,MA Wenbin2
（1.Key Laboratory of Intelligent Computing and Information Processing （Xiangtan University）,Ministry of Education,Xiangtan 411105,China;2.CSR Zhuzhou Electric Motor Co.Ltd,Zhuzhou 412001,China;3.Wind Power Equipment and Power Conversion 2011 Collaborative Innovation Center,Xiangtan 411105,China）

On high-capacity AC drivers,the switching frequency is limited to a certain level,typically below 1 kHz,in order to reduce switching loss.Due to that,traction inverter output waveforms contain a lot of harmonics.The mathematical model of an optimal pulse width modulation（PWM） method is built,total harmonic distortion（THD） of phase currents is constituted focusing on the three-level inverter used on the high power electric locomotive.The narrow pulse elimination algorithm is applied while using optimization algorithm based on molecalar motion theory MMT-OA to solve the model.The solution of the optimization function on whole modulation range in various pulse wave is completed.MMT-PWM has a good result of harmonic optimization compared with sinusoidal pulse width modulation（SPWM）method and selective harmonic elimination PWM SHEPWM method.All design thoughts and theoretical are verified by emulation and experiment.

traction inverter;harmonic optimization;optimization algorithm based on molecular motion theory（MMT-OA）;pulse width modulation（PWM）;total harmonic distortion（THD）

10.13234/j.issn.2095-2805.2017.6.101

TM464

A

2015-12-21；

2016-04-01

国家自然科学基金资助项目（61572416）；湖南省自然科学基金资助项目（2016JJ5033）

Project Supported by National Natural Science Foundation of China（61572416）;Hunan Provincial Natural Science Foundation（2016JJ5033）