弱电网下基于加权系数的电网电压前馈控制策略

李 明，张 兴，杨 莹，赵文广

（合肥工业大学电气与自动化工程学院，合肥230009）

弱电网下基于加权系数的电网电压前馈控制策略

李 明，张 兴，杨 莹，赵文广

（合肥工业大学电气与自动化工程学院，合肥230009）

在含有电网电压背景谐波以及电网阻抗变化情况下，并网逆变器的控制性能会受到影响。直接电网电压比例前馈因其实现方便且可有效抑制电网背景谐波而获得广泛关注，但其在高电网阻抗的弱电网情况下会降低电流控制的相位裕度，影响并网稳定性。基于加权系数的电网电压前馈控制策略存在基波增益下降的问题，但是能够大幅提高并网逆变器的稳定性。首先，对并网逆变器进行数学建模，并结合阻抗稳定性判据全面对比分析了弱电网下基于加权系数的电网电压前馈控制策略和传统直接电网电压前馈控制策略的动、稳态性能，得出了前者在弱电网下具有更好的电网适应性；其次，给出了调整系统闭环增益的方式来提高并网逆变器基波跟踪性能的理论分析；最后，结合Matlab/Simulink仿真和实验，进一步验证了弱电网下基于加权系数的电网电压前馈控制策略的有效性。

并网逆变器；电网阻抗；弱电网；电网电压前馈；加权系数

随着分布式发电系统的迅速发展，并网逆变器得到了广泛应用。由于偏远地区的分布式发电系统中长距离传输线以及大量变压装置的存在，给电网带来一个不可忽略的等效阻抗，使得电网呈弱电网特性[1-3]。在高阻抗的弱电网情况下，并网逆变器与电网之间会形成一个动态的互联系统，在其公共耦合点PCC（point of common coupling）会造成并网逆变器控制系统带宽下降，影响其控制稳定性[4-7]。

许多学者采用不同的分析方法研究了弱电网下控制系统的稳定性、鲁棒性和抗干扰性。文献[8]指出电网阻抗变化将会影响逆变器控制系统性能和运行稳定性，提出采用配置阻尼的方式来抑制谐振；文献[9]根据逆变器的输出阻抗与电网阻抗之比判断系统的稳定性，提出了阻抗稳定性判据；文献[10,11]均提出了通过调整控制器参数的自适应控制策略。然而，上述文献针对弱电网下的控制策略均仅考虑了电网阻抗的变化，并未考虑弱电网下PCC处的电网电压背景谐波的影响[12]。针对该问题，直接电网电压比例前馈因为实现方便且可有效抑制电网背景谐波而获得广泛关注[13]，但是其在电网阻抗较高即弱电网下，电网电压直接比例前馈控制会降低电流控制的相位裕度，影响并网稳定性[5]。文献[14]提出可以通过调整电网电压前馈比例系数来保证逆变器并网稳定性，并给出了弱电网下的电网电压前馈比例系数的稳定运行边界，文献[15]在上述的研究基础上，分析了采样延时对基于加权系数的电网电压前馈控制策略的影响。然而，上述文献均未指出该方法存在的并网逆变器基波增益大幅降低，不利于基波跟踪的问题。

本文在上述研究的基础上，首先对并网逆变器进行数学建模，并结合阻抗稳定性判据，全面对比分析了弱电网下基于加权系数的电网电压前馈控制策略和传统直接电网电压前馈控制策略的动稳态性能，得出了前者在弱电网下具有更好的电网适应性；其次，给出了通过调整系统闭环增益的方式来提高并网逆变器基波跟踪性能的理论分析；最后，结合Matlab/Simulink仿真和实验，进一步验证了弱电网下基于加权系数的电网电压前馈控制策略的有效性。

1 LCL型并网逆变器

三相LCL型滤波并网逆变器拓扑结构，由三相桥式逆变拓扑、逆变器侧电感L1、滤波电容C和网侧电感L2组成，如图1所示。其中：Udc为直流母线电压，Cdc为直流母线电容，iga、igb、igc为逆变器输出并 网 电 流 ，ega、egb、egc为 电 网 电 压 ，upcca、upccb、upccc为PCC电压（用于电网前馈补偿及锁相），rg、Lg构成电网阻抗Zg[8]，表示为

本文以三相LCL型并网逆变器为例，其额定参数和控制参数如表1所示。

图1 三相LCL型并网逆变器拓扑结构Fig.1 Topological structure of three-phase grid-connected LCL-filtered inverter

2 弱电网下基于加权系数的电网电压前馈控制策略

2.1 基于开环传递函数的稳定性分析

图2为所提出的基于加权系数电网电压前馈控制策略的控制框图，其基本原理是通过设置并网电流参考值与其反馈值作差，然后经过电流环PI调节器模块，并加上电网电压前馈环节反馈的公共耦合点电压，经过延时环节模块，对LCL型并网逆变器主电路进行控制，实现逆变器并网电流跟踪给定值。由于电网阻抗的存在，会引入一条正反馈通道，影响了并网逆变器在弱电网下的稳定性。

图2 基于加权系数的电网电压前馈控制策略控制框图Fig.2 Control block diagram of grid voltage feedforward control strategy based on weighting coefficient

图2 中，igref（s）为并网电流给定值，Gi（s）为电流PI调节器，表示为

式中，kp和ki分别为调节器的比例和积分系数。

Gd（s）为延时环节，表示由于数据采样和控制器造成的延时，即

式中，Ts为采样周期。

Kpwm表示 PWM 逆变环节增益，Gf（s）为电网电压前馈环节，表示为

式中，Kf为电网电压前馈加权比例系数。Kf=1表示传统的直接电网电压前馈控制策略。

根据图 2，igref（s）至 ig（s）的开环传递函数 Go（s）即

由于电网电感是引起并网逆变器在弱电网下稳定性下降的主要原因[14]，因此为了考虑最恶劣情况，本文中考虑纯电感情况的影响。

根据表1的参数，图3（a）给出电网阻抗Lg=0、Kf=1，即强电网下采用传统直接电网电压前馈控制时的开环传递函数Bode图。由图3（a）可见，逆变器的相位裕度 PM（phase margin）为 70°，逆变器能够稳定并网运行，并且稳定裕度较高。图3（b）给出了 Kf=1、Lg分别为 1.2、2.4、3.6 mH， 即弱电网下采用传统直接电网电压前馈控制时的开环传递函数Bode 图。 根据图 3（b）可知，Lg分别为 1.2 mH、2.4 mH和3.6 mH对应的相位裕度依次为37°、19°和14°，可见随着电网阻抗的增大，并网逆变器的相位裕度逐渐下降，并网逆变器的稳定性逐渐下降，其并网电流质量受到影响。

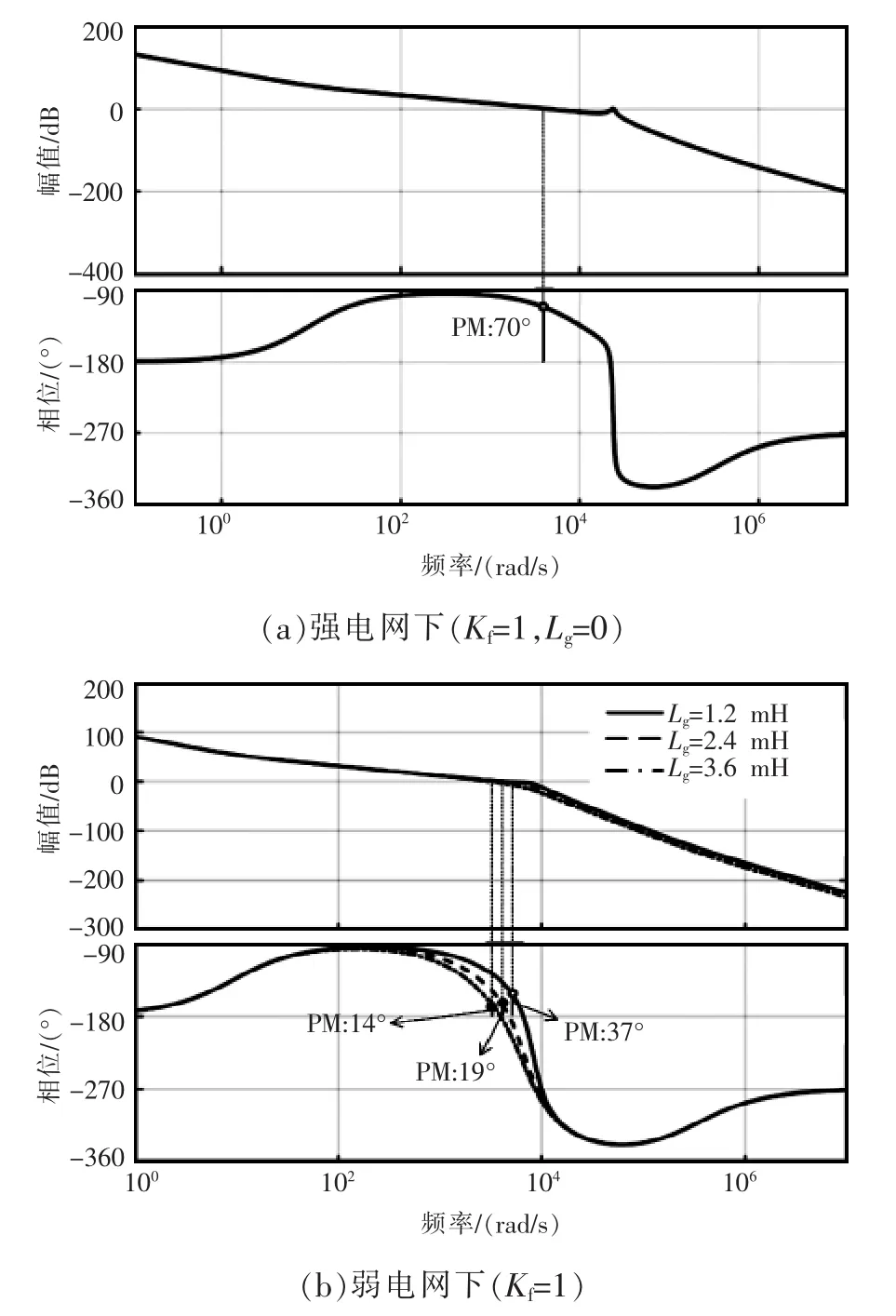
图3 采用直接电网电压前馈控制时的开环传递函数Bode图Fig.3 Bode plots of open-loop transfer function with direct voltage feedforward control strategy

图 4（a）给出了 Kf=0.7、Lg分别为 1.2、2.4、3.6 mH时，即弱电网下采用基于加权系数的电网电压前馈控制时的开环传递函数Bode图，与图3（b）对比可见，采用基于加权系数的电网电压前馈控制时，Lg分别为1.2、2.4、3.6 mH时对应的相位裕度依次为62.7°、63.2°和 65.5°，并网逆变器在弱电网下的相位裕度得到了大幅提升，保证了并网逆变器的稳定性。结合第2.2节中对并网逆变器系统的闭环传递函数根轨迹分析发现，当电网阻抗在一定范围内时，随着电网阻抗的增大，相位裕度逐渐增大，即此时采用基于加权系数的电网电压控制策略时，其相位裕度会随着电网阻抗的增大而逐渐增大；而当电网阻抗过大时，采用基于加权控制的并网逆变器控制策略时，并网逆变器的稳定性同样会随着电网阻抗的增大而下降。

图 4（b）给出了 Lg=1.2 mH，Kf分别为 0.6、0.7、0.8时对应的开环传递函数Bode图。由图4（b）可见，采用基于加权系数的电网电压控制策略时，Kf分别为0.6、0.7、0.8 时对应的相位裕度依次为67.1°、62.6°和56.5°，并网逆变器的相位裕度随着加权前馈系数的降低，相位裕度逐渐增大，表明其并网稳定性上升。并且，随着加权系数的降低，幅频响应曲线与0 dB线的交截频率逐渐减小，表示逆变器控制系统的带宽在逐渐下降，其快速性受到影响。

图4（c）为图4（b）在基波频率处幅频响应曲线的放大图，根据图4（c）可见，采用基于加权系数的电网电压前馈控制时，Kf分别为0.6、0.7、0.8时对应的基波增益依次为18.7 dB、19.4 dB和20.2 dB，因此，随着加权前馈系数的降低，并网逆变器的基波增益在逐渐下降，基波跟踪性能下降。通过调整系统闭环增益的方式来提高并网逆变器基波跟踪性能，其主要方式是增大PI调节器的比例和积分参数来增大系统基波处的开环增益。

本文以Kf=0.8时的基波增益为基准值，设PI调节器的比例和积分参数为1 p.u.；当Kf=0.7时，可以增大PI调节器的比例和积分参数为1.1 p.u.；当Kf=0.6时，增大PI调节器的比例和积分参数为1.2 p.u.，此时得到如图4（d）在基波频率处幅频响应曲线的放大图。对比图 4（c）和图 4（d）可见，通过增大PI调节器的比例和积分参数，可以提高基于加权系数的电网电压前馈控制的基波增益，降低并网逆变器的稳态跟踪误差。

图4 基于加权系数的电网电压控制策略时的开环传递函数Bode图Fig.4 Bode plot of open-loop transfer function with feedforward control strategy based on weighting coefficient

2.2 基于闭环传递函数的稳定性分析

根据图 2，igref（s）至 ig（s）的闭环传递函数 Gcl（s）为

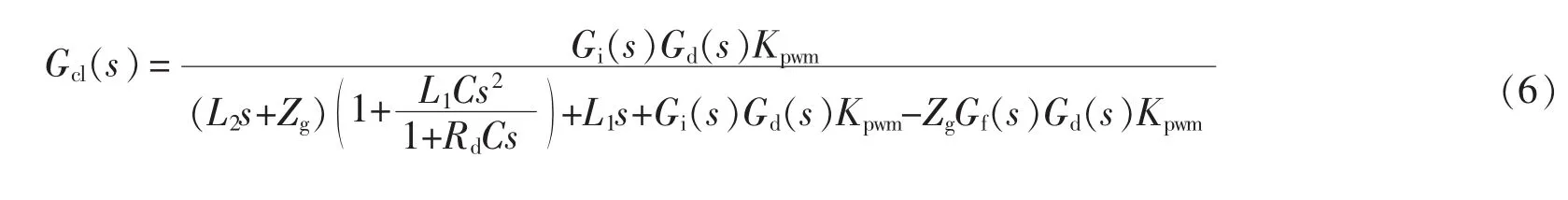
如图5所示为闭环传递函数Gcl（s）随着电网阻抗Lg变化（1.2～4.8 mH）靠近虚轴的主导极点所对应的根轨迹变化情况。图5中，区域1表示采用直接电网电压前馈控制策略（Kf=1）时的根轨迹；区域2表示采用基于加权系数的电网电压前馈控制策略（以Kf=0.7为例）时的根轨迹。根据图5，区域2的根轨迹与区域1相比更加远离虚轴，表明了采用基于加权系数的电网电压前馈策略可以增加并网逆变器的稳定性。另外，区域2的根轨迹对应的阻尼比高于区域1，因此并网逆变器在输出并网电流指令值动态变化过程中超调量更小。

图5 闭环传递函数根轨迹Fig.5 Root locus of closed loop transfer function

继续增大电网阻抗，原先远离右半平面的实轴非主导极点会逐渐靠近虚轴，从而转变成为了主导极点，此时就会导致系统稳定性的下降，为了对比明显，根据式（6）绘制了电网阻抗由1.2 mH增加到48 mH时，闭环传递函数主导极点和非主导极点的变化情况，如图6所示。其中，虚线椭圆形框表示的是基于加权系数的电网电压前馈控制策略，虚线矩形框表示的是直接电网电压前馈控制策略，箭头方向表示电网阻抗增大时极点的变化方向。由图6可以看出，基于加权系数的电网电压前馈控制策略的极点相比于直接电网电压前馈控制策略更加远离虚轴，即稳定性更好；并且，随着电网阻抗增大，区域1和区域2中表示的主导极点逐渐远离虚轴，而区域3中表示的实轴上非主导极点会逐渐趋于虚轴，即在一定电网阻抗范围内，区域1和区域2中表示的极点为对稳定性起主导作用，此时随着电网阻抗的增大，基于加权系数的电网电压前馈控制策略下的并网逆变器稳定性会有所增加；而当随着电网阻抗继续增大，区域3中表示的极点就会逐渐对稳定性起主导作用，这时系统稳定性会随着电网阻抗的增大而下降。

图6 当电网阻抗大范围变化时闭环传递函数根轨迹Fig.6 Root locus of closed loop transfer function when grid impedance varies widely

2.3 基于阻抗稳定性判据的稳定性分析

文献[9]表明，PCC点存在较大的感抗会导致逆变器-电网系统的阻抗不匹配，进而产生谐波电流。本文通过对基于加权系数的电网电压前馈控制策略的并网逆变器输出阻抗进行建模分析，进一步验证基于前馈滤波的弱网控制策略的有效性。

当电网存在阻抗时，并网逆变器和电网两者可以看成是一个级联系统，其稳定性可以采用文献[9]提出的级联系统阻抗稳定判据来判断。该判据是将并网逆变器表示为诺顿等效电路，即并网逆变器可以视作电流源Ic并联输出阻抗Zo（s），电网则可以看作理想电压源eg串联电网阻抗Zg（s），如图7所示。根据阻抗稳定性判据，系统要稳定必须满足2个条件：①1/Zo（s）稳定；②Zg（s）/Zo（s）满足奈奎斯特（Nyquist）稳定判据。

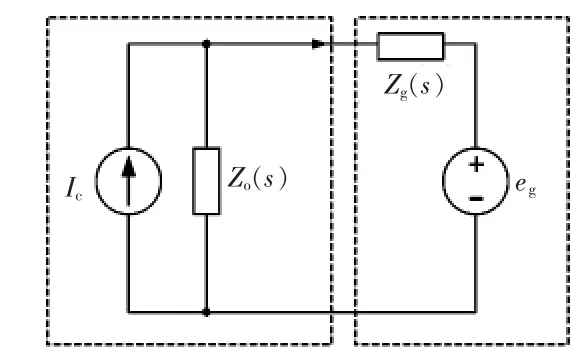
图7 诺顿等效电路Fig.7 Norton equivalent circuit

在弱电网条件下，电网阻抗不能忽略，只要保证并网电流闭环和锁相环稳定，稳定判据条件1就自然满足。 而稳定判据条件 2 要求 Zg（s）/Zo（s）满足奈奎斯特（Nyquist）稳定判据，即要求 Zg（s）/Zo（s）在0 dB处有一定的相位裕度。

设 Zg（s）/Zo（s）为 0 dB 时对应的频率为交截频率ωc，则相位裕度PM为

考虑最恶劣情况，电网阻抗设置为纯电感，则其相位始终为 90°，式（7）可化简为

可见，要保证相位裕度大于0°时闭环稳定，Zo（s）在交截频率 ωc处的相位必须大于-90°。

根据图2，基于加权系数的电网电压前馈控制策略的并网逆变器输出阻抗为

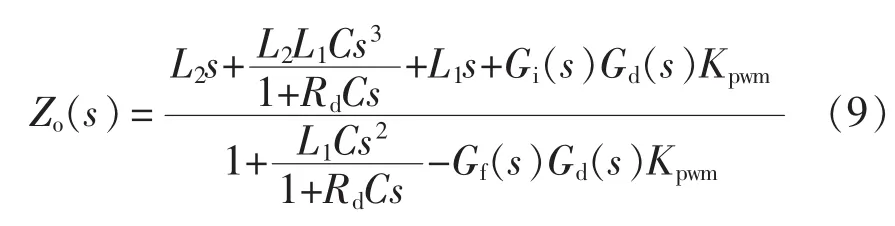
根据表1中的参数，绘制基于加权系数的电网电压前馈控制策略（以Kf=0.6、0.7和0.8为例）和直接电网电压前馈控制策略（Kf=1.0）的输出阻抗Bode图，以及电网阻抗Lg=1.2 mH时的Bode图，如图8（a）所示。 根据图 8（a），随着 Kf的减小，逆变器Zo（s）与电网阻抗 Zg（s）的交截频率 ωc逐渐增大，同时对应的相位裕度也在增大，即采用基于加权系数的电网电压前馈控制能够使Zo（s）在交截频率ωc处的相位大于-90°，因此由阻抗稳定性判据可知，此时并网逆变器的稳定裕度得到了大幅提高，进一步验证了该控制策略的有效性。

根据表1中的参数，绘制基于加权系数的电网电压前馈控制策略（以Kf=0.7为例）在不同电流环PI调节器参数情况下的输出阻抗Bode图，如图8（b）所示。 其中，PI=1.1 p.u.、1 p.u.和 0.9 p.u.分别表示表1中PI调节器参数的1.1倍，1倍和0.9倍。根据图8（b）可见，随着电流环PI参数的增大，并网逆变器与电网阻抗Zg（s）的交截频率ωc基本不变，同时对应的相位裕度也变化很小，即通过增大并网逆变器电流环PI调节器参数的方式，来增加并网逆变器系统的闭环增益，在提高并网逆变器基波跟踪性能的同时，对系统的稳定性的影响很小。

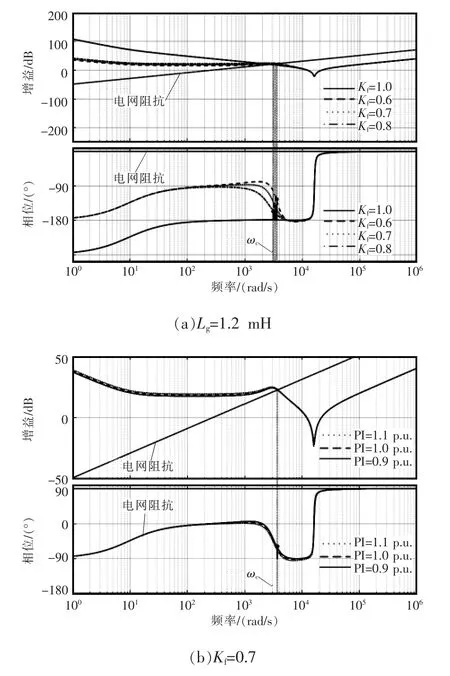
图8 输出阻抗和电网阻抗Bode图Fig.8 Bode plot of output impedance and grid impedance

3 仿真和实验

3.1 仿真验证

为了验证上述理论分析的正确性，利用Matlab/Simulink搭建了三相LCL型并网逆变器的仿真平台，其主要参数与表1相同。

图9给出了当电网阻抗Lg=1.2 mH时，采用直接电网电压前馈控制策略（Kf=1）和基于加权系数的电网电压前馈控制策略（Kf=0.7）的三相输出电流的仿真波形及其THD分析结果。根据图9，采用基于加权系数的电网电压前馈控制策略时输出并网电流的THD为2.30%，小于采用直接电网电压前馈控制策略时的THD值（5.23%），明显抑制了由于电网阻抗导致的输出并网电流的低频谐振，验证了采用基于加权系数的电网电压前馈控制策略的有效性。

图9 输出并网电流仿真波形及其THD分析结果Fig.9 Simulation waveforms of output grid-connected current and its THD analysis results

3.2 实验验证

在实验室搭建了一套20 kW的三相LCL型并网逆变器实验平台，其参数与表1一致。实验平台如图10所示。其中，#1和#2逆变器均为20 kW并网逆变器，二者构成背靠背系统，其中#1逆变器作为直流电源给另外一台供电。并通过人为串入1.2 mH实际电抗器组的方式来模拟电网阻抗。实验平台采用数字信号控制器TMS320F2808实现闭环控制。

图10 并网逆变器实验平台Fig.10 Experimental platform of grid-connected inverter

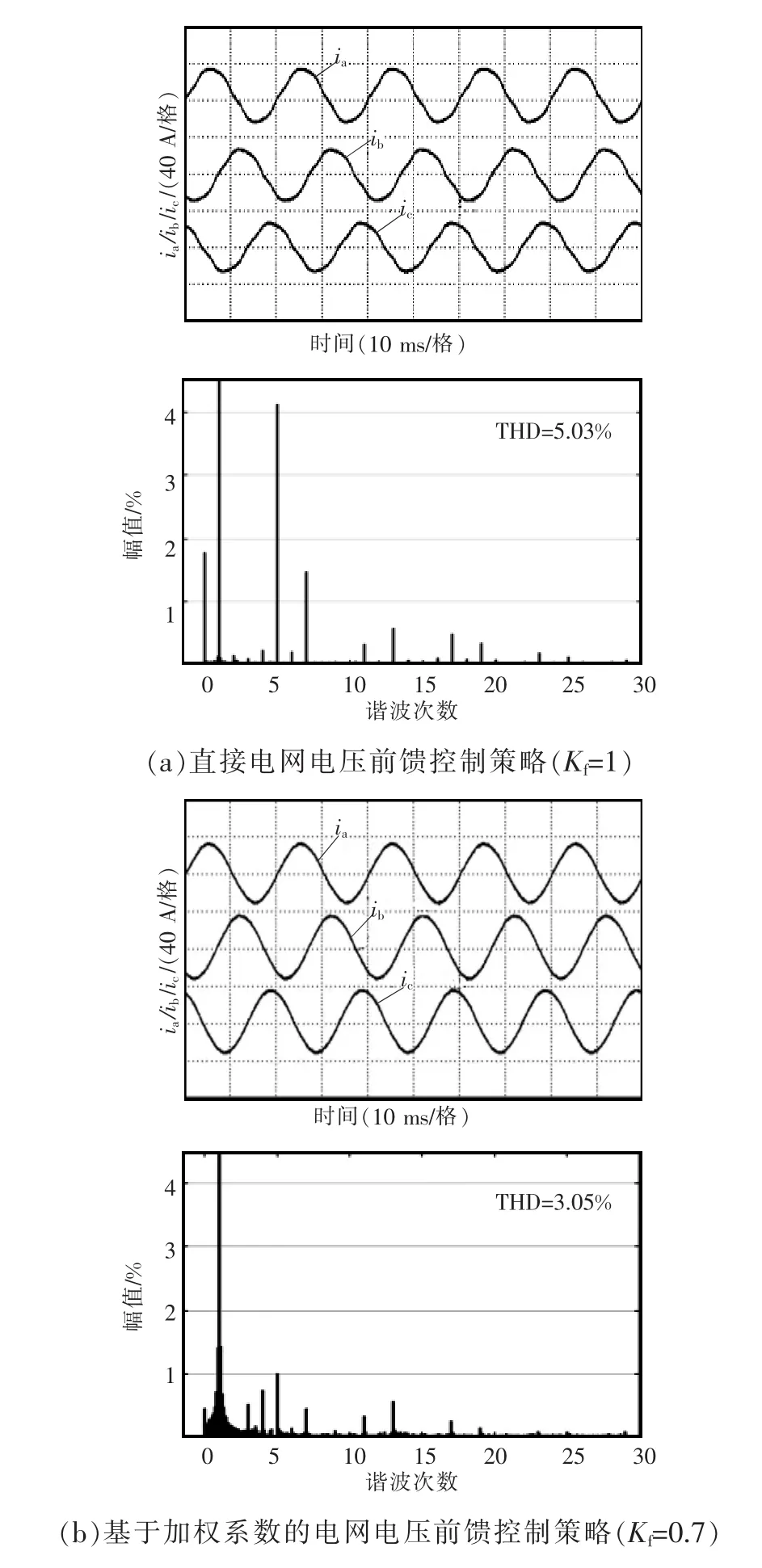
图11 输出并网电流实验波形及其THD分析结果Fig.11 Experimental waveforms of output gridconnected current and its THD analysis results

当电网阻抗Lg=1.2 mH时，图11给出了采用直接电网电压前馈控制策略（Kf=1）和基于加权系数的电网电压前馈控制策略（Kf=0.7）的三相输出电流的实验波形及其THD分析结果。其中，图11（b）和图11（a）相比，前者的PI调节器的比例和积分参数为后者的1.1倍。图12给出了分别在以上两种控制策略下，输出并网电流d轴分量给定值由半载到满载阶跃变化时得到的动态实验波形。

根据图11可见，采用基于加权系数的电网电压前馈控制策略时输出并网电流的THD为3.05%，小于采用直接电网电压前馈控制策略时的5.03%，明显抑制了由于电网阻抗导致的输出并网电流的低频谐振，表明了采用基于加权系数的电网电压前馈控制策略的有效性。 图11（a）和图11（b）输出并网电流的幅值分别为30.1 A和30.2 A，可见通过增大PI调节器的比例和积分参数，可以提高基于加权系数的电网电压前馈控制的基波增益，降低并网逆变器的稳态跟踪误差，验证了第2.1节中的结论。

由图12可知，采用基于加权系数的电网电压前馈控制策略时，由半载到满载切换时的输出并网电流的调节时间为25 ms，大于采用直接电网电压前馈控制时的15 ms，验证了第2.1节中的结论。并且，采用基于加权系数的电网电压前馈控制策略时，由半载到满载切换时的输出并网电流的幅值超调量为4.5 A，要小于采用直接电网电压前馈控制时的8 A超调量，验证了第2.2节中的结论。

图12 输出并网电流d轴分量给定值阶跃变化时的动态实验波形Fig.12 Experimental waveform of output grid-connected current d-axis component by step change of reference value

4 结论

（1）基于加权系数的电网电压前馈控制策略和传统直接电网电压前馈控制相比，前者能够很好地提高并网逆变器在弱电网下的稳定性，并且增大系统的阻尼比，降低输出并网电流指令值动态变化过程中的超调量，但是，同时会增加调节时间，降低其控制带宽和动态性能。

（2）根据阻抗稳定性判据，基于加权系数的电网电压前馈控制策略和传统直接电网电压前馈控制策略相比，其输出阻抗的相位更加远离-90°，其稳定性更好。

（3）通过增大PI调节器的比例和积分参数，可以提高基于加权系数的电网电压前馈控制的基波增益，降低并网逆变器的稳态跟踪误差。

[1]Timbus A,Liserre M,Teodorescu R,et al.Evaluation of current controllers for distributed power generation systems[J].IEEE Transactions on Power Electronics,2009,24（3）:654-664.

[2]Wang Jing,Song Yulun,Monti A.A study of feedforward control on stability of grid-parallel inverter with various grid impedance[C].Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems（PEDG）,2014:1-8.

[3]杨东升,阮新波,吴恒.提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J].中国电机工程学报,2014,34（15）:2327-2335.Yang Dongsheng,Ruan Xinbo,Wu Heng.A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J].Proceedings of the CSEE,2014,34（15）:2327-2335（in Chinese）.

[4]Chen Xin,Zhang Yang,Wang Shanshan,et al.Impedancephased dynamic control method for grid-connected invert-ers in a weak grid[J].IEEE Transactions on Power Electronics,2017,32（1）:274-283.

[5]Xu Jinming,Tang Ting,Xie Shaojun.Research on low-order current harmonics rejections for grid-connected LCL-filtered inverters[J].IET Power Electronics,2014,7（5）:1227-1234.

[6]Chen Xin,Wang Yuncheng,Zhang Yang,et al.Hybrid damping adaptive control scheme for grid-connected inverters in a weak grid[J].IET Power Electronics,2016,9（15）:2760-2768.

[7]李小强,伍小杰,耿乙文,等.感性电网阻抗下三相光伏逆变器稳定性分析[J].中国电机工程学报,2014,34（18）:2906-2916.Li Xiaoqiang,Wu Xiaojie,Geng Yiwen,et al.Stability analysis of three-phase PV inverter under inductive grid impedance condition[J].Proceedings of the CSEE,2014,34（18）:906-2916（in Chinese）.

[8]Liserre M,Teodorescu R,Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Transactions on Power Electronics,2006,21（1）:263-272.

[9]Sun Jian.Impedance-based stability criterion for grid-connected inverters[J].IEEE Transactions on Power Electronics,2011,26（11）:3075-3078.

[10]裴建楠,康宁,李思佳,等.弱电网情况下光伏并网系统的控制策略研究[J].电测与仪表,2015,52（21）:29-33.Pei Jiannan,Kang Ning,Li Sijia,et al.Study on operation control strategy of photovoltaic inverter system connected to weak grid[J].Electrical Measurementamp;Instrumentation,2015,52（21）:29-33（in Chinese）.

[11]严干贵,李龙,黄亚峰,等.弱电网下联网光伏逆变系统稳定性分析及控制参数整定[J].太阳能学报,2013,34（11）:1853-1859.Yan Gangui,Li Long,Huang Yafeng,et al.Stability analysis and control parameters tuning of grid-connected photovoltaic inverter system in weak grid[J].Acta Energiae Solaris Sinica,2013,34（11）:1853-1859（in Chinese）.

[12]许津铭,谢少军,唐婷.弱电网下LCL滤波并网逆变器自适应电流控制[J].中国电机工程学报,2014,34（24）:4031-4039.Xu Jinming,Xie Shaojun,Tang Ting.An adaptive current control for grid-connected LCL-filtered inverters in weak grid case[J].Proceedings of the CSEE,2014,34（24）:4031-4039（in Chinese）.

[13]王学华,阮新波,刘尚伟.抑制电网背景谐波影响的并网逆变器控制策略[J].中国电机工程学报,2011,31（6）:7-14.Wang Xuehua,Ruan Xinbo,Liu Shangwei.Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics in grid voltage[J].Proceedings of the CSEE,2011,31（6）:7-14（in Chinese）.

[14]Cespedes M,Sun Jian.Adaptive control of grid-connected inverters based on online grid impedance measurements[J].IEEE Transactions on Sustainable Energy,2014,5（2）:516-523.

[15]钱强,谢少军,季林,等.一种提升逆变器对电网适应能力的电流控制策略[J].中国电机工程学报,2016,36（22）:6193-6201.Qian Qiang,Xie Shaojun,Ji Lin,et al.A current control strategy to improve the adaptability to utility for inverters[J].Proceedings of the CSEE,2016,36（22）:6193-6201（in Chinese）.

李明

李明（1993-），男，博士研究生，研究方向：新能源利用与分布式发电技术，E-mail：hfmiuu@163.com。

张兴（1963-），男，中国电源学会高级会员，通信作者，教授，博士生导师，研究方向：特种电源、大功率风力发电用变流器及大型光伏并网发电，E-mail：honglf@us tc.edu.cn。

杨莹（1992-），女，硕士研究生，研究方向：电力电子与电力传动，E-mail：10143 34465@qq.com。

赵文广（1988-），男，博士研究生，研究方向：新能源利用与分布式发电技术，E-mail：643370597@qq.com。

Grid Voltage Feedforward Control Strategy Based on Weighting Coefficient in Weak Grid

LI Ming,ZHANG Xing,YANG Ying,ZHAO Wenguang
（School of Electrical Engineering and Automation,Hefei University of Technology,Hefei 230009,China）

Control performance of grid-connected inverter are affected by the grid voltage background harmonics and variable grid impedance.Due to its ease of implement ation and effective suppression of background harmonics,the direct voltage proportional feedforward

wide attention.However,this control strategy will reduce the phase margin of the current control and effect grid stability in weak grid.The grid voltage feedforward control strategy based on the weighted coefficient can significantly improve the stability of grid connected inverters despite the reduction of the fundamental wave gain.Firstly,combined with the impedance stability criterion,to analyse and compare the dynamic and static performance of the grid voltage feedforward control strategy based on weighting coefficient and the traditional direct voltage feedforward control strategy.It is concluded that the proposed strategy has better adaptability to the grid in weak grid.Secondly,the theoretical analysis of improving the fundamental tracking performance of grid connected inverters is given by adjusting the closed-loop gain of the system.Finally,Matlab/Simulink simulation and experiments are carried out to further verify the effectiveness of the grid voltage feed-forward control strategy based on the weighted coefficient in the weak grid.

grid-connected inverter;grid impedance;weak grid;grid voltage feedforward;weighting coefficient

10.13234/j.issn.2095-2805.2017.6.10

TM464

A

2017-05-30；

2017-09-24

国家重点研发计划资助项目（2016YFB0900300）；国家自然科学基金资助项目（51677049）

Project Supported by National Key Ramp;D Program of China（201 6YFB090030 0）;National Natural Science Foundation of China（51677049）