多因素诱发海底管道轴向定向位移量计算方法

彭碧瑶，刘 润，王秀妍，李成凤

(天津大学 水利工程仿真与安全国家重点试验室，天津 300072)

多因素诱发海底管道轴向定向位移量计算方法

彭碧瑶，刘 润，王秀妍，李成凤

(天津大学 水利工程仿真与安全国家重点试验室，天津 300072)

深水管道的启闭作业造成了管道内部温度与压力的往复施加，导致管道产生沿轴向的定向位移(“walking”现象)，成为油气输送系统安全的重大隐患，准确预测管道的轴向定向位移量是提出防控措施的关键。首先阐明当管道受到来自悬链线立管(SCR)张力、海床倾角以及内部瞬态热梯度作用时产生轴向定向位移的机理；建立单因素与多因素诱发管道轴向定向位移的数值模拟方法，揭示管道轴向定向位移量与不同诱因之间的非线性对应关系；修正单因素诱发管道轴向定向位移量的计算公式，提出了多因素耦合作用下确定管道轴向定向位移量的方法。

海底管道；轴向定向位移；瞬态热梯度；立管张力；海床倾角

为满足水下生产系统的工艺要求，海底油气管道在工作过程中常被施加高温高压以保证输送介质的流动性。自1981年至2003年，海底油气管道的设计承温能力由120℃增加至170℃[1]，随着这种趋势不断增长，由高温高压的操作环境而引起的海底管道轴向定向位移现象也逐渐被工程研究人员所重视。海底管道的轴向定向位移本身并不会导致管道的失效，但有可能造成与其连接的三通/四通或跨接管道出现过应力；SCR丧失张力；管道水平屈曲处应力过大等不良影响[2]，严重危害水下生产系统的使用安全。

对于这一问题诸多学者进行了相关分析研究，1997-1998年，NystrØm[3]、Konuk[4]曾对此类现象进行过描述，直到2000年，挪威学者Tornes等[5]结合阿美拉达斯赫(Amerada Hess)公司英国分部在北海油田所得的监测数据，首次提出了管道的“轴向爬行”现象，并依据出现该现象的特征将管道进行了“长短”分类。此后，Bruton等[1]在2003年正式将管道产生轴向整体位移的现象命名为管道的轴向“walking”，并提出“短管”一端所连接的SCR提供的张力，也会引起管道向有张力的一端发生轴向定向位移。2007年，Lagos大学Olunloyo等[6]考虑了管内流体的横向和轴向振动对轴向定向位移的影响，建立了非线性方程并对其求解，证实其对轴向定向位移的影响并不大。2008年，Carr等[2]系统地对管道的轴向定向位移成因进行了分析，发现除瞬态热梯度和SCR所提供的张力可引发管道定向位移外，海床沿管道的轴向方向存在坡度也会使得管道产生向下坡方向的轴向位移，并在此基础上提出了一种估算管道轴向定向位移量的解析方法。2009年，澳大利亚学者Cumming[7]运用有限元方法进一步分析了不同形式的海床、约束对管道轴向定向位移的影响，并对管道的水平屈曲和轴向位移之间的相互作用进行了分析。同年，Rong[8]通过数值方法建立了海床坡度和瞬态热梯度耦合作用下的管道轴向定向位移模型，并对摩擦系数和轴向抗力曲线的弹性段所对应的位移进行了敏感度分析，发现摩擦系数减小到一定程度时，海床坡度引发的管道轴向定向位移距离剧增，而瞬态热梯度所引发的管道轴向定向位移量则会减小。2010年，Carr[9]首次提到由于停输后的气液分离现象，并且发现置于斜坡上的多相流管道也会导致管道发生轴向定向位移，同时对该情况下的轴向定向位移的大小进行了解析分析和有限元验证。此后，新加坡学者Chen[10]研究了管中管系统的轴向位移机理，运用有限元方法分析了垫片与管道之间的摩擦系数、管—土之间的摩擦系数以及瞬态热梯度对walking的影响，并与单层管结果进行了比对，发现管中管系统每个启闭循环的轴向定向位移大小均不相同，而第二个循环后产生的轴向定向位移最大，此后每个循环轴向定向位移逐渐减小。2013年，Liu等[11]运用小比尺试验及数值方法分析了渤海湾软黏土中管道外径、埋深对其受到的轴向约束力的影响规律。同年，Castelo等[12]为了消除管道的轴向定向位移对其进行了锚固，并运用有限元分别分析了在管道高温端、低温端、中点处锚固所需的力的大小，得到中点处所需锚固力较小的结论，并提出了一种减小轴向定向位移的装置。以上研究表明，管道的长度、瞬态温度热梯度及管—土轴向抗力模型对高温高压输送管道的轴向定向位移现象存在较大影响。

现有研究较多关注单一诱因情况下管道轴向定向位移量的计算方法和不同诱因影响程度的分析，而海底管道的工作环境较为复杂，多因素耦合诱发管道轴向定向位移的情况极为常见，目前对于多个因素耦合引发管道轴向定向位移的研究较少，其与单个诱因产生的轴向定向位移之间的联系仍需要进一步讨论，且尚未有学者提出多因素诱发管道轴向定向位移量的计算方法。

下面首先阐述了海底管道在温度往复施加的过程中发生轴向定向位移的运动机理，建立了单因素诱发管道轴向定向位移的数值模型，通过计算结果对已有的单因素诱发管道轴向定向位移的解析算法进行了改进；运用多元非线性回归分析了多因素诱发管道的轴向定向位移规律，提出了多因素耦合作用下管道轴向定向位移量的计算方法。

1 管道轴向位移的发生机理

1.1管道的约束状态

管道的轴向位移规律与其轴向约束状态有着必然联系，根据不同的约束状态，可将管道分为三类：“短管”、“中管”和“长管”。

1.1.1 “短管”的约束状态

如图1所示，升温过程中，管道的轴力会通过轴向运动被释放，由于海床对管道轴向运动的阻碍作用而未能释放的轴向力，即为升温后管道的真实轴力。此后的降温过程中，降温全约束有效轴力同样会通过管道的轴向运动释放掉一部分，降温后管道真实轴力即为因海床对管道运动的阻碍而不能释放的轴力。图中管道有效轴向力的极值点即为管道的虚拟锚固点，且除管道中间的虚拟锚固点(A、B)外，管道上的任意位置在升温降温过程中均可沿轴向自由移动。运动方向如图1 中箭头所示，升温时，管道以A为对称点，向两端膨胀；降温时，以B为对称点(此时A、B重合)，由两端向B点收缩。

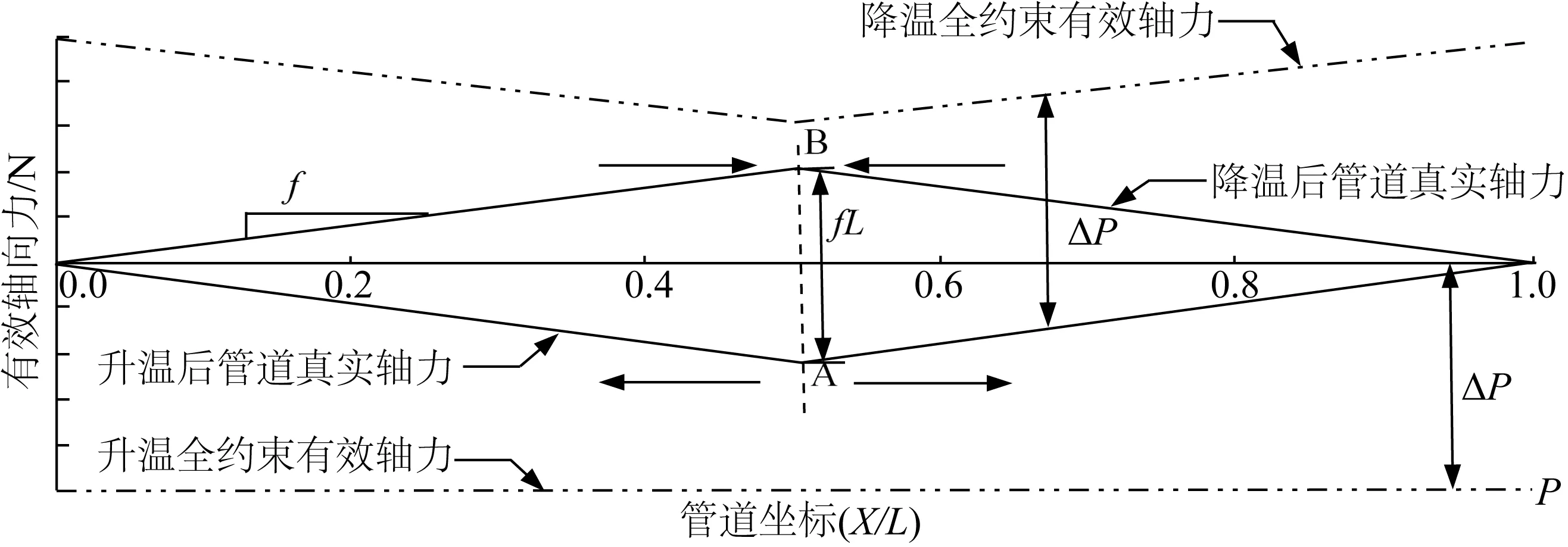
图1 “短管”有效轴向力曲线Fig. 1 Effective axial force profile of “short pipeline”

1.1.2 “中管”的约束状态

图2为1lt;f/f*≤2的管道在升温降温过程中的有效轴力曲线。

图2 “中管”有效轴向力曲线Fig. 2 Effective axial force profile of “middle pipeline”

由图2可知，管道在升温过程中可以克服海床的约束力向两端膨胀(除虚拟锚固点A)，但在降温过程中海床所能提供的轴向约束力使得管道中部的CBD段不能发生轴向位移，仅两端的管道可向中部收缩，于是称其为“中管”。

1.1.3 “长管”的约束状态

当管道的长度足以被海床提供的土抗力完全约束时，称其为“长管”，此时f/f*gt;2，管道在升温降温过程中轴力变化如图3所示。

图3 “长管”有效轴向力曲线Fig. 3 Effective axial force profile of “long pipeline”

由图3可知，管道升温、降温过程中，其中间段的有效轴力均无法克服海床提供的轴向约束力，降温过程锚固段长于升温过程锚固段，于是将其称为管道的完全约束状态。

显然，管道升温、降温过程中所产生的轴力是否可以克服管道所受到的土抗力是管道能否发生轴向位移的关键。由上述分析可知，土抗力系数越大、管道越长，则管道越容易被完全约束，与“长管”相比，“短管”更易发生轴向定向位移。

1.2管道轴向定向位移的发生条件

1.2.1 SCR张力作用

管道均匀升温、降温过程中，假若其一端受到SCR张力作用，则有效轴向力曲线不再对称，如图4所示。

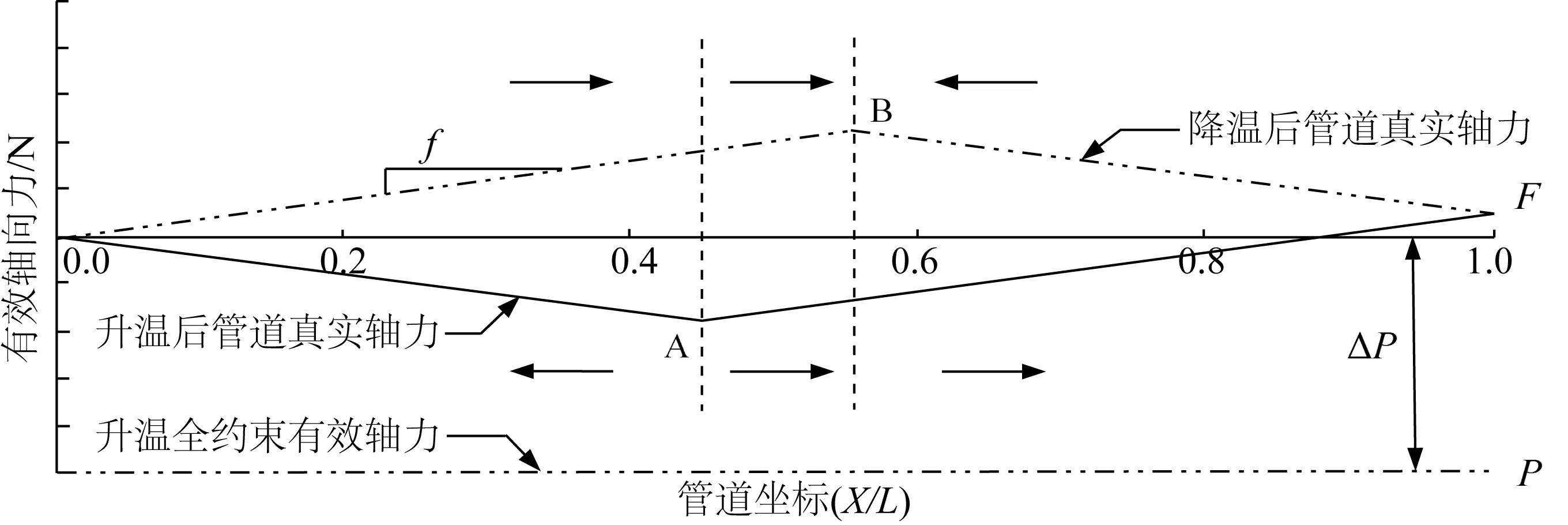
图4 一端受SCR张力作用下管道的有效轴向力曲线Fig. 4 Effective axial force profile of pipeline during SCR at one end

升温过程的虚拟锚固点A和降温过程的虚拟锚固点B不重合，锚固点两侧的管道移动方向如图4中箭头所示，两虚拟锚固点之间(AB段)的管道移动方向均指向张力F一端，可见，管道整体向SCR方向发生轴向位移。

1.2.2 海床倾角作用

图5为管道置于沿管道长度方向倾斜的海床上时，管道加载、卸载状态下的有效轴向力曲线。

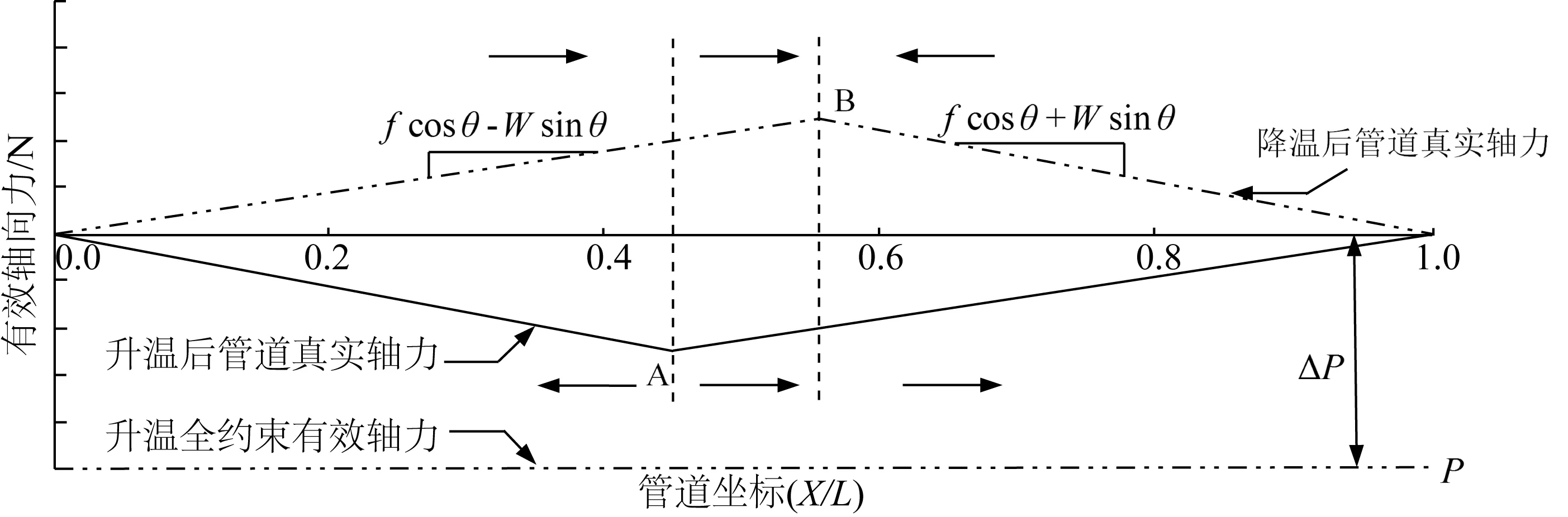
图5 置于倾斜海床上的管道有效轴向力曲线Fig. 5 Effective axial force profile of pipeline laying on the sloping seabed

管道沿斜坡的重力分量与管土间摩擦力的联合作用导致了管道有效轴向力曲线不对称。升温过程的虚拟锚固点A和降温过程的虚拟锚固点B不重合，锚固点两侧的管道移动方向如图5中箭头所示，在虚拟锚固点之间(AB段)的管道移动方向均指向海床较低的一端，管道整体向下坡方向发生位移。

1.2.3 瞬态热梯度作用

管道内的热流流向是评估其轴向定向位移的重要因素。通常将“热流入口”定义为管道的“热端”，将“热流出口”定义为管道的“冷端”。管道开启时，热流由管道的热端向冷端移动，此过程中管道逐渐被加热，其温度曲线如图6所示。

图6 升温过程中管道沿程温度曲线Fig. 6 Temperature profile of pipeline during heating

以经历15步后可整体达到设计温度的管道为例，第9步后管道的出口一端逐渐被加热，由于管道和周围环境存在热交换，管道的温度变化是非线性的。研究表明[2]，管道冷端被加热前的升温过程(图6中1～9步)对于管道的轴向定向位移影响最大，图7给出了管道启闭循环内有效轴力曲线变化。

图7 瞬态热梯度作用下管道有效轴向力曲线Fig. 7 Effective axial force profile during thermal transient

图7(a)为第一个启闭循环内管道的轴力曲线。随着管道逐渐升温，管道的轴力也慢慢被激发，其虚拟锚固点由热端逐渐向管道中点移动，当虚拟锚固点运动到中点A9后，继续升温(图6中9～15步)也不再导致管道轴力发生变化。而降温过程中，管道自然冷却，温度整体均匀变化，当管道温度与外部环境温度一致时，由于土抗力的作用，其内部存在残余的轴力，导致此后的循环中，管道内部轴力演变为图7(b)所示，加剧了管道的轴向定向位移。由此可见，瞬态热梯度诱发的管道轴向定向位移量主要由第二个及之后的工作循环导致。

2 单因素诱发的管道轴向定向位移量分析

单因素诱发管道轴向定向位移是指上述任意一种条件单独存在时，管道产生轴向定向位移的情况。

2.1管道轴向定向位移量解析解

2008年，Carr[2]提出了计算单因素诱发的管道轴向定向位移量的解析解。

SCR张力诱发的每循环管道轴向定向位移量：

海床倾角诱发的每循环管道轴向定向位移量：

瞬态热梯度诱发的每循环管道轴向定向位移量：

式中：F为SCR张力；θ为海床倾斜角度；fq=EAαq，q为管道升温时的瞬态热梯度；其他同上。

2.2管道轴向定向位移的数值解

针对三种单因素诱发的管道轴向定向位移情况分别建立了数值模型，并将计算结果与解析解进行了对比。

2.2.1 数值分析模型

建立ABAQUS数值模型，采用了动力显示算法，土体选用摩尔—库仑本构模型，管道和土体的单元类型分别为PIPE31和C3D8R。对分析步长进行分析后，发现计算步长超过20 s后，计算结果趋于稳定，为减小时间成本，将分析步长定为20 s。将管—土摩擦系数范围确定0.3～0.9之间，管土间接触采用罚接触，管道最高加热至150°C。具体参数如表1和表2所示。管道发生轴向位移时，对周围土体的影响范围较小[13]，因此可忽略计算时的边界效应，为保证管道发生轴向定向位移后仍与土体接触，取土体长度略大于管道长度。

表1 管道参数Tab. 1 Parameters of pipeline

表2 土体参数Tab. 2 Parameters of soil

为体现不同瞬态热梯度对管道轴向定向位移量的影响，将温度简化为线性递减的曲线，分别计算了管道以40 °C/km、50 °C/km和60 °C/km降温的情况，温度曲线如图8所示。

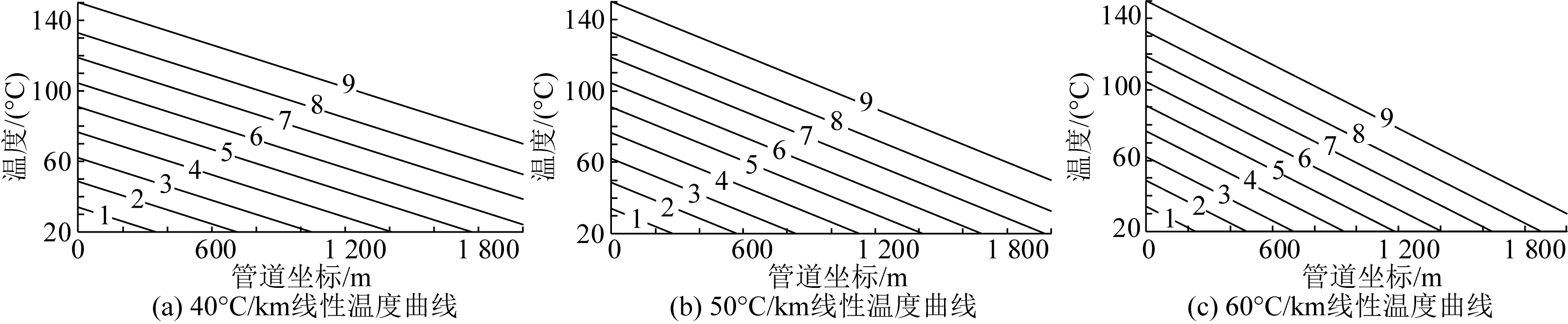
图8 线性温度曲线Fig. 8 Liner temperature profile

2.2.2 数值解与解析解的对比

如图9所示，为验证数值方法的可靠性，选取了SCR张力100～600 kN、海床倾角1°～5°、瞬态热梯度40～60 °C/km的情况进行模拟，观察管道经历了5个升温降温循环后，中点处的轴向位移变化，并对2～5循环内管道中点的轴向定向位移取平均值得到每循环管道中点的轴向定向位移量，与解析解进行对比。

图9 单因素诱发的平均每循环管道中点轴向定向位移量Fig. 9 Single factor induced average axial directional displacement of midpoint on pipeline per cycle

可以看出，由于管—土间摩擦系数不同，平均每循环内管道中点的轴向定向位移在10-2～101m范围内变化，且每循环管道中点的轴向定向位移量随着SCR张力、海床倾角和瞬态热梯度的增大而增大。图9(a)、图9(b)的数值模拟的结果和解析法解具有较好的一致性。图9(c)中，当摩擦系数较大时，解析解所得的结果偏小甚至出现负值，Carr[2]在提出公式时，也指出了这一缺陷，因此，这里对式(3)进行了修正：

图10对比了相同SCR张力或海床倾角作用下，管—土间摩擦系数变化对管道有效轴向力的影响，以F=100 kN和θ=1°为例，给出了管道升到最高温度和降温至环境温度时的有效轴向力曲线。

图10 不同管-土间摩擦系数下管道有效轴向力变化规律Fig. 10 Effective axial force profile under different friction coefficients between pipeline and soil

由图10可知，随着管—土间摩擦系数的增加，管道内累积的有效轴向力也逐渐增大，同时升温—降温循环内管道上产生的虚拟锚固点逐渐向管道中点靠近，两虚拟锚固点之间的距离逐渐缩短。

3 多因素诱发的管道轴向定向位移量分析

在复杂的海洋环境中，上述诱因存在共同发生的情况，因此给出了5种多因素诱发管道轴向定向位移的具体情况，以适用于管道各种复杂的工况，并建立经验公式，得到其与单因素诱发的管道轴向定向位移量的联系。

3.1海床倾角与SCR张力耦合

如图11所示，海床倾角与SCR张力共同作用诱发管道定向位移的情况可分为顺向耦合和逆向耦合两种。顺向耦合指SCR张力指向下坡方向，逆向耦合指其张力指向上坡方向。

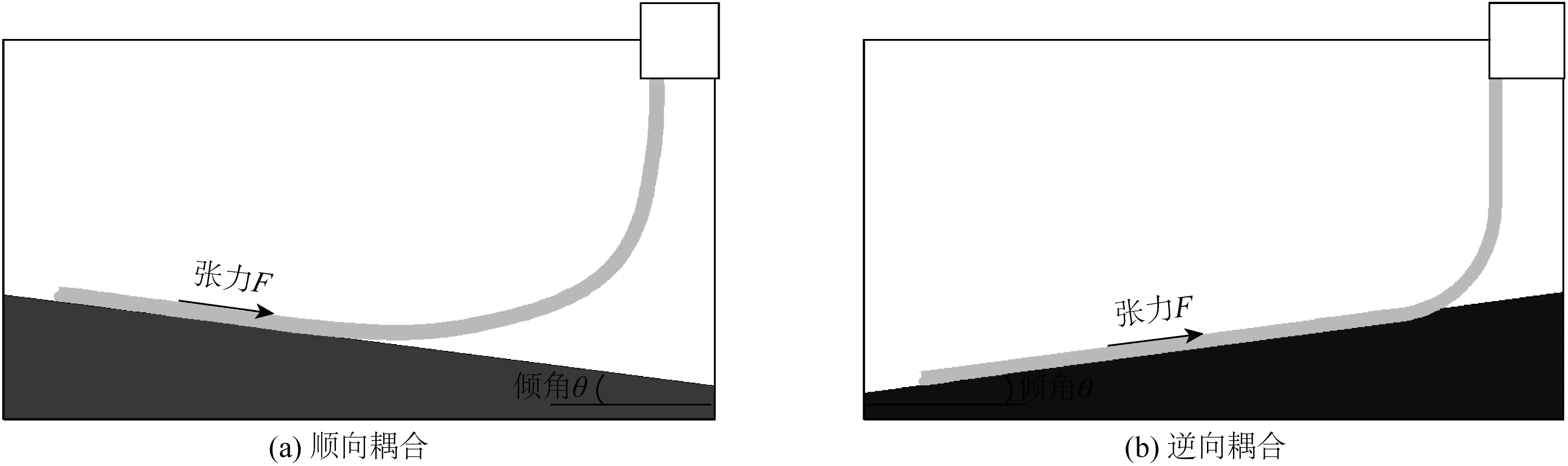
图11 倾角θ与张力F耦合示意Fig. 11 Angle θ coupling with tension F

在分析倾角θ和张力F发生顺、逆向耦合作用下管道轴向定向位移时，选取1°～5°的海床倾角和100～400 kN的SCR张力，研究了不同倾角角度和张力大小对管道中点处每循环轴向定向位移量的影响，对2～5循环内管道中点处的轴向定向位移量取平均值，如图12所示。

图12 θ-F顺、逆向耦合时平均每循环管道中点轴向定向位移量Fig. 12 Average axial directional displacement of midpoint on pipeline per cycle caused by θ coupling with F

管道中点的轴向定向位移量随着张力或海床倾角的增加呈线性增长，且不论是顺向耦合还是逆向耦合，平均每循环管道中点的轴向定向位移量与立管张力和海床倾角各自单独诱发的管道中点轴向定向位移量线性相关，即：

式中：Xθ±F为海床倾角与张力耦合时平均每循环管道中点的轴向定向位移量；Xθ，XF可由式(1)、(2)求得；“±”与耦合方式有关，顺向耦合时取“+”号，逆向耦合时取“-”号。

3.2瞬态热梯度与海床倾角耦合

瞬态热梯度与海床倾角的耦合同样存在顺向与逆向两种方式。如图13所示，管道热端位于海床上坡处时，瞬态热梯度和海床倾角所引起的管道轴向位移均朝向下坡方向，这种情况被称为这两种诱因的顺向耦合；反之，当管道冷端位于上坡处时，瞬态热梯度和海床倾角所引起的管道轴向位移方向相反，则称之为逆向耦合。

图13 瞬态热梯度q与海床倾角θ度耦合Fig. 13 Thermal gradient q coupling with angle θ

图14给出了q-θ耦合时，平均每循环管道中点的轴向定向位移量的数值解与q、θ分别诱发管道轴向定向位移量解析解之和的对比情况。

图14 q-θ耦合时平均每循环管道中点轴向定向位移量Fig. 14 Average axial directional displacement of midpoint on pipeline per cycle caused by q coupling with θ

观察可知，q-θ耦合时，不论是顺向耦合还是逆向耦合，管道每循环轴向定向位移量的绝对值均小于这两种因素单独诱发的管道轴向定向位移量之和的绝对值。且耦合情况下，管道每循环的轴向定向位移量的绝对值随着瞬态热度梯度q的增大而减小，随着海床倾角θ的增大而增大。为得到q-θ耦合情况下，管道每循环轴向定向位移量及方向，运用MATLAB对大量数值结果进行多元非线性回归分析，提出了如下的经验公式：

式中：Xq±θ为瞬态热梯度与海床倾角耦合时，平均每循环管道中点的轴向定向位移；Xq可通过式(3)求得；“±”与耦合方式有关，顺向耦合时取“+”号，逆向耦合时取“-”号。参数a、b、c与管—土间摩擦系数有关，并可根据不同耦合方式查图15得到。

图15 q-θ耦合时参数值曲线Fig. 15 Parameters profile of q-θ coupling

3.3瞬态热梯度与SCR张力耦合

实际工程中，管道与SCR相连的一侧通常为冷端，因此瞬态热梯度与SCR张力共同诱发轴向定向位移时，只需分析一种情况，如图16所示。

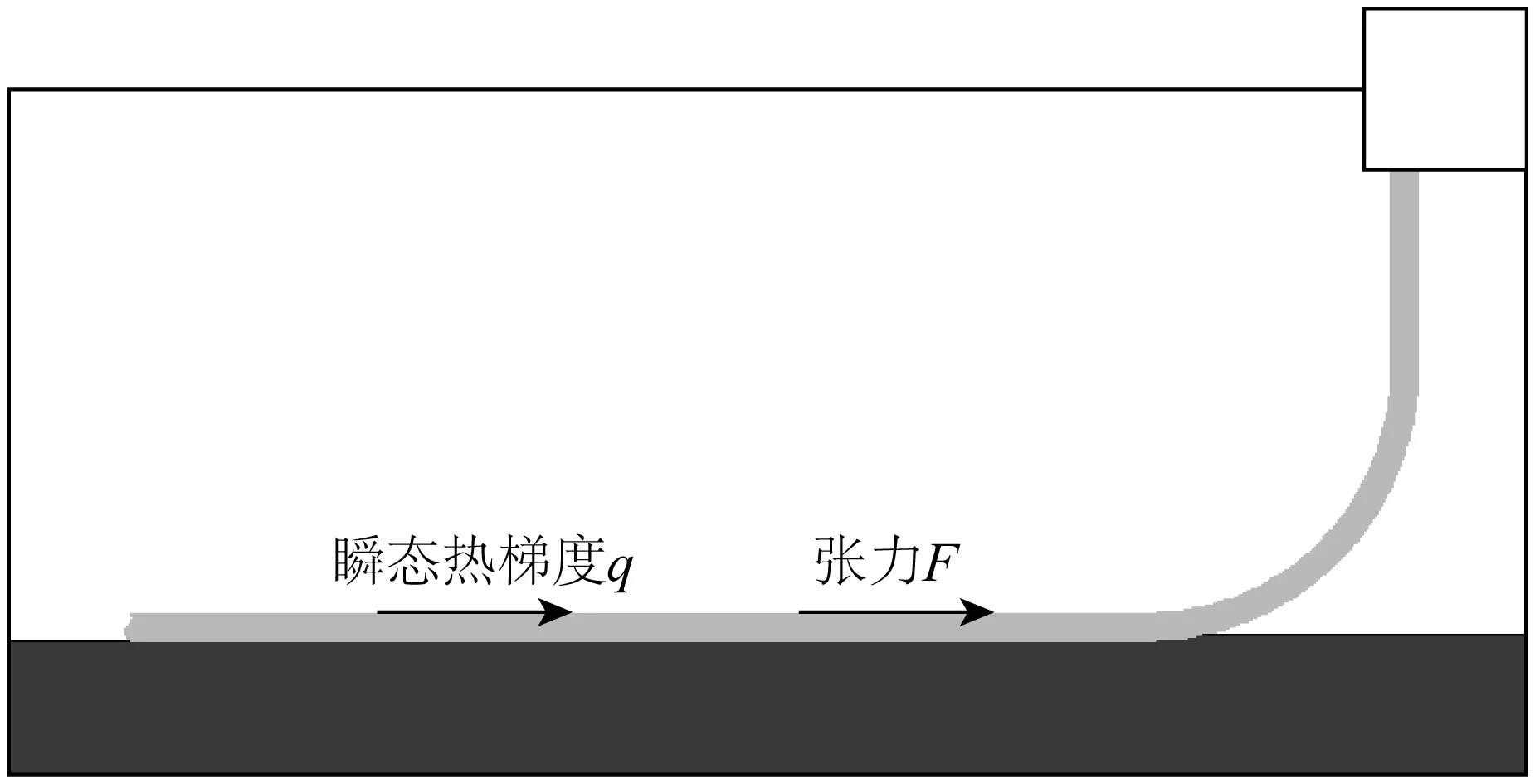
图16 瞬态热梯度q与立管张力F耦合Fig. 16 Thermal gradient q coupling with tension F

图17给出了q-F耦合时，不同热梯度幅值和张力大小共同作用所诱发的管道轴向定向位移量的变化规律 。

图17 q-F耦合时平均每循环管道中点轴向定向位移量Fig. 17 Average axial directional displacement of midpoint on pipeline per cycle caused by q coupling with F

耦合时，平均每循环管道发生的轴向定向位移量小于q和F各自单独诱发的管道轴向定向位移之和，且管道的轴向定向位移量随着瞬态热梯度q的增大而减小，随着张力F的增大而增大。同样，为得到q-F耦合时平均每循环管道的轴向定向位移量，依据大量数值分析结果，提出了如下的经验公式：

式中：Xq+F为瞬态热梯度与SCR张力耦合时，平均每循环管道的轴向定向位移；参数a、b、c与摩擦系数有关，并可由图18查得。

图18 q-F耦合时参数值曲线图Fig. 18 Parameters profile of q-F coupling

4 结 语

阐述了管道发生轴向定向移动的力学机制，在验证数值分析方法正确性的基础上，通过大量数值模拟研究了单因素和多因素诱发的管道轴向定向位移现象，得到如下结论：

1)单因素诱发的管道轴向定向位移量随着SCR张力、海床倾角和瞬态热梯度的增大而增大。

2)管-土间摩擦系数对管道轴向位移影响显著，当管土间摩擦系数增加时，SCR张力与海床倾角诱发的管道轴向定向位移量非线性减小，由瞬态热梯度诱发的管道轴向定向位移量呈先增大后减小趋势。

4)开展了多因素诱发管道轴向定向位移的数值模拟。揭示了多因素与单因素诱发管道轴向定向位移的关联，针对外径为12英寸的短管，提出了双因素耦合诱发管道轴向定向位移量的计算方法，以图表方式给出了公式中经验系数的取值。

[1] BRUTON D, CARR M, LESLIE D. Lateral buckling and pipeline walking, a challenge for hot pipelines[C]//Proceedings of the Offshore Pipeline Technology Conference. 2003.

[2] CARR M, SINCLAIR F, BRUTON D. Pipeline walking-understanding the field layout challenges, and analytical solutions developed for the SAFEBUCK JIP[J]. Spe Projects Facilities amp; Construction, 2008, 3(3):1-9.

[3] NYSTRØM P R. 3-D dynamic buckling and cyclic behaviour of HP/HT flowlines[C]//Proceedings of the Seventh International Offshore and Polar Engineering Conference. Honolulu: ISOPE, 1997：299-307.

[4] KONUK I. Expansion of pipelines under cyclic operational conditions: Formulation of problem and development of solution algorithm[C]//Proceedings of the 17th International Conference on Offshore Mechanics and Arctic Engineering. 1998: 1103.

[5] TORNES K, JURY J, OSE B A, et al. Axial creeping of high temperature flowlines caused by soil ratcheting[C]//Proceedings of the Conference on Offshore Mechanics and Arctic Engineering. New Orleans: ASME, 2000: 1229-1239.

[6] OLUNLOYO V O S, OYEDIRAN A A, ADEWALE A, et al. Concerning the transverse and longitudinal vibrations of a fluid conveying beam and the pipe[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. San Deigo: ASME, 2007: 29304.

[7] CUMMING G, DRUZYNSKI A, TORNES K, et al. Lateral walking and feed-in of buckled pipelines due to interactions of seabed features[C]//Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering. Honolulu: ASME, 2009: 79901.

[8] RONG H, INGLIS R, BELL G, et al. Evaluation and mitigation of axial walking with a focus on deep water flowlines[C]//Proceedings of the Offshore Technology Conference. Houston: OTC, 2009: 19862.

[9] BRUTON D A S, SINCLAIR F, CARR M. Lessons learned from observing walking of pipelines with lateral buckles, including new driving mechanisms and updated analysis models[C]//Proceedings of the Offshore Technology Conference. Houston: OTC, 2010: 20750.

[10] CHEN Q, CHIA H K. Pipe-in-pipe walking: Understanding the mechanism, evaluating and mitigating the phenomenon[C]//Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering. China: ASME, 2010: 20058.

[11] LIU R, BASU P, XIONG H. Laboratory tests and thermal buckling analysis for pipes buried in Bohai soft clay[J]. Marine Structures, 2015, 43:44-60.

[12] CASTELO A, TARDELLI L, GALGOUL N S, et al. Anchoring strategy suggested for the mitigation of pipeline walking [C]//Proceedings of the International Conference on Ocean, Offshore and Arctic Engineering. Nantes: ASME, 2013: 10070.

[13] 王洪播. 海底管线水平向屈曲过程中管土相互作用研究[D].天津: 天津大学, 2010. (WANG H B. Study on the interaction between soil and submarine pipeline in lateral buckling mode[D]. Tianjin: Tianjin University, 2010. (in Chinese))

Calculation method of multi-factor induced axial directional displacement of submarine pipelines

PENG Biyao, LIU Run, WANG Xiuyan, LI Chengfeng

(State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)

An overall axial directional displacement is found in submarine pipelines, caused by their circular high pressure and high temperature. This phenomenon is called “pipeline walking”, threatening the underwater production safety. In order to prevent and control the pipeline walking, it is important to predict axial directional displacement accurately. This paper discusses the mechanism of three single factors leading to the flowlines axial directional movement, which are steel catenary riser (SCR) tension, sloping seabed and thermal transient. Numerical models of both single factor and multi-factor induced axial directional movement were established, aiming to analyze the nonlinear relationship between the inducements and the axial directional displacement of flowlines. The existing formula of single factor induced axial directional displacement of pipelines was revised and a new calculation method of multi-factor induced axial directional displacement in submarine pipelines was developed.

submarine pipelines; axial directional displacement; thermal transient; SCR tension; sloping seabed

1005-9865(2017)06-0084-10

P756.2；TE58

A

10.16483/j.issn.1005-9865.2017.06.010

2017-03-20

国家重点基础研究发展计划(973计划)项目(2014CB046802)；国家自然科学基金(51679162)

彭碧瑶(1993-)，女，天津人，硕士研究生，主要从事结构物与土的相互作用研究。E-mail: maggie_peng@tju.edu.cn