半刚性组合框架骨架曲线实用计算方法

潘建荣，杨正挺，王湛，陈士哲

半刚性组合框架骨架曲线实用计算方法

潘建荣1,2，杨正挺1，王湛1,2，陈士哲1

(1. 华南理工大学 土木与交通学院，广东 广州，510640；2. 华南理工大学 亚热带建筑科学国家重点实验室，广东 广州，510640)

针对组合节点的弯矩−转角计算模型以及组合框架骨架曲线计算模型忽略节点半刚性的问题，探讨组合节点转动刚度和半刚性组合框架骨架曲线的计算方法。基于参数相关性，运用改进的参数灵敏度分析方法，研究外加强环式钢管混凝土柱−钢梁节点的转动刚度。应用二阶分析推导柔性梁柱单元的刚度矩阵；应用得出的节点转动刚度计算模型推导半刚性组合框架骨架曲线的简化计算模型。研究结果表明：改进后的灵敏度分析方法得出的节点参数灵敏度更高。节点半刚性可降低骨架曲线的弹性刚度和下降段斜率。引入节点半刚性的骨架曲线计算模型更加符合组合框架的实际工作性能。

半刚性；灵敏度分析；弯矩−转角曲线；组合框架；骨架曲线计算模型

钢管混凝土结构体系由于具有承载力高、施工方便和节约材料等特点，近年来在工程中得到越来越广泛的应用。其中，组合结构节点的转动刚度和组合框架的抗震性能一直是工程界关注的重点[1]。众所周知，梁柱连接节点的半刚性对框架力学性能的影响不容忽视。外加强环式钢管混凝土柱−钢梁节点是最常见的组合节点形式之一，是一种半刚性节点。陈鹃等[2−4]以节点刚性试验及有限元分析证明了这一结论。传统的节点半刚性计算模型大多是通过单一变化参数进行参数拟合而得到的，模型中的参数很少具有明确的物理意义。而且在进行参数化分析时，大多是基于节点设计变量完全确定的假设(单独变化其中1个参数，固定其他参数)，忽略了各设计变量间的相关关系，因而不能准确分析设计变量对节点半刚性的影响方式和影响程度。恢复力模型是进行结构抗震分析的前提。在进行理论推导时，恢复力模型可通过骨架曲线计算模型扩展得到，因此，得出恢复力模型的关键是得出其骨架曲线计算模型。单层单跨结构是框架结构的最基本的组成部分，任何框架都可以由其组合变换而来，所以有必要对其恢复力模型进行研究。目前主要针对构件层次即组合梁、组合柱和组合节点进行研究，而对于组合框架的恢复力模型则研究较少。孙修礼等[5]应用IDARC程序进行钢管混凝土柱−钢梁框架的恢复力曲线的研究，验证了轴压比、钢材强度、柱截面含钢率对骨架曲线的影响。戚菁菁等[6]进行了 8榀钢管混凝土组合框架的水平低周往复荷载试验，主要考虑梁柱线刚度比、长细比和柱轴压比对组合框架骨架曲线的影响，并根据试验数据拟合得到了骨架曲线的模型。刘如月等[7]进行了防屈曲偏心支撑混凝土框架试验，并且在试验的基础上进行理论分析得到了框架的恢复力模型。张向冈等[8]进行了 2榀圆钢管再生混凝土柱−钢筋再生混凝土梁框架试验，采用位移幅值承载力突降的特殊处理方法得出特征点，最终得到框架的恢复力模型。王琨等[9]进行了 2榀型钢混凝土梁−角钢混凝土柱组合框架的低周反复荷载试验，并对试验进行数值模拟，基于参数分析得出了该框架的荷载−位移恢复力模型。王先铁等[10]进行了 3榀钢管混凝土柱−钢梁平面框架的拟静力试验，分析了梁柱线刚度比和轴压比对框架抗震性能的影响，提出了框架简化恢复力计算模型。王文达等[11]通过建立符合试验数据的理论模型，对组合框架的骨架曲线进行参数分析，并在简化二阶分析基础上提出钢管混凝土组合框架的实用恢复力计算模型。通过以上研究可以看出：关于组合框架骨架曲线的试验与理论研究均未考虑节点的半刚性，这必然会导致骨架曲线的计算模型出现偏差。节点的弯矩−转角曲线是获得半刚性组合框架的骨架曲线计算模型的前提。本文作者首先基于参数相关性，运用改进的灵敏度分析方法研究外加强环式钢管混凝土柱−钢梁节点的转动刚度，并与已有的研究进行对比；然后进行半刚性组合框架的参数分析，确定恢复力模型考虑节点半刚性的必要性；最后，运用得出的节点转动刚度计算模型，基于简化二阶分析方法推导出半刚性组合框架骨架曲线的简化实用计算模型。

1 节点弯矩−转角特性

1.1 灵敏度分析方法

忽略各变量间的相关关系有时会得出完全错误的结论[12−13]，因此，考虑参数相关性并基于有限元概率设计分析，在保证参数同时变化的前提下对节点参数进行不确定性灵敏度分析，从而建立节点弹性转动刚度计算模型[14]。此方法不仅结果准确，而且参数的系数具有明确的物理意义。

建立节点弯矩−转角模型关键在于获得节点参数的灵敏度。参数的灵敏度可以由ANSYS PDS模块计算得到。但由于程序本身的限制，有时会导致用于循环计算节点样本质量得不到保证，有时甚至使计算无法进行，且其计算成本较高。

为解决这个问题，本文作者采用组装节点组件的方法，根据样本约束条件来构造灵敏度分析的样本，即采用工程中常用的构件型号，应用 MATLAB建立节点样本，结合多尺度模型，计算参数灵敏度值，主要计算步骤如图1所示。

这种方法的优势为：1) 参数的概率分布无需预先指定，尺寸等参数的概率分布已经隐含在在常用构件中；2) 参数的相关系数无需提前计算；3) 构件无需进行蒙特卡罗抽样。

采用工程中常用的构件建立节点总体样本，符合试验设计的理念。通过随机不重复的抽样方法可以保证计算样本的代表性。

1.2 节点试验分析

陈鹃等[2]进行了外加强环式钢管混凝土柱−钢梁节点静力试验。该试验节点试件取自一栋14层的框剪结构，采用1:3的缩尺比例，结合实际可用的构件尺寸，选取钢管外径×壁厚为159 mm×5 mm，梁采用I16，H175和H198这3种截面。根据钢梁型号将试件分为A，B和C这3组。梁柱均近似按反弯点的位置选取，梁柱长为1 m，加强环的宽度为80 mm，厚度与钢梁翼缘匹配。钢管和型钢梁采用Q235，混凝土为C50。

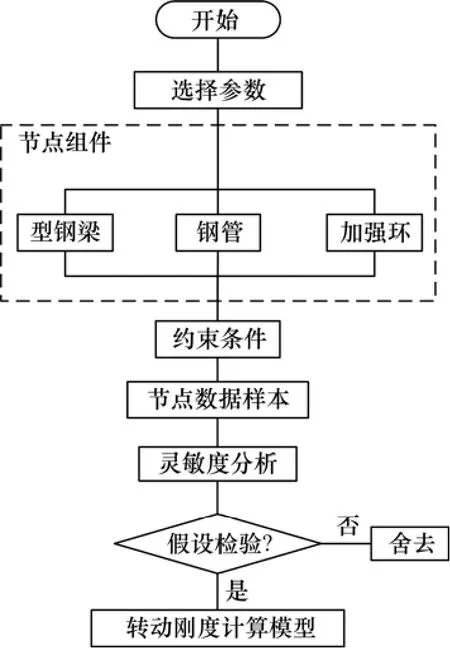
图1 分析步骤Fig. 1 Analysis framework

本文取钢梁型号为 H175的节点试件进行参数灵敏分析，节点的多尺度有限元模型如图2所示。

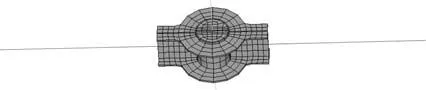
图2 节点多尺度模型Fig. 2 Multi-scale finite element analysis model

为节约灵敏度分析成本，应用多尺度有限元方法。多尺度数值方法在微观力学、结构的损伤识别、健康监测等领域中均有重要的应用。在实际工程中，对于内力复杂、破坏会带来严重后果的关键节点或者局部构件，采用微观模型，可以很好地模拟其屈服、失稳和开裂破坏等特征。而对于梁、板、柱，可以用宏观单元模拟其受力性能，从而节省计算成本。通过合适的方式将二者连接起来，通过协同计算把握结构微观破坏过程和整体受力性能，以便能更好地把握结构的性能。多尺度方法具有精确性和高效性。

建立节点的精细模型和多尺度模型。精细模型采用 SOLID95单元，钢管与混凝土之间的接触采用TARGE170和CONTA175，并且忽略核心混凝土与钢管的相对滑移。多尺度模型的精细模型部分与实体模型相同，宏观模型部分采用BEAM189单元(见图2)。钢材的本构为双线性模型，强化模量为弹性模量的1/100。钢管中的核心混凝土处于三向受压状态，采用DP模型。钢管混凝土宏观单元的本构采用统一理论[15]提出的本构模型。

绘制梁端的荷载−位移曲线并将其与试验数据进行对比，结果如图3所示。多尺度模型与精细模型计算结果基本一致，且与试验数据较吻合，证明了模型的正确性。

1.3 节点灵敏度分析

进行参数灵敏度分析，首先要确定可能影响节点弹性转动刚度的参数。可能影响节点转动刚度的参数有：梁高(hb)、梁宽(wb)、梁翼缘厚(tfb)、梁腹板厚(twb)、加强环宽(dr)、钢管外径(dc)、钢管壁厚(tc)和梁荷载(Lz)。对容量为5 000的样本进行计算，获取参数灵敏度。

为验证循环计算次数是否足够，需要得到参数灵敏度历史图，如图4所示。由图4可知：随着样本数目的增加，参数灵敏度趋于稳定，说明循环计算次数是足够的。

为验证参数灵敏度的正确性，构造t检验统计量。取置信度水平为95%，进行双侧检验。自由度为5 000的t的临界值为1.97，由于梁荷载的t=1.52(＜1.97)，则原假设正确，舍去梁荷载参数。

式中：rp为参数的灵敏度；n为样本自由度。

图4 参数灵敏度历史Fig. 4 Sensitivity history curves

经计算，hb，wb，tfb，twb，dc，tc和 dr所对应的 t检验值分别为45.64，39.10，44.34，43.71，8.22，9.05和11.30；灵敏度 rp分别为0.54，0.48，0.53，0.53，0.16，0.12和0.13；ANSYS PDS模块分析后的灵敏度Kp[14]分别为 0.79，0.05，0.38，0.30，0.52，0.42 和 0.29。通过对比可以看出，本文的方法更加准确。

梁荷载与节点的弹性转动刚度无关，所以灵敏度应为0。本文中梁荷载的rp最小且几乎为0，但是在Kp中梁荷载的灵敏度不为0且大于 wb的灵敏度，故其数值不合理。

1.4 节点弯矩−转角曲线模型

由以上灵敏度分析可得节点弹性阶段弯矩−转角计算模型：

式中：rθ为梁柱相对转角，rad；M为梁端弯矩， N·mm；E0为综合常数，且有E0= 2.8×106。

本文取弯矩−转角计算模型为幂函数模型[16]

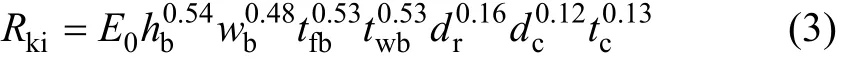
式中：Rki为弹性转动刚度，N·mm/rad。

由于外加强环式钢管混凝土−钢梁节点满足强节点的要求，节点的破坏集中在梁上，所以取节点的极限抗弯承载力为钢梁的塑性极限弯矩。

式中：θr为梁柱相对转角，rad；θ0为塑性相对转角，且 θ0= Mu/Rki，rad； Mu为节点极限抗弯承载力；n为形状参数。

n越大，曲线的形状越尖锐。通过试验数据拟合得到 n为 2.06。结合弹性弯矩−转角关系，可以得到外加强环式圆钢管混凝土−钢梁节点的弯矩−转角曲线计算模型为

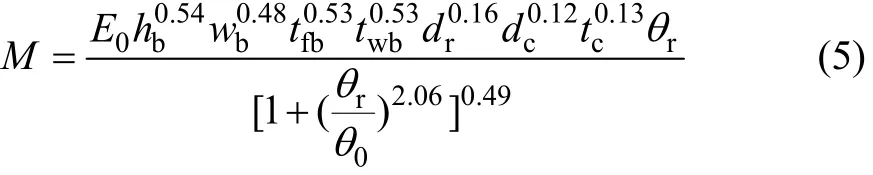
式中：rθ为梁柱相对转角，rad；hb为梁高，mm；wb为梁宽，mm；tfb是梁翼缘厚度，mm；twb为梁腹板厚，mm；dr为加强环的宽度，mm；dc是钢管直径，mm；tc为钢管壁厚，mm。

取上述试验的B组和C组试验结果[2]与理论计算的弯矩−转角曲线进行对比，如图 5所示。理论计算结果与试验数据较吻合，说明弯矩−转角模型精度较高。

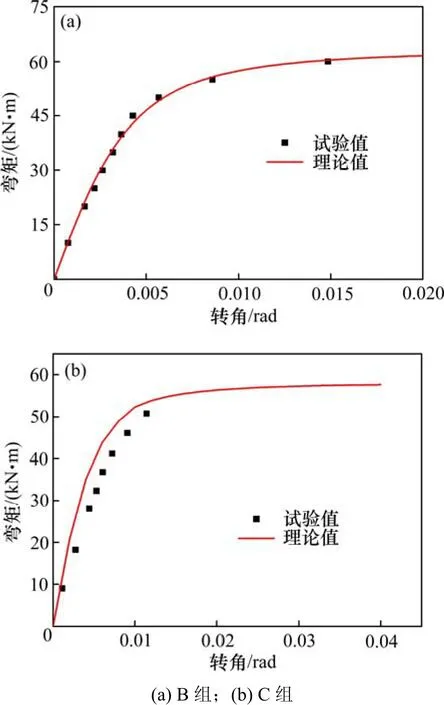
图5 弯矩−转角曲线理论值与试验值对比Fig. 5 Contrast of moment−rotation model curves and test results

2 柔性框架骨架曲线

2.1 骨架曲线试验

王文达等[11]进行了圆钢管混凝土柱−钢梁框架的静力试验。试验包括圆钢管混凝土柱−钢梁框架和方钢管混凝土柱−钢梁框架共4组12榀试件。本文取圆钢管混凝土柱−钢梁框架试件结果进行对比，试件尺寸如表1所示，其中编号为CF-11和CF-21的试件尺寸分别与CF-12和CF-22的完全相同，这里不再列入。

钢材与环板材料相同，材料性能如表2所示。制作混凝土标准试件，在标准条件下养护，测得28 d的立方体抗压强度为42.7 N/mm2。试验进行时，实测立方体抗压强度为52.5 N/mm2。

表1 构件尺寸Table 1 Component dimensions

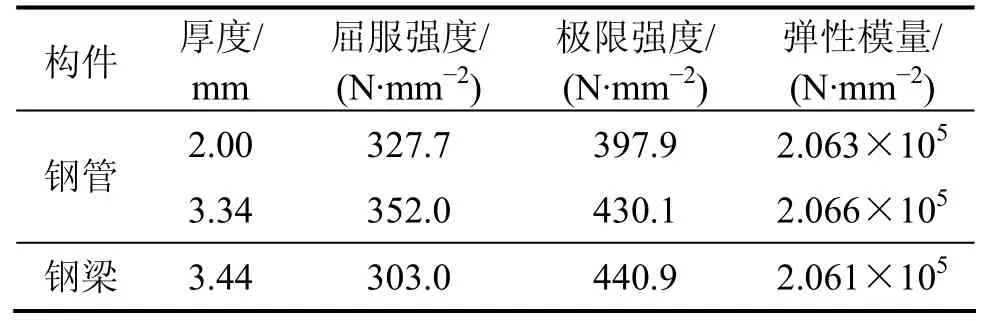
表2 钢材性能指标Table 2 Steel property index

试验的加载方法为：试件屈服前按照位移控制，即 0.25Δy，0.5Δy和 0.75Δy进行加载；试件屈服以后，采用 Δy，1.5Δy，2.0Δy，3.0Δy，5.0Δy，7.0Δy和 8.0Δy加载。其中：Δy为根据限元计算结果取0.7Pmax对应的位移，Pmax为框架的水平极限荷载。研究梁柱线刚度比、轴压比、柱截面含钢率和梁柱长细比对骨架曲线的影响。

2.2 节点半刚性的影响

由于OpenSEES可以较好地模拟组合结构的力学行为[17]，故本文采用OpenSEES建立框架数值模型。梁单元和柱单元均采用基于柔度法的梁柱单元，梁柱连接处采用零长度单元来模拟节点的半刚性。为保证节点的连续性，对梁柱连接处的节点进行平动自由度耦合。由于框架为平面框架，故约束平面外自由度。

应用上文所得外加强环式钢管混凝土柱−钢梁节点弯矩−转角曲线计算模型可得梁柱连接节点的弯矩−转角曲线。钢材的本构采用Steel 02本构模型，混凝土的本构采用Concrete 02本构模型。

将数值模型计算结果与试验结果进行对比，结果如图6所示。其中OpenSEES表示本文数值模拟结果，test为试验结果，NFEMFrame表示未考虑节点半刚性的数值计算结果[11]。

由图6可知数值模拟结果与试验结果较为接近，证明了本文数值模型的正确性。同时，与试验结果相比，未考虑节点半刚性的骨架曲线(即图中NFEMFrame曲线)的刚度偏大，考虑节点柔性的结果(即图中 test曲线)与试验结果更接近。结果表明骨架曲线有必要考虑节点半刚性。

基于CF-13模型，对骨架曲线进行参数分析，以研究节点转动刚度Rk对于框架骨架曲线的影响，结果如图7所示。由图7可知：随着节点转动刚度增大，框架的水平承载力增大，骨架曲线的刚度增大。节点的转动刚度对骨架曲线的下降段斜率也存在影响。节点的转动刚度还反映了梁对于柱的约束情况：当转动刚度增大，框架的整体性增强导致骨架曲线的刚度增大。以上结果进一步证明当计算骨架曲线时，应考虑节点的半刚性。

3 半刚性框架骨架曲线计算模型

假设所有的荷载均作用于节点处，半刚性单层单跨框架计算模型如图8所示。

3.1 柔性梁柱单元刚度矩阵

柔性单元的荷载变形的一般形式如图9所示。

将柔性单元刚度矩阵K分解为一阶刚度矩阵和考虑几何非线性的几何刚度矩阵

式中：K0为一阶刚度矩阵；Kg为几何刚度矩阵。忽略柔性单元的轴向变形可得

图6 骨架曲线理论值与试验值对比Fig. 6 Contrast of moment-rotation model skeleton curves and test results

图7 不同Rk的骨架曲线Fig. 7 Skeleton curves of different Rk

图8 半刚性性框架计算模型Fig. 8 Semi-rigid frame calculation model

图9 半刚性单元Fig. 9 Semi-rigid element

本文框架柱单元的刚度可以直接采用式(7)计算。而框架梁单元中的轴力很小，可以忽略梁单元的二阶效应，即梁单元的几何刚度矩阵为0。

一端柔性连接另一端铰接的半刚性梁单元如图10所示。

图10 半刚性梁单元Fig. 10 Semi-rigid beam element

对于半刚性梁单元可以应用静力凝聚的方式得出其单元刚度矩阵，令式RkE=0，则有

令EM=0，则可得

3.2 计算模型推导

将文中外加强环式钢管混凝土柱−钢梁节点弯矩−转角曲线计算模型作为框架节点的弯矩−转角曲线。为进行理论推导，将该节点的弯矩−转角曲线简化为理想的弹塑性模型，如图11所示。

考虑节点半刚性和几何非线性的影响，采用修正的转角位移方程法[18]，得出水平力P和水平位移Δ之间的关系为

图11 节点弯矩−转角曲线Fig. 11 Moment−rotation curve of connection

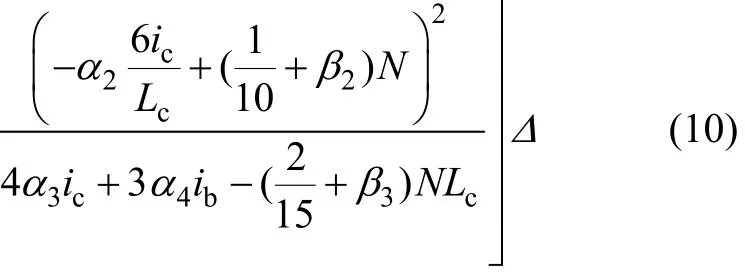
式中：bi和ci分别为梁柱线刚度，N·mm；Lc为柱长，mm。

由式(10)可知：框架弹性侧移刚度与ic，ib，Rk，N和Lc有关，说明节点半刚性是不可忽略的。若忽略节点半刚性，则得出的水平力P和水平位移Δ间的关系退化为

考虑梁柱节点的转动刚度后，框架的水平荷载和水平位移关系，可以看作是将刚接时的矩阵元素进行修正，修正系数分别为iα和iβ。

文中组合框架满足“强柱弱梁”、“强节点弱构件”的要求，梁先于柱破坏，塑性铰先出现在梁上。设框架梁的极限抗弯承载力为 Mpb，则当梁上出现塑性铰时，框架的侧移为

当梁端出现塑性铰时，根据节点的平衡可得柱端弯矩为 Mc= Mb= Mpb，则根据平衡条件可以得出柱底的弯矩为

当水平荷载继续增加时，钢管混凝土柱底将会产生塑性铰。若钢管混凝土压弯构件的极限抗弯承载力为pcM ，则这个过程中产生的柱顶水平位移为

当柱底出现塑性铰之后，框架成为机构，对应骨架曲线出现下降段，此时可采用二阶刚性−塑性铰分析。

式中：1k pk= ；2k qk= 。p和q分别为k1和k2的计算系数，且 1p q+ =。

由于二阶刚性−塑性铰分析忽略了结构的弹性变形，故用增量方程表示下降段荷载增量与位移增量的关系。

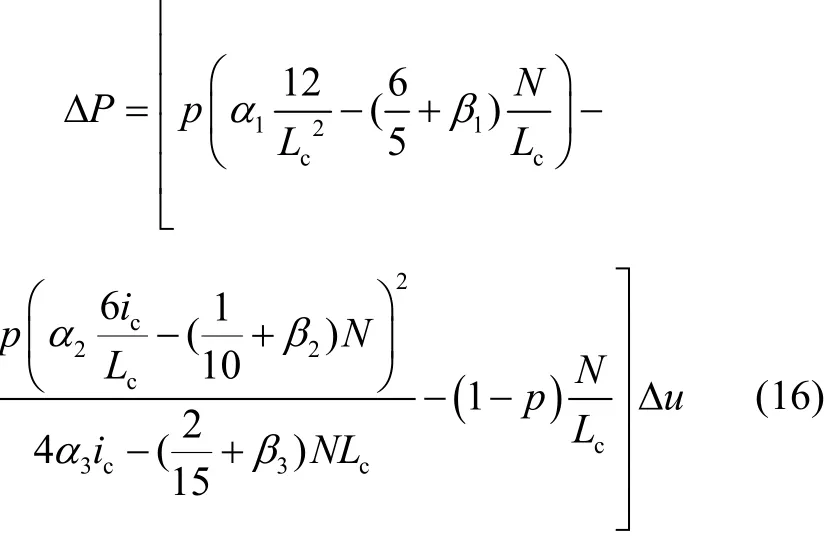
式中：p为圆钢管混凝土柱弯矩−曲率模型的强化模量系数，其取值参考文献[1]中的钢管混凝土构件弯矩−曲率模型来确定。

3.3 实用计算模型

已有的研究表明，钢管混凝土框架的骨架曲线可以采用三折线模型，如图12所示。图12中：正反方向的骨架曲线对称；OA为弹性阶段；AB段为弹塑性阶段；BC为曲线的下降段；Py为屈服承载力；Pu为极限承载力；Ke为骨架曲线的弹性刚度；Kt为曲线下降段斜率。

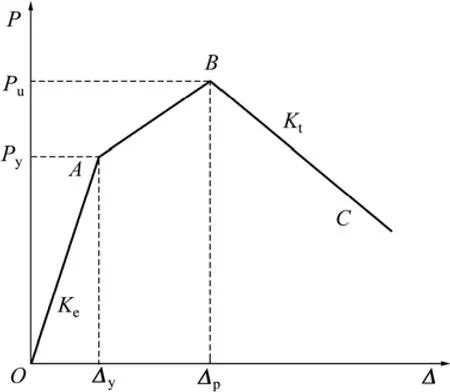
图12 组合框架骨架曲线模型Fig. 12 Skeleton curve model of composite frame

三折线的方程可以表示如下：

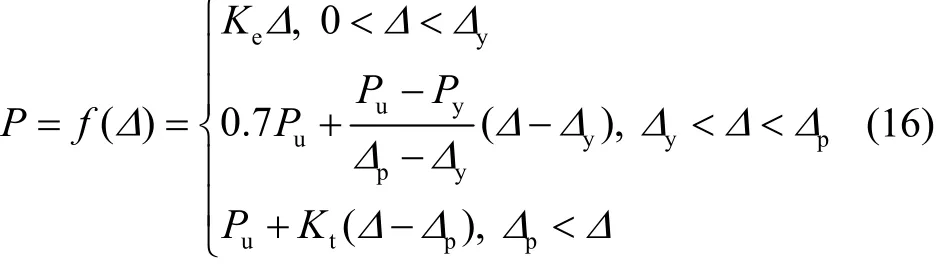
由图12和式(16)可知仅需确定Ke，Δp，Pu和Kt这4个参数便可以得出骨架曲线计算模型。

由上文推导分析可知骨架曲线弹性刚度 Ke和下降段斜率 Kt，且有其中，Pc为相应框架柱的水平承载力，其取值参考文献[19]。此时，框架柱的计算长度系数为

选取CF-12，CF-13，CF-22和CF-23的数值计算结果与理论计算结果进行对比，如图13所示。

由图13可知：与未考虑节点半刚性得出的结果相比，考虑节点半刚性之后的理论计算结果显示的骨架曲线刚度减小，与数值模拟结果更吻合。

图13 骨架曲线对比Fig. 13 Comparison of skeleton curves

4 结论

1) 基于参数相关性，应用 MATLAB与 ANSYS相结合的方法进行参数灵敏度分析，结果更加合理准确。依此建立外加强环式钢管混凝土柱−钢梁节点的弹性刚度计算模型以及节点的弯矩−转角全过程曲线模型。

2) 通过试验数据和参数分析，明确节点的半刚性会降低骨架曲线的弹性刚度和弹塑性阶段负刚度。

3) 考虑节点半刚性，应用二阶分析方法得到的半刚性组合框架骨架曲线的实用计算模型，更加符合组合框架的实际工作性能。

[1] 韩林海. 钢管混凝土结构−理论与实践[M]. 2版. 北京: 科学出版社, 2007: 5−17.HAN Linhai. Concrete filled steel tubular structures: theory and practice[M]. 2nd ed. Beijing: Science Press, 2007: 5−17.

[2] 陈鹃, 王湛, 袁继雄. 加强环式钢管混凝土柱−钢梁节点的刚性研究[J]. 建筑结构学报, 2004, 25(4): 43−49.CHEN Juan, WANG Zhan, YUAN Jixiong. Research on the stiffness of concrete filled tubular column and steel beam joint with stiffening ring[J]. Journal of Building Structures, 2004,25(4): 43−49.

[3] 李成玉, 郭耀杰, 李美东. 钢管混凝土结构外加强环式节点刚性试验研究[J]. 工业建筑, 2006, 36(9): 14−18.LI Chengyu, GUO Yaojie, LI Meidong. Experimental research on the joint stiffness of CFT-Steel beam space joint with outer concentric annular stiffer[J]. Industrial Construction, 2006, 36(9):14−18.

[4] FUKUMOTO T, MORITA K. Elastoplastic behavior of panel zone in steel beam-to-concrete filled steel tube column moment connections[J]. Journal of Structural Engineering, 2005, 131(12):1841−1853.

[5] 孙修礼, 梁书亭, 段友利. 钢管混凝土框架骨架曲线研究[J].地震工程与工程振动, 2007, 27(1): 99−103.SUN Xiuli, LIANG Shuting, DUAN Youli. Research on skeleton curves of concrete filled tubular frame structure[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(1):99−103.

[6] 戚菁菁, 蒋丽忠, 周旺保. 钢−混凝土组合框架结构恢复力模型研究[J]. 中南大学学报:自然科学版, 2013, 44(9):3863−3872.QI Jingjing, JIANG Lizhong, ZHOU Wangbao. Restoring force model of steel-concrete composite frame structure[J]. Journal of Central South University (Science and Technology), 2013, 44(9):3863−3872.

[7] 刘如月, 杨勇, 伊波松,等. 防屈曲偏心支撑混凝土框架结构恢复力模型研究[J]. 工业建筑, 2016, 46(4): 31−35.LIU Ruyue, YANG Yong, YI Bosong, et al. Study on restoring-force model of the eccentrically buckling-restrained braced reinforced concrete frames[J]. Industrial Construction,2016, 46(4): 31−35.

[8] 张向冈, 陈宗平, 薛建阳,等. 钢管再生混凝土框架的恢复力模型研究[J]. 世界地震工程, 2016, 32(1): 277−283.ZHANG Xianggang, CHEN Zongping, XUE Jianyang, et al.Study on restoring force model of recycled aggregate concrete filled steel tube frame[J]. World Earthquake Engineering, 2016,32(1): 277−283.

[9] 王琨, 袁沈峰, 曹大富, 等. 型钢混凝土梁−角钢混凝土柱框架恢复力模型特性研究[J]. 北京理工大学学报, 2014(10):1012−1017.WANG Kun, YUAN Shenfeng, CAO Dafu, et al. Research on hysteretic model of frame sturcture of steel reinforced concrete beams and angle-steel concrete columns[J]. Transaction of Beijing Institute of Technology, 2014(10): 1012−1017.

[10] 王先铁, 周超, 马尤苏夫, 等. 方钢管混凝土平面框架的恢复力模型研究[J]. 地震工程与工程振动, 2014, 34(5): 94−99.WANG Xiantie, ZHOU Chao, MA Yousufu, et al. Study on restoring force model of concrete filled square steel tube planar frames[J]. Transaction of Beijing Institute of Technology, 2014,34(5): 94−99.

[11] 王文达, 韩林海. 钢管混凝土框架实用荷载−位移恢复力模型研究[J]. 工程力学, 2008, 25(11): 62−69.WANG Wenda, HAN Linhai. Research on practical resilience model of load versus displacement for concrete filled steel steel tubular frame[J]. Engineering Mechanics, 2008, 25(11): 62−69.

[12] WANG Zhan, PAN Jianrong, YUAN Jixong, et al. The study on semirigid joint of steel-concrete composite beam to CFST column[J]. Advanced Steel Construction, 2009, 5(4): 421−431.

[13] 董现, 王湛. 基于参数相关性和混合神经网络的结构随机灵敏度分析方法[J]. 建筑结构学报, 2015, 36(4): 149−157.DONG Xian, WANG Zhan. Stochastic sensitivity analysis method based on correlation parameters and hybrid neural network[J]. Journal of Building Structures, 2015, 36(4):149−157.

[14] 潘建荣. 基于相关性的框架节点半刚性分析方法研究[D]. 汕头大学工学院, 2009: 39−48.PAN Jianrong. Analytical method on semi-rigid joint of framework based on correlations[D]. Shantou University.College of Engineering, 2009: 39−48.

[15] 钟善桐. 钢管混凝土统一理论: 研究与应用[M]. 北京: 清华大学出版社, 2006: 36−46.ZHONG Shantong. Unified theory of concrete filled steel tube:research and application[M]. Beijing: Tsinghua University Press,2006: 36−46.

[16] KISHI N, CHEN W F. Moment-rotation relations of semirigid connections with angles[J]. Journal of Structural Engineering,1990, 116(7): 1813−1834.

[17] MAZZONI S, MCKENNA F, SCOTT M H, et al. The open system for earthquake engineering simulation (OpenSEES) user command-language manual[J]. University of California, 2006:34−42.

[18] MORRIS G. Stability design of steel frames[J]. Canadian Journal of Civil Engineering, 1991, 21(1): 171.

[19] DBJ 13-51—2003, 钢管混凝土结构技术规程[S].DBJ 13-51—2003, Technical specification for concrete filled steel tubular structures[S].

Simplified practical calculation method of skeleton curve of semi-rigid composite frame

PAN Jianrong1,2, YANG Zhengting1, WANG Zhan1,2, CHEN Shizhe1

(1. Department of Civil Engineering, South China University of Technology, Guangzhou 510640, China;2. State Key Laboratory of Subtropical Building Science, South China University of Technology,Guangzhou 510640, China)

In view of the calculation model of moment-rotation for composite joints and the composite frame skeleton curve model in which the semi-rigid of the joints is neglected, the calculation methods of the rotational stiffness of the joint and the skeleton curve of the semi-rigid composite frame were investigated. Based on parameter correlation, the parameters sensitivity of outer strengthening ring joint of steel beam to concrete filled steel tubes (CFST) column stiffness were studied by using improved sensitivity analysis method. The stiffness matrix of flexible beam column element was deduced. The calculation model of the moment-rotation curve of the joints was simplified and used to deduce the semi-rigid composite frame. The results show that the improved sensitivity analysis method is more accurate in obtaining the sensitivity of the joint parameters. The semi-rigid joints can decrease the elastic stiffness and slope of the skeleton curve. The skeleton curve model in which semi-rigid joints is introduced is more in line with the actual working performance of the composite frame.

semi-rigid; sensitivity analysis; moment-rotation curve; composite frame; skeleton curve model

TU391

A

1672−7207(2017)11−3013−10

10.11817/j.issn.1672-7207.2017.11.023

2016−12−28；

2017−02−06

国家自然科学基金资助项目(51778241, 51708226, 51378009, 51378219, 51638009)；中央高校基本科研业务费专项资金资助项目(2017BQ086; 2017ZD026)；亚热带建筑科学国家重点实验室基金资助项目(2018ZB35, 2017ZB28, 2017KD22) (Projects(51778241,51708226, 51378009, 51378219, 51638009) supported by the National Natural Science Foundation of China; Projects(2017BQ086, 2017ZD026)supported by the Fundamental Research Funds for the Central Universities; Projects(2018ZB35, 2017ZB28, 2017KD22) supported by the State Key Laboratory of Subtropical Building Science of South China University of Technology)

陈士哲，博士(后)，从事钢结构与组合结构研究；E-mail: ctszchen@scut.edu.cn

(编辑 伍锦花)