一种对薄板焊接全场变形的图像测量方法

龚春园，梁晋，温广瑞，千勃兴

(1. 西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，陕西 西安，710049；2. 广东顺德西安交通大学研究院，广东 佛山，528300)

一种对薄板焊接全场变形的图像测量方法

龚春园1,2，梁晋1,2，温广瑞1,2，千勃兴1,2

(1. 西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，陕西 西安，710049；2. 广东顺德西安交通大学研究院，广东 佛山，528300)

为解决焊接过程中由于高温高亮而使焊件变形难以测量的问题，采用改进的数字图像相关法和双目立体视觉对金属薄板焊接全场变形进行测量。对弱相关图像匹配的解决方法和数字图像相关的算法进行分析，并通过去噪和分段基准保证弱相关图像的正确匹配：首先，使用高斯平滑对原始图像进行去噪处理，消除焊接强光干扰；然后，采用分段建立基准的方法解决了焊点区域因散斑质量下降而出现的难以匹配的问题。对 Newton−Raphson算法的二阶梯度矩阵进行简化，提高相关计算的速度。在测量实验中，首先对板料表面进行预处理与散斑制备，然后在氩弧堆焊(TIG)过程中利用高速相机拍摄板料焊接及冷却自由变形的全过程，最后计算所有图像中变形点的位移，获得板料特别是焊缝区的全场变形数据。研究结果表明：将此方法应用于焊接变形测量，能得到整个焊接过程中任意点的变形曲线，并且可在高温焊缝区获得准确的变形趋势。测量结果可用于分析影响焊接变形的因素，进而对焊接变形实施控制，也可用于检验焊接变形数值模拟方法的正确性。

数字图像相关；双目立体视觉；薄板焊接；全场变形；分段基准

大型轻质化是当代焊接结构的发展趋势，薄壁材料越来越多地应用于汽车、飞机、轮船等制造行业，在这些结构的焊接过程中，焊接变形是影响焊接产品加工精度、外部形状和结构性能的重要因素，是工业生产中迫切需要解决的问题。邓德安等[1−2]研究了焊接接头的残余应力；WANG 等[3−4]在针对工件进行的研究中指出焊接过程中的纵向收缩在焊缝周围引起的压缩应力是使试板发生变形的主要原因。采用有效可靠的测量方法研究试板焊接过程中的动态变形，分析影响焊接变形的因素，并寻求在焊接过程中或者焊后冷却过程中控制焊接变形的方法具有重要意义。国内外学者对薄板焊接变形进行的研究，大都基于有限元分析。ASEL等[5]采用黏弹塑性模型模拟了薄壁铝合金T形接头在焊接过程及焊后的局部和全场失稳应变，运用结构模型和特征值失稳分析来研究焊件的全局失稳变形。LUO等[6]采用基于固有应变的弹性有限元方法对 3D薄板结构进行焊接失稳模拟。采用数值模拟方法预测焊接件的焊接变形和应变，一般忽略焊接时的复杂因素，比如焊接变形机理的复杂性、高温时材料参数的难以测定性等，预测结果一般与实验结果相差较大。在实验测量方面，采用接触式传感器如应变计、位移传感器等传统的测量方法，不能测量焊接件表面整体的变形场。在焊缝区域这种高温短时环境下，变形的速度较快，变形量较大，接触式测量设备需要耐高温，测头的位置不能阻挡焊枪轨迹，因此，难以充分接近焊缝区域，故这种方法使用受限。目前，基于双目立体视觉和数字图像相关(digital image correlation，DIC)[7−8]这种非接触式测量方法逐渐得到了广泛的应用，该方法通过比较变形前后所采集图像的灰度变化来测量物体表面的变形场。然而，使用这种方法对金属薄板焊接过程中全场变形进行测量也存在问题。由于焊接环境比较恶劣，焊接过程产生的高温高亮现象将极大地影响所采集图像的质量，导致图像亮度不均衡、模糊，这种状况在靠近焊点的焊缝区域尤为严重，造成相关计算过程中图像难以匹配，计算中断。本文作者对数字图像相关算法在高温弱相关环境下的匹配方法进行研究，通过对图像匹配前进行滤波处理，同时自适应建立分段基准，不仅使相关计算过程能够正常进行，而且这种处理对焊缝区域等干扰较大的部位也能够更大程度地完成匹配，使计算区域更接近焊点位置，扩大测量区域能够显示的范围。

1 高温弱相关环境下图像的匹配策略

1.1 数字图像相关法

数字图像相关法，先在待测表面制造随机散乱的图案用于标记定位。设图1中R区域为制造好的散斑区域，在其上划定1个像素长度为M的方形子区S，通过相似度计算，找出这块子区在变形后图像上的对应子区 S′，S和 S′上对应点的坐标差就是该点的变形量。可以看出，该方法做出了2点假设：在变形过程中，任何1点的灰度始终保持不变；在子区足够大的情况下，其待匹配图像中有且只有 1个子区能与之对应。

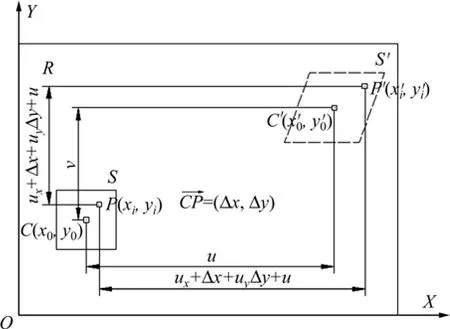
图1 数字图像相关原理Fig. 1 Principle of digital image correlation

由于要进行子区追踪，该方法最主要的问题是相似性判断，建立相关函数来衡量2个子区的相似程度，通过求取相关函数的极值来锁定目标子区。本文使用的是零均值归一化最小距离平方和相关系数，如式(1)所示，该函数对线性光强的灰度变化不灵敏，具有一定的抗干扰能力[9]。以 ZNSSD C 表示零均值归一化最小距离平方和系数，其计算公式为

定义映射函数以描述参考图像子区内所有像素点的变形和运动，常采用一阶函数[10−11]表示，如下式所示：

式中：u和v分别为图像子区中心点 ( x0, y0)变形后在x和 y方向的位移； ux， uy， vx和 vy为参考子区的位移梯度。

1.2 弱相关图像的高斯滤波及分步匹配

在薄板焊接过程中，由于测量环境受限，焊枪产生的亮点使焊接散斑图像光照不均匀，环境强光会在测量物体表面引起光噪声，焊接强光噪声往往会使图像发生区域性亮度的突然改变，影响焊接图像匹配。另外，由于焊枪位置堆积了大量能量，其所在区域温度升高至上千摄氏度，会使焊接金属熔融区的焊接散斑发生微小的脱落、变色和变形，导致散斑质量的降低。因此，焊接高温环境的产生的亮度不均和散斑变色将阻碍散斑的正常匹配。

针对红热和高亮以及环境光产生的噪声，当相关计算进行至焊接强光干扰较为强烈的区域时计算无法正常进行。为此，对原始图像采用高斯平滑滤波处理。高斯滤波器是1类根据高斯函数的形状来选择权值的线性平滑滤波器。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。图2(a)所示为原始图像，图2(b)所示为采用高斯平滑处理以后的图像，由图2可知：采用高斯平滑处理后的图像对比度显著增强，这有助于相关计算时图像子区的成功匹配。

图2 采用高斯平滑处理的前后图像对比Fig. 2 Comparison of images using Gaussian smoothing or not

对光干扰较为强烈的区域进行降噪处理后，在焊接强光干扰较为强烈的区域内2个较为接近状态的相关计算可正常进行。但是，焊点区域散斑发生微小的氧化脱落、变形等，散斑质量降低，仅仅依靠原始图像作为参考，待匹配的变形图像与参考图像之间的相似程度大大降低，仍然不利于图像的相关计算。梁晋等[12]在使用数字图像相关法进行板料冲压变形的测量时，考虑到相邻状态变形的连续性，针对大变形提出分步匹配算法，采用每隔若干个状态手动添加1次基准的方法完成变形计算。在此基础上，基于相邻弱相关图像的相似性，在图像序列中自动建立基准，避免手动操作的繁琐，同时也能够保证建立的基准数目最少，将精度损失降到最低。

在尽量增加变形过程采样的频率后，采用分段自适应建立基准的方法保证相关图像能够正常匹配。如图3所示，其匹配过程如下。

1) 以初始状态I1(Ik1)为基准，自I2开始均与I1进行相关计算，直到某个状态与I1匹配失败，将该状态的前1张状态定为新的基准状态Ik2。

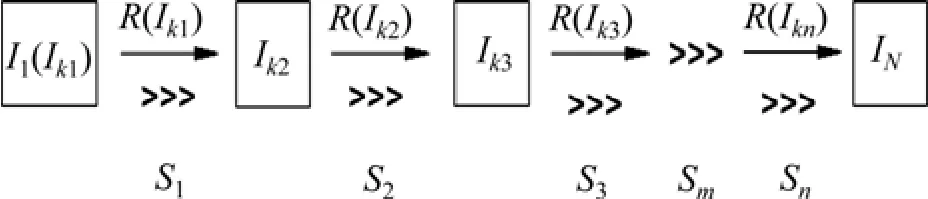
图3 图像分段匹配示意图Fig. 3 Schematic diagram of image piecewise matching

2) 以Ik2为基准，自Ik2+1状态开始，后面的状态均与之匹配，若遇到匹配失败的状态，将失败状态前1张状态Ik3再设为基准进行相关计算；

3) 以此类推，图像子区的追踪过程被分为 S1，S2，…，Sn个区域，一共对整个状态序列建立n个基准，这样就可以解决变形状态与初始状态相差很大而无法匹配的问题。

变形中状态的变形量是一个阶段变形量的累加和，如下式所示：

式中：ξ ( Ip,Ikm)是在Sm段以Ikm为基准Ip对应位置的变形量； ξ ( Si)表示在 Si这段状态序列，首尾 2张状态对应点的位移差，即该段的最大变形量。

多次建立基准会导致累积误差，其数学期望可描述为

式中：H1，H2，…，Hn为每个子段的匹配次数；δ为2个状态匹配的偏差。

通过对图像的高斯滤波处理和分段建立基准，可以完成弱相关图像的相关计算。

1.3 快速迭代计算

上述方法可以解决弱相关图像的匹配问题，为了加快求解速度，以下讨论对相关计算中迭代简化的问题。

采用ZNSSD相关系数作为图像相关匹配的准则，则优化的目标为式(1)最小，其中p为u，ux，uy，v，vx和vy的函数。

采用 N−R(Newton−Raphson)算法对式(1)进行迭代求解，则有

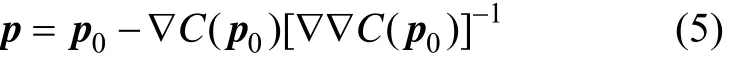
式中：p0为待求解未知数的初值，通过整像素搜索获得；p是下一步迭代的近似解；0()C∇p和0()C∇∇p分别为一阶和二阶梯度，由于每一步迭代过程都要对这2个矩阵进行计算，为了提高计算速度，将一阶梯度和二阶梯度[13−14]近似表示为：

2 实验装置

2.1 实验方案

本次实验完成对薄钢板焊接变形的测量，由于传统的位移计测量的结果基本是准确的，因此，先用图像方法得到的结果与位移计测量结果进行对比，验证改进的数字图像相关法的合理性；在图像方法被验证可行的基础上，分析获得的全场数据，研究变形过程。

为了实现上述实验目的，设计图4所示的测量与实验系统布局进行钢试件的焊接实验。验证实验和全场测量在同一次实验中进行。图中位移传感器组构成传感器测量系统，位于钢板的上表面，3个传感器由电缆引向计算机终端，采集的数据由1台计算机实时获取。由双目相机构成图像测量系统，负责对钢板下表面进行拍照，将图像实时存储。在实验中选择BWG3−20 mm电感调频式位移传感器，其测量范围为0～20 mm；分辨率为0.004 mm/mV；非线性相对误差为 0.27%；重复性相对误差为 0.02%。在焊接条件下传感器的测量相对误差小于 0.15%，能够满足焊接瞬态变形测量的精度要求。在实际的测量环境中，相机横梁和焊缝平行。

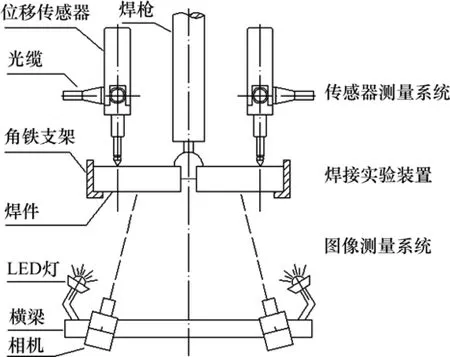
图4 实验系统示意图Fig. 4 Schematic diagram of experiment system

2.2 真实环境

本实验对厚度为2.5 mm的Q235长方形薄板进行焊接过程中的应变测量，板的规格及位移计观察点的布局如图5所示，焊接顺着Y的正方向进行。

利用漏板在喷砂后的被测表面用黑白高温漆制造散斑特征：在焊缝区域形成分布均匀的白点，其余区域覆盖为白底黑点的图案，完成喷涂处理后的薄板如图 6(a)所示，图 6(b)所示为实验现场照片。实验采用TIG(tungsten inert gas)焊接方式，电压为12.5 V，电弧电流为 100 A，氩气流量为 10 L/min，钨棒直径为2 mm，行进速度为5 mm/s。自焊接开始至焊接完成后7 min的时间段，采用自行研发的XTDIC测量系统采集薄板的背面图像，所用的2个Basler相机的分辨率为1 920像素×1 200像素，镜头焦距为16 mm。

图5 板件坐标系以及焊缝区域的CAD模型图Fig. 5 Coordinate system of plate and CAD model of weld area

图6 预处理试件及实验现场照片Fig. 6 Pretreatment of test-piece and photo of experimental scene

3 实验分析

3.1 对比验证

实验结束后，将图像方法和位移计方法在3个测量点处获得的面外变形情况用曲线绘制，如图7所示。由图7可知：2种方法的测量结果基本一致。两者存在的误差主要是：1) 测量仪器本身的精度相异；2) 2种方法测量的分别是焊接件的正面和背面，在实验过程中，正面和背面的温度场存在微小不同，导致引起的变形也有差异；3) 对12个点的标记是手工完成的，不可能做到正、反面对应标记点完全对正。

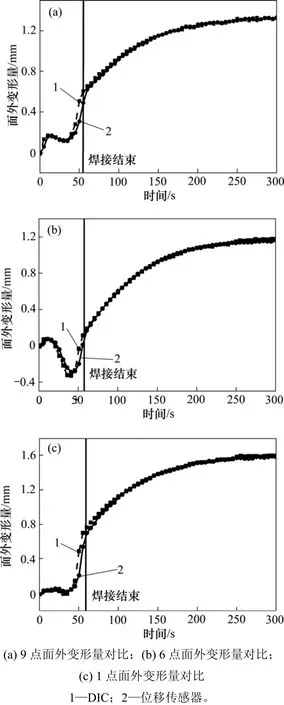
图7 2种测量方法结果对比Fig. 7 Comparison of 2 measurement methods

实验表明，本文作者提出的测量方法能够准确地描述焊接过程中试件表面的变形状况，可以将测量结果中其余位置的全场信息用作分析。

3.2 全场变形分析

利用上述实验装置和计算方法，对Q235钢板焊接测量计算完成后，截取焊接和冷却过程中3个方向上的位移场，如图8所示。由于焊接相变，液态金属无法承受任何负载，各点的位移变化比较复杂；特别是接近焊点的光亮处，由于数字图像相关法在此处不能很好地匹配，在焊点周围出现残缺。

从图8可以看出：在焊接过程中，Z方向(面外方向)的变形量以焊点为中心向四周逐渐减小，离焊点近处产生正向变形位移(方向为竖直向下)，沿焊缝方向的两侧边缘处产生负向位移；焊接刚结束时，越靠近焊缝，变形量越大，板料中心偏右的焊缝区处的变形最大；冷却结束后，Z向位移出现明显的马鞍形状，沿焊缝方向的边缘区域位移为正值，靠近焊缝处达到最大，沿板料宽度方向的边缘区域位移为负值，越靠近边缘，沿负方向的变形量越大。在焊接过程中，Y方向除了焊缝区变形比较大以外，其余部分变形均匀，产生少量的正向位移。在焊缝区域，整个焊接和冷却过程中，焊缝上端产生负向位移，下端产生正向位移。冷却结束后，变形均匀。X方向的变形趋势与Z方向的基本一致。

焊接变形主要是由于不均匀温度场导致热源周围的金属运动产生的。在焊接过程中，接近热源位置的金属温度较高而迅速膨胀，以热源为中心，距离热源越远的位置热影响越小，产生的热变形越小，因此，薄板自外向内产生挤压作用；同样，当热源离开时，该区域的温度降低，开始收缩，远离热源的区域对它又产生拉伸作用。

从图8还可以看出：薄板产生的横向收缩变形和弯曲变形比较明显；在焊接过程中，焊点区域的温度骤升，在焊件厚度方向上温度分布不均匀，产生横向残余应力，引起横向收缩变形，使焊件在垂直于焊缝方向的尺寸比焊前的短，且从中心向两端递减；由于焊缝及其附近金属的纵向收缩变形在焊接薄板厚度方向上分布不均匀，产生了弯曲变形。

图8 薄板件表面三维位移场Fig. 8 3D displacement field on thin plate surface

4 结论

1) 针对焊接过程的弱相关图像匹配算法提出改进，通过去噪和建立分段基准的方法，能够较可靠地计算薄板件在整个焊接过程中表面的变形场，为研究焊接变形规律提供了一种有效的手段。

2) 对相关匹配过程中大型矩阵的计算，采用Newton−Raphson算法简化了其二阶梯度矩阵，提高了相关计算的搜索速度，实现了快速迭代计算。

3) 对Q235钢板焊接测量可以看出：焊缝区变形量最大，冷却后Z向位移出现明显的马鞍形状；薄板产生较明显的横向收缩变形和弯曲变形。

[1] 邓德安, 张彦斌, 李索, 等. 固态相变对P92钢焊接接头残余应力的影响[J]. 金属学报, 2016, 52(4): 394−402.DENG Dean, ZHANG Yanbin, LI Suo, et al. Influence of solid-state phase transformation on residual stress in P92 steel welded joint[J]. Acta Metallurgica Sinica, 2016, 52(4): 394−402.

[2] 薛鹏, 张星星, 吴利辉, 等. 搅拌摩擦焊接与加工研究进展[J].金属学报, 2016, 52(10): 1222−1238.XUE Peng, ZHANG Xingxing, WU Lihui, et al. Research progress on friction stir welding and processing[J]. Acta Metallurgica Sinica, 2016, 52(10): 1222−1238.

[3] WANG Jiangchao, SHIBAHARA M, ZHANG Xudong, et al.Investigation on twisting distortion of thin plate stiffened structure under welding[J]. Journal of Materials Processing Technology, 2012, 212(8): 1705−1715.

[4] WANG Jiangchao, YIN Xianqing, MURAKAWA H.Experimental and computational analysis of residual buckling distortion of bead-on-plate welded joint[J]. Journal of Materials Processing Technology, 2013, 213(8): 1447−1458.

[5] ASEL M, NAMI M, KADIVAR M H. Prediction of welding buckling distortion in a thin wall aluminum T joint[J].Computational Materials Science, 2007, 38(4): 588−594.

[6] LUO Yu, DENG Dean, JIANG Xiaoling. Prediction of welding distortion during assembly process of thin plate structures[J].China Welding, 2005, 14(2): 153−157.

[7] 唐正宗, 梁晋, 肖振中, 等. 用于三维变形测量的数字图像相关系统[J]. 光学精密工程, 2010, 18(10): 2244−2253.TANG Zhengzong, LIANG Jin, XIAO Zhenzhong, et al. Digital image correlation system for three-dimensional deformation measurement[J]. Optics and Precision Engineering, 2010, 18(10):2244−2253.

[8] 胡浩, 梁晋, 唐正宗, 等. 数字图像相关法测量金属薄板焊接的全场变形[J]. 光学精密工程, 2012, 20(7): 1636−1644.HU Hao, LIANG Jin, TANG Zhengzong, et al. Measurement of full-field deformations in metal sheet welding processes by image correlation method[J]. Optics and Precision Engineering,2012, 20(7): 1636−1644.

[9] PAN Bing, XIE Huimin, WANG Zhaoyang. Equivalence of digital image correlation criteria for pattern matching[J]. Applied Optics, 2010, 49(28): 5501−5509.

[10] PAN Bing, QIAN Kemao, XIE Huimin, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review[J]. Measurement Science & Technology,2009, 20(6): 152−154.

[11] LU H, CARY P D. Deformation measurements by digital image correlation: implementation of a second-order displacement gradient[J]. Experimental Mechanics December, 2000, 40(4):393−400.

[12] 梁晋, 胡浩, 唐正宗, 等. 数字图像相关法测量板料成形应变[J]. 机械工程学报, 2013, 49(10): 77−83.LIANG Jin, HU Hao, TANG Zhengzong. Digital image correlation method for strains measurement of metal sheet forming[J]. Journal of Mechanical Engineering, 2013, 49(10):77−83.

[13] BOLTE J, BAUSCHKE H, TEBOULLE M. A descent Lemma beyond Lipschitz gradient continuity: first-order methods revisited and applications[J]. Mathematics of Operations Research, 2016, 42(2): 330−348.

[14] SHI Wei, LING Qing, WU Gang, et al. Extra: an exact first-order algorithm for decentralized consensus optimization[J]. Siam Journal on Optimization, 2014, 25(2): 944−966.

An image measurement method of whole field deformation during thin plate welding process

GONG Chunyuan1,2, LIANG Jin1,2, WEN Guangrui1,2, QIAN Boxing1,2

(1. State Key Laboratory for Manufacturing Systems Engineering, School of Mechanical Engineering,Xi’an Jiaotong University, Xi’an 710049, China;2. Guangdong Shunde Xi’an Jiaotong University Academy, Foshan 528300, China)

It is hard to measure the deformation due to the high temperature and highlight during the welding process. To solve this problem, a method based on the modified digital image correlation and binocular stereovision technology were used in the thin plate welding whole field deformation. The solution to match images of poor correlation and the algorithm of digital image correlation were analyzed, and both the noise disposal and step benchmark were adopted to ensure that the images of poor correlation could be matched correctly. Firstly, Gaussian smoothing was used to deal with the noise of original image; then a method of setting up the piecewise benchmarks was adopted to overcome the matching difficulties which were caused by eliminate the effect of welding light, and the weak speckle performance around the solder joint. In order to improve the speed of correlation calculation, the second order gradient matrix was simplified by Newton−Raphson algorithm. After the metal surface pretreatment and speckle preparation, some photos of tungsten insertgas (TIG) arc welding and cooling process were taken by the high speed cameras during the whole states of deforming in the experiment. Eventually, the displacements of deformation points in all images could be calculated so that the data of whole field dynamic deformation on the thin plate especially the welding zone could be obtained. The results show that this method can get the strain curves of arbitrary points in the whole welding process, and the accurate deformation trend of the high temperature welding area can also be obtained. The measuring results can be used to analyze the influence factors of welding deformation, control the welding deformation and verify the welding numerical simulation.

digital image correlation; binocular stereovision; thin plate welding; whole field deformation; piecewise benchmark

TG404；O353.5

A

1672−7207(2017)11−2935−07

10.11817/j.issn.1672-7207.2017.11.013

2016−11−19；

2016−12−15

国家自然科学基金资助项目(51675404，51421004)；广东省公益研究与能力建设专项资金资助项目(2014A010104003)(Projects(51675404, 51421004) supported by the National Natural Science Foundation of China; Project(2014A010104003) supported by the Public Research and Capacity Building Special Funds of Guangdong)

梁晋，教授，博士生导师，从事机电控制、机器视觉等研究；E-mail: liangjin@mail.xjtu.edu.cn

(编辑 刘锦伟)