张应变和N型掺杂对锗能带结构的调节

周志文，郭海根，李世国，沈晓霞，王颖

（1.深圳信息职业技术学院 电子与通信学院，广东 深圳 518172;2.深圳信息职业技术学院离退休工作委员会办公室，广东 深圳 518172）

【博士论坛】

张应变和N型掺杂对锗能带结构的调节

周志文1，郭海根2，李世国1，沈晓霞1，王颖1

（1.深圳信息职业技术学院 电子与通信学院，广东 深圳 518172;2.深圳信息职业技术学院离退休工作委员会办公室，广东 深圳 518172）

基于体锗的能带结构，从理论上计算分析了张应变和N型掺杂对锗能带结构的调节。张应变使价带和导带的能级分裂、偏移，N型掺杂使费米能级偏移，从而将锗调节为准直接带隙材料。当单独引入0.018的张应变时，锗变为准直接带隙，直接带隙为0.53 eV。当单独掺杂N型杂质9.5×1019cm-3时，锗的费米能级到达Γ带底。引入适量的张应变和N型掺杂浓度，既有利于锗能带结构的调节，又有利于材料的实际制备。研究结果为锗发光器件的设计和制作提供借鉴。

锗；张应变；n型掺杂；能带；发光器件

引言

制备兼容于硅（Si）互补金属-氧化物-半导体（CMOS）工艺的发光管，甚至激光器，从而实现电子器件和光电器件的片上集成，是近年来学术界和产业界的研究热点和难点[1]。由于硅是间接带隙材料，硅的发光效率极其低下。为此，人们提出了多种新型材料和结构，如多孔硅、纳米硅、掺铒（Er）硅、硅基锗（Ge）薄膜等等[2]。由于锗与硅的兼容性好，锗在硅基光电集成中发挥了重要作用。已经成功研制了锗的光电探测器[3]、光电调制器[4]以及场效应晶体管[5]。然而，锗的发光器件依然面临一些挑战，比如发光效率较低，阈值电流较高，实用的锗激光器仍需继续研究[6]。

本文基于体锗的能带结构，从理论上计算分析了张应变和N型掺杂对锗能带结构的调节。通过适量的张应变和N型掺杂，可以调节锗的能带结构，控制电子的分布，实现锗的直接带隙。

1 体锗的能带结构

室温下，体锗的能带结构如图1所示[7]。锗的价带由轻空穴带（LH）、重空穴带（HH）和自旋轨道分裂带（SO）组成。轻空穴带和重空穴带在波矢量k＝0即Γ点处简并，并且取得价带最大值。价带的自旋轨道分裂能ESO＝0.29eV。导带的最小值在波矢量k＝＜111＞即L点处取得，另外在Γ点处有极小值。导带在Γ点附近的区域称为Γ能谷，在L点附近的区域称为L能谷。因为导带最小值和价带的最大值不在相同的k值，锗的能带为间接带。锗的间接带隙EgL0＝0.664 eV，直接带隙EgΓ0＝0.8eV。直接带隙与间接带隙的差值为0.134 eV。

图1 室温下体锗的能带结构Fig.1 Bulk Ge band structure at room temperature

由于锗的间接带能带特性，根据费米—狄拉克分布函数，电子主要分布在导带的L谷，空穴主要分布在价带的Γ顶附近，如图1所示。由于电子和空穴的分布不在相同的k值，基于能量守恒和动量守恒原理，导带电子和价带空穴的复合需要声子参与，导致锗的辐射复合效率较低。提高锗的辐射复合效率，需要对体锗的能带结构进行调节，使导带的Γ谷有电子填充分布（L谷是否有电子分布取决于能带结构）。

2 张应变对锗能带结构的调节

应变是调节能带结构的一种有效手段。张应变使能带退简并，能级偏移，最终使带隙变小。根据形变势理论，在双轴张应变作用下（张应变分量εxx、εyy和εzz的关系有：εyy＝εxx，εzz＝－2C12/C11εxx），导带L带底到轻空穴带LH带顶的带隙EgLlh，导带L带底到重空穴带HH带顶的带隙EgLhh，导带Γ带底到轻空穴带LH带顶的带隙EgΓlh，以及导带Γ带底到重空穴带HH带顶的带隙EgΓhh可以分别表示为[8]

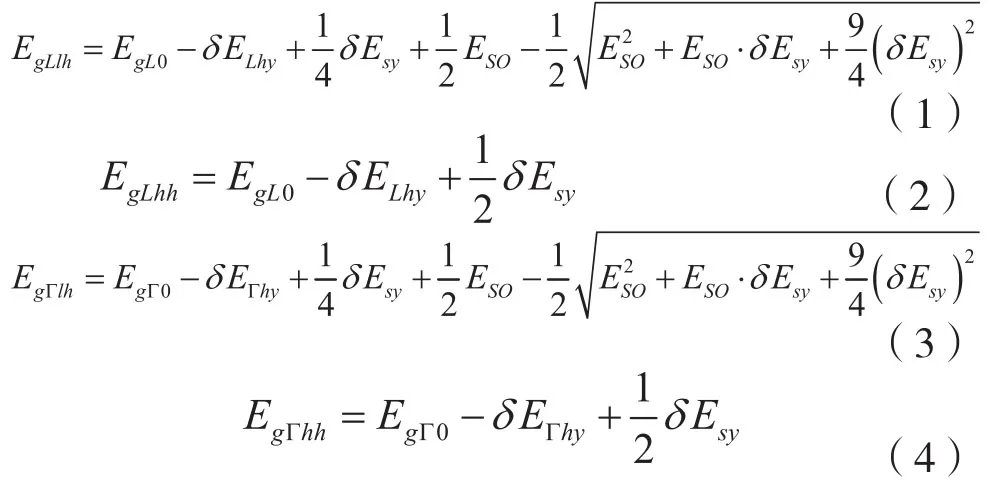
其中，EgL0、EgΓ0、ESO分别为无应变时锗的间接带隙、直接带隙和自旋轨道分裂带隙。室温时，EgL0＝0.664 eV，EgΓ0＝0.8 eV，ESO＝0.29 eV。δELhy和δEΓhy分别为L带和Γ带的静压形变势。δEsy为剪切形变势。δELhy、δEΓhy和δEsy与张应变分量εxx的关系分别表示为

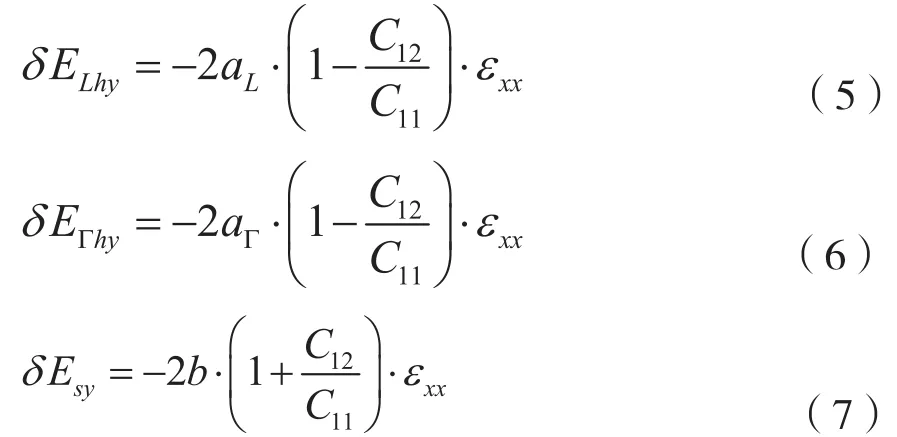
其中，aL和aΓ分别为L带、Γ带的静压应变参数，b为单轴应变参数。并且有aL＝－2.78 eV，aΓ＝－8.97 eV，b＝－1.88 eV。C11和C12为锗的弹性常数，C11＝128GPa，C12＝48GPa[8]。

间接带隙（EgLlh和EgLhh）和直接带隙（EgΓlh和EgΓhh）与张应变（εxx）的关系如图2所示。由图可知，张应变作用下，轻空穴带和重空穴带退简并，并且轻空穴带的能级比重空穴的高，使得直接带隙为导带Γ带到轻空穴带顶的能级差，即EgΓlh，直接带隙为导带L带到轻空穴带顶的能级差，即EgLlh。另外，随着张应变的增加，四种带隙值均变小，但是直接带隙EgΓlh的减小量比间接带隙EgLlh的大。当εxx＝0.018时，直接带隙与间接带隙相等，即EgLlh＝EgΓlh＝0.53 eV。当张应变εxx＜0.018时，四个带隙中的最小值为EgLlh，锗为间接带隙材料；当张应变εxx＞0.018时，四个带隙中的最小值为EgΓlh，锗为直接带隙材料。当锗的能带结构被张应变调节为直接带隙时，电子将优先分布在Γ谷，利于与价带顶Γ点附近的空穴进行辐射复合（不再需要声子参与，复合几率增加）。电子和空穴的辐射复合能量为直接带隙EgΓlh，即0.53 eV。

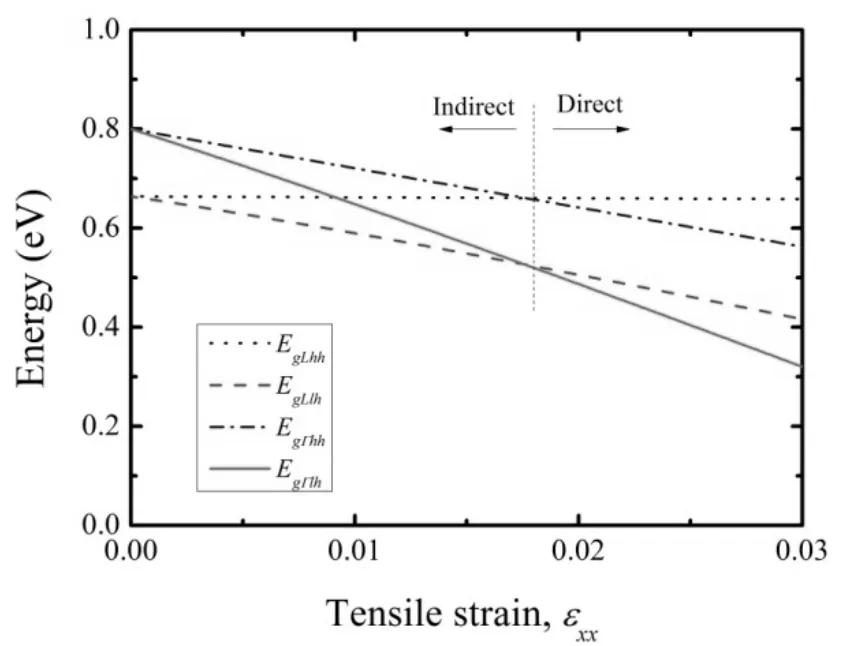
图2 能带与张应变的关系Fig.2 Relationship between energy and tensile strain

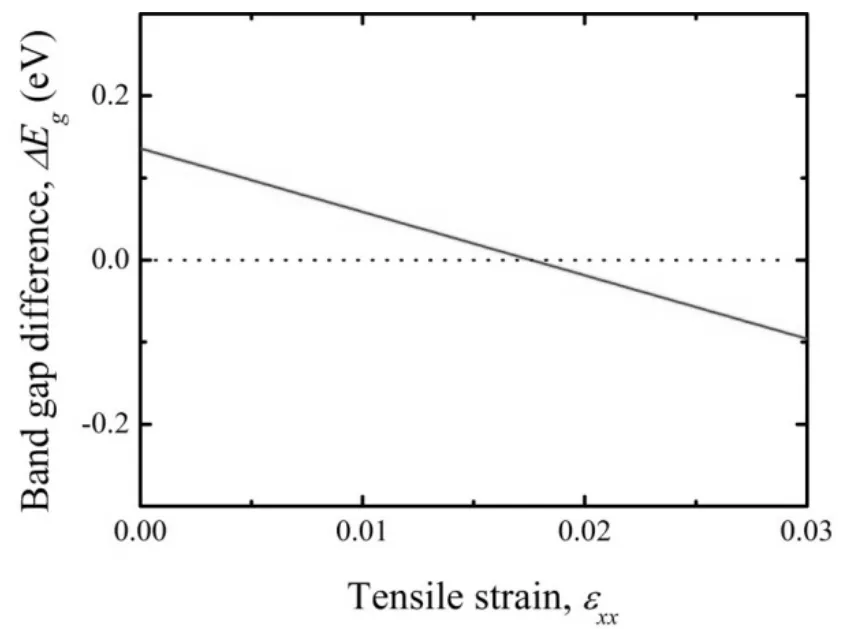
图3 带隙差与张应变的关系Fig.3 Relationship between band gap difference and tensile strain

图3为直接带隙EgΓlh和间接带隙EgLlh的差值ΔEg（ΔEg＝EgΓlh－EgLlh）与张应变（εxx）的关系。张应变为εxx＝0时，ΔEg＝0.136 eV；张应变为εxx＝0.018时，ΔEg＝0。ΔEg随着张应变εxx的增加近似线性减小。ΔEg对电子在Γ谷和L谷的分布几率和浓度具有重要影响。

3 掺杂对锗能带结构的调节

掺杂主要是调节锗能带结构的费米能级。室温下，体锗的本征载流子浓度ni＝2×1013cm-3。以价带顶EV为能量的参考0点，即EV＝0 eV，则导带底L点的能量EL＝0.664 eV，Γ点的能量EΓ＝0.8 eV，本征费米能级EFi＝0.32 eV。

在体锗中掺杂N型杂质，N型锗的费米能级EFn随着掺杂（电子）浓度n0的增加而增大（向导带EL靠近）。根据费米—狄拉克分布函数以及态密度与能级之间的关系，得到n0与EFn的关系为[9]

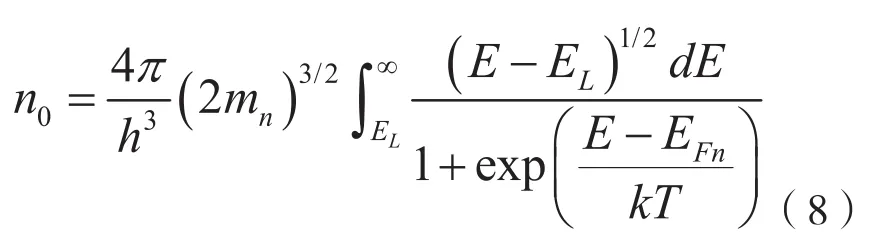
其中，h为普朗克常数，h＝6.625×10-34J·s，k为玻尔兹曼常数，k＝1.38×10-23J/K，T为温度，T＝300 K，mn为电子的态密度有效质量，mn＝0.55m0。m0为自由电子质量，m0＝9.11×10-31Kg。当掺杂浓度较低时，费米能级在禁带内，掺杂为非简并掺杂，电子主要分布在L谷；当掺杂浓度较高时，费米能级进入导带，掺杂为简并掺杂，此时需要同时考虑电子在L谷和Γ谷的分布。在此情况下，公式（8）改写为：

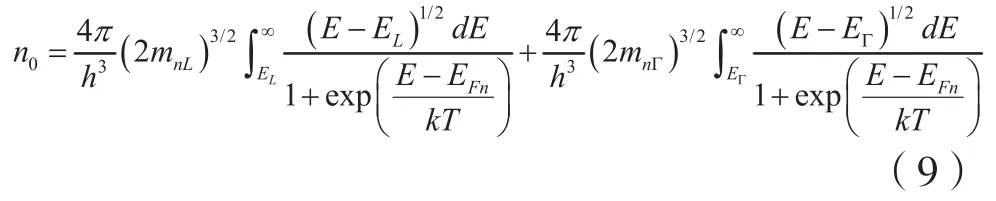
mnL和mnΓ分布为L谷和Γ谷电子的态密度有效质量，[7-9]。

在体锗中掺杂P型杂质，P型锗的费米能级EFp随着掺杂（电子）浓度p0的增加而减小（向价带EV靠近）。根据费米—狄拉克分布函数以及态密度与能级之间的关系，得到p0与EFp的关系为[9]

其中，mp为空穴的态密度有效质量，mp＝0.34m0（mp包含轻空穴质量mpl＝0.043m0和重空穴质量mph＝0.33m0

[7,9]）。当掺杂浓度较低时，费米能级在禁带内，掺杂为非简并掺杂；当掺杂浓度较高时，费米能级进入导带，掺杂为简并掺杂。

费米能级EFn与掺杂浓度n0的关系以及费米能级EFp与掺杂浓度p0的关系如图4所示。对于P型掺杂，当p0＝3×1018cm-3时，费米能级EFp＝0，即费米能级到达价带顶EV。

对于N型掺杂，当n0＝7×1018cm-3时，费米能级EFp＝0.664 eV，即费米能级到达L带底。进一步提高掺杂浓度，当n0＝9.5×1019cm-3时，费米能级EFp＝0.8eV，即费米能级达到Γ带底。这样，锗变为直接带隙材料。电子和空穴的辐射复合能量为费米能级EFp与价带顶EV的差值，即0.8 eV。

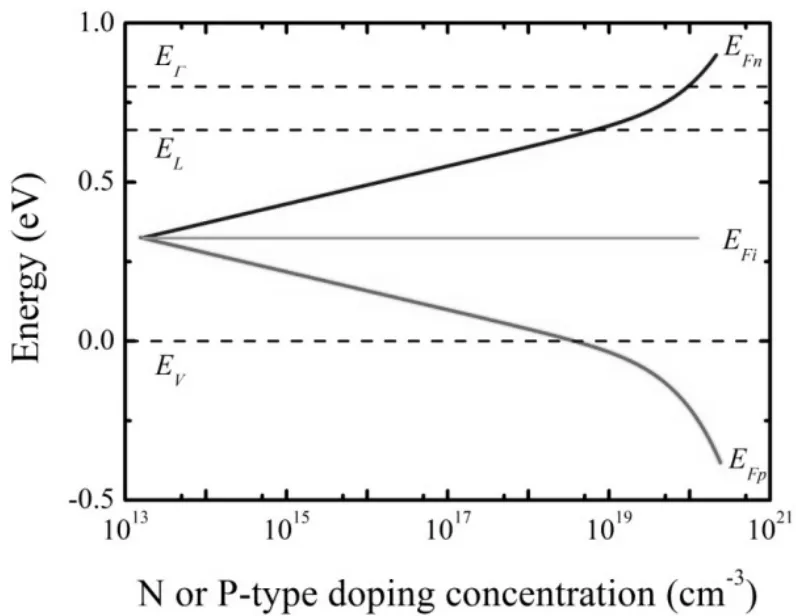
图4 体锗的费米能级与N型或P型掺杂浓度的关系Fig.4 Relationship between Fermi energy level of bulk Ge and N- or P-type doping concentration

图5 体锗的N型掺杂浓度与费米能级的关系Fig.5 Relationship between N- type doping concentration and Fermi energy level of bulk Ge

图5为L谷和Γ谷的电子浓度与费米能级的关系。由于Γ谷的能级较高，且态密度有效质量较小，Γ谷的电子浓度比L谷的小两个数量级。但是随着费米能级的升高，Γ谷的电子浓度迅速增加，当费米能级到达Γ带底时，Γ谷的电子浓度可达2.3×1017cm-3。N型掺杂使费米能级偏移，提高了Γ谷的电子浓度。

4 张应变和N型掺杂共同对锗能带的调节

从前文分析可知，单独张应变的调节作用，0.018的张应变可使锗的直接带隙变为0.53 eV。张应变是调节锗能带结构的一个有效方法。然而，采用张应变调节锗的能带结构存在两个挑战。第一，制备高质量、张应变大的锗材料比较困难。大的张应变可能带来高密度的晶体缺陷，粗糙的材料表面。通常在锗材料中引入张应变的方法是外延技术、应变转移和应变浓缩等技术。这些技术存在一定不足之处。第二、张应变将锗的带隙调节为0.53 eV，对应的辐射复合的发光波长为2.3μm，比通常的光通信、光电集成波长1.55μm的长，与实际需要有一些偏差。表明大的张应变不太符合材料制备和器件应用的要求。因此，需要适当降低张应变的大小。采用N型掺杂，当掺杂浓度为9.5×1019cm-3时，锗的费米能级到达导带的Γ带底，锗成为直接带隙材料。单独的N型掺杂也存在两个挑战。第一，在锗中高浓度的N型掺杂比较困难；第二，在高掺杂浓度下，自由载流子吸收比较严重，降低有效辐射复合的增益。因此，需要适当降低N型掺杂的浓度。

结合张应变和N型掺杂共同对锗能带结构的调节，可以解决上述挑战。为实现锗的直接带隙，计算了张应变和N型掺杂联合对锗能带结构的调节，结果如图6所示。可见，随着张应变的增加，N型掺杂浓度降低。几组典型的直接带隙锗材料的参数如下：张应变为0时，N型掺杂浓度为9.5×1019cm-3，对应辐射复合能量为0.8eV；张应变为0.005时，N型掺杂浓度为5.9×1019cm-3，对应辐射复合能量为0.73eV；张应变为0.010时，N型掺杂浓度为3.1×1019cm-3，对应辐射复合能量为0.65eV；张应变为0.015时，N型掺杂浓度为1.2×1019cm-3，对应辐射复合能量为0.57eV。张应变和N型掺杂的共同调节作用，缓解了对大张应变、高掺杂浓度的要求，更利于实际器件的制备。

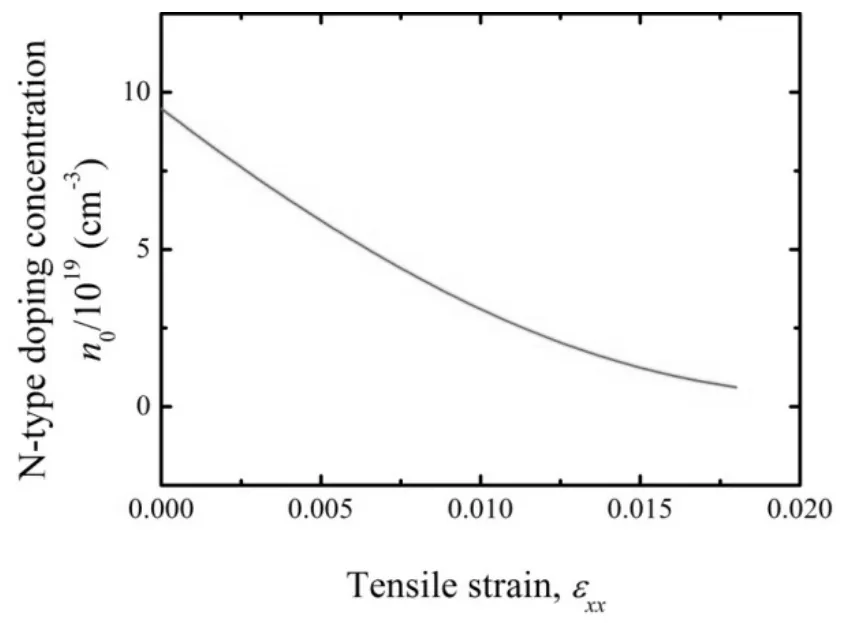
图6 N型掺杂浓度与张应变的关系Fig.6 Relationship between N-type doping concentration and tensile strain

5 结论

本文介绍了体锗的能带结构，从理论上计算分析了张应变和N型掺杂对锗能带结构的调节。张应变使价带和导带的能级分裂、偏移，N型掺杂使费米能级偏移。这样，增加电子在导带Γ谷的分布浓度，从而将锗变为准直接带隙的材料。单独张应变作用，当张应变为0.018时，锗的直接带隙为0.53eV。单独N型掺杂作用，掺杂浓度为9.5×1019 cm-3时，锗的费米能级到达导带的Γ带底。联合张应变和N型掺杂对锗能带结构的调节，既可以任意调整锗的能带结构（能级），又可缓解对大的张应变和高的掺杂浓度的要求，从而有利于发光材料的理论设计和实验制备。

[1]王兴军,苏昭棠,周治平.硅基光电子学的最新进展[J].中国科学: 物理学 力学 天文学,2015,45(1): 014201-1-31.Wang X,Su Z,Zhou Z.Recent progress of silicon photonics[J].SCIENTIA SINICA Physica,Mechanica & Astronomica,2015,45(1): 014201-1-31.(in Chinese)

[2]沈浩,李东升,杨德仁.硅基光源的研究进展[J].物理学报,2015,64 (20): 204208.Shen H,Li D,Yang D.Res earch progress of silicon light source[J].Acta P hys.Sin.,2015,64 (20): 204208.(in Chinese)

[3]Chen H,Verheyen P,Heyn P,et al.-1 V bias 67 GHz bandwidth Si-contacted germanium waveguide p-i-n photodetector for optical links at 56 Gbps and beyond[J].Opt.Express,2016,24(5): 4622-4631.

[4]Kuo Y,Lee Y,Ge Y,et al.Strong quantum-confined Stark effect in germanium quantum-well structures on silicon[J].Nature,2005,437: 1334-1336.

[5]Pillarisetty R.Academic and industry research progress in germanium nanodevices[J].Nature,2011,479: 324-328.

[6]Camacho-Aguilera R,Cai Y,Patel N,et al.An electrically pumped germanium laser[J].Opt.Express,2012,20(10):11316-11320.

[7]Physical properties of germanium[EB/OL].http://www.ioffe.ru/SVA/NSM/Semicond/Ge/

[8]Liu J,Cannon D,Wada K,et al.D eformation potential constants of biaxially tensile stressed Ge epitaxial films on Si(100)[J].Phys.Rev.B,2004,70(15): 155309.

[9]Neamen D.Semiconductor Physics and Devices[M].4th ed.,Newyork,The McGraw-Hill Companies,2011.

【责任编辑：高潮】

Adjusting Ge band structure through tensile strain and N-type doping

ZHOU Zhiwen1,GUO Haigen2,LI Shiguo1,SHEN Xiaoxia1,WANG Ying1
（1.School of Electronic Communication Technology,Shenzhen Institute of Information Technology,Shenzhen 518172,China;2.Office of Retirement work committee,Shenzhen Institute of Information Technology,Shenzhen 518172,China ）

Based on the band structure of bulk Ge,the adjustment of Ge band structure through tensile strain and N-type doping was theoretically calculated and analyzed.Valance bands and conduction bands were splitted and shifted due to the tensile strain.While,the Fermi energy level was moved by N-type doping.These adjust Ge into a pseudo direct band gap material.By introducing a tensile strain of 0.018 alone,the Ge band structure was changed to be direct with a direct band gap of 0.53 eV.With doping a N-type dopant concentration of 9.5×1019cm-3alone,Fermi energy level was shifted to the bottom of Γ band.It is beneficial to adjusting the Ge band structure and fabrication of these materials practically by introducing proper tens ile strain and N-type doping.The results provide reference to the des ign and fabrication of Ge-based light emitting devices.

Ge; tensile strain; N-type doping; band structure; light emitting device

TN304.1

A

1672-6332（2017）03-0059-05

2017-10-9

广东省高等学校优秀青年教师项目（Yq2014123）。

周志文（ 1982-），男（汉），湖北汉川人，副教授，博士，主要研究方向：半导体材料和器件。E-mail：zhouzw@sziit.com.cn