基于粒子群优化的三轴磁强计非线性误差校正*

宋忠国， 郑家欢， 张金生， 席晓莉

(1.西安理工大学 自动化与信息工程学院，陕西 西安 710048；2.西安工业大学 光电工程学院，陕西 西安 710048)

基于粒子群优化的三轴磁强计非线性误差校正*

宋忠国1， 郑家欢2， 张金生1， 席晓莉1

(1.西安理工大学自动化与信息工程学院，陕西西安710048；2.西安工业大学光电工程学院，陕西西安710048)

三轴磁强计的非线性误差是影响其测量精度的重要因素，而传统三轴磁强计误差模型仅考虑零偏、磁轴非正交和灵敏度误差，无法实现对磁测误差有效剥离和校正。通过对传统误差模型进行扩展，提出了三轴磁强计的非线性误差模型，并利用自适应粒子群优化(APSO)算法对非线性误差模型参数进行反演。实验结果表明：可以有效地补偿三轴磁强计的非线性测量误差，相较于传统校正方法，在误差参数规模较大情况下，APSO算法具有更好的全局搜索能力，可大幅提高误差参数反演精度及算法收敛速度。

三轴磁强计； 误差校正； 自适应粒子群优化算法； 参数估计

0 引 言

三轴磁强计作为一种低功耗、轻小型磁矢量场采集装置，广泛应用于飞行器定向、自主导航/定轨、生物工程、勘探等领域。而在工程应用中[1～3]，受传感器加工工艺限制和测量环境磁场扰动的影响，磁强计测量输出误差较大，实际应用中应进行严格校正。

传统三轴磁强计校正中使用的误差模型主要考虑了零偏、灵敏度误差、三轴非正交误差等线性误差因素。针对该类误差模型，文献[4～7]中通过采集磁强计不同方位的测量数据，利用最小二乘或最大似然估计模型中误差参数。而上述方法中均未对非线性误差进行校正。相关研究表明：国内外众多高精度磁通门或磁阻式三轴磁强计会敏感到磁轴正交方向的磁场，即横轴效应(transverse field effect,TFE)，从而使输出磁场对外呈现非线性[8]。此外，磁滞亦是磁强计产生非线性误差的重要因素。

本文通过建立三轴磁强计的非线性误差模型，对扩展误差参数利用智能优化算法对线性及非线性误差参数进行协同估计，实现了对三轴磁强计高精度校正，通过仿真和实验结果验证了该方法的有效性。

1 磁强计非线性误差模型

定义三轴磁强计磁轴所处非正交坐标系(x,y,z)和标准正交系(i,j,k)。令z与k重合，j位于xOy平面并与k垂直，i垂直于yOz平面,两坐标系之间关系为

(1)

式中α,β,γ为两坐标系之间的欧拉角。

定义磁强计零偏Bb和灵敏度误差Cs为

Cs=diag(Csx,Csy,Csz)T,Bb=[BbxBbyBbz]T

(2)

三轴磁强计线性误差模型为

B=CsCE(BM-Bb)

(3)

式中BM=[BMx,BMy,BMz]T为三轴测量磁矢量，B=[Bx,By,Bz]T为真实磁场矢量。对式(3)取模得到

‖B‖=‖CsCE(BM-Bb)‖=‖KBM-b‖

(4)

式中 上三角矩阵K为等效乘性误差；b=CsCEBb为等效加性误差。

考虑非线性误差为乘性误差，因此,将矩阵K中的元素进行扩维，本文采用4阶多项式替代原线性模型中的误差参数k1～k6，表示为

(5)

在相同背景磁场下测量N组三轴磁强计在不同指向下输出磁场矢量，令其模值与已知外加总磁场强度H0(利用质子、光泵等高精度标量磁测装置获取)之间均方根误差最小，即可完成对非线性误差参数的估计，即将误差参数反演问题转化为最优参数估计问题

(6)

获取误差参数估计量后利用式(4)即可完成对磁强计输出数据进行校正。

上述模型基于对误差参数进行扩维达到提高磁强计线性及非线性误差剥离的目的，所估计误差参数的增加将直接导致计算量增加及算法收敛性能变差，且所需观测数据量增大，对于4阶非线性模型，待估非线性参数为24个，最低需27组不同方位下的观测数据。因此，采用全局优化性能好的智能优化算法可有效提升误差参数估计的准确性。

2 基于自适应粒子群优化的磁强计校正算法

粒子群优化(particle swarm optimization,PSO)算法是一种基于种群进化的智能优化技术，算法中的每个粒子表示一个搜寻解空间，该算法对初值敏感且具有极快的收敛速度，使之极易落入局部最优值。

本文采用一种改进的自适应粒子群优化(adaptive PSO,APSO)算法，可在不影响收敛速度的前提下提高算法全局最优搜索性能。

PSO算法流程简述如下：假定D维搜索空间中，种群粒子数为m，对于第k次迭代，粒子i,i=1,2,…,m的位置(取值)和变异速度为

(7)

粒子i的最优取值为

Pi(k)=(pi1(k),pi2(k),…,piD(k))

(8)

最优种群为

Gi(k)=(gi1(k),gi2(k),…,giD(K))

(9)

粒子调整速度和位置为

vij(k+1)=w·vij(k)+c1·rand(0,1)·(pij(k)-xij(k))+

c2·rand(0,1)·(gij(k)-xij(k))

(10)

xij(k+1)=xij(k)+vij(k+1)

(11)

式中j=1,2,…,D为粒子维数；w为调整权重；c1,c2为学习因子。通过迭代寻找最优解，进而通过适应度来评价解的品质。

APSO算法主要从以下方面进行改进：

1)种群间共享适应度优于自身解信息，使得适应度好的种群引导其他种群提高其适应度。由于在进化过程中不仅仅考虑全局最优信息，因此，落入局部最优解的概率大幅降低。

2)改进算法利用适应度对种群进行排序(rank)，通过适应度来调整种群进化速率。种群更新速率方程表示为

(puj(k)-xij(k))

(12)

式中u为适应度优于i的粒子个体；umax为个体u的最大个数。

此外，权重w通常设置为常值，为提高收敛性及收敛后解的精度，本文将权重w设计为线性递减

(13)

式中wmax和wmin分别为w的上下边界；kmax为最大迭代次数。

3 实验验证

搭建实验系统，将待测三轴磁强计及数据采集处理前端固联于无磁转台，并置于三轴赫姆霍兹线圈中心处；利用赫姆霍兹线圈产生恒定指向磁场，将质子磁力仪探头靠近待校正三轴磁强计，用于监测所模拟磁环境的准确场强；整个实验系统内置于无磁实验环境中，以避免外部随机磁扰及噪声的影响,如图1所示。

图1 三轴磁强计校正实验系统

通过旋转无磁转台得到多组不同方位下三轴磁强计输出的量测数据，如图2所示为参考磁场约40 000 nT时采集的实验数据。利用磁强计输出磁矢量数据集和总场监测数据即可实现对非线性误差模型参数反演。

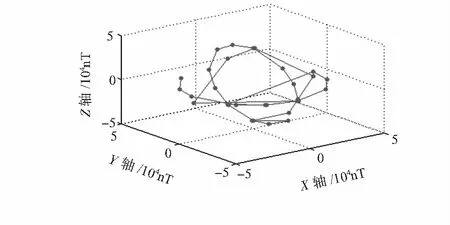
图2 三轴磁强计校正实验数据

图3所示为基于27组参数非线性误差模型，利用APSO反演得到非线性误差系数，并对三轴磁强计进行校正后所得结果，通过与文献[4～7]中的基于9参数线性误差模型并采用最小二乘法校正结果进行对比，表明：采用前者方法校正后，三轴磁强计输出场量更稳定；表1为校正后输出结果与质子磁力仪监测场强对比结果，表明：采用非线性校正方法得到磁强计输出绝对偏差及相对偏差均优于传统线性方法。

图3 三轴磁强计校正结果曲线

4 结 论

针对三轴磁强计非线性误差校正问题，从误差模型及模型参数估计算法入手，建立了三轴磁强计的非线性误差模型，利用APSO算法对多维误差参数进行估计。实验表明:方法可有效提高三轴磁强计的校正精度，对于中等精度的三轴磁强计，校正后平均测量偏差低于1 nT。该方法简单易行，便于工程应用。本文方法及实验仅针对磁强计所处静态环境有效，搭载至运动载体进行实时校正时，受磁强计本身动态特性影响，数据动态测量误差将导致非线性校正算法对多维数据估计收敛困难。

[1] Sheinker Arie, Frumkis Lev,Ginzburg Boris,et al. Magnetic anomaly detection using a three-axis magnetometer[J].IEEE Transactions on Magnetics,2009,45(1):160-167.

[2] Birsan Marius.Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer[J].IEEE Transactions on Magnetics,2011,47(2):409-415.

[3] Foster C C,Elkaim G H.Extension of a two-step calibration methodology to include nonorthogonal sensor axes[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(3):1070-1078.

[4] Valérie Renaudin,Muhammad Haris Afzal,Gérard Lachapelle.Complete tri-axis magnetometer calibration in the magnetic domain[J].Journal of Sensors,2010,2010:1-10.

[5] Vasconcelos J F,Elkaim G,Silvestre C,et al.Geometric approach to strapdown magnetometer calibration in sensor frame[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):1293-1306.

[6] Pang Hongfeng,Chen Dixiang,Pan Mengchun,et al.A new calibration method of three axis magnetometer with nonlinearity suppression[J].IEEE Transactions on Magnetics,2013,49(9):5011-5015.

[7] Brauer P,Merayo J M G,Nielsen O V,et al.Transverse field effect in fluxgate sensors[J].Sensors and Actuators A:Physical,1997,59(1):70-74.

[8] Hossen Md Sakhawat,Rabbi Fazle,Rahman Md Mainur.Adaptive particle swarm optimization(APSO) for multimodal function optimization[J].International Journal of Engineering and Technology,2009,1(3):98-103.

Nonlinearerrorcalibrationofthree-axismagnetometerbasedonPSOalgorithm*

SONG Zhong-guo1， ZHENG Jia-huan2， ZHANG Jin-sheng1， XI Xiao-li1

(1.FacultyofAutomationandInformationEngineering,Xi’anUniversityofTechnology，Xi’an710048，China;2.SchoolofOpto-ElectronicEngineering,Xi’anTechnologicalUniversity，Xi’an710048，China)

The nonlinear error of three-axis magnetometer is an important factor affecting its measurement precision, and the traditional error model for three-axis magnetometer only considering zero bias, axis nonorthogonal and sensitivity error, unable to realize the effective apartment and calibration of magneto measurement errors.By extending traditional error model, propose nonlinear error model for three-axis magnetometer.Adaptive particle swarm optimization (APSO) algorithm is used for nonlinear error model parameters inversion.Experimental results show that the proposed method can effectively compensate the unlinear measuring error of three-axis magnetometer, and under the condition of larger scale of error parameters, APSO has better global search ability compared with the traditional calibration methods, which can significantly improve error parameter inversion precision and the convergence speed of algorithm.

three-axis magnetometer; error calibration; adaptive particle swarm optimization(APSO) algorithm; parameter estimation

10.13873/J.1000—9787(2017)12—0040—03

TP 212.1

A

1000—9787(2017)12—0040—03

2017—10—18

国家高技术研究发展计划(863计划)资助项目(2015AA7026084)

宋忠国(1982-)，男，博士，讲师，主要从事地磁匹配制导及地磁定轨相关方面研究工作，E—mail:songzhongguo@xaut.edu.cn。