高墩大跨刚构桥桥墩的稳定性与承载能力研究

彭容新，陈爱军

(中南林业科技大学 土木工程学院，长沙 410004)

高墩大跨刚构桥桥墩的稳定性与承载能力研究

彭容新，陈爱军＊

(中南林业科技大学 土木工程学院，长沙 410004)

以张家界太极溪特大桥为研究对象，同时使用ANSYS与ABAQUS两种有限元软件进行计算分析,首先，采用线弹性稳定分析方法对大跨预应力混凝土连续刚构桥各施工阶段双肢薄壁墩的稳定性和失稳模态进行计算；随后，使用非线性仿真分析方法对该桥各施工阶段进行计入初始几何缺陷的非线性分析.通过分析可知：在相同的荷载工况作用下，各施工阶段的极限承载力均小于成桥阶段的极限承载能力；裸墩状态与0号块施工阶段该桥桥墩的纵向稳定性较小，结构在几何缺陷与材料塑性的影响下，承担荷载能力明显减弱.利用ANSYS与ABAQUS两种软件计算所得结论极为相近，通过其结果的相互验证，可以在一定程度上确定本次计算分析所建模型与分析方法的正确性，可为今后该类桥桥墩的施工、设计与研究提供参考.

张家界太极溪特大桥；大跨连续刚构桥；非线性分析；稳定性；极限承载能力；双肢薄壁高墩

近年来，随着全国经济的不断发展，特别是在“十三五”规划中提出了关于乡乡通公路的新发展目标，这使得乡乡公路与城乡公路以前所未有的速度向山区延伸.但在进行山区公路规划时，无法避免的会存在沟深或山高等特殊地形状况，这就致使高墩大跨预应力混凝土连续刚构桥这种桥型备受青睐.由于该类桥桥墩尤其是高桥墩作为轴向受力构件，自身柔度大，故其极限承载力与稳定性问题受到广泛关注.而在以往对于双肢薄壁墩的分析大多是进行线弹性屈曲稳定分析，这种计算方法能够初步估计得到相应的极限承载力，但无法得到计入初始缺陷而引起的几何变形和材料塑性变形对极限承载能力的影响.故而在本次分析中，以张家界太极溪特大桥为例，利用ANSYS中的具有大变形功能的单元，同时计入成桥阶段的位移与材料本构关系，对该桥桥墩进行非线性稳定分析.竖直双肢薄壁墩可以增加桥墩纵桥向竖向荷载作用下的刚度，同时其水平抗推刚度小，在桥梁纵向允许的变位大，这不仅可以减小主梁附加内力，而且由于主梁的负弯矩峰值出现在双肢墩的墩顶，且较单壁墩小一些，故可减小主梁在墩顶截面处尺寸，增加桥梁美感[1].特别是对于山区中的高桥墩，其柔度必须适应混凝土收缩、徐变，温度效应，风荷载与汽车荷载所产生的水平位移，并减小桥墩与主梁固结所产生的次应力.故而对双肢薄壁墩的稳定性与承载能力计算，尤其是进行各方向荷载作用下桥墩承载能力的分析，可对今后同类型桥梁的设计、施工与研究提供相应的参考.

1 高墩大跨连续刚构桥有限元计算

1.1 桥梁概况

本文以张家界太极溪特大桥为研究对象，该桥由于地形的特殊情况，设计采用大跨预应力混凝土连续刚构桥.桥梁全长252 m，跨径组成为66 m +120 m +66 m；主梁截面采用单箱单室，采用对称悬臂施工的施工工艺；桥墩采用双肢薄壁墩，截面为空心薄壁墩，双肢间无横撑相连，其中桥墩最高为57.06 m.

1.2 有限元计算模型

本次采用ANSYS大型通用有限元分析软件建立张家界太极溪特大桥的空间有限元模型，见图1.其中主梁、主墩与承台采用实体单元Solid 65模拟.Solid 65单元是一个高阶3维8节点固体结构单元，单元具有拉裂与压碎的性能，可用于模拟混凝土的开裂、压碎及塑性变形.

同时，分别建立该桥裸墩、0号块与最大悬臂施工阶段的有限元模型(如图 2所示)进行桥墩的线弹性稳定性分析与非线性稳定分析.

在进行线弹性屈曲分析时，各施工阶段均采用荷载工况：一期恒载+风荷载+温度荷载.对于风荷载，根据公路桥涵设计通用规范第4.3.8条[2]，横向风压W=K1·K2·K3·K4·W0.其中W0为基本风压，根据桥墩所在地的风速，取基本风压为209.31 Pa；K1为设计风速频率换算系数，取1.00；K2为风载体型系数，取0.9；K3为风压高度变化系数，取 1.37；K4为地形、地理条件系数，取1.3；纵向风压为横向风压的0.7乘以桥墩迎风面面积.

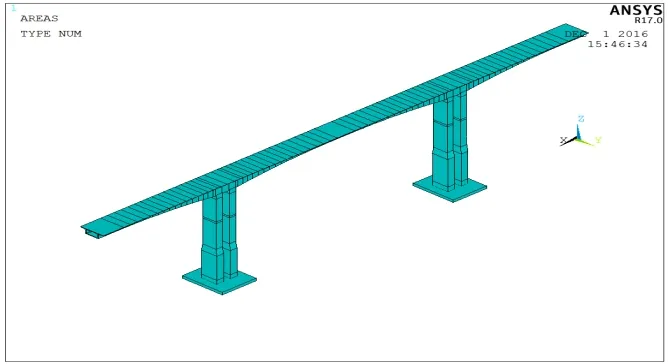
图1 有限元计算模型

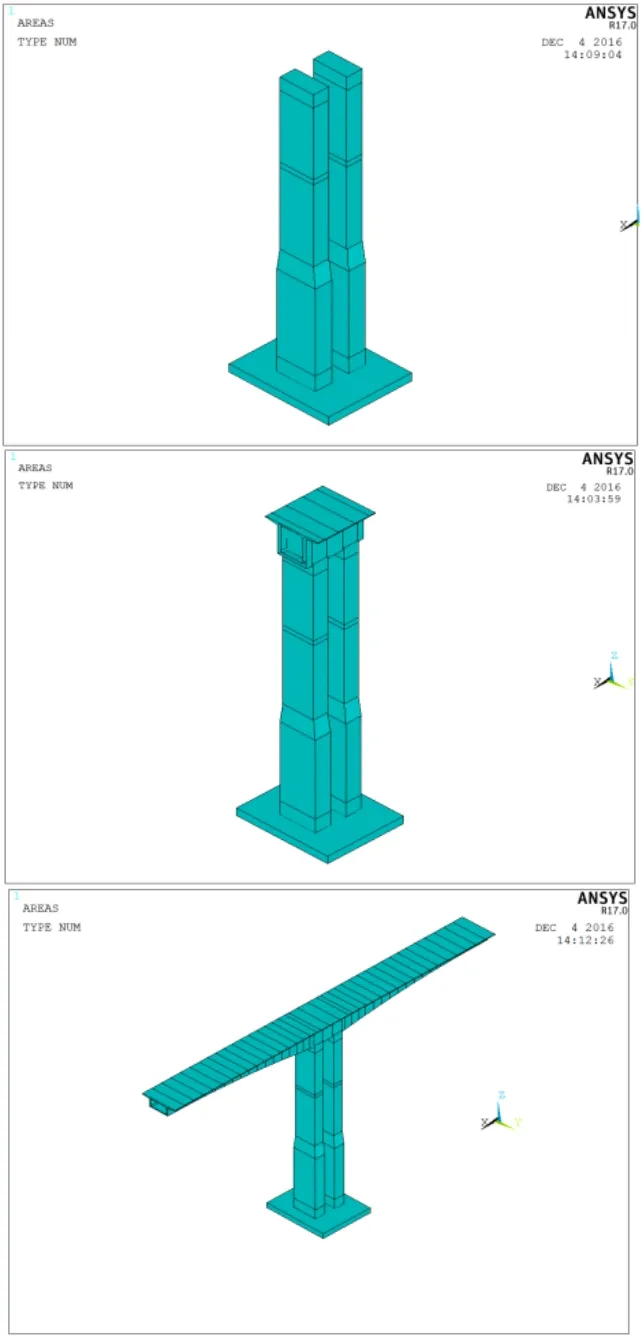
图2 大桥各施工阶段有限元计算模型

1.3 稳定分析计算方法

在分析线弹性稳定问题时常用的方法有静力平衡法(Eular方法)、能量法(Timoshenko方法)、缺陷法和振动法.在解决复杂的稳定性问题中，大量使用的是稳定问题的近似求解方法，其中基于能量变分原理的近似法为最常用的计算方法，如Ritz法，有限元方法可以看成是Ritz法的特殊形式.

非线性稳定性[3-7]分析采用逐步施加荷载增量来求得结构失稳时的临界荷载.增量施加过程中，应力及结构变形不断增加，单元刚度不断减小.几何刚度矩阵对总刚度的削弱作用不断增强，当荷载增大到某一数值时，总刚度矩阵[K]出现非正定，即结构失稳.采用U. L 列式法建立结构的非线性平衡方程可表示为：其中为小变形弹塑性刚度矩阵；为几何刚度矩阵；为大变形弹塑性刚度矩阵.

1.4 钢筋混凝土材料本构关系

桥梁结构在受超载作用时会产生塑性变形，故在进行极限承载能力分析时，需考虑材料塑性区域的非线性特性，其中混凝土材料采用Ottosen非线弹性本构模型，其受力损伤与应变-应变关系如图3所示.而钢筋则采用理想弹塑性模型的本构关系，令其为各项同性材料，可得本构方程为

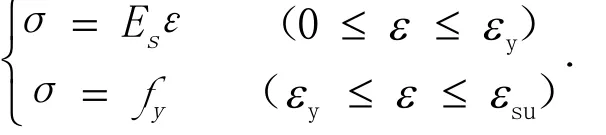
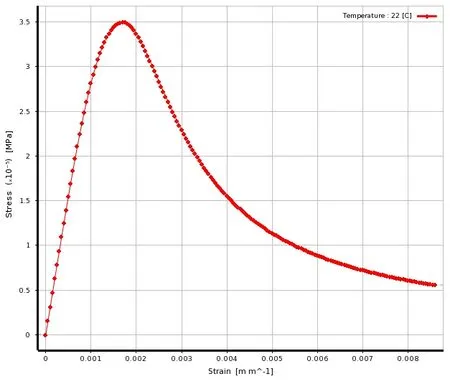
图3 混凝土受力损伤与应变-应变关系

2 非线性分析计算结果

2.1 各施工阶段的线弹性屈曲分析

在进行极限承载力计算前，首先对该桥各施工阶段进行线弹性屈曲分析，从而初步评估双肢薄壁墩及全桥的稳定性与极限承载能力[8-9]，其中该桥各施工阶段稳定系数如表1所示，各施工阶段的第一阶失稳形态如图4所示.由表1的稳定系数可知，0号块施工阶段为最有利于双肢薄壁墩受力的施工阶段，其稳定系数为成桥阶段稳定系数的 1.8倍；而最大悬臂状态为最不利状态，其稳定系数为全桥稳定系数的93.17%.故而对双肢薄壁墩、0号块施工阶段与最大悬臂状态进行相应的非线性与承载能力计算，对于该类桥在各个施工阶段桥墩的稳定性，与全桥运营阶段的承载能力的提高都有着非同一般的指导意义.

表1 各施工阶段屈曲稳定系数

通过线弹性屈曲分析可以初步看出，该桥各施工阶段为最不利荷载作用下的第1阶稳定系数均大于51.957，满足构件稳定系数大于4～5的要求[10-11].同时，由各施工阶段第一阶失稳形态可以看出，该桥桥墩结构纵桥向变形大于横向变形，即桥墩横桥向稳定性大于顺桥向稳定性，此规律满足双肢薄壁墩顺桥向刚度大于横桥向的基本力学特性.

图4 施工阶段第一阶失稳形态

2.2 双肢薄壁墩的非线性分析

在对于该桥双肢薄壁墩进行非线性分析时，将结构弹性失稳系数的10%变形作为结构初始缺陷计入非线性分析，采用屈曲稳定系数的 1.2倍作为荷载加大的倍数，运用逐步加载的方式对桥墩的极限荷载进行求解.

图5给出了双肢薄壁墩在竖向荷载作用下未计入几何缺陷与计入几何缺陷几何非线性与几何、材料双重非线性的荷载-位移曲线.其中计入几何缺陷的几何非线性失稳变形如图6所示.由图5可以看出，几何缺陷与材料弹塑性特性对于该桥桥墩的承载力计算有着显著的影响.由失稳变形亦可看出，结构在几何缺陷的影响下，双肢薄壁墩向一侧发生明显偏移，致使该桥墩提前进入屈曲状态，而在计入材料塑性时，结构承担荷载能力减弱更加显著.

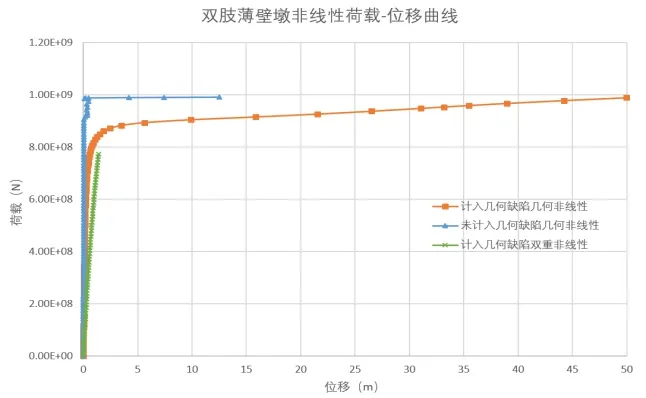
图5 双肢薄壁墩非线性荷载-位移曲线

图6 极限荷载作用下双肢薄壁墩的变形云图

2.3 0号块施工阶段的非线性分析

按公路钢筋混凝土及预应力钢及混凝土桥涵设计规范[12]进行结构承载能力极限状态计算时，荷载增大系数为1.2，混凝土与钢筋材料的安全系数为1.25，结构工作条件系数为0.95，得到该桥结构稳定安全系数为：其中稳定安全系数为某一计算极限荷载与对应结构实际荷载的比值.

在进行成桥阶段计算时，计入支座沉降、恒载、钢束预应力荷载、钢筋混凝土收缩徐变与偏载时可得墩顶最大荷载：1.72×108N，从而得到各施工阶段的稳定安全系数如表2所示.其中各施工阶段稳定安全系数皆大于2.507，符合稳定安全系数的基本要求.并从表2中可以看出，该桥于0号块施工阶段得到桥墩最小极限荷载为4.35×108N，稳定安全系数为所有施工阶段的最小值，故对该桥桥墩进行极限承载能力的研究.

图 7给出了荷载作用下非线性荷载-位移曲线，图8为三向极限荷载作用下桥墩变形云图.

表2 各施工阶段稳定安全系数

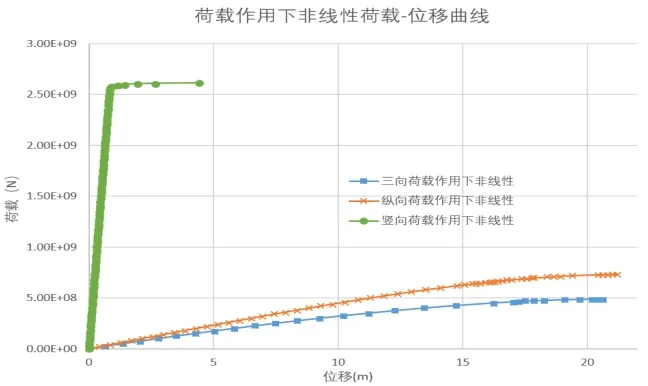
图7 荷载作用下非线性荷载-位移曲线

由非线性分析结果可得，在纵向荷载作用下，该桥墩结构的极限承载力为 6.29×108N，其变形云图见图 9；在竖向荷载作用下，该桥墩结构的极限承载力为2.52×109N，其变形云图见图10.

图8 三向极限荷载作用下桥墩变形云图

图9 纵向极限荷载作用下桥墩变形云图

通过比较图8、图9与图10的变形云图可知，纵向荷载对于该桥桥墩的承载能力有着显著的影响，特别是对于该类无中横撑的双肢薄壁墩，没有横撑的协调受力使得结构极易发生侧移失稳.但由于0号块施工阶段上部结构较小，对该桥桥墩稳定性的影响较小，故在对失稳形态进行分析时，并未发现面外失稳.

图10 竖向极限荷载作用下桥墩变形云图

2.4 最大悬臂状态的非线性分析

在各施工阶段中，由于悬臂梁梁体的不均匀自重、单边日照引起的温度效应、挂篮荷载作用以及横桥向与纵桥向的风荷载使得最大悬臂状态为最关键施工阶段，故对其进行非线性分析对各施工阶段与成桥极限承载能力的评估有着深刻的指导意义.通过计算分析可得三向荷载作用下非线性荷载-位移曲线如图 11所示，其极限荷载作用下的失稳模态如图12所示.

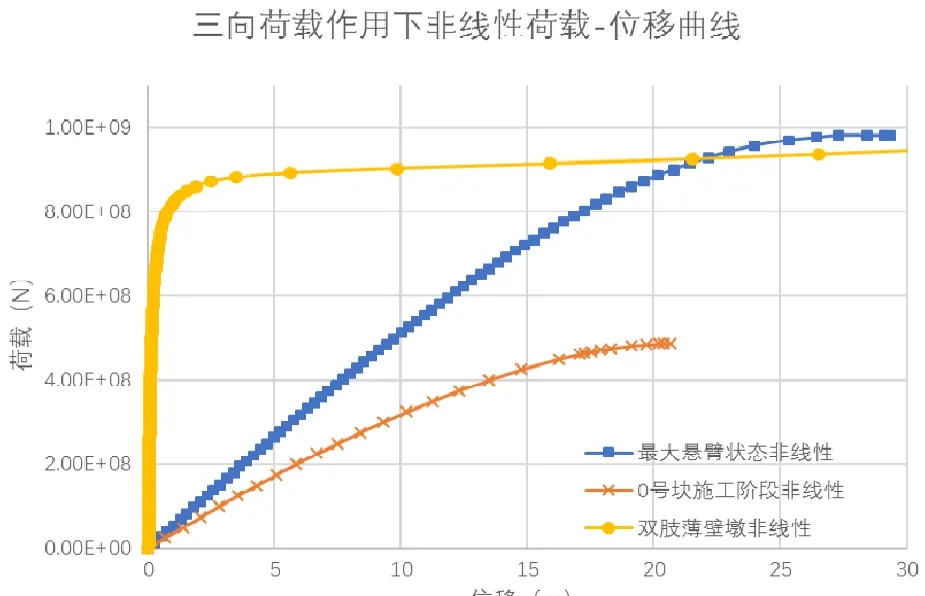
图11 三向荷载作用下非线性荷载-位移曲线

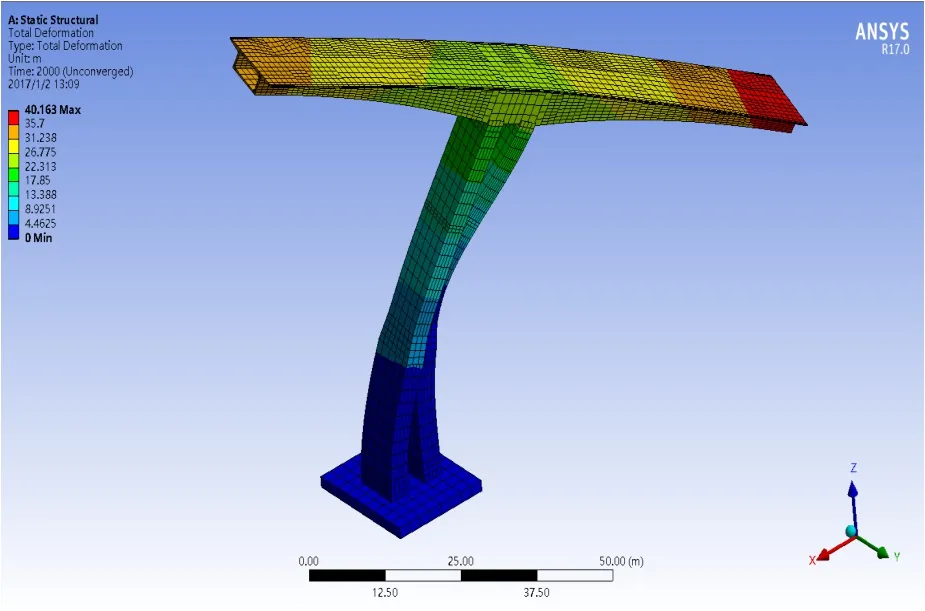
图12 三向极限荷载作用下桥墩变形云图

由图11可知，最大悬臂状态的极限承载力为7.21×108N，其相比裸墩状态减小 10.95%，而相对0号块施工阶段提高65.75%，且对于稳定安全系数亦有非常显著地影响.由图12可知，在极限荷载作用下该桥桥墩有着横向失稳引起的侧向扭转变形.然而正是因为桥墩横向刚度辅助该施工阶段承受荷载作用，使得其相较0号块施工阶段稳定性大大提高.通过比较0号块与最大悬臂失稳形态可知，在三向荷载作用下，0号块施工阶段结构易发生面内失稳，而在上部悬臂结构施工完成后，其结构在三向荷载作用下易发生横向面外扭转失稳.

同时，比较图5、图7与图11中各施工阶段的非线性荷载-位移曲线可知，在计入纵向与横向荷载时，曲线相对仅存在竖向荷载作用时的曲线在极限位置转折更加平缓，故而竖向刚度对于悬臂施工阶段的稳定性有着至关重要的影响.

3 ANSYS与ABAQUS两种软件非线性分析结果的探讨

3.1 ABAQUS建立有限元计算模型

本次同时采用有限元软件ABAQUS建立张家界太极溪特大桥的有限元模型.ABAQUS为大型通用有限元计算软件，其求解器计算非线性收敛速度较快，并更加容易操作和使用，故在求解非线性问题时具有非常明显的优势.

在有限元建模时，其主梁、主墩与承台采用八节点实体单元 C3D8R对该结构进行仿真分析.其中该桥0号块施工阶段有限元模型如图13所示.

图13 有限元计算模型

3.2 0号块施工阶段非线性分析计算结果比较

利用ABAQUS对0号块施工阶段结构进行竖向与三向荷载作用下的非线性分析，得到非线性荷载-位移曲线如图14所示，其三向极限荷载作用下的变形云图如图15所示.

通过比较ANSYS与ABAQUS的非线性荷载-位移曲线可知，竖向荷载与三向荷载的非线性曲线有着相同的形态与趋势，且 ABAQUS分析得到的竖向极限荷载为 2.37×109N；三向极限荷载为3.25×108N.其中竖向极限荷载为ANSYS计算结果的93.95%；三向极限荷载为ANSYS计算结果的74.63%.所得计算结果在有限元模型计算误差范围之内，证明了有限元计算模型的正确性.

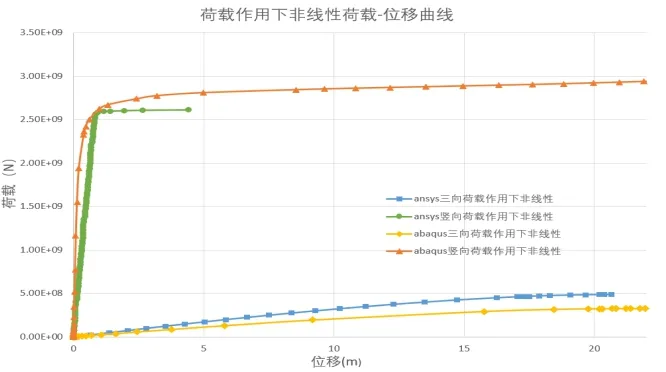
图14 荷载作用下非线性荷载-位移曲线

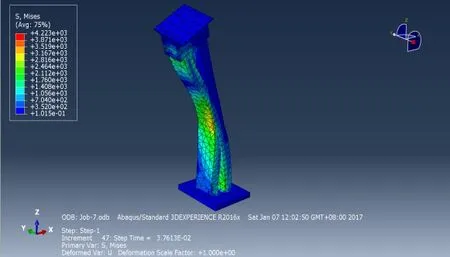
图15 三向极限荷载作用下桥墩变形云图

通过比较ANSYS与ABAQUS极限荷载作用下桥墩的变形云图可得，在三向荷载作用下，无论是ANSYS还是ABAQUS，其变形形态皆为面内失稳引起的该桥桥墩纵向扭转，这致使双肢逐步靠近并最终到达极限受力状态.由此可见，对于双肢薄壁墩，如在双肢间添加横撑，此横撑定会对0号块施工阶段的该桥桥墩的稳定性有着较大的提升，同时该桥桥墩的极限承载能力也有着显著的提高.并且由失稳模态的比较可进一步证明本次分析所使用的有限元计算模型的正确性.

4 结论

通过以上高墩大跨连续刚构桥桥墩的非线性分析，得出如下结论：

(1)经过对该桥各施工阶段的线弹性屈曲分析可知，该桥桥墩各施工阶段屈曲系数均大于51.957，且在相同的荷载工况作用下施工阶段的极限承载力要小于成桥阶段的极限承载能力.特别是对于悬臂施工阶段，在温度荷载和风荷载作用下，其屈曲稳定系数要远小于裸墩状态与0号块施工阶段的屈曲系数.

(2)通过比较0号块与最大悬臂失稳形态可知，在三向荷载作用下，0号块施工阶段结构易发生面内失稳，而在上部悬臂结构施工完成后，其结构在三向荷载作用下易发生横向面外扭转失稳.

(3)通过各施工阶段的非线性分析，在计入支座沉降、恒载、钢束预应力荷载、钢筋混凝土收缩徐变与偏载时，各施工阶段的稳定安全系数均大于1.58.其中裸墩状态的极限承载力最大，其稳定安全系数亦为各施工阶段的最大值.

(4)对该桥各施工阶段的非线性荷载-位移曲线的分析可知，在计入纵向与横向荷载时，曲线相对仅存在竖向荷载作用时的曲线在极限位置转折更加平缓，说明该桥桥墩的竖向刚度对于结构的稳定性有着至关重要的影响.

(5)通过比较ANSYS与ABAQUS的非线性荷载-位移曲线与桥墩变形云图可知，本次分析建立的有限元计算模型较为合理.相比 ABAQUS，ANSYS虽计算时收敛速度较慢，计算过程更为复杂，但其计算结果更为精确，特别是对于计入材料非线性与几何缺陷时，ANSYS能够更为真实的反应该桥桥墩的非线性特性与极限承载能力.

[1]邵旭东. 桥梁工程[M]. 第2版. 北京: 人民交通出版社, 2004.

[2]JTG D60-2015, 公路桥涵设计通用规范[S].

[3]刘进. 高墩大跨刚构桥桥墩静力非线性与稳定性研究[D]. 长沙: 湖南大学, 2005.

[4]田志杰. 超宽圆端形薄壁空心桥墩稳定性研究[D]. 兰州: 兰州交通大学, 2013.

[5]刘恩. 桩柱式高桥墩桩基稳定性分析与室内模型试验研究[D].长沙: 湖南大学, 2007.

[6]曹文贵, 欧阳心和, 张永杰, 等. 基于能量法的桩柱式高桥墩—桩基结构稳定性分析[J]. 公路工程, 2007(05): 29-33; 44.

[7]冯鑫. 横向冲击作用下高桥墩的非线性动力稳定性分析[D].长沙: 湖南大学, 2011.

[8]赵明华, 刘恩, 汪优. 桩柱式高桥墩桩基稳定性分析[J]. 公路交通科技, 2008(07): 95-99.

[9]汪优. 高桥墩桩基稳定性分析及其优化设计研究[D]. 长沙:湖南大学, 2007.

[10]赵延安, 罗小峰, 刘海彬, 等. 桥墩结构形式对小花沟连续刚构桥高墩稳定性影响分析[J]. 公路, 2011(11): 65-69.

[11]陈立平, 马越峰, 朱刚, 等. 山区高速公路桥梁高桥墩压杆稳定性设计分析[J]. 公路交通科技, 2006(12): 107-109.

[12]JTG D62-2012, 公路钢筋混凝土及预应力钢及混凝土桥涵设计规范[S].

(责任编校：陈健琼)

Stability and Carrying Capacity of Long-Span Continuous Rigid Frame Bridge with High Piers

PENG Rongxin, CHEN Aijun＊
(School of Civil Engineering, Central South University of Forestry and Technology, Changsha, Hunan 413000, China)

Tai Ji River Bridge in Zhangjiajie is taken as the research object, and two kinds of the finite element software ANSYS and ABAQUS are used to calculate, and to analyze. Firstly, the stability and instability modes of the thin-walled piers of the long-span pre-stressed concrete continuous rigid frame bridge are calculated by the linear elastic stability analysis method. Then, the nonlinear simulation analysis method is used to analyze the nonlinear analysis of the initial geometric imperfections of the bridge. It can be seen from the analysis that under the same load condition, the ultimate bearing capacity of each bridge stage is less than the ultimate bearing capacity of the bridge stage. The longitudinal stability of the bridge pier is small. And under the influence of geometric defects and plasticity of materials, the load capacity of the structure is obviously weakened. The results obtained by ANSYS and ABAQUS are very similar. By the mutual verification of the results, we can determine the model and the model. The correctness of the analysis method can provide reference or basis for the construction, design and research of bridge piers in the future.

Zhangjiajie Tai Ji River Bridge; high pier and long span continuous rigid frame bridge;nonlinear analysis; stability; ultimate bearing capacity; double pier and thin wall high pier

U443.22

A

10.3969/j.issn.1672-7304.2017.05.0003

1672–7304(2017)05–0012–06

2017-08-03

国家自然科学基金项目(51178473)；湖南省“土木工程”重点学科资助项目(2013ZDXK002)

彭容新(1994-)，男，湖南长沙人，硕士研究生，主要从事桥梁新结构形式研究.E-mail: 1040801530@qq.com.＊

陈爱军(1973-)，男，湖南邵阳人，副教授，博士研究生，主要从事桥梁新结构形式研究.E-mail: 992357035@qq.com