把握函数本质 理解概念特征
2017-12-07黄元宋
黄元宋

【摘要】“变量与函数”是沪科版八年级上册的重要教学内容。本文论述教师要遵循科学的探究理念,把握函数概念的本质,合理运用正、反实例,让学生体验概念的探究过程,准确理解函数特征,培养学生观察分析、抽象概括的能力。
【关键词】《变量与函数》 概念教学 对应 反例 特征
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2017)09A-0065-02
函数概念是数学的基本概念之一,对数学的发展起着十分重要的作用。初中阶段的函数概念是从动态变化和联系对应的角度来进行定义的,该定义是对一个变化过程中两个量的描述。由于函数的特征是变化发展的,加上学生的知识储备不足,導致了学生对函数概念的理解有困难。因此,在课堂教学中教师要结合实例,帮助学生完成思维的飞跃。
一、抓住函数本质,突出“变化”与“对应”思想
从函数概念的本源来看,函数的起源来自于对事物运动、变化的分析,它描述了客观事物之间存在的动态变化而又互相依存的特殊关系,正是这种关系的存在,使得处于变化中的两个变量相互制约、相互牵制。因此,“变化”是函数的本质属性,也是函数教学的关键点,教师应以函数“变化”作为突破口展开教学。
在“变量与函数”教学问题提出的初始阶段,教师可以设计如下问题:
一辆汽车以每小时60千米的速度匀速行驶,行驶的里程为s千米,时间为t小时,首先填写下表,然后尝试用含有t的式子表示s。
学生在面对上述问题中s=60t时,对于给定的t值,也可以计算出对应的s值,但大多数学生仅是将其作为一个个独立的算式,没有从整体上进行联系,更不能深刻体会该过程中变量s随着变量t的变化而变化。因此,教师要设计一些典型的例子,计算由自变量得到相应的函数值,让学生在观察、比较、分析具体问题中量与量之间的变化关系。对于静止的表达式或表格,要引导学生将其看作是动态的过程,让学生从静止的关系中逐步过渡到量与量之间的动态关系上,实现静态到动态的飞跃。
另外,函数的本质也存在一一对应的关系。在学习函数之前,教材已经渗透了“对应”的思想,例如有理数与数轴上点的对应,因此在教学函数概念时,教师要通过实例让学生感受“对应”思想,通过非概念的变式使学生明晰“对应”是“唯一”确定的对应。
例如在概念探索阶段可以出示如下问题:
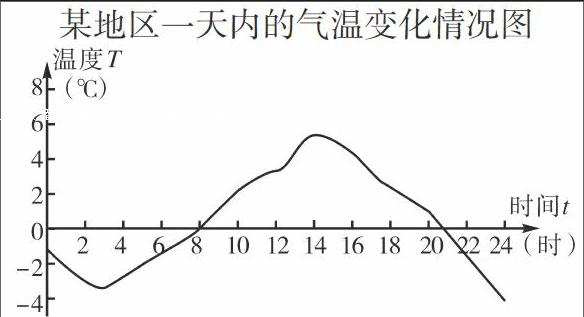
某地区一天内的气温变化情况图
(1)图象中存在的两个变量分别是什么?
(2)温度T取到一个定值时,时间t是否唯一确定?请说出该地区t=12时的温度。
通过引导提问,让学生从直观上感受函数一一对应的关系,理解“唯一确定”的含义,明晰函数概念。
函数是从数量角度来反映变化规律的模型,对于函数概念的“变化”和“对应”思想,教师要进行有针对性的设计,通过引导设问的方式使学生从图象的直观感受上理解函数的特性,让学生的思维经历质的飞跃。
二、结合生活实例,体验概念的生成
数学教学应该是活动式的教学,对于抽象的数学内容,教师更要精心设计数学情境,从生活实例中提炼丰富的素材,并将其转化为数学知识,让学生体验数学的探究过程,并建立起对函数知识的认识。
对于“变量与函数”的教学,教师应由实际问题来抽象函数概念,引导学生经历概念的形成过程,正确理解函数的意义,了解函数的本质。首先从生活的实例中让学生感知变量,深刻体会学习变量的必要性。例如,在教学中让学生体会自己的成长经历,随着年龄的增加,大家身体长高、体重增加、知识增多等,这些都可以看作是变量。紧接着就要引导学生明晰变量和常量的概念,如:①以60千米/时匀速行驶的汽车,它的里程随时间的变化而变化;②某地一天内各时刻的气温变化;③悬挂重物的弹簧,它的长度随质量的变化而变化。首先引导学生发现规律:存在数值变化的量和数值不变的量,然后指出实例中哪些是变量,哪些是常量,最终反复分析、比较、抽象、概括出变量与常量的概念。针对实例中的某一问题让学生分组讨论,分析问题中的两个变量之间是否存在联系,存在怎样的联系。教师要密切关注和了解各组的讨论情况,适时点拨。例如问题1,存在变量时间t,变量里程s,两个变量存在联系,即其中一个变量取一定值时,另一个变量是唯一确定的,如t=1时,s=60;t=2时,s=120。然后引导学生归纳概括,得出问题中变量与变量之间的共同属性:①存在两个变量;②变量之间存在联系;③一个变量的变化会引起另一个变量发生变化;④这种变化呈一一对应关系。最后,引导学生用规范的数学语言表述函数的概念。
可见,结合实例开展探究活动,并根据实例进行有针对性地分析和比较,不仅有利于学生掌握函数的本质,也能提升学生分析概括的能力。
三、合理引用反例,辨析函数的特征
函数概念的形成需要经历“观察—分析—比较—概括—表述”的过程,学生对于概念的认识将经历从模糊到清晰。教学中合理地运用反例可以帮助学生深刻理解函数的概念,但是反例的运用需要细致斟酌,过多、过早都会对学生的理解造成干扰。
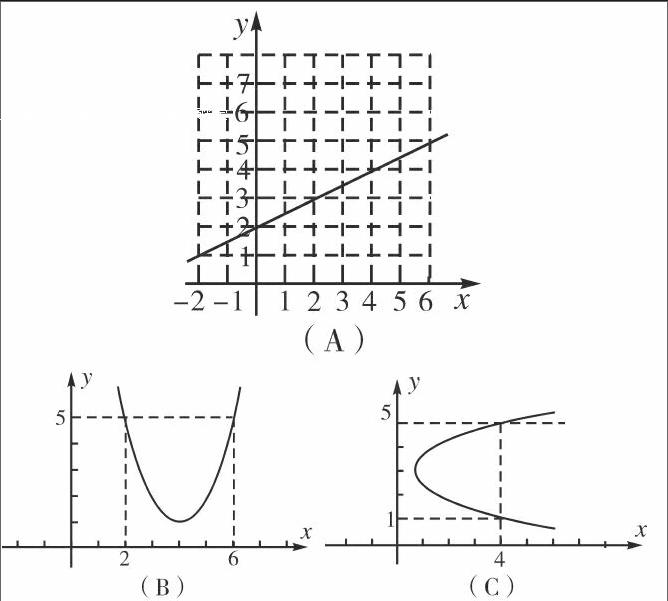
概念探究的前期需要大量的实例作为背景,由实例来抽象出变量关系,从中概括出函数“单值对应”的特殊关系。该过程需要充分引入反例,通过正反对比让学生有效避开概念理解的误区。例如由“气温问题”的函数图象向学生讲解“唯一确定”时不需要设置反例,反例的设置只会使学生失去学习重点,但对于函数概念的“唯一对应”则可以设置反例,通过辨析帮助学生理解该特征的实质:这样的对应可以是“一对一”,也可以是“多对一”,但不可以是“一对多”(实例如下图)。
在教学“一个变量确定另一个变量”时,可以对引用的实例进行反例辨析,例如对于“汽车匀速行驶问题”和“气温问题”作出如下变式提问:①该地区某一天的时间是气温的函数吗?②该汽车以每小时60千米的速度匀速行驶,时间t是里程s的函数吗?巧妙运用反例,可以帮助学生根据生活经验理解“两个变量的对应关系”,即“变量A能唯一确定变量B”,理解自变量与函数的关系,进而培养学生逆向思维能力。
单纯地观察同一属性的事物很难明晰事物的共同属性,而对事物的充分认识是从对比中发展而来的,没有对比就没有区分,反例的合理运用则可以帮助学生把握事物的共同特征。
“变量与函数”的教学是首次在常量的基础上引入了变量,是学生对数学认知的深入递进。教师要充分结合实例,遵循感性到理性、具体到抽象的认知规律,充分把握函数的“变化”与“对应”思想,合理利用正、反实例,通过对比分析帮助学生理解函数的本质特征。
(责编 林 剑)endprint
