立足基础 提升能力

梁小玲

摘 要：立体几何是高中数学教学的重要内容，而立体几何的教学重点是帮助学生逐步形成空间想象能力。以2013学年广州市高二年级学生学业水平数学测试中的试题为例，反思作为一个教师，在教学中该如何以学生为主体，促进学生特别是文科生立体几何知识的掌握和解题能力的提高。

关键词：空间想象能力；反思；文科生

一、问题的提出

立体几何是高中数学教学的重要内容，无论是教学大纲还是新课程标准中，立体几何的教学重点都是帮助学生逐步形成空间想象能力。空间想象能力是数学教学中需要培养的基本能力之一，它是空间能力所包含的一个因素，又以空间观念为基础。但随着新课程标准的全面推行，对高中学生的空间想象能力和推理论证能力的要求和以前的大纲版教材有所变化，把重点转移到了运算上。特别是随着空间向量知识在新课程标准教材中的引入，使得立体几何中论证和运算问题变得程序化了，因此，对于理科生，很多老师在教学中都要求他们运用向量法，因为空间坐标向量法只要建立适当的空间坐标系，很多问题都能迎刃而解。但作为文科生，空间向量坐标法在新课程标准中是不作要求的，作为教师，怎样才能使学生在只有一种解题工具——综合法的情况下，促进学生立体几何知识的掌握和解题能力的提高？本文以2013学年广州市高二年级学生学业水平数学测试中的试題为例，反思作为一个教师，在教学中该如何以学生为主体，将教师的“教”让道于学生的“悟”，从而提高学生的的空间想象能力和推理论证能力。

二、试题与讲评建议

题目（2013学年广州市高二年级学生学业水平数学测试第17题）

如图1，在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是A1D1，A1A的中点。

（1）求证：BC1∥平面CEF；

（2）在棱A1B1上是否存在点G，使得EG⊥CE？若存在，求A1G的长度；若不存在，说明理由。

教研室给出的讲评建议是：本考题改编于人教A版必修2P83A组第九题，主要考查线面平行和证明异面直线垂直。

三、教研室给的参考答案

证明：（1）如图2，连接AD1，∵AB■C1D1，∴ABC1D1是平行四边形，所以BC1∥AD1，又E，F分别是A1D1，A1A的中点，所以EF∥AD1，所以BC1∥EF，又BC1在平面CEF外，EF在平面CEF内，所以BC1∥平面CEF。

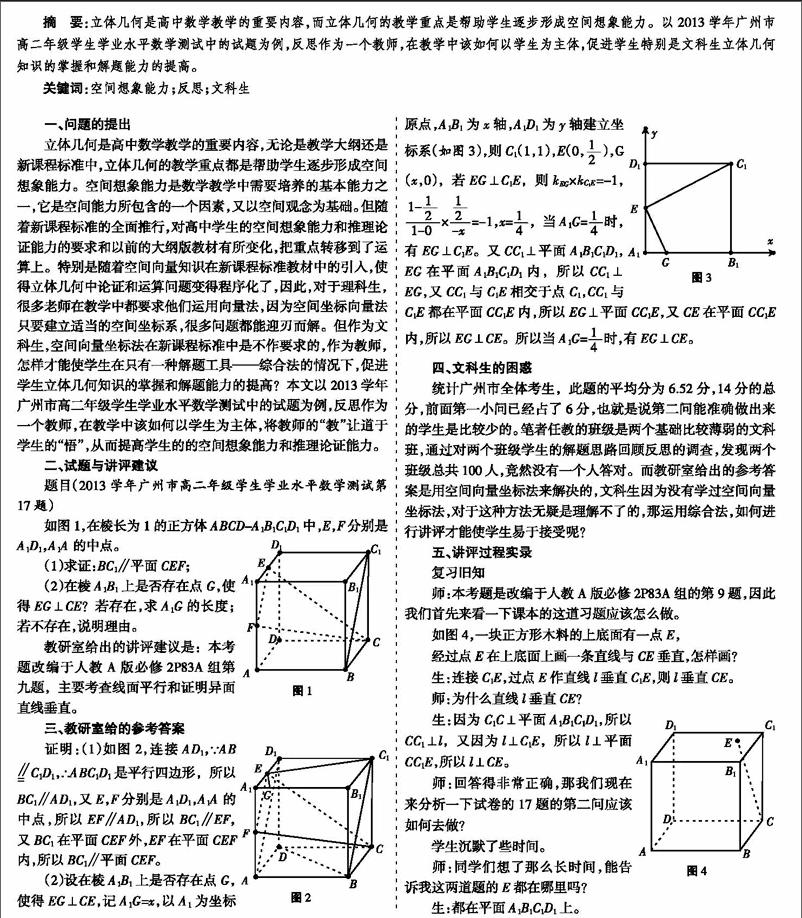
（2）设在棱A1B1上是否存在点G，使得EG⊥CE，记A1G=x，以A1为坐标原点，A1B1为x轴，A1D1为y轴建立坐标系（如图3），则C1（1，1），E（0，■），G（x，0），若EG⊥C1E，则kEG×■=-1，■×■=-1，x=■，当A1G=■时，有EG⊥C1E。又CC1⊥平面A1B1C1D1，EG在平面A1B1C1D1内，所以CC1⊥EG，又CC1与C1E相交于点C1，CC1与C1E都在平面CC1E内，所以EG⊥平面CC1E，又CE在平面CC1E内，所以EG⊥CE。所以当A1G=■时，有EG⊥CE。

四、文科生的困惑

统计广州市全体考生，此题的平均分为6.52分，14分的总分，前面第一小问已经占了6分，也就是说第二问能准确做出来的学生是比较少的。笔者任教的班级是两个基础比较薄弱的文科班，通过对两个班级学生的解题思路回顾反思的调查，发现两个班级总共100人，竟然没有一个人答对。而教研室给出的参考答案是用空间向量坐标法来解决的，文科生因为没有学过空间向量坐标法，对于这种方法无疑是理解不了的，那运用综合法，如何进行讲评才能使学生易于接受呢？

五、讲评过程实录

复习旧知

师：本考题是改编于人教A版必修2P83A组的第9题，因此我们首先来看一下课本的这道习题应该怎么做。

如图4，一块正方形木料的上底面有一点E，

经过点E在上底面上画一条直线与CE垂直，怎样画？

生：连接C1E，过点E作直线l垂直C1E，则l垂直CE。

师：为什么直线l垂直CE？

生：因为C1C⊥平面A1B1C1D1，所以CC1⊥l，又因为l⊥C1E，所以l⊥平面CC1E，所以l⊥CE。

师：回答得非常正确，那我们现在来分析一下试卷的17题的第二问应该如何去做？

学生沉默了些时间。

师：同学们想了那么长时间，能告诉我这两道题的E都在哪里吗？

生：都在平面A1B1C1D1上。

师：那类似前面的做法，我们要怎么做？

生：连接C1E，过点E作直线EG垂直C1E交线段A1B1于点G然后证明EG⊥平面CC1E，则EG⊥CE。

师：很好，这样我们就找到了点G，接下来我们就要求A1G的长度，如何求A1G的长度？

生：证明三角形A1EG与三角形D1C1E相似，然后利用相似三角形定理来求解。

师：非常好！看来，大家已经在不知不觉中把这个问题解决了，那现在请同学们把解题步骤写出来。

解：（2）

连接C1E，过点E作直线EG⊥C1E叫线段A1B1于点G

∵CC1⊥平面A1B1C1D1，

∴CC1⊥EG，又∵EG⊥C1E，

∴EG⊥平面CC1E，∵EG⊥CE

∵∠C1EG=90°，∴∠A1EG+C1ED1=90°

又∵∠D1C1E+C1ED1=90°，∴∠A1EG=∠D1C1E，

∴Rt△GA1E∽Rt△E1DC1，∴■=■，

又∵A1E=ED1=■，D1C1=1，∴A1G=■=■，

六、教学反思

从上面的解法可看出，综合法比空间向量坐标法更简洁，而空间向量坐标法不仅要建立适当的空间直角坐标系，还涉及了三维空间中两直线垂直的相关结论，在这里不管是建立空间直角坐标系还是三维空间中两直线垂直的相关结论，对文科生特别是一些基础薄弱的文科生来说都是一个难点，但是综合法在这里渗透了初中的相似三角形的知识，这个知识点大部分学生都掌握得比较好，因此综合法比空间向量坐标法更易于学生接受。

“最近发展区理论”认为，学生的发展有两种水平：一种是学生的现有水平，另一种是学生可能的发展水平。两者之间的差距就是最近发展区。因此，教师在教学中应着眼于学生的最近发展区，在讲授有难度的内容时，要发挥其潜能，超越其最近发展区从而达到更高的水平，并在此基础上进行下一个发展区的发展。比如，在此题讲评时，笔者不是告知学生此题考查的知识点，“教”给学生解题的方法，而是从学生熟悉的问题出发，逐步过渡到所要解决的问题，进而完善学生的知识结构和方法体系，达到提升学生思维能力的目的。

如在试卷讲评中，教师对于学生做错的题目要充分考虑学生的实际情况，解题方法不要过于麻烦，否则不仅不会引起学生的兴趣，而且会使学生对数学产生畏惧感。新课标要求从学生的实际情况出发，让学生养成自主学习的习惯和观念，鼓励学生在学习生活中多实践。学生是课堂的主人，任何教学活动的设计都应遵循学生的认知规律，尊重学生的思维，尊重学生的情感，因此试卷讲评中，教师要明确自己此时的任务是“促进学生逐步形成和发展数学应用意识，提高实践能力”。

参考文献：

[1]赵炜.“教”让道于“悟”[J].中学数学月刊，2013（9）.

[2]蔡萍，高月华，张晓琦.培养空间想象能力的教法探索[J].重庆科技学院学报，2005（2）.

[3]董成勇.高中生学习空间向量的困难和相应的教学策略[D].华东师范大学，2007.

编辑 郭小琴endprint