基于Prony算法的基波频率测量方法＊

姜毅龙，李许军，王春霞

（1.甘肃机电职业技术学院，甘肃天水741001；2.兰州理工大学计算机与通信学院，甘肃兰州730050）

基于Prony算法的基波频率测量方法＊

姜毅龙1，李许军1，王春霞2

（1.甘肃机电职业技术学院，甘肃天水741001；2.兰州理工大学计算机与通信学院，甘肃兰州730050）

针对电网频率跟踪测量的问题，提出了一种基于Prony算法的基波频率测量方法。首先通过CIC组合滤波器从原始信号中提取出基波信号，再利用Prony算法进行频率跟踪测量。该方法可以有效地抑制原始信号中的直流、谐波和噪声，降低测量系统的基波频率测量偏差。实验仿真结果表明，该算法响应速度快，测量精度高，测量结果满足电网监测和电能计量的精度要求。

Prony算法；基波提取；CIC滤波器；频率测量

1 引言

电网频率是衡量电网电能质量的重要依据，也是影响电能计量准确度的关键。准确测量电网的基波频率是智能化电网监控、电能计量的重要保障。近年来，电网频率的测量算法主要有FFT变换法［1］、小波变换法［2］、Kalman 滤波法［3］、最小二乘法［4、5］、正交滤波器法［6］以及自适应滤波［7、8］法等。这些算法在应用过程中通过不断改进或相互结合，解决了电网频率跟踪测量的问题，同时各自存在着一定的局限性。文献［9、10］利用锁相环电路来抑制输入信号中的直流、谐波和噪声，提高基波的测量准确度；文献［11］通过奇异值分解的逆过程对原始信号进行了重构，提取了基波信号，利用总体最小二乘－旋转矢量不变技术估算了基波频率；文献［12］利用小波变换与三点法相结合的方法测量了电网中的基波频率，但该方法实时性较低；文献［13］通过改进的Duffing方程对电网基波频率实现了检测，具有良好的噪声免疫特性和检测精度；文献［14］结合硬件测频法和软件测频法的优点，提出了一种基于线性插值的电网频率测量方法，具有良好的测量效果；文献［15］通过自适应算法实现了基波提取，引入鲁棒扩展卡尔曼滤波算法实现了基波频率的精确跟踪，该算法具有良好的抑制电网谐波和噪声的效果。

针对电网基波频率的测量和跟踪问题，本文设计了一种基于Prony算法的基波频率跟踪测量方法。该方法通过多阶CIC滤波器从输入信号中精确地提取出基波信号，并在此基础上，引入Prony算法进行基波频率的测量。该方法可有效地抑制输入信号中的噪声干扰，并具有较好的实时性，能够准确测量并跟踪电网中基波频率的变化情况。

2 基波CIC滤波器的设计

CIC滤波器是典型的多速率数字滤波器［16］。基波CIC滤波器的作用是滤除输入信号中的直流、谐波和噪声成分。基波CIC滤波器第二阶级联的传递函数如式（1）所示，其作用是滤除输入信号中的直流分量和频率为ωS/2的部分，其在频率为ω1的基波分量上的增益为1。

图1 基波CIC滤波器的频率响应

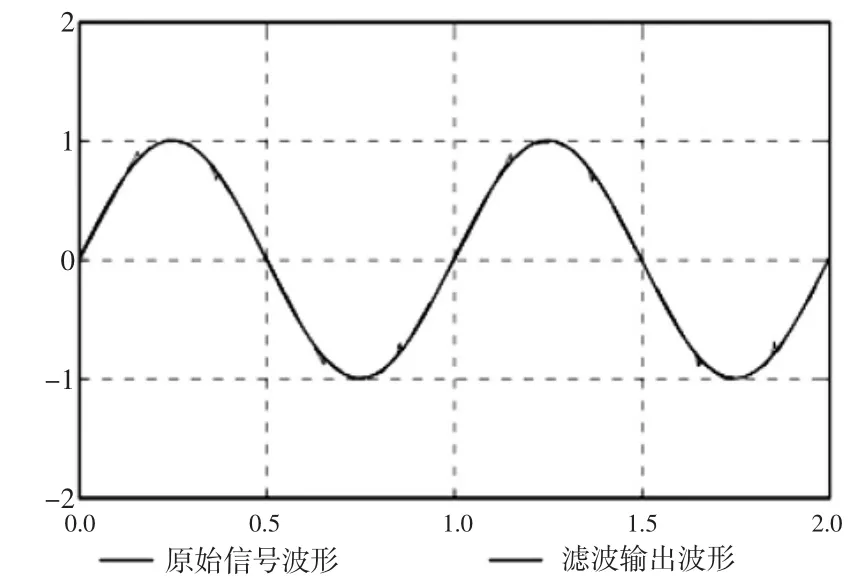
图2 含有谐波的基波CIC滤波输入输出对比波形

第i个级联滤波器传递函数表达式如式（2）所示，其作用是消除 ωi＝iω1谐波分量，且保证在 ωi的基波分量上增益为1。

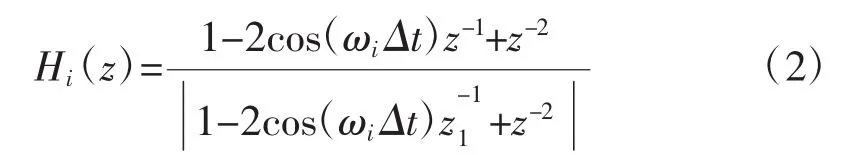
CIC滤波器的频率响应图如图1所示，其采样频率fs为1024Hz。利用这种多阶基波CIC滤波器可以有效地抑制原始信号中直流、谐波及噪声，其波形图如图2所示。

3 基于Prony的频率跟踪算法

3.1 Prony 算法描述

Prony算法是一种使用复指数函数的线性组合来近似描述一系列等间距采样数据的数学模型，通过一组p个复指数函数进行相关的运算和求解，其中复指数函数的幅值、相位、频率与衰减因子可以是任意的。利用Prony方法进行离散数据拟合的函数可表示为：

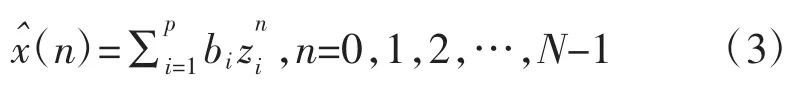
当用式（3）中p个指数项去逼近N（N≥2p）个数据时，可采用最小二乘法求解 Ai，ai，fi和 θi，使得的平方误差达到最小。这种非线性问题采用最小二乘法求解，其难度较大。而Prony算法将该非线性方程组转化成为一个高次代数方程和两个线性方程组求解获得次最佳解。因此，为了求解该线性差分方程，定义特征多项式，由式（3）可得：

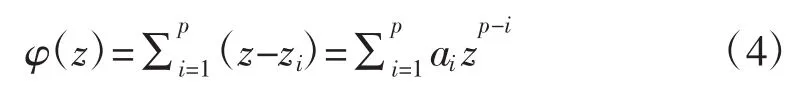
定义：

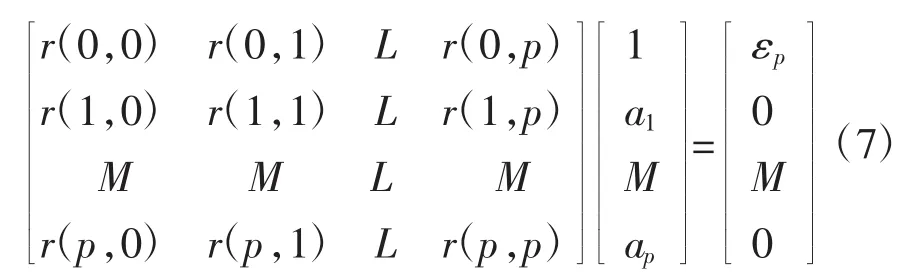
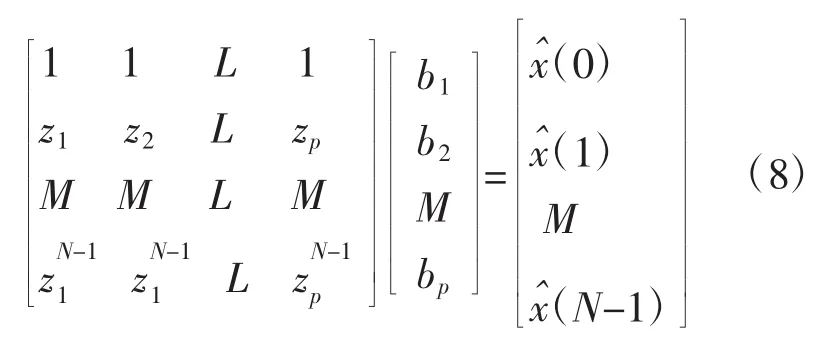
模型中 Ai、ai、fi、θi等参数可从 Prony 极点 zi和系数bi中求得。

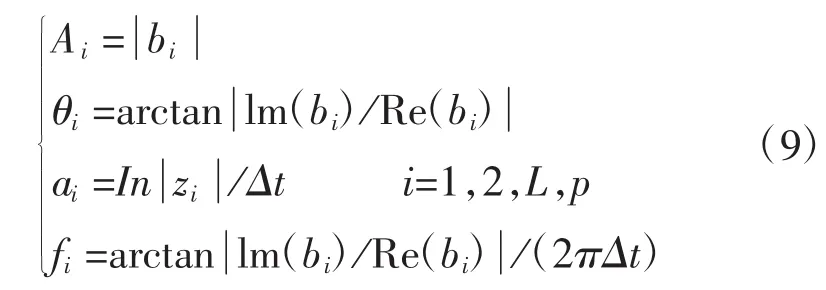
3.2 基于Prony的频率测量算法

假设经过CIC基波滤波器处理后的信号为纯余弦信号，则：

其复指数函数为：

由于Prony的关键是使误差最小，并将非线性问题转换为线性问题来处理。设误差E为：

参数ak的初始值未知，其与信号的频率有关。为了求解等式（11），建立统一的线性化形式，对于p＝2作如下定义：

z1和为上式的根，将式（13）代入式（15）可得：

通过式（13）和式（14）可得下式：

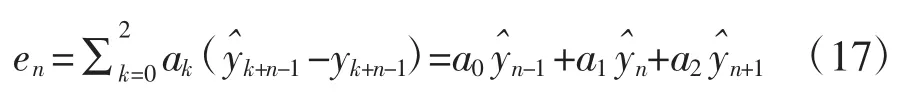
F（z）的解 z1是单位指数，即 z1是 F（z）的根，则也是 F（z）的根。因此系数 ak和 a1是相互对称的，a0＝a2。令 a1＝1，则有：

要使关于a0的E值最小，则对E求关于a0的偏导，如式（19）所示：

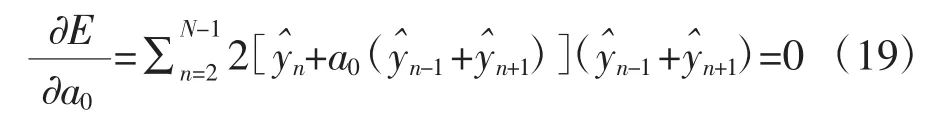
求解上式可得：

由此多项式F（z）可以表示为：

求解可得：

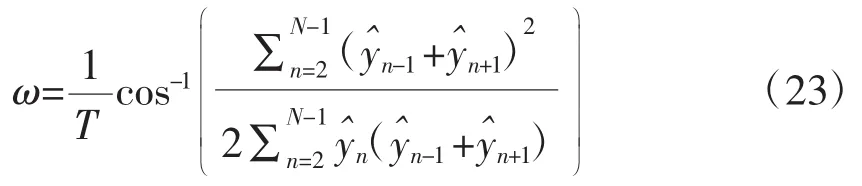
4 实验验证

为了验证以上所提方法的准确性，分别建立缓变频率的正弦信号 f＝50＋0.2sin（8πt）Hz和突变频率信号作为被测信号源，利用以上算法进行基波频率测量和跟踪的仿真实验。设采样频率fs为1024Hz，M＝1，则其仿真结果如图3和图4所示。

图3 正弦缓变频率模型测量结果

图4 线性频率模型测量结果

从图3和图4可以看出，基于Prony算法的基波频率测量和跟踪均能较好地对每个时刻的采样数据进行跟踪并能实时更新，其测量结果较为准确，测量偏差小于0.5%，可以满足电网频率的实时监测要求。

5 结束语

本文提出的基于Prony算法的基波频率测量方法，通过CIC滤波器从输入信号中精确地提取出基波信号，并在此基础上，引入Prony算法完成了基波频率的精确测量和跟踪。仿真数据表明该方法能够有效地抑制电网谐波和噪声对测量结果的影响，其算法实时性较高，可以满足电网状态监测和电能计量的实际应用要求。

［1］李一泉，何奔腾.一种基于傅氏算法的高精度测频方法［J］.中国电机工程学报，2005，26（2）：78－81.

［2］黄荣雄，吴杰康，韦善革.基于小波变换的电力系统谐波频率测量算法［J］.电力学报，2010，25（3）：193－196.

［3］Huang C H，Lee C H，Shih K J，et al.Frequency estimation of distorted power system signals using a robust algorithm［J］.IEEE Transactions on Power Delivery，2008，23（1）：41－51.

［4］麦瑞坤，何正友，何 文，等.电力系统频率的自适应跟踪算法［J］.中国电机工程学报，2010，30（16）：73－78.

［5］Chudamani R，Vasudevan K，Ramalingam C S.Real－time estimation of power system frequency using nonlinear least squares［J］.IEEE Transactions on Power Delivery，2009，24（3）：1021－1028.

［6］El－Shafey M H，Mansour M M.Application of a new frequency estimation technique to power systems［J］.IEEE Transactions on Power Delivery，2006，21（3）：1045－1053.

［7］M Mojiri，M K Ghartemani，A Bakhshai.Estimation of power system frequency using an adaptive notch filter［J］.IEEE Transactions on Instrumentation and Measurements，2007，56（6）：2470－2477.

［8］C H Huang，C H Lee，K J Shih.Frequency estimation of distorted power system signals using a robust algorithm［J］.IEEE Transaction on Power Delivery，2008，23（1）：41－51.

［9］门长有，王荣华，谭年熊.基于全数字锁相环的基波频率测量算法［J］.电路与系统学报，2011，16（6）：30－34.

［10］王硕禾，许继勇，等.联合三相锁相环和优化三点法的供电频率高精度测量算法［J］.电力自动化设备，2012，32（1）：88－92.

［11］黄 奂，卢 泉，黄 阳，陈邕安.基于奇异值分解和总体最小二乘－旋转矢量不变技术的电力系统基波频率测量方法［J］.电测与仪表，2014，51（16）：78－83.

［12］应展烽，吴军基，易文俊.基于小波变换和三点法的基波频率测量［J］.电机与控制学报，2010，14（2）：66－70.

［13］刘 强，李果繁，曾喆昭.基于新型Duffing振子的电网基波频率检测方法［J］.电力科学与技术学报，2015，30（3）：78－82.

［14］宋红卫.基于线性插值的电网频率测量方法［J］.工矿自动化，2012，（6）：99－102.

［15］张 斌，张东来.电力系统自适应基波提取与频率跟踪算法［J］.中国电机工程学报，2012，31（25）：81－89.

［16］刘国稳，朱卫华.高性能CIC滤波器的优化设计［J］.计算机仿真，2016，33（2）：234－238.

Research on fundamental frequency measurement based on Prony algorithm

JIANG Yi－long1，LI Xu－jun1，WANG Chun－xia2
（1.Gansu Institute of Mechanical＆ Electrical Engineering，Tianshui 741001，China；2.College of Computer and Communications，Lanzhou University of Technology，Lanzhou 730050，China）

Aiming at the problem of frequency tracking measurement of power grid，a method of fundamental frequency measurement based on Prony algorithm is proposed.Firstly，the fundamental signal is extracted from the original signal by CIC composite filter，and then the Prony algorithm is used for frequency tracking measurement.The method can effectively suppress the DC，harmonic and noise in the original signals，also can reduce the measurement error for the fundamental frequency of the measurement system.The simulation results show that the algorithm has high response speed and high measuring precision，and it can satisfy the accuracy requirements of the power network monitoring and the energy metering.

Prony algorithm；fundamental component extraction；CIC filter；frequency measurement

TP206＋.1

A

1005—7277（2017）03—0001—04

2017年甘肃省高等学校科研项目（2017B－14）；

2016年天水市科技支撑计划项目（天财科［2016］496号）

姜毅龙（1966－），男，甘肃会宁人，本科，副教授，主要研究方向为单片机嵌入式技术。

李许军（1981－），男，甘肃天水人，硕士研究生，讲师，主要研究方向为电子测量技术。

2017－01－11