高强度管线钢拉伸试验伸长率变化规律研究和分析*

，，， ，，记科

(中国石油集团石油管工程技术研究院 陕西 西安 710077)

高强度管线钢拉伸试验伸长率变化规律研究和分析*

许晓锋，秦长毅，梁明华，李娜，蔺卫平，李记科

(中国石油集团石油管工程技术研究院 陕西 西安 710077)

针对高强度管线钢拉伸试验伸长率换算遇到的问题，选用多种高强度管线钢材料对其拉伸试验伸长率变化规律进行了研究，对大量拉伸试验数据进行了统计分析。试验结果表明，基于碳素钢和低合金钢旧材料建立的Oliver公式仍适用于高强度管线钢，但材料系数有所变化。建立了X65～X90钢级管线钢拉伸试验伸长率变化公式及50 mm固定标距高强度管线钢伸长率变化公式。根据新的材料系数和公式对伸长率要求值和试验值进行了比对分析，给出了更加合理的技术要求。

高强度；管线钢；伸长率；变化规律；Oliver公式

0 引 言

拉伸试验伸长率是反映材料塑性的重要指标，对工程安全有一定的影响[1]。关于高强度管线钢小尺寸试样拉伸试验伸长率的技术要求，现行管线钢管产品标准和拉伸试验方法标准存在一些问题[2]，影响了标准的执行和产品质量的评判。

文献[2]选用多种X80管线钢材料对其拉伸试验伸长率变化规律进行了研究。试验结果表明，基于碳素钢和低合金钢旧材料建立的Oliver公式仍适用于X80高强度管线钢，但材料系数不同。由于试验数据有限，获取的材料系数(0.69)可信度不够高。为进一步论证Oliver公式对于高强度管线钢的适用性并计算更准确的材料系数，探讨更合理的伸长率技术要求，本文进行了深入研究和分析。

1 研究内容

随机选取10个高强度管线管拉伸试验样品，测量并计算不同标距对应的伸长率值，进一步论证Oliver公式对于高强度管线钢的适用性。

基于力学试验积累的大量试验数据，建立高强度管线钢拉伸试验伸长率数据库，统计分析X65、X70、X80和X90高强度管线钢伸长率公式的材料系数。

结合标准要求，计算并确立高强度管线钢50 mm固定标距伸长率变化规律公式，对比分析要求值与试验值的差异，给出更合理的标准技术要求建议。

2 结果及分析

2.1 Oliver公式适用性

随机选取试样的测量结果和分析结果见表1，试样不同标距对应伸长率值的拟合情况如图1所示。

表1 试样不同标距对应断后标距及其关系

图1 试样不同标距对应伸长率值的拟合曲线

从分析结果来看，单个试样伸长率值拟合曲线的线性相关系数都接近1.0，说明其伸长率的变化规律完全符合Oliver公式。随机选取的试样屈服强度从656 MPa到740 MPa，抗拉强度从748 MPa到884 MPa，其强度级别覆盖了X80、X90和X100。可见，Oliver公式在高强度管线钢方面具有普遍适用性。

2.2 不同钢级材料Oliver公式

为获得不同强度等级管线钢更为准确的材料系数，需要对大量试验数据进行统计分析。基于力学试验积累的大量试验数据，建立了高强度管线钢拉伸试验伸长率数据库，本文对数据库中2 965条试验数据进行了分析，统计分析结果如图2所示，统计分析数据见表2。

从图2和表3的统计分析结果来看，拟合曲线的线性相关系数较高，各钢级材料整体分析的相关系数都在0.94左右，结果比较理想。由此建立各钢级材料的伸长率变化公式见式(1)～式(4)。

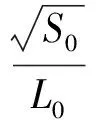
(1)

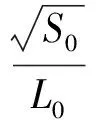
(2)

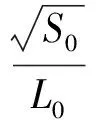
(3)

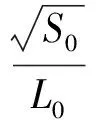
(4)

各钢级管线钢的材料系数不尽相同，由此可见，伸长率值与材料强度级别、试样横截面积和标距长度有关。API Spec 5L标准拉伸试验要求给出的固定标距伸长率计算公式也说明这一点。API标准中为便于试样结果的比较，规定测量试样50 mm标距长度的伸长率值，并给出了计算公式，见公式(5)。

(5)

将新建立的公式与公式(5)进行比较，我们发现公式中与试样横截面积相关的指数存在明显差异，这种差异的原因在下文进行了分析。

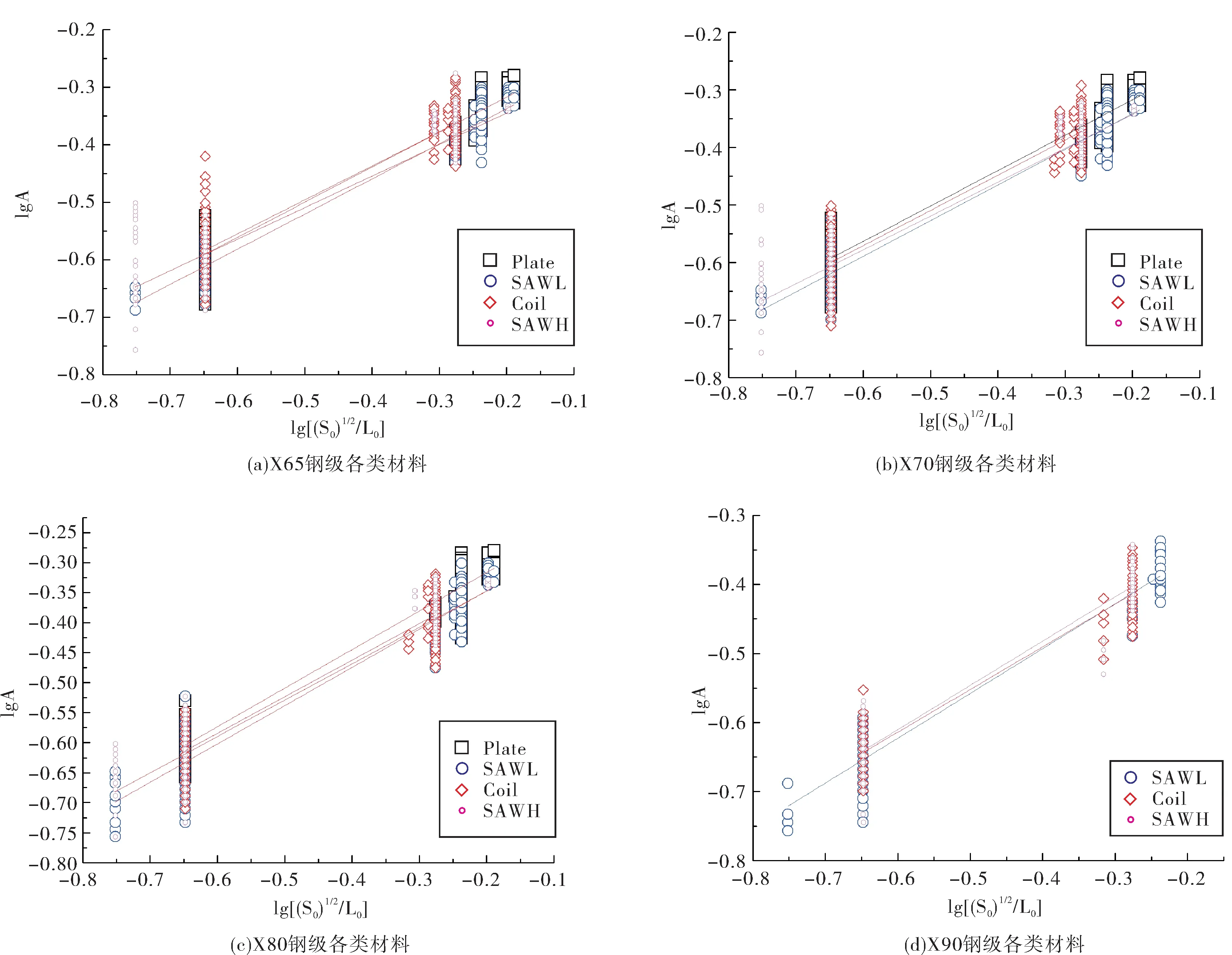
图2 高强度管线钢拉伸试验伸长率变化规律统计分析

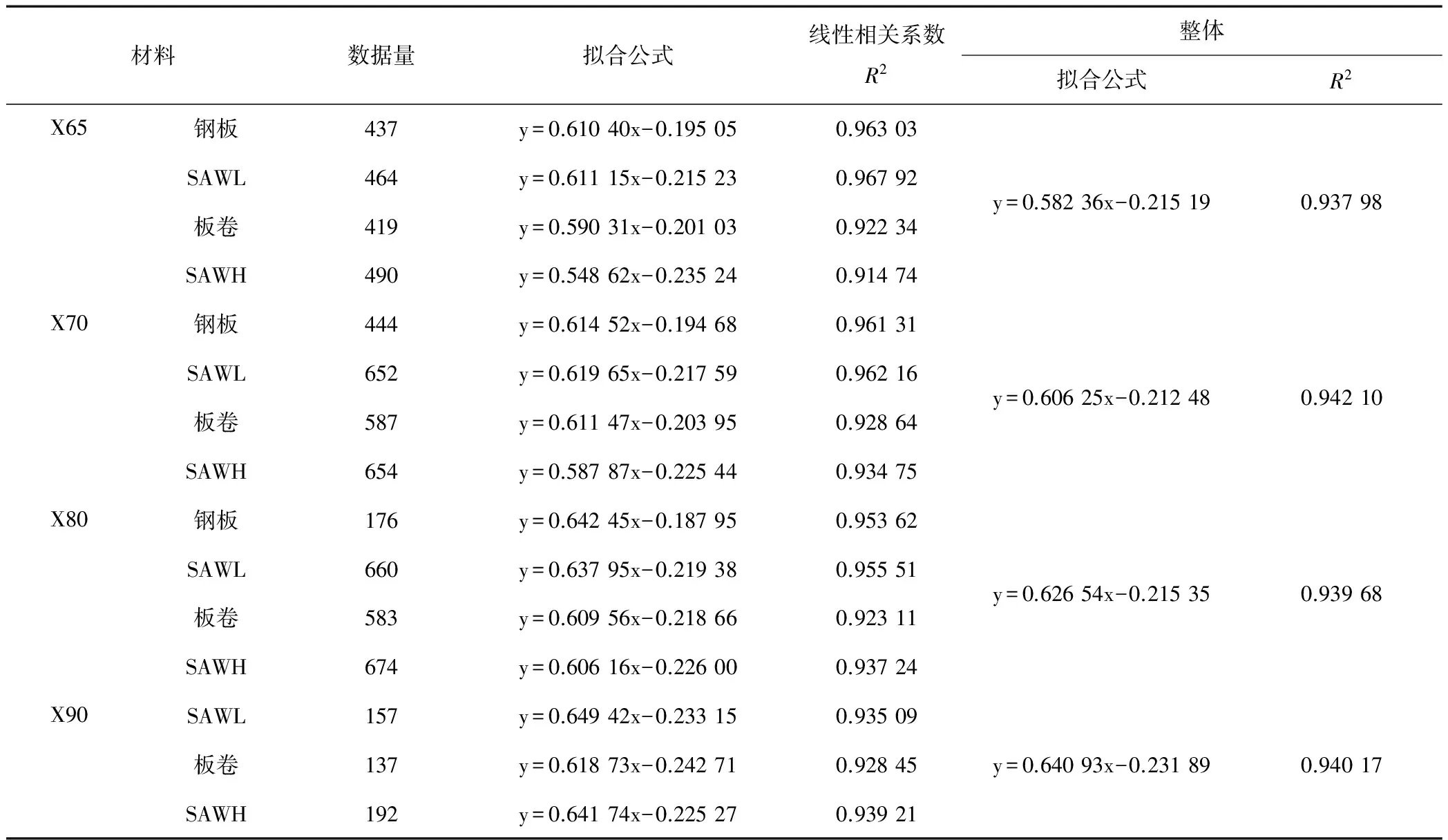
表2 统计分析数据量及拟合曲线公式

2.3 50 mm固定标距伸长率变化规律

基于伸长率试验数据库，我们对高强度管线钢50 mm固定标距伸长率的变化规律进行了分析。

根据公式(5)的表达关系，我们经过线性化处理得到：

logA=alog(S0)+blog(Rm)+logC

(6)

式中：A为断后伸长率；S0为试样原始横截面积；Rm为材料抗拉强度；a、b为与横截面积和强度有关的指数，C为与公式相关的常数。

拟合得到的数据见表3。

根据整体数据的分析，我们得到高强度管线钢50 mm固定标距伸长率值百分数的计算公式为公式(7)所示。

(7)

实测值、现标准要求值和公式(7)拟合值的对比关系如图3所示。

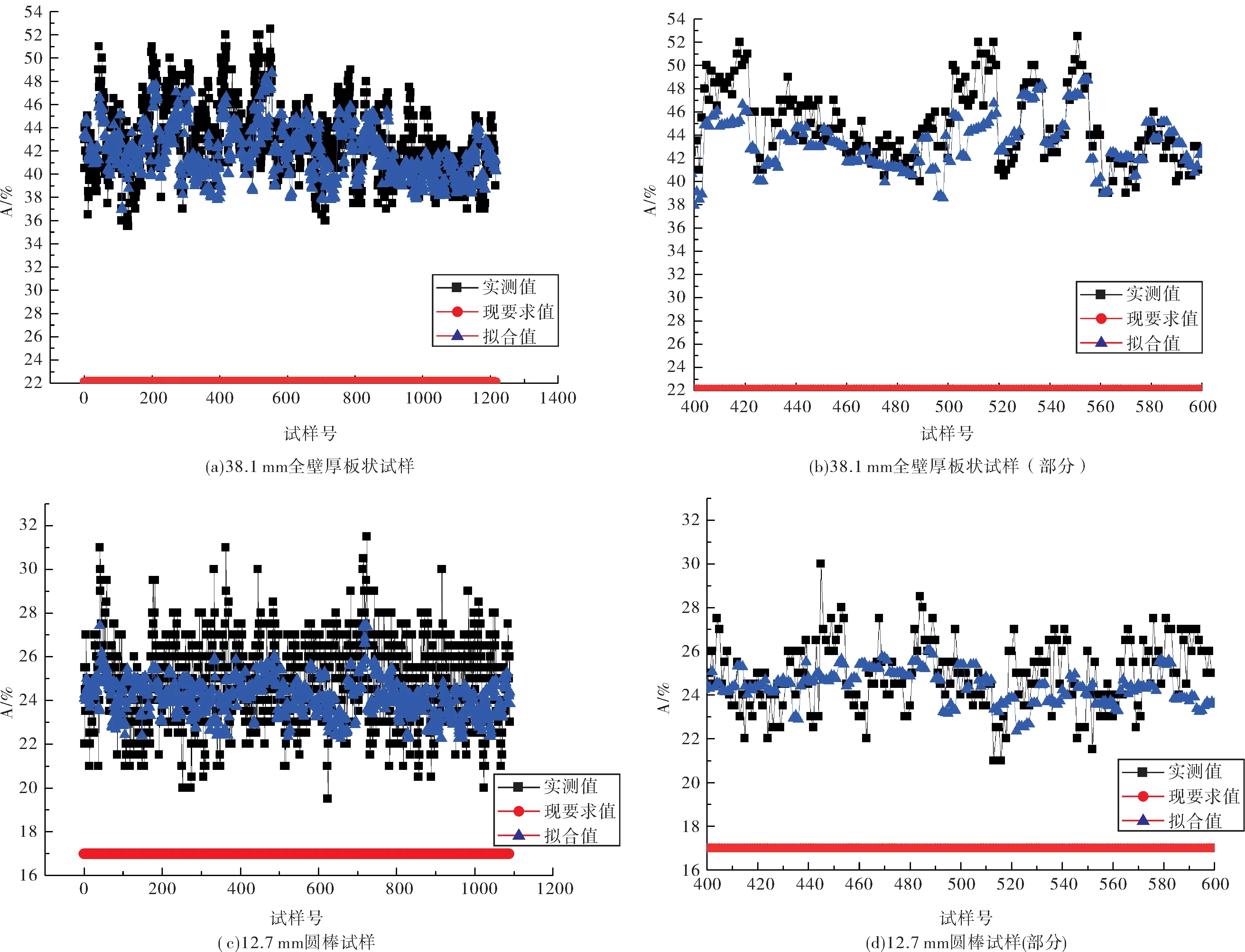
图3 实测值、现标准要求值和新公式拟合值的比对

通过对比，我们能明确得出如下两个结论：1)公式(7)拟合值很好地模拟了材料的真实性能；2)现标准要求值与实测值得差距较大，特别是板状试样，已不能很好地发挥控制材料性能的作用。那么，采用什么值作为该性能的技术要求呢？为反映该技术要求对材料性能的真实约束，建议应以公式(7)为基础来确定合适的技术要求。当公式中强度值取最大抗拉强度时，得到一个相对较小的值，大部分试样的试验值会高于该值；若取小于1的倍数值，则更多的试样可以满足这个要求。本文针对X70钢级产品，强度值分别取最大抗拉强度、0.95倍最大抗拉强度、0.9倍最大抗拉强度和0.85倍最大抗拉强度四种情况进行了分析，其中两种情况如图4所示。

图4 取不同倍数最大抗拉强度时数据比较

分析的2 306个试验数据，38.1 mm全壁厚板状试样有1 216个，直径12.7 mm圆棒试样有1 090个。当强度取最大抗拉强度时，板状试样中有43个试验值低于此时的计算值，占比3.5%；棒状试样中有95个试验值低于此时的计算值，占比8.7%。取0.95倍最大抗拉强度时，板状试样中有4个试验值低于此时的计算值，占比0.3%；棒状试样中有32个试验值低于此时的计算值，占比2.9%。取0.9倍最大抗拉强度时，仅棒状试样中有1个试验值低于此时的计算值。取0.85倍最大抗拉强度时，所有试验值不低于此时的计算值。

数据库中数据来源于目前认为是合格的材料，因此认为将强度值确定为0.85倍最大抗拉强度并以此计算值作为标准技术要求是可以接受和合理的。综上所述，高强度管线钢拉伸试验伸长率技术要求建议采用公式公式(7)进行计算，计算时公式中强度值取对应钢级材料规定最大抗拉强度的0.85倍。

3 结 论

1)随机选取多个试样，开展了高强度管线钢拉伸试验伸长率变化规律的补充试验，试验结果表明Oliver公式在高强度管线钢方面具有普遍适用性。

2)基于力学试验数据库，对高强度管线钢拉伸试验伸长率变化规律进行了统计分析，获得了更准确反映X65、X70、X80和X90高强度管线钢拉伸试验伸长率变化规律的Oliver公式。

3)确立了高强度管线钢50 mm固定标距伸长率变化规律公式，并对试验值和要求值进行了对比分析。发现标准现要求值太过宽松，不能真实反映材料性能并进行有效约束，而新拟合公式能很好地反映材料真实性能，因此提出建议以公式(7)为基础来确定合适的技术要求。

[1] 束德林.金属力学性能[M].北京机械工业出版社,1999:1-48.

[2] 许晓锋,秦长毅,李 娜,等.X80高强度管线钢拉伸试验伸长率变化规律研究[J].焊管,2016,39(9):6-12.

StudyandAnalysisonTensileTestElongationVariationLawforHighStrengthPipelineSteel

XUXiaofeng,QINChangyi,LIANGMinghua,LINa,LINWeiping,LIJike

(CNPCTubularGoodsResearchInstitute,Xi’an,Shaanxi710077,China)

In view of the tensile test elongation conversion proble ms for high strength pipeline steel, several kinds of high pipeline steel materials were selected to conduct the study on the tensile test elongation variation law, and a statistical analysis was carried out based on a great many test data. The tests results showed that Oliver formula, which was established based on old carbon steel and low alloy steel material, is still applicable to high strength pipeline steel but with different material coefficients. The tensile test elongation variation formulae for X65 to X90 high grade pipeline steels and the formula for high strength pipeline steel with a fixed 50 mm gauge length were established. The comparison between the test data and required data was analyzed according to the new material coefficient and formula, then a more reasonable revision suggestion for the standard was put forward.

high grade; pipeline steel; elongation; variation law; Oliver formula

国家质检公益性行业科研专项经费资助(编号：201510205-03)。

许晓锋，男，1982年生，高级工程师，2007年毕业于中国石油大学(华东)材料加工工程专业，现主要从事石油管材标准化工作。E-mail: xuxiaofeng009@cnpc.com.cn

TE973.1

A

2096-0077(2017)05-0027-05

10.19459/j.cnki.61-1500/te.2017.05.007

2017-03-22编辑葛明君)