例谈类比法在数学解题中的应用
2017-12-06首都师范大学数学科学学院100048覃淋
首都师范大学数学科学学院100048 覃淋
例谈类比法在数学解题中的应用
首都师范大学数学科学学院100048 覃淋
将“杨辉三角”与类比法相结合,讨论了三个著名的问题,并给出了比较简洁的计算方法.最后从现代认知心理学的角度讨论了类比法在数学学习中的重要性.
杨辉三角;类比;应用
杨辉三角,又称贾宪三角,国外通常称为帕斯卡三角形,是二项式系数在三角形中的一种几何排列.南宋数学家杨辉在其著作《详解九章算法》(1261)中,记载了贾宪的著作—《黄帝九章算术细草》里面的大部分内容.其中有一张称为“开方作法本源”的图,根据杨辉的记述,贾宪的高次开方法即以此为基础.下图是我国数学家朱世杰《四元玉鉴》中的“古法七乘方图”.[1]

图1

图2
关于杨辉三角的性质,已有很多的讨论[2-5],这里我们从类比的角度,来讨论杨辉三角的应用.类比法是数学发现发明的重要方法之一,比如将直角三角形与四面体进行类比,可以得到三维空间里的“勾股定理”;通过二维与高维空间的类比,将基本不等式和柯西不等式推广到了n维.历史上最著名的类比,当属欧拉求的和的类比,对于此,波利亚在其著作《数学的发现》中有详细的论述.
类比是某种类型的相似,我们可以说它是一种更确定的和更概念性的相似[6].简单地说,类比就是两类事物具有类似的关系,是一种从特殊到特殊的推理方法,建立在两类事物或对象具有相似性的基础上的.实际上,在数学中,处处都有类比的身影,数学中的同构实质上也是一种类比,两个同构的事物,具有一一对应的关系,那它们就可能有着保持某些关系不变的规律[7].
这里通过如下三个问题:1.剖分数问题,即讨论点分直线、直线分面、面分空间的问题;2.高维空间单位立方体的顶点数、棱数、“面”数问题;3.自然数幂和问题,来说明类比法在数学解题中的应用.
1 剖分数问题
这里我们讨论点分直线、直线分面、平面分空间这三个小问题.
(1)直线上n个点至多将一条直线分成多少部分?
(2)平面上n条直线至多将一个平面分成多少部分?
(3)空间中n个平面至多将空间分成多少部分?
为叙述方便,将以上三个问题分别称为“点分线”、“线分面”、“面分体”,然后再把最后分得的数目分别记为Ln,Sn,Vn.
分析 (1)这是一个比较简单的问题,只要任意两点不重合,那么n个点将一条直线分为n+1部分.作如下处理:

(2)要使得直线将平面分块最多,必然是任意两直线相交,且没有三直线共点.当n=0时,S0=1;n=1时,S1=2;n=2时,S2=4;n=3时,S3=7;n=4时,S4=11;...
实际上,每增加一条直线ln时,它就被原来的n-1条直线分成了n段;而这n段中的每一段又把原来的一个平面区域分割成两部分,也就是说,增加了n个,那么有:Sn=Sn-1+n,此时,

(3)要使“面分体”份数最多,即要求没有2个面平行,没有三个面共线,也没有4个平面共点.那么,当n=0时,V0=1;n=1时,V1=2;n=2时,V2=4;n=3时,V3=8;n=4时,V4=15;...
我们知道,原来的n-1个平面把空间分为Vn-1块,再添加一个平面,它与原来的n-1个平面有n-1条交线;那么新添的这个平面被分成Sn-1部分,这Sn-1中的每一部分又把一空间块分成2块,因此,Vn=Vn-1+Sn-1.此时:

将上面的结果整理,得到

_________________________________分成几部分分割元素的个数__________________ _________ _ _______点分线 线分面__ ____面分体____ _________________ ___ ___01___ _____1_____ ______1______ _________________ ___ ___12___ _____2_____ ______2______ _________________ ___ ___23___ _____4_____ ______4______ __________________ ___ 3 4___ _____7_____ ______8______ _________________ ___ ___45____ ____11____ ______15_____ _________________ ___ ___56____ ____16____ ______26_____ _________________ __……___ ____…____ ______…_____ __________________ _ nn+1__ _Sn-1+n_ _Vn-1+Sn-1__

图3
根据上面的分析,类比杨辉三角,得到了一个类似杨辉三角的图,我们称之为“杨辉式”三角(图3).对比左边的表格,斜着看右边的图,容易知道:第一“行”就是n=0时的情况,第二行是n=1时的结果,以此类推.
杨辉三角内的每一个数等于它左肩数与右肩上的数字之和.这里可以发现与之类似的规律:从第二行起,每一个数等于其正上方与右肩上数字之和.如15=7+8,11=4+7,若规定则有以下结论注意这里并没有要求n≥r.
2 高维空间立方体的顶点数、棱数、面数问题
一般来说,维数超过3的高维空间中“立方体”的结构及其特征是比较难以想象的,因为在实际生活中无法找到这样的实例,而杨辉三角则为我们开启了一扇透视高维空间的窗.将点、单位线段、单位正方形、单位正方体的所含点、线、面、体的个数做成下表(这里将点看作是0维的):

_维___ _数 顶点数_ _棱数_ _面数_ _三维面_ _四维面_ _五维面..._ ______ ____ 01____ ______ _______ _________ _________ ___________ ______ ____ 12___ ___1___ ______ _________ _________ ___________ ______ ____ 24___ ___4___ __1___ ________ _________ ____________ ______ ____ 38____ __12__ ___6__ ____1____ ________ ____________ ______ ___416___ __32__ __24__ ____8___ ____1____ ___________ ______ _________ _______ ______ _________ _________ ___________ _5 ...
可以发现,顶点数的规律是2k,棱数为低一维的顶点数加上低一维棱数的2倍,即4=2+1×2,12=4+4×2,32= 8+12×2.类比杨辉三角,写成下面的形式,规律就更明显了.

显然,这里有和杨辉三角类似的性质,下一行的数为它的左肩上的数与右肩上数的2倍之和,那么据此可以得出任意维“立方体”顶点数、棱数、面数、三维面、四维面等的个数了.
这里还有一个值得注意的有趣现象,即这里每一行的数均为(2x+1)n展开式中的各项系数.如当n=4时,对应的就是4维“立方体”,展开每一项系数分别为和上面第五行是完全对应的.由此,讨论高维空间中的点、线、面、体的个数问题就变得简单了.
3 自然数幂和问题
所谓自然数幂和问题,是指
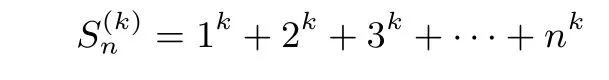
的求和问题.中学遇到的是k=1,2,3的三种情形,对于这三种比较简单的情形,方法比较多.波利亚的《数学的发现》一书中就给出了多种解法,文献[8]在《二次幂和十一法》一文中给出了二次幂和的十一种求法.这里,我们通过类比杨辉三角给出一种简便的方法.
另外,易得到以下结论:


同样的,
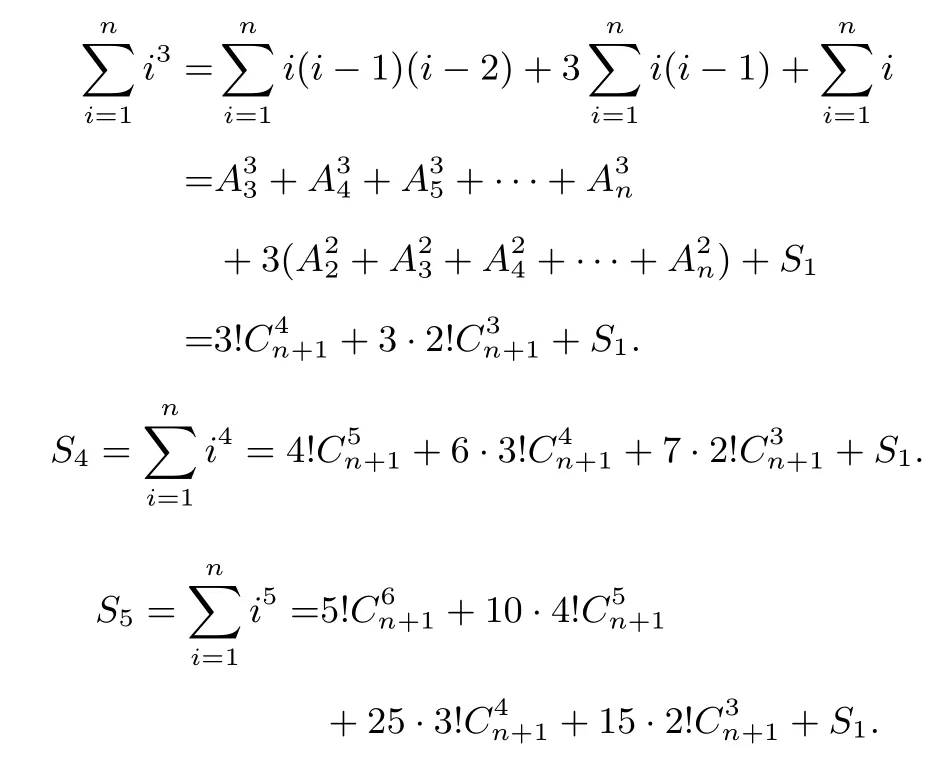
现在作一张“杨辉式”三角表,

斜着看,很容易发现,第二列下一个数,是其左肩上数的2倍与右肩的数之和;第三列下一个数是其左肩上数的3倍与右肩的数之和.这和杨辉三角的规律是类似的,以此类推.通过此表可以很容易的求出任意次幂的自然数和.
比如,我们可以容易的得到S7的表达式

综上,我们将运用类比的方法并结合杨辉三角比较简洁的解决了三个问题.管中窥豹,可以看出,类比法是一种非常适用而且有用的方法.“看起来类比推断是最普遍的推论方法,也许是最重要的一种”.数学问题解决过程中,在对命题的推广引申,类比思维具有不可忽视的重要作用.因此,教师在教学过程中,应该有意或无意的向学生“渗透”类比的思想.
很多时候,在解决一些题目时,我们总会想到以前成功解决的类似题目,这实际上就是一种类比.不仅如此,类比法还渗透到许多方面,在各种不同层次上得到运用.中国古代第一篇专门论述教育与教学问题的专著——《学记》,也提到“故君子之教,喻也.”这里的“喻”就是打比方、举例子,本质上就是一种类比.对于类比的重要性,开普勒的一句话是一个很好的评价,“我珍视类比胜于任何别的东西,它是我最可信赖的老师”.
从心理学的角度看,类比思维的核心是通过一个映射的过程,将知识从一种情境转化到另一种情境,在两种信息的主要方面找到一一对应的关系.并将已经得到解决的问题称为“源问题”(source problem),将待解决的问题称为“靶问题”(target problem).而类比就是要找到“源问题”和“靶问题”之间的关系,并将用于解决“源问题”的方法经过适当变化用于解决“靶问题”.
最后,需要强调的是,并不是任何时候的类比得到的结果都是正确的.类比推理得到的结论具有或然性.下面即是一例,级数

收敛,
现在

作简单变形,
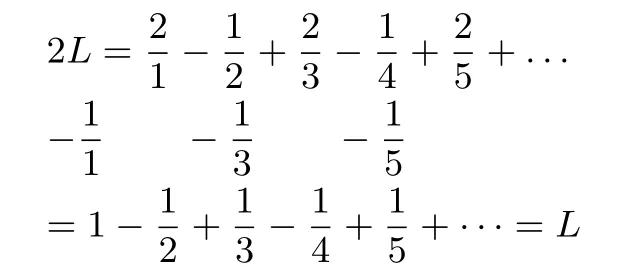
这里L显然是不为0的,但却得到了2L=L,错在哪里?
[1]李文林.数学史概论[M].北京:高等教育出版社,2011.
[2]王雄伟.杨辉三角数字排列的一些性质 [J].中学数学月刊, 2005(5):28-29.
[3]李国兴.杨辉三角的一个有趣性质[J].西北轻工业学院学报,2000, 18(2):107-108.
[4]胡恩良,朱维宗.杨辉三角形中的几条组合性质[J].云南民族学院学报(自然科学版),2002,11(3):132-135.
[5]刘天亮,张利民.杨辉三角形的若干性质[J].数学的实践与认识, 2007,37(1):116-120.
[6]G.波利亚.数学与猜想[M].北京:科学出版社,2001.
[7]G.波利亚.怎样解题[M].上海:上海科技教育出版社,2007.
[8]汪晓勤.二次幂和十一法[J].中学教研,2001(10):38-41.
