正弦调制多光束激光外差测量压电材料电致伸缩系数

2017-12-05甄佳奇仲维丹布音嘎日迪高亚臣王生钱李彦超

发光学报 2017年12期

关键词：外差电致玻璃板

甄佳奇，仲维丹，布音嘎日迪，高亚臣，刘勇，王生钱，李彦超

(黑龙江大学电子工程学院，黑龙江哈尔滨 150080)

正弦调制多光束激光外差测量压电材料电致伸缩系数

甄佳奇，仲维丹，布音嘎日迪，高亚臣，刘勇，王生钱，李彦超*

(黑龙江大学电子工程学院，黑龙江哈尔滨 150080)

电致伸缩系数反映了压电材料本身的固有属性，是衡量电致伸缩特性的重要参数之一。基于逆压电效应，准确测量微小长度变化量可实现电致伸缩系数的高精度测量。现有光学测量方法基于直接检测光强分布获取微小长度变化量，但受光源功率稳定性和环境扰动制约，测量精度不高。为此，本文采用多光束激光外差技术融合多普勒振镜正弦调制技术，加载微小长度变化量于外差信号频率中，研究测量微小长度变化量的外差信号理论模型及外差信号频率与电致伸缩系数间数学模型，实现外差信号频率检测取代直接强度检测，消除光源稳定性与环境扰动影响，并且采用频率解调可以同时获取多个微小长度变化量，对这些微小长度变化量加权平均，最终可以进一步提高电致伸缩系数的测量精度。以此为依据，通过理论仿真研究待测样品的电致伸缩系数，结果表明：该方法的相对测量误差仅为0.28%。与现有技术相比，测量精度提高了一个数量级。

电致伸缩系数；激光外差；正弦调制；多普勒效应；压电材料

1 引言

压电材料在涉及自动控制的机电系统和器件中具有重要应用，而电致伸缩系数反映了压电材料本身的固有属性，是衡量压电材料电致伸缩特性的重要参数之一，所以关于压电晶体材料电致伸缩特性的研究是国内外基础材料研究中的热门课题[1-6]。

基于逆压电效应，准确测量微小长度变化量可实现电致伸缩系数的高精度测量。目前，其测量方法主要有激光干涉法[7]、光杠杆法[8]、电容法[9]、电涡流法[10]和数字散斑相关法[11]等。但这些传统光学测量电致伸缩系数的方法是基于CCD相机的直接强度检测，通过测量光强分布获取待测信息。其局限性在于易受光源功率稳定性、环境扰动及CCD相机本身性能的影响，导致测量稳定性和精度不高，相对测量误差均高于1%，不能满足目前高精度测量的要求。

与之相比，激光外差测量技术[12-21]是目前普遍采用的高精度测量技术，具有空间和时间分辨率高、测量效率和精度高、线性度好、抗干扰能力强、动态响应快、重复性好、动态范围大及在线非接触测量等优点，已成为现代超精密检测及测量仪器的标志性技术之一。

值得注意的是，采用激光外差技术辅以光电探测器测量待测信息时，由于信号光和参考光的光频未发生变化，当信号光与参考光满足相干条件发生混频时，待测信息只调制在激光外差信号相位的变化上，属于零差测量技术，该技术利用相位解调获取待测信息，存在相位不易被探测、解调系统与算法复杂、系统稳定性差及效率低等缺点。

相对而言，激光外差信号频率解调获取待测信息可以采用快速傅里叶变换频谱分析方法实现，具有算法简单、容易实现及效率高等优点，能够克服相位解调存在的缺点，是目前激光外差测量领域研究的热点问题之一。将多普勒技术用于激光外差测量系统中，对不同时刻信号光和参考光进行频率调制，根据激光外差探测原理，可将微小长度变化量不仅加载于中频外差信号的相位中，也加载于频率中，弥补零差测量技术存在的不足，通过后续数字信号处理可实现频率解调获取微小长度变化量。

因此，本文首次将激光外差技术与多普勒技术深度融合，提出了一种高精度正弦调制多光束激光外差测量电致伸缩系数的新方法，即利用多普勒技术将微小长度变化量调制到外差信号频率中，通过对激光外差的解调可以精确获得微小长度变化量。本方法适用于任何压电材料电致伸缩系数的测量，本文以目前应用最广泛的PZT样品为例，仿真研究PZT的电致伸缩系数，结果表明相对测量误差为0.28%，同现有技术相比精度提高了一个量级。

2 测量原理

2.1电致伸缩系数测量原理

本文选用待测样品为一种圆管形压电陶瓷(PZT)，其外形和结构如图1所示。PZT圆管内外表面镀银作为电极，可以焊接引出导线后对其施外加电压。当在PZT外表面加正电压，内表面接地时，PZT伸长；反之，加负电压时，PZT缩短。

图1 圆管形压电陶瓷

圆管内外表面加电后，E为内外表面间形成的径向电场场强，ε为圆管轴向应变，α″为PZT准线性区的电致伸缩系数，则：

ε=α″E,

(1)

若加在PZT内外表面电压为U，PZT长度为l，Δl为加电后长度变化量，d′为圆管壁厚(均以mm为单位)，则有：

(2)

最终可得：

(3)

其中，U可由数字电压表读取，d′和l可用游标卡尺直接测得，当电压变化时，长度变化量Δl很小，无法用常规测量方法得到，因此需采用高精度方法测电致伸缩系数这个微小量[2-3]。

2.2多光束激光干涉原理

如图2所示，由于光线在薄玻璃板和平面反射镜2间不断反射与折射，反射光和透射光对无穷远处或者透镜焦平面上的干涉均有贡献，在研究这种干涉时，必须讨论多次反射与折射效应，即应研究多光束干涉。

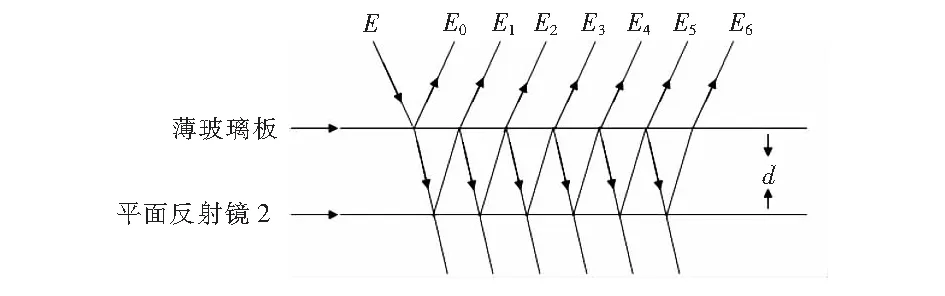
图2 多光束激光外差原理示意图

Fig.2Schematic diagram of linear frequency modulation multi-beam laser heterodyne

在不考虑薄玻璃板厚度条件下，激光斜入射至薄玻璃板时，设入射角为θ0，入射光场为E(t)=Elexp(iω0t)，多普勒振镜做简谐振动，其运动方程为x(t)=x0cos(ωct)，速度方程为v(t)=-ωcx0sin(ωct)。基于多普勒效应，反射光的频率变为ω=ω0(1-2ωcx0sin(ωct)/c)，c为光速，ω0为入射光场角频率，ωc为简谐振动角频率，x0为简谐振动振幅。则在t-l/c时刻，薄玻璃板前表面反射光为：

E0(t)=

αElexp{i[ω0(1-2ωcx0sin(ωc(t-l/c))/c)·

(t-l/c)+ω0x0cos(ωc(t-l/c))/c]}，

(4)

在不同时刻，透射薄玻璃板的光经平面反射镜多次反射，其各级反射光的表达式为：

(5)

其中，m为非负整数，l为振镜与薄玻璃板前表面之间距离，d为薄玻璃板与平面反射镜2之间距离，α与α1分别为薄玻璃板反射系数与透射系数，θ是折射角。

光电探测器接收总光场为：

E(t)=E0(t)+E1(t)+…+Em(t)+…，

(6)

根据光电转换原理，光电探测器输出光电流为：

(7)

其中，h为普朗克常数，η为量子效率，e为电子电量，ν为激光频率，Z是光电探测器表面介质本征阻抗，D是光电探测器光敏面面积。

式(7)中只考虑交流项，直流项经低通滤波器可被滤除，该交流项称为中频电流，用IIF表示：

Ej*(t)Ej+p(t))ds，

(8)

将式(4)和(5)代入式(8)，最终结果为：

(9)

式(9)忽略1/c3的小项后可简化为：

(10)

式中，p为非负整数。

由式(10)可知，中频电流的频率差及相位差都含距离d的信息。因为采用快速傅里叶变换(FFT)很容易实现频率解调而获取距离d，因此本文对频率差进行分析，用f表示中频信号频率成分，即为：

(11)

由式(11)可以看出，中频信号的频率与距离d成正比，且比例系数为：

(12)

n为薄玻璃板与平面反射镜2间的介质折射率，θ为折射角，ω0为激光角频率，简谐振动角频率ωc和振幅x0有关。

由式(9)和(10)还可以看出，光电探测器输出的中频电流包含许多谐波成分，各级谐波经FFT后可以得到各级谐波频谱，通过测量谐波频率，就可以得到薄玻璃板和平面反射镜2之间的距离d。当d改变时，就可以根据式(10)测出对应d的变化量Δd的数值，对Δd加权平均，就可以明显提高Δd的测量精度，Δd=Δl，知道了Δd就可以根据式(3)计算得到待测样品的电致伸缩系数。

3 光路设计

图3是基于正弦调制多光束激光外差测量压电材料电致伸缩系数的光路设计，该光路由激光器、平面反射镜1、偏振分束镜PBS、λ/4波片、多普勒振镜、薄玻璃板、会聚透镜、平面反射镜2、压电陶瓷管、二维调整架、高压电源、光电探测器、前置放大器、滤波器、A/D及DSP构成。多普勒振镜做简谐振动，其作用是对不同时刻入射光进行正弦频率调制。

图3 测量电致伸缩系数的光路设计

首先，打开激光器，使线偏振光分别经反射镜1、PBS和λ/4波片后入射至多普勒振镜前表面上，不同时刻被多普勒振镜正弦调制的反射光又经λ/4波片和PBS后斜入射至薄玻璃板上，经薄玻璃板透射的光被反射镜2反射后与薄玻璃板前表面反射光一起经会聚透镜会聚到光电探测器的光敏面上，最后光电流经前置放大器、A/D和DSP处理后可以获得不同时刻待测距离变化量的信息。

需要指出的是：用该装置进行测量时，应将贴有平面反射镜2的压电陶瓷管固定在二维调整架上，同时将薄玻璃板置于平面反射镜2前2cm处，利用二维调整架仔细调节使薄玻璃板和平面反射镜平行、等高，然后固定二维调整架即固定压电陶瓷管的一端使压电陶瓷管的长度只沿一个方向变化。利用高精度数字电压表监测输出电压值，读取并记录电压显示值U和信号处理后得到的Δl值。其中，Δl的大小恰好等于薄玻璃板和平面反射镜2之间距离的变化量Δd，就可以通过记录薄玻璃板和平面反射镜2之间距离的变化量Δd来获得Δl的数值。

4 仿真研究与结果分析

为验证正弦调制多光束激光外差法是否可行，基于图1所示光路，采用MATLAB软件模拟研究长为15mm、厚度为1.5mm的PZT材料电致伸缩系数，并取PZT材料电致伸缩系数理论值为1.85×10-9m/V。激光器波长λ为2050nm，薄玻璃板与平面反射镜之间介质折射率n取1，探测器灵敏度为1A/W，多普勒振镜的振幅为x0=0.001m。在仿真过程中，加在PZT上的电压的取值范围为0～800V，同时记录长度变化量的数值Δl。

如图4所示，为仿真得到的正弦调制多光束激光外差信号的FFT频谱，其中实线是斜入射时，测量长度变化量Δl对应的FFT频谱；虚线是激光正入射时，测量长度变化量Δl对应的FFT频谱。

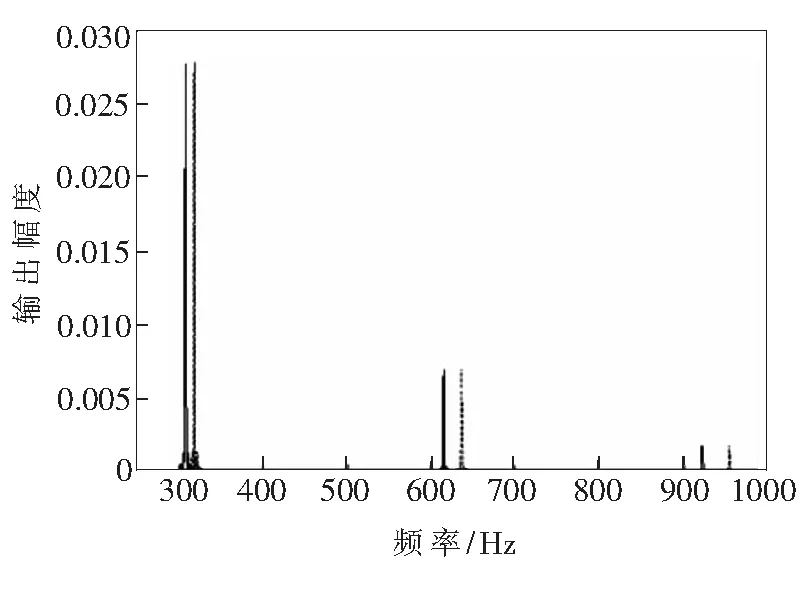
图4 多光束激光外差信号的频谱

Fig.4FFT spectrum of linear frequency modulation multi-beam laser heterodyne signal

由图4可见，正弦调制多光束激光外差信号频谱为等间隔分布，符合前面理论分析的结果。同时，还可以看出，仿真结果给出了正入射和斜入射情况下对应的频谱，根据图4可以得到正入射第一个主峰中心频率与斜入射第一个主峰中心频率的比值，即

ζ=cosθ，

(13)

因此，通过式(13)就可以得到折射角θ，基于斯涅耳定律可以得到入射角θ0，并通过式(12)可以获得Kp的数值，最终得到薄玻璃板和平面反射镜2之间距离变化量Δd的值。由于Δd=Δl，从而根据式(3)可以计算出任意入射角θ0情况下的PZT的电致伸缩系数。

如图5所示，仿真得到了不同电压条件下，测量PZT长度为变化量时对应的正弦调制多光束激光外差信号FFT频谱。由图5可知，随着电压U的增加，频谱向低频方向移动，即随着U的增加频率减小。原因在于：当电致伸缩系数不变时，电压和PZT长度变化量是成正比关系的，当电压增加时，PZT长度随之增加即薄玻璃板和平面反射镜2之间的距离随之减小，由于频率fp与平面反射镜2和透镜之间的距离d的关系为fp=Kpd，在Kp不变的情况下，频率fp和d呈线性光系，因此，平面反射镜2和薄玻璃板之间的距离d减小时，频率也随之减小，即随着U的增加，频谱向低频方向移动。

图5不同电压情况下，PZT长度变化量测量对应的频谱。

Fig.5Heterodyne signal spectrum of small length variation measurement under different voltage

表1不同电压条件下，PZT长度变化量Δl和对应电致伸缩系数α″的仿真测量结果

Tab.1 Simulation results of small length variation Δland the corresponding electrostriction coefficientsα″ under different voltage conditions

TimesV/VΔl/(10-6m)E/(10-9m·V-1)1100．01．8422911．8422912200．03．6845821．8422913300．05．5268711．8422904400．07．3691631．8422915500．09．2114551．8422916600．011．0537451．8422917700．012．9697041．8528158800．014．8119931．851499

在理论推导过程中，忽略了薄玻璃板的厚度即不考虑器件后表面的反射光对外差信号的影响，但实际上薄玻璃板的厚度是存在的，一般小于1 mm。为克服这种影响，根据式(11)，薄玻璃板后表面的反射光产生的多光束外差信号的频率分布在频谱的零频附近，在光路中加入滤波器就可以滤除低频外差信号的干扰。利用该方法，连续模拟8组数据，结果如表1所示。

需要说明的是：利用表1的仿真实验数据，根据式(3)可以计算出PZT的电致伸缩系数的平均测量值为1.844757×10-9m/V，这样就可以得到测量相对误差最大为0.28%。该方法明显提高了电致伸缩系数的测量精度。分析数据可知，仿真实验中误差来源于计算过程中的舍入误差及FFT后的精度误差。

5 结论

本文将多普勒振镜引到光路中，基于多普勒效应对不同时刻入射光进行正弦频率调制，这样经过薄玻璃板的反射光和平面反射镜多次反射的光在满足干涉的条件下，产生多光束外差信号，从而将待测信息成功地调制在中频外差信号的频率差中。在研究样品电致伸缩系数过程中，该方法在频域同时得到了包含距离变化量信息的多个频率值，信号解调后得到多个距离变化量，通过加权平均可以精确获得距离变化量。以PZT材料为例进行仿真实验研究，电致伸缩系数测量的相对误差仅为0.28%，显著提高了测量精度。

与其他测量方法相比，该方法具有光路结构简单、功耗小、操作方便、测量结果误差小、精度高等多方面优势，可以在精密测量领域中广泛使用。

[1] NADEZHDA A, LEONARD M S. Measurement of the electrostriction coefficient in liquids by stimulated Mandelshtam-Brillouin light scattering [J].SPIE, 2001, 4605:394-398.

[2] KHOLKIN A L, AKDOGAN E K, SAFARI A,etal.. Characterization of the effective electrostriction coefficients in ferroelectric thin films [J].J.Appl.Phys., 2001, 89(12):8066-8073.

[3] YURI M S, DANIEL J K. Material parameters for electrostriction [J].J.Appl.Phys., 1996, 80(8):4566-4572.

[4] LIU A C, DIGONNET MICHEL J F, KINO GORDON S. Measurement of the dc Kerr and electrostrictive phase modulation in silica [J].JOSAB, 2001, 18(2):187-194.

[5] LAM K S, ZHOU Y, WONG Y W,etal.. Electrostriction of lead zirconate titanate/polyurethane composites [J].J.Appl.Phys., 2005, 97(10):104112-104117.

[6] MUNN R W. Theory of piezoelectricity, electrostriction, and pyroelectricity in molecular crystals [J].J.Chem.Phys., 2010, 132(10):104512-104517.

[7] LIN R R. Measuring the coefficient of electrostriction with the method of laser interference [J].Phys.Experiment., 2009, 29(6):4-7.

[8] WU J F, LI J Q, LIN B P. Research of optical lever measure method on electrostrictive material strain [J].Meas.ControlTechnol., 2007, 26(11):68-70.

[9] WU J F, LI J Q, SONG A G,etal.. Electrostrictive material characteristic testing device based on capacitance method [J].Instrum.Tech.Sens., 2008(3):85-87.

[10] GAO J, GAO X X, LAN Y H. Measuring of magnetostriction using a noncontact electric eddy current sensor [J].J.Magnet.Mater.Dev., 2007(3):57-59.

[11] CHEN F X, CONG Y Q, LIN B P,etal.. Application of digital speckle correlation method for measuring electrostrictive effect [J].Instrum.Tech.Sens., 2006(6):52-54.

[12] JURNA M, KORTERIK J P, OTTO C,etal.. Shot noise limited heterodyne detection of CARS signals [J].Opt.Express, 2007, 15:15207-15213.

[13] CHEN K H, CHANG W Y, CHEN J H. Measurement of the pretilt angle and the cell gap of nematic liquid crystal cells by heterodyne interferometry [J].Opt.Express, 2009, 17:14143-14149.

[14] HIRAI A, MATSUMOTO H, LIN D,etal.. Heterodyne Fourier transform spectrometer for the near-infrared region [J].Opt.Express, 2003, 11:1258-1264.

[15] BITOU Y. Phase-shifting interferometry with feedback control using heterodyne phase detection [J].Opt.Lett., 2008, 33:1777-1779.

[16] 宋晨, 吕岑, 郭琪，等. 一种激光外差多普勒玻璃厚度测量方法 [J]. 光子学报, 2008, 37(8):1635-1638.

SONG C, LYU C, GUO Q,etal.. One method for measuring thickness of glass by using laser heterodyne and Doppler [J].ActaPhoton.Sinica, 2008, 37(8):1635-1638. (in Chinese)

[17] 庞亚军, 王春晖, 唐甜甜. 双平衡式相干接收原理及其在外差干涉仪中的应用研究 [J]. 光子学报, 2012, 41(9): 1015-1018.

PANG Y J, WANG C H, TANG T T. Principle of dual-balanced coherent receive and its application in heterodyne interferometer [J].ActaPhoton.Sinica, 2012, 41(9):1015-1018. (in Chinese)

[18] 李晴棉, 李也凡, 何大伟, 等. 光外差电信号接收机 [J]. 发光学报, 1998, 19(1):82-84.

LI Q M, LI Y F, HE D W,etal.. Optics heterodyneing electronic signals receiving device [J].Chin.J.Lumin., 1998, 19(1):82-84. (in Chinese)

[19] 梁赫西, 代永红, 艾勇, 等. 本振功率对空间平衡探测器相干探测灵敏度的影响 [J]. 光学精密工程, 2017, 25(2):334-341.

LIANG H X, DAI Y H, AI Y,etal.. Influence of local oscillator power on sensitivity of coherent detection of space balance detector [J].Opt.PrecisionEng., 2017, 25(2):334-341. (in Chinese)

[20] 钟金钢, 梁智强, 李仕萍. 激光自混合干涉角度测量参数优化及旋转方向判别[J]. 光学精密工程, 2016, 24(5):1001-1008.

ZHONG J G, LAING Z Q, LI S P. Parameter optimization and direction recognition in ankle measurement by laser self-mixing interference [J].Opt.PrecisionEng., 2016, 24(5):1001-1008. (in Chinese)

[21] 刘丁枭, 盛伟繁, 王秋实, 等. 拼接干涉技术在同步辐射领域的发展现状及趋势 [J]. 光学精密工程, 2016, 24(10):2354-2366.

LIU D X, SHENG W F, WANG Q S,etal.. Current status and trends of stitching interferometry in synchrotron radiation field [J].Opt.PrecisionEng., 2016, 24(10):2354-2366. (in Chinese)

PiezoelectricMaterialElectrostrictionCoefficientMeasurementMethodCombinedSinusoidalModulationwithMulti-beamLaserHeterodyne

ZHENJia-qi,ZHONGWei-dan,BUYingaridi,GAOYa-chen,LIUYong,WANGSheng-qian,LIYan-chao*

(ElectronicEngineeringCollege,HeilongjiangUniversity,Harbin150080,China)

The electrostriction coefficient can be accurately measured by using small length variation based on inverse piezoelectric effect. The conventional optical measuring method based on direct detection of light intensity distribution to obtain small length variation is restricted by light source power stability and environmental perturbation, and can not reach high measuring accuracy. This paper uses the combination of multi-beam laser heterodyne technique with sinusoidal modulation technique to load small length variation to the heterodyne signal frequency. By researching on the theoretical models of heterodyne signal for measuring small length variation, and the relationship between heterodyne signal frequency and electrostriction coefficient, the direct intensity detection can be replaced by heterodyne signal frequency detection, the effects of light source power stability and environmental perturbation can be removed. Many values of small length variation can be got by using the frequency demodulation simultaneously. Processing these values by weighted-average, can get length variation accurately, and eventually get value of electrostriction coefficient of piezoelectric material by the calculation. The measuring accuracy of electrostriction coefficient can be further improved. Based on this, the theoretical simulation research on electrostriction coefficient of testing sample can be acted, the obtained results show that the relative measurement error of this method is just0.28%. The measuring accuracy is improved one order of magnitude compared with existing technique.

electrostriction coefficient; laser heterodyne; sinusoidal modulation; Doppler effect; piezoelectric material

2017-04-26；

2017-06-03

国家自然科学基金(61505050，61501176)；黑龙江省自然科学基金(F2015015)；黑龙江大学杰出青年科学基金(JCL201504)；中国博士后科学基金(2014M561381)；黑龙江省博士后科学基金(LBH-Z14178)；黑龙江省高校大学专项科研资金(HDRCCX-2016Z10); 大学生创新创业训练项目(201710212101)；黑龙江大学新世纪教育教学改革(创新创业教育专项)(2017CCY007)资助项目

Supported by National Natural Science Foundation of China(61505050,61501176); Natural Science Foundation of Heilongjiang Province(F2015015); Outstanding Young Scientist Foundation of Heilongjiang University(JCL201504); China Postdoctoral Science Foundation(2014M561381); Postdoctoral Foundation of Heilongjiang Province(LBH-Z14178); Special Research Funds for The Universities of Heilongjiang Province(HDRCCX-2016Z10); Innovative Entrepreneurship Training Program for Undergraduates(201710212101); Heilongjiang University New Century Education Teaching Reform Project (Innovation and Entrepreneurship Education)(2017CCY007)

1000-7032(2017)12-1661-07

NO32

10.3788/fgxb20173812.1661

*CorrespondingAuthor,E-mail:ycl.hit1982@aliyun.com