剖析平面向量求解中的八种错误

■江苏省高港中等专业学校 李 霖

平面向量融数、形于一体,具有几何与代数的“双重身份”,它是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景,它包括向量的概念和运算。本文汇集了同学们在求解向量问题中的种种错误,展示剖析其原因,攻克易错点,给出提醒,希望对同学们的复习能有所帮助。

错误1——忽视向量概念中的特殊情况

四个命题:(1)0·a=0;(2)0·a=0;(3)0-;(4)a·b =a ·b。其中正确的个数为( )。

A.1 B.2

C.3 D.4

错解:全都正确,选D。

剖析:(1)根据向量数量积的概念,0·a应是一个实数0,而非一个向量,正确;(2)根据实数与向量的定义,0·a应是一个向量,而非一个实数,错误;(3)由向量的减法运算和共线的意义,正确;(4)根据数量积的定义a·b =a ·b cosθ,原式只有当θ=0或π时成立,错误。由以上分析可知,正确答案为B。

提醒:向量的有关概念的判断中一定要注意定义的本质属性,区分特殊的情况和一般成立的关系,注意零向量和实数零的区别。

变式1 以下命题正确的是( )。

Aa.∥b,b∥c⇒a∥c

B.若a与b互为相反向量,则a+b=0

C.平面向量a,b平行的充要条件是存在不全为0的实数λ1,λ2,使得λ1a+λ2b=0

D.若a与b互为相反向量,则a≠b

解析:当b=0时,A中结论错误;互为相反向量的和为零向量0而不是实数0,B中结论错误;当a=0时,其相反向量也是0,此时a=b,D中结论错误;只有C正确。

错误2——忽视平面向量基本定理的成立条件

下列各组向量中,可以作为基底的是( )。

A.a=(0,0),b=(1,-2)

B.a=(-1,2),b=(5,7)

C.a=(3,5),b=(6,10)

D.a=(2,-3),b=(4,-6)

错解:选A或C或D。

剖析:根据基底的定义,只有非零且不共线的向量才可以作为平面内的基底。一一验证非零不共线的向量只有B。

提醒:如果a、b是同一平面内的两个不共线向量,那么对该平面内的任一向量c,有且只有一对实数λ1,λ2,使c=λ1a+λ2b。解决问题的一般思路是:先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决。

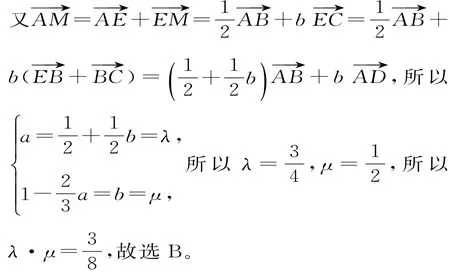
错误3——弄错一个向量在另一个向量上的正投影

错误4——忽视向量数量积与实数乘法的区别

已知a、b都是非零向量,且向量a+3b与7a-5b垂直,向量a-4b与7a-2b垂直,求向量a与b的夹角。

错解:由题意可得:

两式相减得46a·b-23b2=0,即b(2a-b)=0,所以b=0(不合题意舍去)或2ab=0,由2a-b=0知a与b同向,故向量a与b的夹角为0°。

剖析:本题误用实数的性质,即实数a、b若满足ab=0则必有a=0或b=0,但对于向量a、b若满足a·b=0,则不一定有a=0或b=0,因为由a·b=|a|·|b|cosθ知与θ有关,当θ=90°时,a·b=0恒成立,此时a、b均可以不为0。

由错解知b2=2a·b,代入7a2+16a·b-15b2=0,得a2=2a·b,所以a2=b2=

提醒:数量积的运算不满足结合律也不满足消去律,平面向量投影问题的易错点是:①忽视“哪个向量”在“另一个向量”上的投影;② 要注意投影是一个数量,不是向量,其值可正,可负,可为0。

变式4 已知命题:(1)(a ·b)·c=a·(b ·c);(2)a+b ≤a +b ;(3)(a -b)·c=a·c-b·c;(4)如果a·b=a·c,且a=0,那么b,c在a方向上的投影相等。其中正确的个数是( )。

A.1 B.2 C.3 D.4

解析:(1)数量积的运算不满足结合律,不能与实数运算混淆,错误。(2)由向量几何运算的意义及平行四边形法则可知正确。(3)结合向量的运算法则可知正确。(4)a·b=a·c,说明b,c在a方向上的投影相等,正确。

错误5——忽略共线向量或三点共线的条件

已知同一平面上的向量a、b、c两两所成的角相等,并且|a|=1,|b|=2,|c|=3,求向量a+b+c的长度。

错解:易知a、b、c皆为非零向量,设a、b、c所成的角均为θ,则3θ=360°,即θ=120°,所以a·b=|a|·|b|cos120°=-1,同理b·c=-3,c·a=-,由|a+b+c|2=a2+b2+c2+2a·b+2b·c+2c·a=3,得|a+b+c|=3。

剖析:错解以为a、b、c皆为非共线向量,而当向量a、b、c共线且同向时,所成的角也相等均为0°,符合题意。(1)当向量a、b、c共线且同向时,所成的角均为0°,所以|a+b+c|=|a|+|b|+|c|=6;(2)当向量a、b、c不共线时,同错解。

综上所述,向量的长度为6或3。

变式5 如图1,在△ABC中,AD=DB,AE=EC,CD与BE交于点F,设=xa+yb,则(x,y)为( )。

图1

错误6——忽略向量的几何意义与三角形“内心”之间的关系

A.外心 B.内心 C.重心 D.垂心

错解:选A、C或D。

变式6 已知△ABC的三内角A,B,C所对边的长依次为a,b,c,M为该三角形所在平面内的一点,若a0,则M是△ABC的( )。

图2

A.内心 B.重心 C.垂心 D.外心平分线。同理可证AM、BM的延长线也是角平分线。故M是△ABC的内心。

错误7——忽略向量的几何意义与三角形“垂心”之间的关系

已知O是平面上的一定点,A、B、C是平面上不共线的三个点,动点P满足λ∈[0,+∞),则动点P的轨迹一定通过△ABC的( )。

A.重心 B.垂心 C.外心 D.内心

错解:选A、C或D。

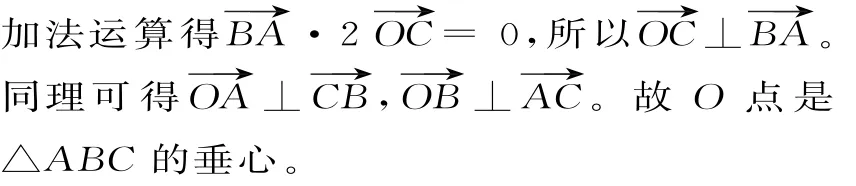
错误8——忽略向量的几何意义与三角形“重心”之间的关系

A.重心 B.垂心 C.外心 D.内心

错解:选B、C或D。