一道向量问题的多角度探究

■河南师范大学附属中学 刘长杰

编者的话:“经典题突破方法”栏目里例、习题选名校模拟题或三年高考真题,推出本栏目的主要目的是让同学们更好地领悟数学解题思想方法,通过多解多变培养同学们多思多想的好习惯。学会解题反思,无疑是同学们学习的一条捷径,愿同学们不断在反思中进步,在反思中收获!

学习数学离不开解题,解题时要善于从多角度审视和分析问题,不断开发解题潜能,进而提高解决综合问题的能力。下面是一道平面向量的数量积的综合问题,笔者变换角度给出三种解法,供同学们学习时参考。

【考点定位】本题是平面向量问题,考查学生对于平面向量数量积知识的理解。其中包含动点问题,考查同学们对最值求法的掌握情况。

【考查意图】本题考查平面向量的线性运算、数量积运算等基础知识,考查数形结合思想,考查运算求解能力。

分析1:利用一组基底表示所有向量,利用向量数量积的定义来计算。

分析2:建立平面直角坐标系,利用坐标研究向量的数量积。

解法2:如图2所示,以点D为坐标原点,直线DC,DA分别为x轴,y轴,建立平

【名师点睛】对向量的数量积问题,我们常采用三种处理方法:

(1)向量运算。选择一组基底,用向量的线性运算表示所有向量;再利用向量数量积的定义来计算。这种方法技巧性较强,并且有时运算量较大。

(2)坐标运算。把向量的运算转化为坐标运算,即向量问题代数化。这需要建立恰当的坐标系,并且要有一定的代数变形能力。

(3)几何运算。根据向量的几何意义,把向量的运算结果转化为几何图形的特征,即向量问题图形化。这种方法综合性较强。

【复习建议】一道向量问题,通过多角度的认识,使思维的方法与知识的应用各不相同。一题多思,有益于知识的对比,更有利于思维批判性的养成。在平时的复习备考中,同学们要加强这方面的训练。

跟踪练习:如图4所示,圆O的半径为3,单位向量e所在的直线与圆相切于点A,B是圆上的动点,则e·的最大值为____。

【审题方法】此问题是向量数量积的综合应用,可以采用例题的解法来尝试解决。

【解题思路】利用向量数量积的定义结合三角变换来计算,也可把向量的运算转化为坐标运算,还可以利用投影来计算。

图4

图5

解法2:如图6所示,以O为坐标原点,直线OA为x轴,过点O且与直线OA垂直的直线为y轴,建立平面直角坐标系,则A(3,0)。设B(x,y)(-3≤x≤3,-3≤y≤3),则=(x-3,y)。设e,由e =1,知 D(3,1),则=(0,1)。所以=0×(x-3)+1×y=y≤3,即的最大值为3。

图6

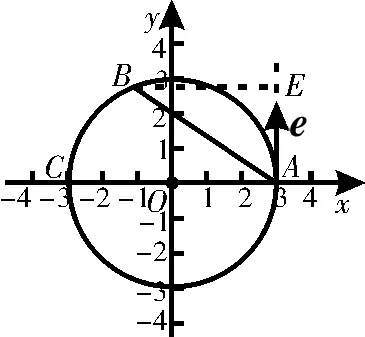
图7

高考数学试题愈来愈注重对学生综合能力的考查。在学习中有意识地进行一题多解的训练,会不断优化同学们的思维品质,培养同学们的发散思维,提高同学们的创新能力,促进知识的融会贯通。在平时的学习过程中,大家一定要加强这方面的训练,从而提升自身的数学素养与解题水平。